矩形6.1(3)

(共13张PPT)
温故而知
赠言：
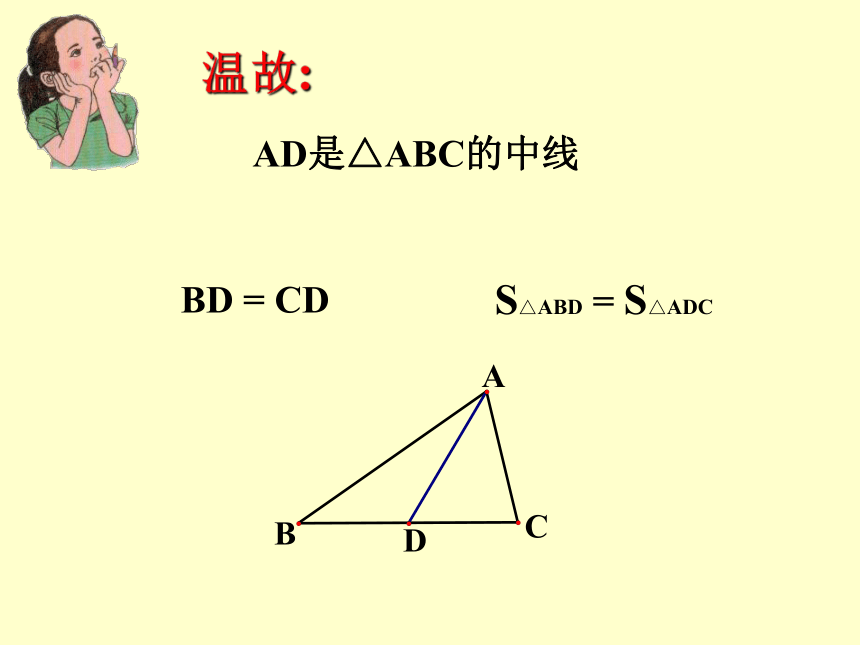
AD是△ABC的中线
BD = CD
S△ABD = S△ADC
A
D
B
C
温故:
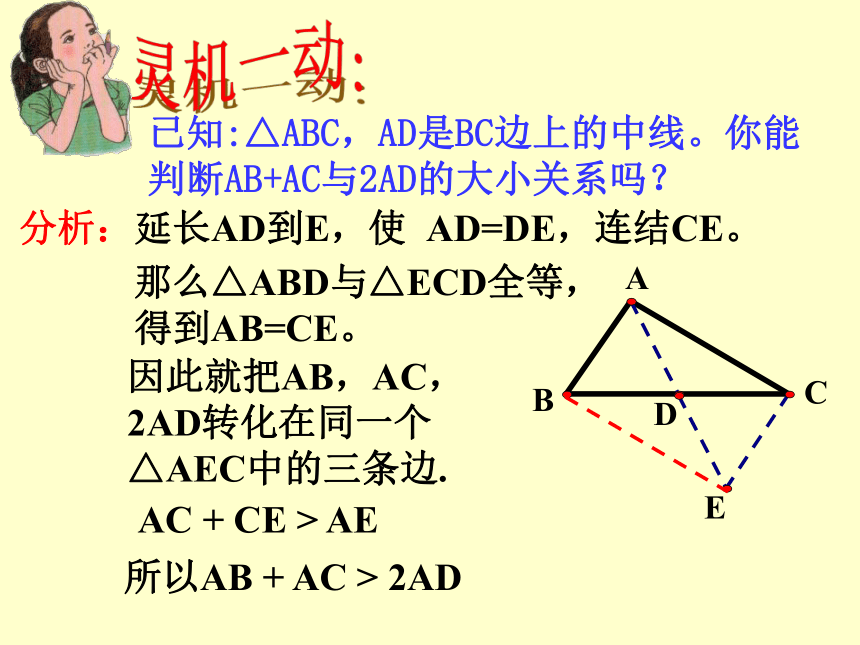
已知:△ABC，AD是BC边上的中线。你能判断AB+AC与2AD的大小关系吗？
A
B
C
D
E
分析：延长AD到E，使 AD=DE，连结CE。
那么△ABD与△ECD全等，得到AB=CE。
因此就把AB，AC，2AD转化在同一个△AEC中的三条边.
AC + CE > AE
所以AB + AC > 2AD
模仿秀:
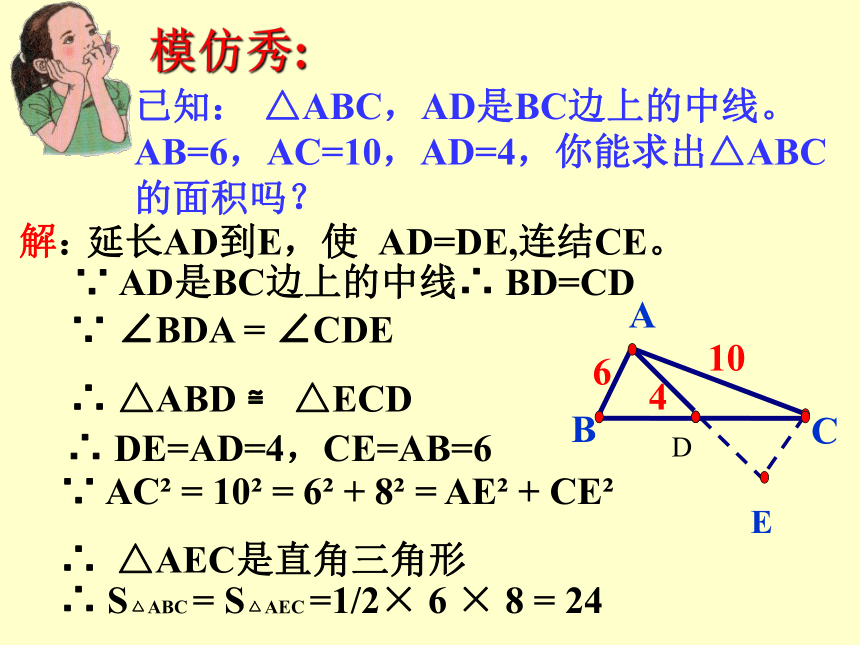
已知： △ABC，AD是BC边上的中线。 AB=6，AC=10，AD=4，你能求出△ABC的面积吗？
A
B
D
E
C
6
10
4
解：
延长AD到E，使 AD=DE,连结CE。
∵ AD是BC边上的中线∴ BD=CD
∵ ∠BDA = ∠CDE
∴ △ABD ≌ △ECD
∴ DE=AD=4，CE=AB=6
∵ AC = 10 = 6 + 8 = AE + CE
∴ △AEC是直角三角形
∴ S ABC = S AEC =1/2× 6 × 8 = 24
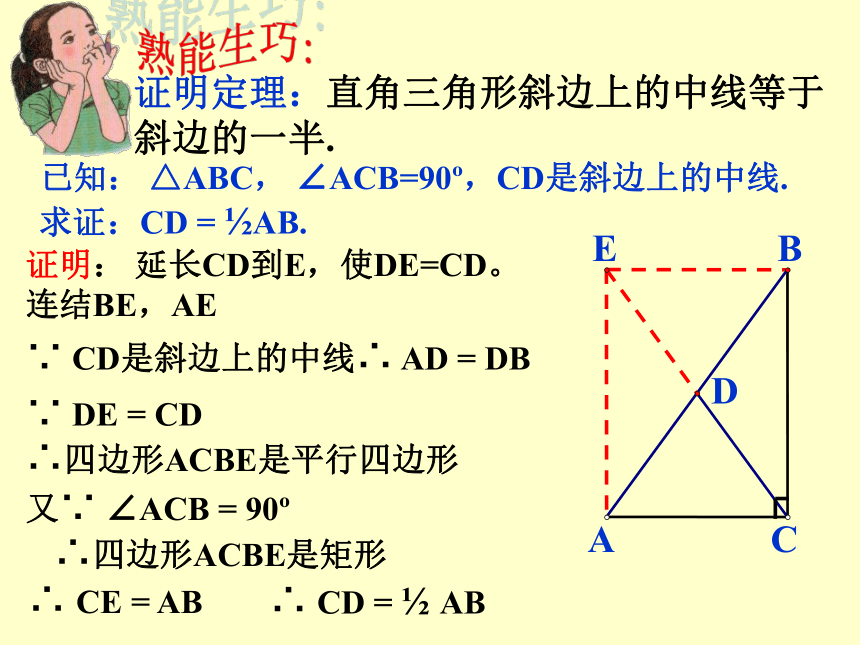
证明定理：直角三角形斜边上的中线等于
斜边的一半.
已知： △ABC， ∠ACB=90 ，CD是斜边上的中线.
求证：CD = AB.
A
B
C
D
E
证明： 延长CD到E，使DE=CD。连结BE，AE
∵ CD是斜边上的中线∴ AD = DB
∵ DE = CD
∴四边形ACBE是平行四边形
又∵ ∠ACB = 90
∴四边形ACBE是矩形
∴ CE = AB
∴ CD = AB
例1、如图，已知AD⊥BD，AC⊥BC，E为AB的中点，试判断DE与CE是否相等，并说明理由。
变式题：如图，已知AD、BE分别是△ABC的BC、AC边上的高，F是DE的中点，G是AB的中点，则FG⊥DE，请说明理由。
已知：在矩形ABCD中，AB = 8，BC = 10，折叠矩形的一边AD，使点D落在BC边的点F处，折痕为AE，求CE的长？
A
B
C
D
E
F
分析： 这是 关于折叠问题
实质是轴对称问题
△AFE ≌ △ADE
AF=AD=BC=10
EF=DE
BF=6
AB=8
CD=AB=8
EF=8 – CE
CF=4
BC=10
（8–CE） = 4 + CE
已知：矩形ABCD，AB = 6，BC = 8。沿对角线BD对折后，与AD相交与点E。
求△BDE的面积.
A
B
C
D
E
C
6
8
分析：
2.你觉得△BC D ≌ △BCD，哪些最有助于我们解决问题？
1.求面积你觉得哪条为底好？
3.令DE = X
则X = 6 +（8 – X）
（ ∠ C BD = ∠CBD）
温故：
知型：
学习要温故，但也要注意型。任何事物都是型中有异，异中有型。只有这样，学习才能学活。而不是简单地一招一式。
三角形的中线及应用.
直角三角形斜边上的中线等于斜边的一半.
矩形的性质与判定.
温故而知型
你说我说大家说
请你谈谈学习本节课后的感受!