6.2菱形1

(共20张PPT)
生活是数学的源泉,
探索是数学的生命线!
------高 斯
高斯：（1777年4月30日—1855年2月 ）
德国著名数学家、物理学家、天文学家、大地测量学家。
他有数学王子的美誉，并被誉为历史上最伟大的数学家之一，
和阿基米德、牛顿、欧拉同享盛名。
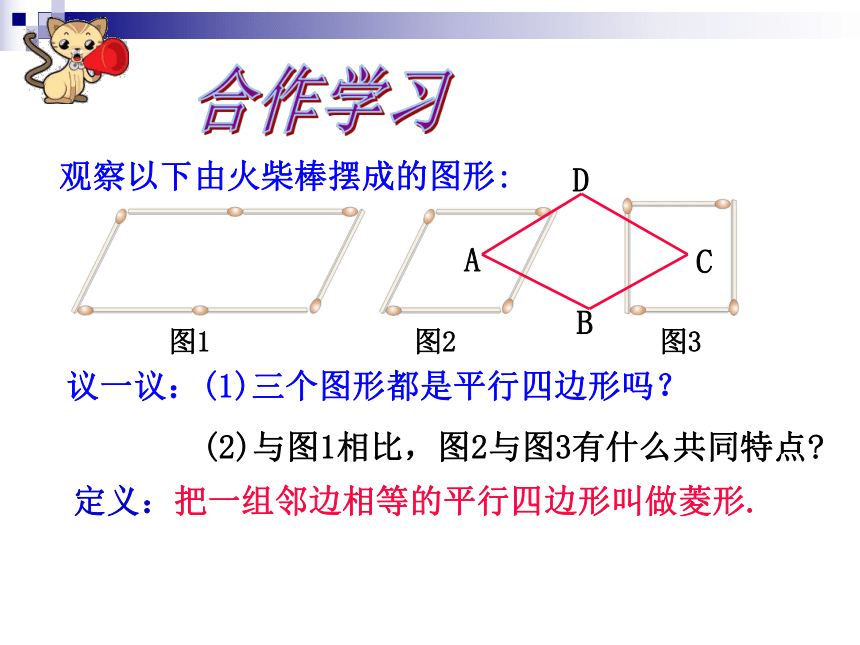
观察以下由火柴棒摆成的图形:
议一议：(1)三个图形都是平行四边形吗？
(2)与图1相比，图2与图3有什么共同特点
定义：把一组邻边相等的平行四边形叫做菱形.
A
B
C
D
图1 图2 图3
菱形是特殊的平行四边形，具有
一般平行四边形的一切性质.
A
B
C
D
一、两组对边分别平行
二、两组对边分别相等
三、对角相等、邻角互补
四、两条对角线互相平分
特殊性质：（菱形具有，而一般平行四边形不具有的性质。）
菱形的性质1：菱形的四条边都相等。
菱形的性质2：菱形的两条对角线互相垂直，
每一条对角线平分一组对角。
从边来看：
从对角线来看：
A
B
C
D
O
请同学们思考定理2的证明
已知:四边形ABCD是菱形 , 对角线AC,BD交于点O.
求证: AC⊥BD,AC平分∠BAD和∠BCD. BD平分∠ABC和∠ADC
A
B
C
D
O
由定理2可以得出,菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴.
定理2.菱形的对角线互相垂直, 并且每条对角线平分一组对角.
定理1.菱形的四条边都相等.
已知菱形的周长是16cm，则菱形的边长是________cm
4
如图，在菱形ABCD中，∠ABD=400 ， 则∠ABC= 度
80
)
400
在菱形ABCD中，对角线AC与BD相交于点O，已知AO=3，BO=4，则AB=
5
菱形的两条对角线分别是8和6,则菱形的面积是
24
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
A
B
C
D
O
你能求出这个菱形的面积吗？
面积：S菱形=对角线乘积的一半
数学思想:将菱形转化为三角形的思想
1.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F.求证:AE=AF.
变式1：已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F,且E,F分别是BC,CD的中点,求∠EAF的度数.
A
B
C
D
E
F
已知:在菱形ABCD中, ∠BAD=1200 ,E,F是线段BC,CD上的动点, 在运动过程中,始终保持∠EAF=600, 那么BE+DF与AB有着怎样的数量关系
点拨:在菱形中,如果有600的内角,通常采取连接对角线构造等边三角形.
一组邻边相等的平行四边形叫做菱形.
定理1.菱形的四条边都相等.
定理2.菱形的对角线相互垂直,
并且每条对角线平分一组对角
菱形是轴对称图形,它的两条对角线所在的直线
都是它的对称轴.
面积：S菱形=对角线乘积的一半
1.转化的数学思想
知识体系:
思想方法:
2. 构造等边三角形
菱形ABCD,∠ABC=60°,AB=4cm,P为BD上任意一点,E为BC中点,求PE+PC的最小值.
B
C
D
E
P
A