浙教版七上数学第三章 实数复习课件(24张ppt)
文档属性
| 名称 | 浙教版七上数学第三章 实数复习课件(24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-02 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
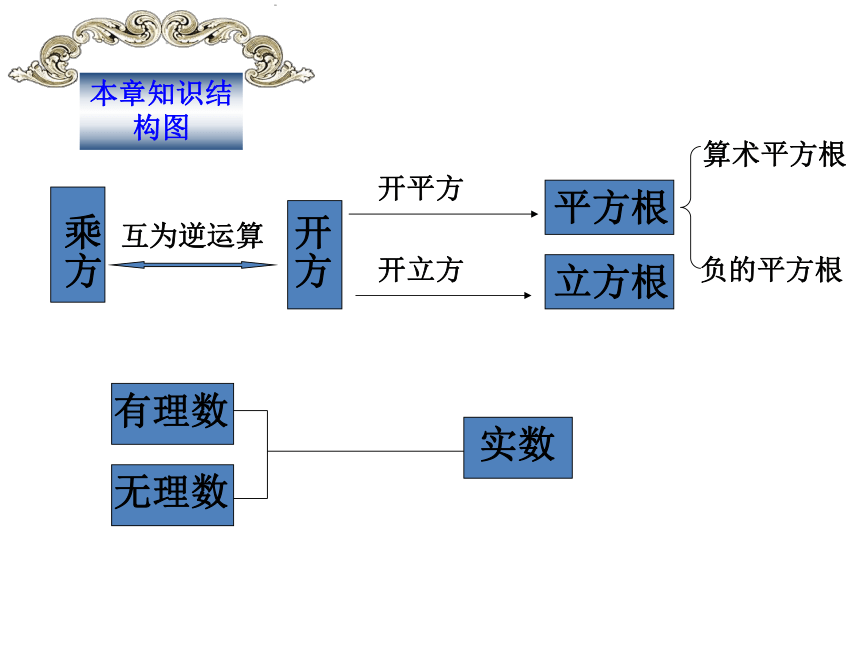
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
1.算术平方根的定义:
特殊:0的算术平方根是0。
一般地,如果一个数的平方等于a
,那么这个数就叫做a
的平方根(或二次方根).
这就是说,如果x
2
=
a
,那么
x
就叫做
a
的平方根.a的平方根记为±
2.
平方根的定义:
3.平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
4.立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作
.
5.立方根的性质:
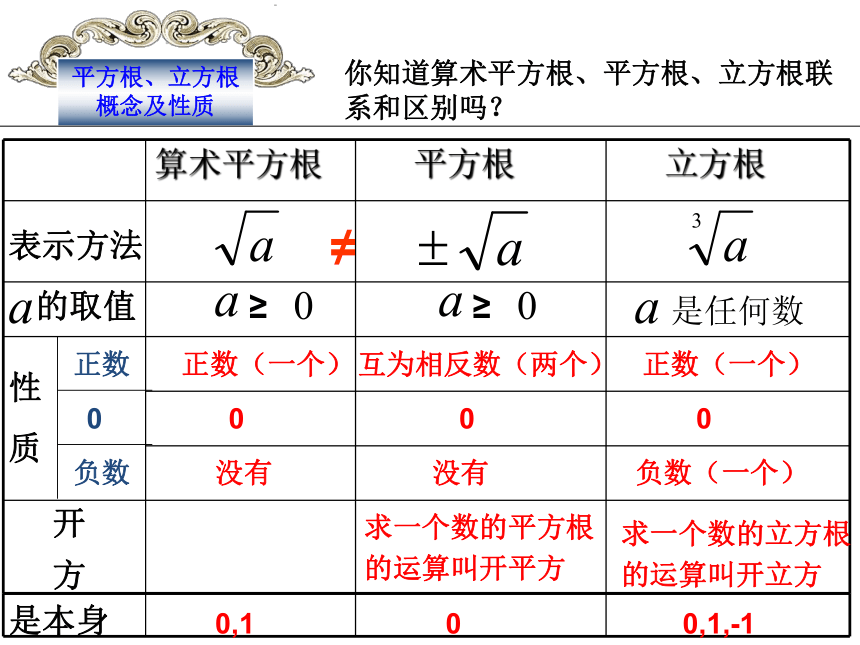
平方根、立方根概念及性质
你知道算术平方根、平方根、立方根联系和区别吗?
表示方法
性
质
开
方
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
算术平方根
平方根
立方根
1.求下列各数的算术平方根:
(1)
0.04;
(2)
1;
(3)
(-3)2
;
(4)
3.求下列各数的立方根:
(1)
121;(2)
16;
(3)
0
;
(4)
(-3)2
;
(5)
2.求下列各数的平方根:
(1)
-0.008;(2)
43;
(3)
-64;
(4)
(-3)3;
(5)
4.求下列各式的值:
求根也好,求值也好,关键要弄清它是什么意思,然后可以选择定义和性质来求.
不要搞错了
64
±8
8
-4
___.
-4,-3,-2,-1,
0,1,2,3
一、平方根和立方根
1.
16的平方根是_____,符号表示为_____;
16的算术平方根是____,符号表示为_____.
2.
27的立方根是____,符号表示为_____.
3.下列数中的无理数是______________
-1,
,0.3,
,
0
,
0.101
001
000
1…(相邻两个1之间0的个数逐次加1).
3
4
0.101
001
000
1…
=
2
=2
利用定义
无理数也有乘除运算,在后面的章节里将会学习,也满足先定符号,再计算.
三、实数的运算
不要遗漏哦!
解下列方程:
当方程中出现平方时,若有解,一般都有两个解
当方程中出现立方时,一般都有一个解
1.
解:
2.
解:
掌握规律
注意平方根和立方根的移位法则
1、无限不循环的小数
叫做无理数.
有理数和无理数统称实数.
3、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
5、在进行实数的运算时,有理数的运算法则及运算性质同样适用。
2、实数与数轴上的点是一一对应的.
4、实数的大小比较方法有:利用数轴比较、利用绝对值比较、求平方比较、求差比较、求商比较和计算近似值比较等方法。
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1、判断下列说法是否正确:
1.实数不是有理数就是无理数。
(
)
2.无限小数都是无理数。
(
)
3.无理数都是无限小数。
(
)
4.带根号的数都是无理数。
(
)
5.两个无理数之积一定是无理数。(
)
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。(
)
有理数集合:{
};
1、把下列各数填在相应的大括号内:
整数集合:{
……};
奇数集合:{
……};
无理数集合:{
}。
-1
π,
2.1010010001…
2、把下列各数分别填入相应的集合内:
有理数集合
无理数集合
是负数
等于它的相反数
是正数
等于它本身
是负数
里面的数的符号
化简绝对值要看它
等于它的相反数
要学会计算哟!
计算:
3、已知
位置如图所示,
试化简
解:原式=-a-(b-a)+(c-a)-(c-b)
=-a-b+a+c-a-c+b=-a
解:原式=-(a+b-c)+(-b+2c)+(b-a)
=-a-b+c-b+2c+b-a
=-2a-b+3c
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
例题;求下列各数的相反数和绝对值
解:
相反数
绝对值
1、正实数的绝对值是
,0的绝对值是
,负实数的绝对值是
.
它本身
0
它的相反数
5、判断
(1)带根号的数都是无理数。
(2)无理数就是开方开不尽的数。
(3)有限小数是有理数,无限小数是无理数。
6、实数
在数轴上对应的点的位置关系如图所示,下列式子错误的是(
)
×
×
×
C
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
1.算术平方根的定义:
特殊:0的算术平方根是0。
一般地,如果一个数的平方等于a
,那么这个数就叫做a
的平方根(或二次方根).
这就是说,如果x
2
=
a
,那么
x
就叫做
a
的平方根.a的平方根记为±
2.
平方根的定义:
3.平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
4.立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作
.
5.立方根的性质:
平方根、立方根概念及性质
你知道算术平方根、平方根、立方根联系和区别吗?
表示方法
性
质
开
方
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
算术平方根
平方根
立方根
1.求下列各数的算术平方根:
(1)
0.04;
(2)
1;
(3)
(-3)2
;
(4)
3.求下列各数的立方根:
(1)
121;(2)
16;
(3)
0
;
(4)
(-3)2
;
(5)
2.求下列各数的平方根:
(1)
-0.008;(2)
43;
(3)
-64;
(4)
(-3)3;
(5)
4.求下列各式的值:
求根也好,求值也好,关键要弄清它是什么意思,然后可以选择定义和性质来求.
不要搞错了
64
±8
8
-4
___.
-4,-3,-2,-1,
0,1,2,3
一、平方根和立方根
1.
16的平方根是_____,符号表示为_____;
16的算术平方根是____,符号表示为_____.
2.
27的立方根是____,符号表示为_____.
3.下列数中的无理数是______________
-1,
,0.3,
,
0
,
0.101
001
000
1…(相邻两个1之间0的个数逐次加1).
3
4
0.101
001
000
1…
=
2
=2
利用定义
无理数也有乘除运算,在后面的章节里将会学习,也满足先定符号,再计算.
三、实数的运算
不要遗漏哦!
解下列方程:
当方程中出现平方时,若有解,一般都有两个解
当方程中出现立方时,一般都有一个解
1.
解:
2.
解:
掌握规律
注意平方根和立方根的移位法则
1、无限不循环的小数
叫做无理数.
有理数和无理数统称实数.
3、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
5、在进行实数的运算时,有理数的运算法则及运算性质同样适用。
2、实数与数轴上的点是一一对应的.
4、实数的大小比较方法有:利用数轴比较、利用绝对值比较、求平方比较、求差比较、求商比较和计算近似值比较等方法。
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1、判断下列说法是否正确:
1.实数不是有理数就是无理数。
(
)
2.无限小数都是无理数。
(
)
3.无理数都是无限小数。
(
)
4.带根号的数都是无理数。
(
)
5.两个无理数之积一定是无理数。(
)
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。(
)
有理数集合:{
};
1、把下列各数填在相应的大括号内:
整数集合:{
……};
奇数集合:{
……};
无理数集合:{
}。
-1
π,
2.1010010001…
2、把下列各数分别填入相应的集合内:
有理数集合
无理数集合
是负数
等于它的相反数
是正数
等于它本身
是负数
里面的数的符号
化简绝对值要看它
等于它的相反数
要学会计算哟!
计算:
3、已知
位置如图所示,
试化简
解:原式=-a-(b-a)+(c-a)-(c-b)
=-a-b+a+c-a-c+b=-a
解:原式=-(a+b-c)+(-b+2c)+(b-a)
=-a-b+c-b+2c+b-a
=-2a-b+3c
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
例题;求下列各数的相反数和绝对值
解:
相反数
绝对值
1、正实数的绝对值是
,0的绝对值是
,负实数的绝对值是
.
它本身
0
它的相反数
5、判断
(1)带根号的数都是无理数。
(2)无理数就是开方开不尽的数。
(3)有限小数是有理数,无限小数是无理数。
6、实数
在数轴上对应的点的位置关系如图所示,下列式子错误的是(
)
×
×
×
C
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
