2.3 二次函数图像与性质

(共26张PPT)
38岁的老乔丹第二次复出，在全场比赛还剩最后一秒钟时，华盛顿奇才队仍以2分落后于纽约尼克斯队，在这关键时刻，乔丹在三分线外出手！
已知篮球的飞行路线为抛物线，乔丹出手高度为2.37米，篮球在飞行了水平距离4米后达到最高点3.37米，问乔丹此次能否力挽狂澜？（三分线是以篮框中心在地面的投影为圆心，6.25米为半径的半圆；篮框的高度为3.05米）
动一动 说一说

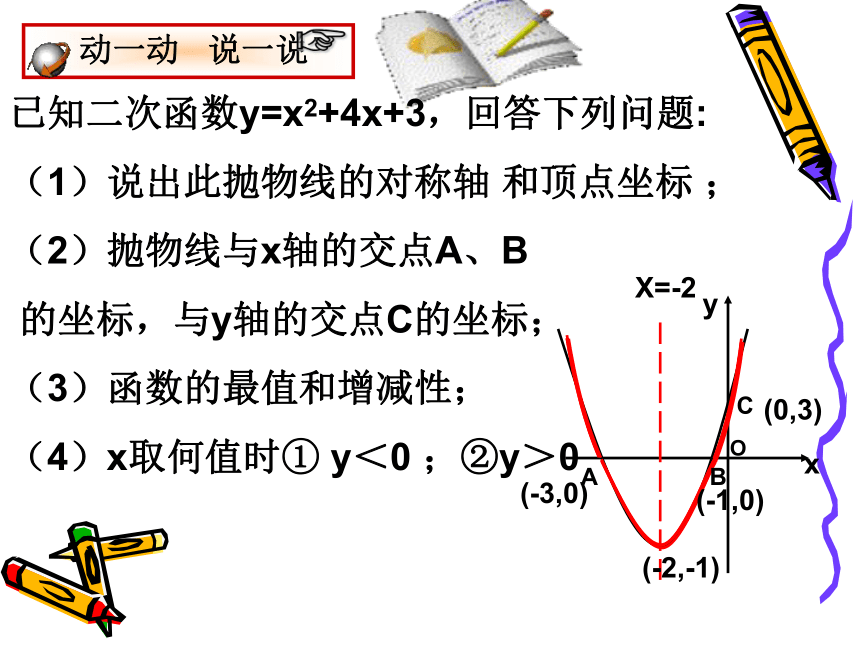
已知二次函数y=x2+4x+3，回答下列问题:
（1）说出此抛物线的对称轴 和顶点坐标 ；
（2）抛物线与x轴的交点A、B
的坐标，与y轴的交点C的坐标；
（3）函数的最值和增减性；
（4）x取何值时① y＜0 ；②y＞0
x
y
A
B
O
C
X=-2
(-3,0)
(-1,0)
(-2,-1)
(0,3)
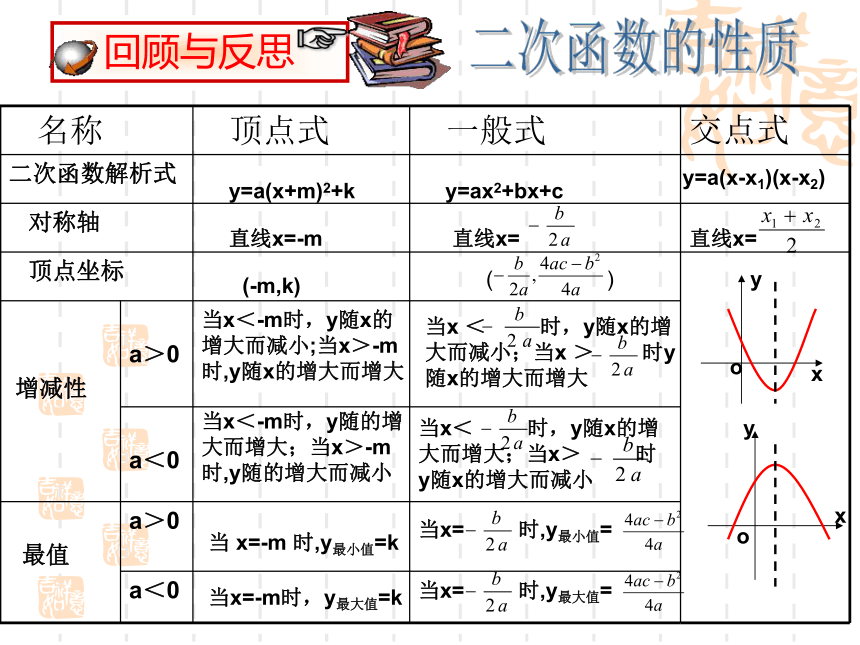
回顾与反思

名称 顶点式 一般式 交点式
二次函数解析式
对称轴
顶点坐标
增减性
a＞0
a＜0
最值 a＞0
a＜0
y=a(x+m)2+k
y=ax2+bx+c
y=a(x-x1)(x-x2)
直线x=-m
直线x=
直线x=
(-m,k)
( )
当x＜-m时，y随x的增大而减小;当x＞-m时,y随x的增大而增大
当x ＜ 时，y随x的增大而减小；当x ＞ 时y随x的增大而增大
当x＜-m时，y随的增大而增大；当x＞-m时,y随的增大而减小
当x＜ 时，y随x的增大而增大；当x＞ 时y随x的增大而减小
当 x=-m 时,y最小值=k
当x= 时,y最小值=
当x=-m时，y最大值=k
当x= 时,y最大值=
y
x
o
o
y
x
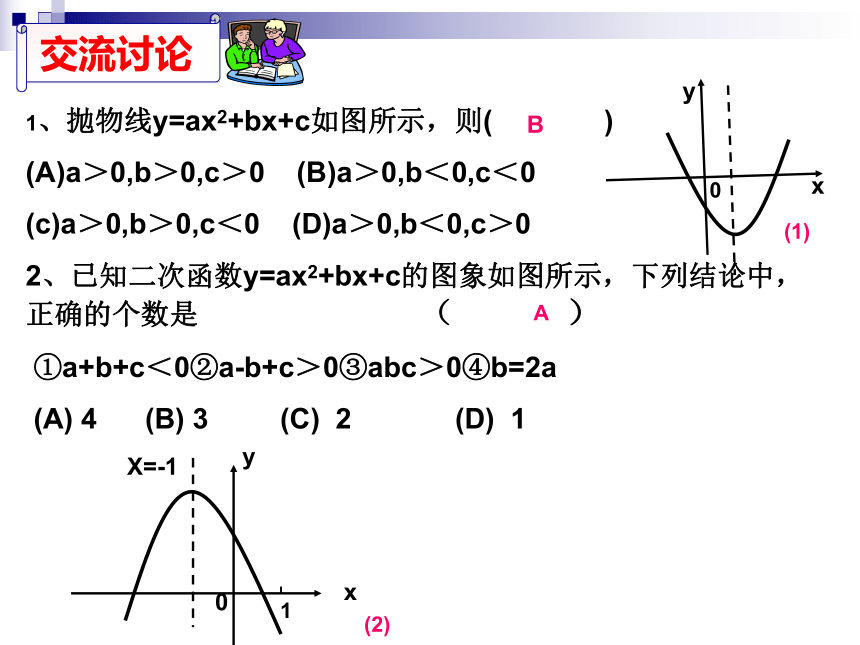
交流讨论
1、抛物线y=ax2+bx+c如图所示，则( )
(A)a＞0,b＞0,c＞0 (B)a＞0,b＜0,c＜0
(c)a＞0,b＞0,c＜0 (D)a＞0,b＜0,c＞0
2、已知二次函数y=ax2+bx+c的图象如图所示，下列结论中，正确的个数是 （ ）
①a+b+c＜0②a-b+c＞0③abc＞0④b=2a
(A) 4 (B) 3 (C) 2 (D) 1
x
y
0
x
y
X=-1
0
(2)
(1)
B
1
A
系数 性质
a
b
c
看开口方向 (上正、下负)
看与y轴交点 (上正、下负)
回顾与反思

看对称轴 (左同、右异)
开启 智慧
你说 我说
1、函数y=ax2+bx+c的图象如图所示。X= 为该函数图象的对称轴，根据这个函数图象，你能得到关于该函数的哪些性质和结论？
x
y
X=
o
-1
1
-1
(1)顶点在第四象限
（2）△＞0(与x轴有两个交点）
（3）当x＜　时，y随x的增大而减小
（4）当x＞　时，y随x的增大而增大
（5)a＞0
(6)b＜0
(7)abc＞0
(8)当x=-1时y＞0即a-b+c＞0
(9)当x=1时y＜0即a+b+c＜0
(10)-1＜c＜0
例：已知抛物线y=x2+(2n-1)x+n2-1(n为常数）
（1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数解析式；
（2）设A是（1）所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C。
①当BC=1时，求矩形ABCD的周长；
②试问矩形ABCD的周长是否存在最大值？如果存在，请你求出这个最大值，并指出此时A点的坐标；如果不存在，请说出你的理由。
尝试拓展 发展思维

行家看“门道”
如图是一个汽车隧道，形状成抛物线，隧道路面宽10米，顶部到地面的距离为10米.高4米，宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道？若此隧道是双向车道，那么这辆货车又能否顺利经过隧道？

10米
10米
10米
10米
10米
10米
2、已知抛物线y=(m-1)x2+4x-3开口向上，与x轴相交于A(x1,0)和B(x2,0)两点，其中x1＜x2
（1）求m的取值范围；
（2）若x12+x22=10，求抛物线的解析式，并在平面直角坐标系中画出这条抛物线；
（3）设这条抛物线的顶点坐标为C，延长CA交y轴于点D。在y轴上是否存在点P，使以P、O、B为顶点的三角形与△BCD相似？若存在，求出P点的坐标；若不存在，请说明理由。
课外 尝试
尝试热身练习
1、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同，则a= .
2、二次函数y=x2+1的图象的顶点坐标是 .
3、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .
4、二次函数y=x2-2x+2 当x= 时，y的最小值为 .
5、二次函数y=4x2+mx+1的图象顶点在x轴上，则m= ；若它的顶点在y轴上，则m= .
±2
(0,1)
直线x=-1
1
1
±4
0
X=
思考分析
我思,我进步
例2、有一抛物线沿x轴方向向右平移一个单位，再沿y轴方向向上平移一个单位，得到的抛物线为y=3x2-12x+16，求原抛物线的解析式。
知识源于悟
尝试热身练习
1、二次函数y=(x-2)2-1的图象的顶点坐标是 .
2、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .
3、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同，则a= .
4、二次函数y=4x2+mx+1的图象顶点在x轴上，则m= ；若它的顶点在y轴上，则m= ；
5、抛物线y=-2x2+4x-1向左平移3个单位，再向下平移2个单位，可得到抛物线的解析式为 .
6、二次函数y=ax2+bx+c的图象经过原点和第一、二、四象限，
则a 0, b 0 ,c 0 (填入＞、＜、或＝)
(1,2)
直线X=-1
±2
±4
0
y=-2(x+2)2-1
＞
＝
＜
y=ax2
y=a(x+m)2
y=a(x+m)2+k
y=ax2+k
向右或向左平移|m|个单位
（m＞0向左，m＜0向右）
向上或向下平移|k|个单位
（k＞0向上，k＜0向下）
向上或向下平移|k|个单位
（k＞0向上，k＜0向下）
向右或向左平移|m|个单位
（m＞0向左，m＜0向右）
想一想,做一做

1、已知关于x的二次函数y=x2+(k2-3k-4)x+2k的图象与x轴交于A、B两点，且这两点关于原点对称，求k的值。
2、已知二次函数y=2x2-(m+1)x+m-1.
（1）当m为何值时，函数图象过原点，并求出此时图象与x轴的另一个交点的坐标；
（2）如函数图象的顶点在第四象限，求m的取值范围。