7.5角的大小比较

(共20张PPT)
7.5角的大小比较预习指导：
1、边看165页至166页教材，边写出各个问题的答案，并归纳角的大小比较方法、角的分类及分类标准、角平分线的概念。
2、根据角平分线的概念，画出相应图形，并写出几何符号语言。
3、看例1时，要想一想（2）中怎样找直角、钝角、锐角才能防止遗漏，并思考为什么∠COE也是直角。
4、看例2时要特别注意书写格式。
5、若有疑问可向老师或其他同学请教。
回顾：
1、线段长短比较的方法：
2、线段的中点
如上图：点C把线段AB分成相等的线段AC和BC，点C叫做线段AB的中点
几何符号语言：
如图
∵点C为线段AB的中点
∴AC=BC=
AB
3、线段的和差倍分：
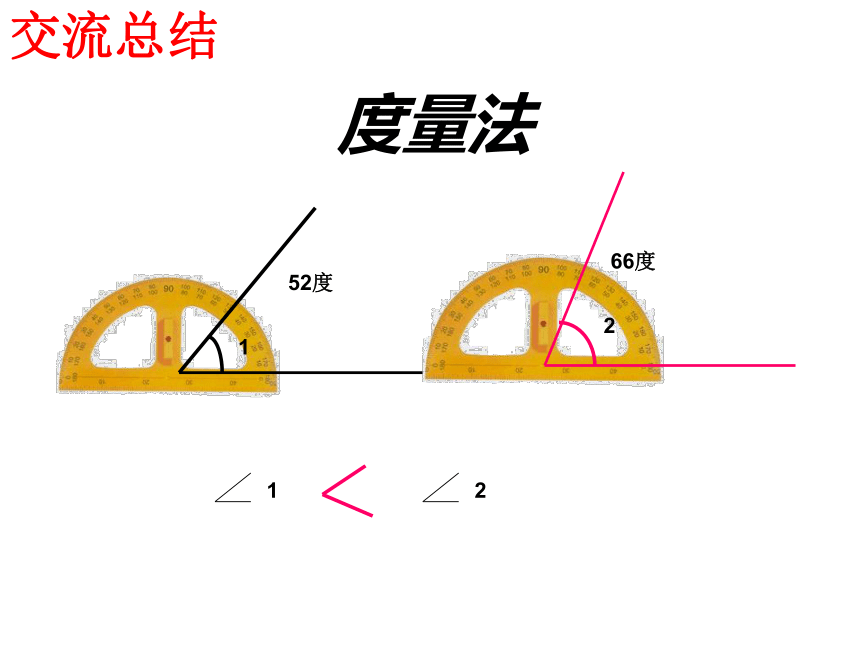
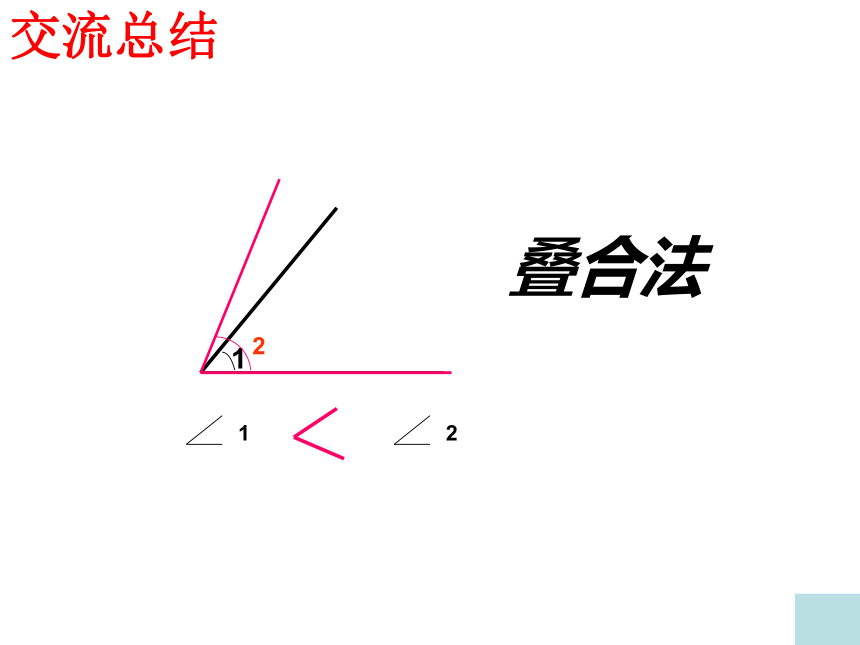
度量法、叠合法
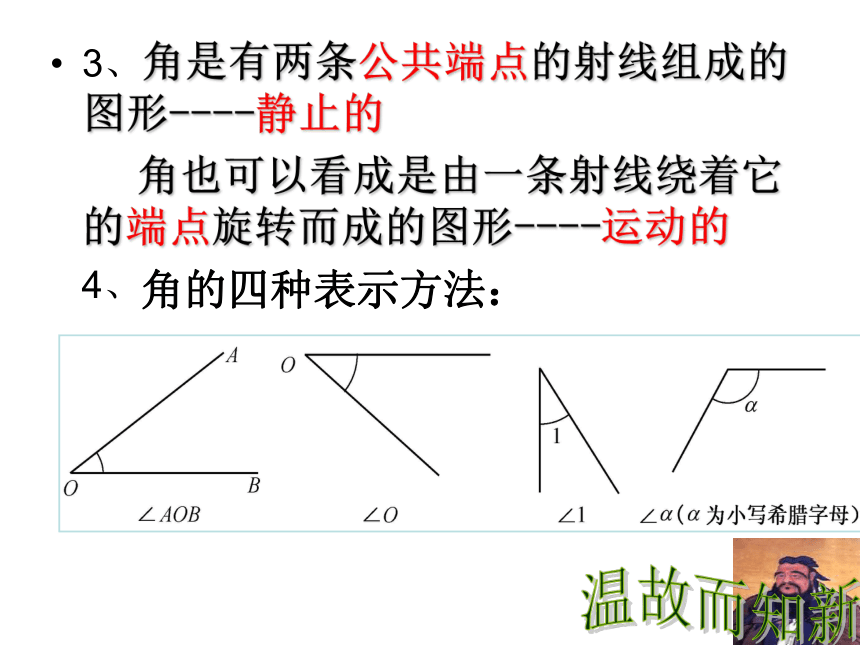
3、角是有两条公共端点的射线组成的图形----静止的
角也可以看成是由一条射线绕着它的端点旋转而成的图形----运动的
4、
角的四种表示方法：
碗窑初中
毛燕玲
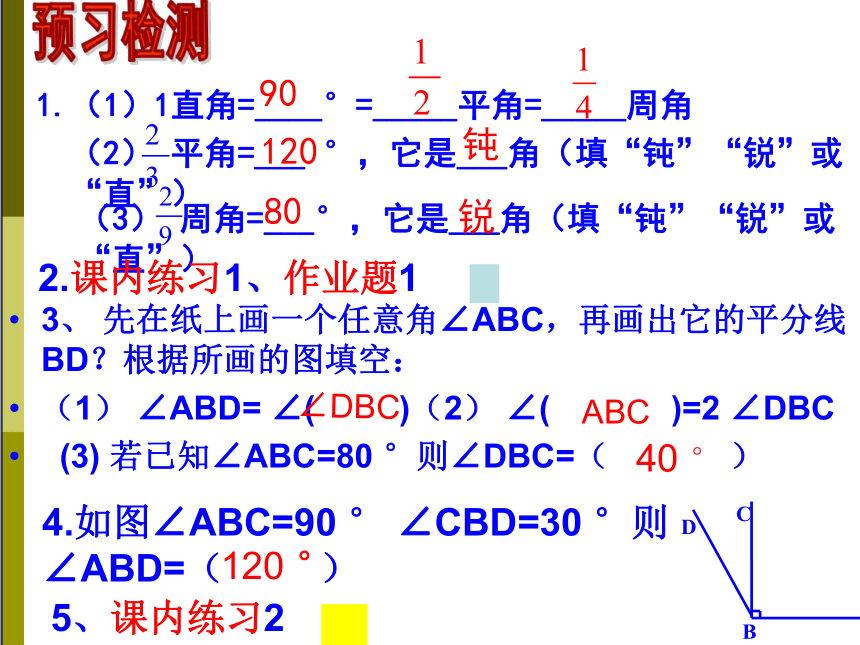
1.（1）1直角=____°=_____平角=_____周角
（2）
平角=___
°，它是___角（填“钝”“锐”或“直”）
（3）
周角=___°，它是___角（填“钝”“锐”或“直”）
90
120
钝
80
锐
2.课内练习1、作业题1
C
A
B
D
4.如图∠ABC=90
°
∠CBD=30
°则∠ABD=（
）
5、课内练习2
120
°
3、
先在纸上画一个任意角∠ABC，再画出它的平分线BD？根据所画的图填空：
（1）
∠ABD=
∠(
)（2）
∠(
)=2
∠DBC
(3)
若已知∠ABC=80
°则∠DBC=（
）
∠DBC
ABC
40
°
预习检测：
课内练习1.先观察下列各组角，并估计其中哪一个角较大，然后用量角器量一量，看看你的估计是否正确。
1
2
а
в
（1）
（2）
作业题1.∠α
=
12.30°与∠β
=
12°30′这两个角一样大吗？为什么？
∠1＞
∠2
∠
α<
∠β
方法1：∵
∠α
=
12.30°=12
°18
′
∠β
=
12°30′
∴
∠
α<
∠β
方法2：∵
∠α
=
12.30
°
∠β
=
12°30′=12.5°
∴
∠
α<
∠β
预习检测：
课内练习2.根据图形填空：
（1）
∠
AOB=
∠
AOC+
（
　　
）；
（2）
∠
AOD=
∠
AOB—（
　
　）=（
　
）—∠COD；
（3）
∠
AOC+
∠BOD—∠
AOB=（　　　）
Ｂ
Ａ
Ｄ
Ｃ
Ｏ
∠ＢＯＣ
∠ＢＯＤ
∠ＡＯＣ
∠ＣＯＤ
52度
66度
1
2
1
2
度量法
交流总结
1
2
叠合法
1
2
交流总结
例题1：如图，点A、O、E在一条直线上，解答下列问题：
（1）比较∠AOB，∠AOC，∠AOD，∠AOE的大小；
A
O
B
C
D
E
解（1）由图可以看出：
∠AOB﹤∠AOC﹤∠AOD﹤∠AOE
（2）图中的直角有∠AOC,∠BOD,∠COE
图中的锐角有∠AOB，∠BOC，
∠COD，∠DOE；
图中的钝角有∠AOD，∠BOE；
（2）找出图中的直角、锐角和钝角。
应用实践
A
O
B
C
D
E
变式二、如图∠
AOC=
∠
BOD=90
°
，
∠
AOD=125
°
，则
∠
BOC=（
）．
变式三、.如图∠
AOC=
∠
BOD=90
°
则∠AOD+
∠BOC=(
)
C
A
O
B
D
A
D
B
C
O
55
°
180
°
变式一:如图A、O、E在一直线上，
∠
AOC=
∠
BOD=90
°
∠
BOC=30
°则∠
AOD=（
）
∠DOE=（
）
150
°
30
°
应用实践
例2
解：
∴
∠
ABD=
∠
ABC+
∠
CBD=
90°+
30°
=120
°
∴
∠
ABP=
?
∠
ABD=
?
×
120
°=60
°
　　　　
D
C
P
A
B
如右图，
∠
ABC=90°
，
∠
CDB=30°
，
BP平分
∠
ABD。求∠
ABP的度数。
∵
∠
ABC=90°
，
∠
CDB=30°
∵
BP平分∠
ABD，
应用实践
变式一（书本课内练习3）:　如图，点Ｏ在直线ＡＣ上，∠
AOB＝５５
°
。画出∠
BOＣ的角平分线ＯＤ，并计算∠
AOＤ的度数。
Ｂ
Ａ
Ｃ
Ｏ
应用实践
变式二：
已知O为直线AB上一点，OE平分∠AOC，OF平分
∠COB,求∠EOF的大小？
解：
∵
OE平分
∠
AOC，OF平分
∠COB
∴∠EOF=∠2+∠3
=1／2(∠1+∠2+∠3+∠4)
=1／2∠AOB
=90°
∴∠1=∠2=
∵∠AOB=∠1+∠2+∠3+∠4=180°
（平角的意义）
A
B
E
C
F
O
1
2
3
4
∠BOC
∠AOC,
∠3=∠4=
（角平分线的意义）
（书本作业题5）
应用实践
.变式三：
如图，OC是∠AOB的任意一条射线，
OD平分∠AOC，OE平分∠BOC。
问∠DOE与∠AOB有什么关系？
E
C
D
A
B
O
应用实践
已知∠AOB=145°和∠AOC=25°
则∠BOC=---------------------
分类
思想
170
°或120
°
B
A
O
B
C
C
O
A
你的收获!你的困惑!
请你说一说:
你的新想法和新发现.
1、课本作业题6、7
2、作业本
1、如图，OC平分∠AOB，下列说法错误的是(
)
A.∠1=∠2
B.
∠AOB=2∠1
C.∠1+∠2=∠AOB
D.
∠1=∠AOB
A
O
B
C
1
2
2、下列说法中正确的是(
)
A
两个角的和为180°，那么这两个角都是直角
B
一个钝角一定大于一个锐角
C
大于90°的角叫做钝角
D
钝角与锐角的差为90°
课堂检测
3、根据图形填空
（1）∠AOC=∠AOB
-____
=
____
-∠COD
C
A
D
B
O
(2)若∠AOC=30°，∠BOC=80°，射线OC平分∠AOD，
则∠COD=______,∠BOD=______,