7.5一次函数的简单应用（1）

(共12张PPT)
一次函数的简单应用(1)
如图，已知直线L经过A,B两点,请根据图象回答:
(0,6)
(4,8)
y=0.5x+6
一次函数解析式求解的
常用方法是:待定系数法
(1):点A的坐标是_____;点B的坐标是_____;
(2):直线AB的解析式是___________;
做一做
x
O
2
4
6
2
(kg)
8
4
6
A
B
L
(cm)
x
O
2
4
6
2
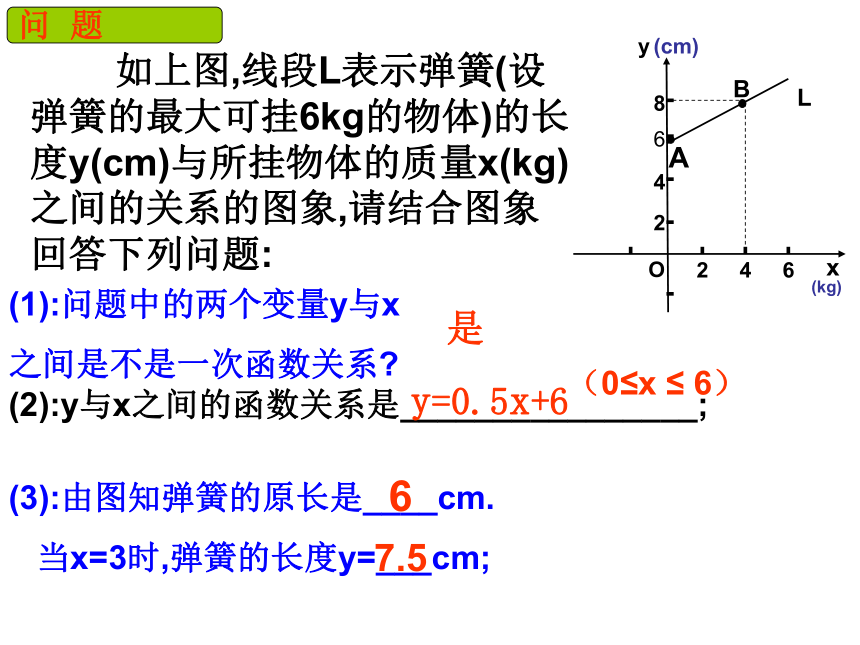
(1):问题中的两个变量y与x
之间是不是一次函数关系
(2):y与x之间的函数关系是________________;
(3):由图知弹簧的原长是____cm.
当x=3时,弹簧的长度y=___cm;
(kg)
是
y=0.5x+6
7.5
6
（0≤x ≤ 6）
问 题
如上图,线段L表示弹簧(设弹簧的最大可挂6kg的物体)的长度y(cm)与所挂物体的质量x(kg)之间的关系的图象,请结合图象回答下列问题:
y
8
4
6
A
B
L
(cm)
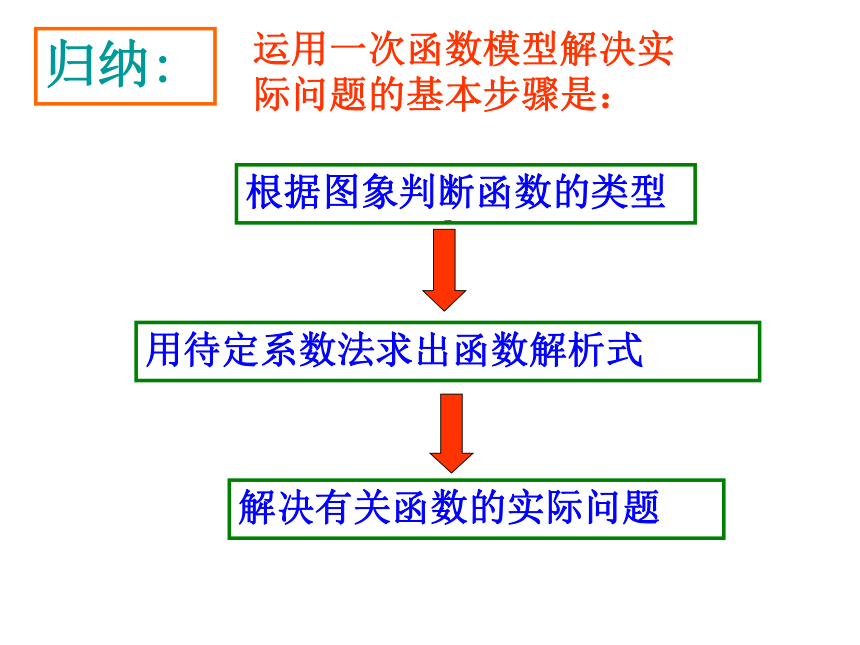
归纳:
运用一次函数模型解决实际问题的基本步骤是：
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
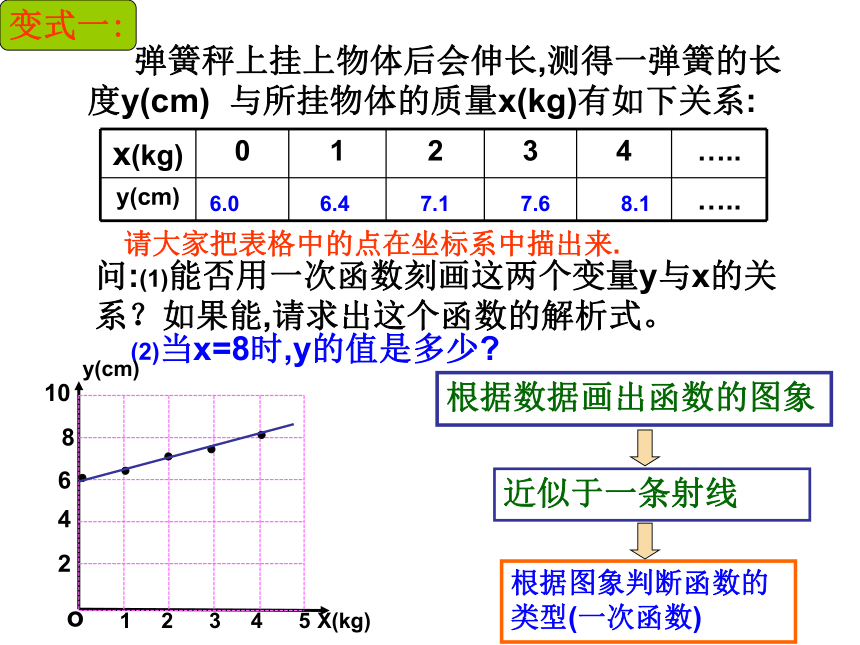
弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
x(kg) 0 1 2 3 4 …..
y(cm) …..
问:(1)能否用一次函数刻画这两个变量y与x的关系？如果能,请求出这个函数的解析式。
变式一:
(2)当x=8时,y的值是多少
6.0
7.1
7.6
6.4
8.1
o
1 2 3 4 5
2
4
6
8
10
y(cm)
X(kg)
根据数据画出函数的图象
请大家把表格中的点在坐标系中描出来.
近似于一条射线
根据图象判断函数的类型(一次函数)
变式二:
弹簧秤上挂上物体后会伸长,测得一弹簧的长度y(cm) 与所挂物体的质量x(kg)有如下关系:
问:(1)能否用一次函数刻画这两个变量y与x的关系？
如果能,请求出这个函数的解析式。
x(kg) 0 1 2 3 4 …..
y(cm) …..
6.0
7.0
7.5
6.5
8.0
(2)当x=8时,y的值是多少
寻找数据间的规律
得出函数的解析式
解决有关函数的实际问题
归纳:
能
y=0.5x+6
y=10
通过实验获得数据
根据数据画出函数的图象
根据图象判断函数的类型
用待定系数法求出函数解析式
解决有关函数的实际问题
寻找数据间的规律
得出函数的解析式
运用一次函数的模型解决实际问题过程
x
o
1 2 3 4 5
2
4
6
8
10
12
14
16
18
20
Y（m）
X（米）
蓝鲸
生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表（单位：米）：
吻尖到喷水孔的长度x（m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
问：能否用一次函数刻画这两个变量x与y的关系？如果能，请求出这个函数的解析式。
富阳市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
(1):分别写出0≤x≤15和x>15时,y与x的函数关系式;
O
15
20
39.5
27
x
吨
元
y
A
B
典型例题分析
解题思路：
关键是识别自变量在不同的取值范围内所对应函数的类型
用待定系数法分别求出不同范围内的函数解析式
分段函数
(2):若某用户该月用水21吨,
则应交水费多少元
10 20 30 40 50 60
O
t(分)
S(km)
1
2
周末小明从家里骑车去大润发超市购物，然后从超市返回家中。小明离家的路程s(km)和所经过的时间t（分）之间的函数关系如图所示，请根据图象回答下列问题：
(1):小明去超市途中的速度是多少？回家途中的速度是多少？
小明在超市逗留了多少时间？
(2):用恰当的方式表示小明回家的路程s(km)和所经过的时间t(分)之间的函数关系。
0.2km/分
0.1km/分
30分钟
A
C
∴s=- 0.1t+6
(40≤t≤60)
尝试园地2
(3):如图,折线OABC是S与t之间的函数关系的图象,请用函数关系式表示;
B
S=
0.2t
(0≤t≤10)
(40≤t≤60)
- 0.1t+6
2
(10为了绿化校园,富春街道给我校送来了一棵山毛榉和一棵枫树，山毛榉高2.4m，枫树高0.9m。山毛榉的平均生长速度是每年长高0.15m，枫树的平均生长速度是每年长高0.3m.请根据上述回答下列问题:
枫树
山毛榉
思考:
本题能否借助于一次函数的图象来解决
拓展与提高
(1):分别求出枫树的生长高度y1(米) 、山毛榉的生长高度y2(米)与时间x(年)的函数关系式.
(2):多少年后,两种树的树高相同
(3):多少年后枫树将比山毛榉高？
图象法
实际问题
数据获得
描点画图
猜想类型
求解验证