7.3一次函数(2)

(共26张PPT)
3、一次函数的解析式是什么？
y=kx
（k为常数，且k≠0）
y=kx+b
（k、b为常数，且k≠0）
当b=0时，
一次函数y=kx+b就变形为正比例函数y=kx
2、正比例函数的解析式是什么？
温故知新
1、一次函数和正比例函数的定义
1、“话吧”推出一项服务——长途电话，1分钟3毛，写出长途电话费y（元）和长途电话通话时间x（分）的关系
2、“联通公司”的一种移动通讯服务的收费标准为：每月基本服务费30元，每月免费通话时间为120分钟，以后每分钟收费0.4元，写出每月通话费y关于通话时间x（x≥120）的函数解析式.
3、“移动公司”的一种移动通讯服务的收费标准为：每月基本服务费30元，不提供免费通话时间，每分钟收费0.2元，写出每月通话费y关于通话时间x的函数解析式.
y=0.3x
y=30+0.4（x-120）=0.4x-16
即 y=0.4x-16
y=30+0.2x
做一做
4、下面四个函数哪个不是一次函数（ ）
A. y=0.3x
B. y=0.4x-16
C.
D.
5、下面三个函数哪个不是正比例函数（ ）
A. y=0.3x
B. y=0.4x-16
C.
6、分别写出下列一次函数的一次项系数k和常数项b的值
1） s = - t +4
2） y=-2（x-1）+x
D
B
做一做
(2) 若x=1，y=5，则函数关系式 _______.
7、已知正比例函数y=kx(k≠0)
y=5x
8、若y与x成正比例，且当x=0.5时，y=3，则y与x的关系式为_______
y=6x
y= x
1
3
做一做
(1) 若比例系数为 , 则函数关系式为_____；
9.已知一次函数y=kx+1,在x=2时，y=-3，则k= .
10.若一次函数y=kx+b，当x=-1时，y=2；当x=3时，y=-2；则k=____,b=____
-1
1
如何确定正比例函数和一次函数解析式
-2
做一做
确定正比例函数的表达式需要一个条件
确定一次函数的表达式需要两个条件
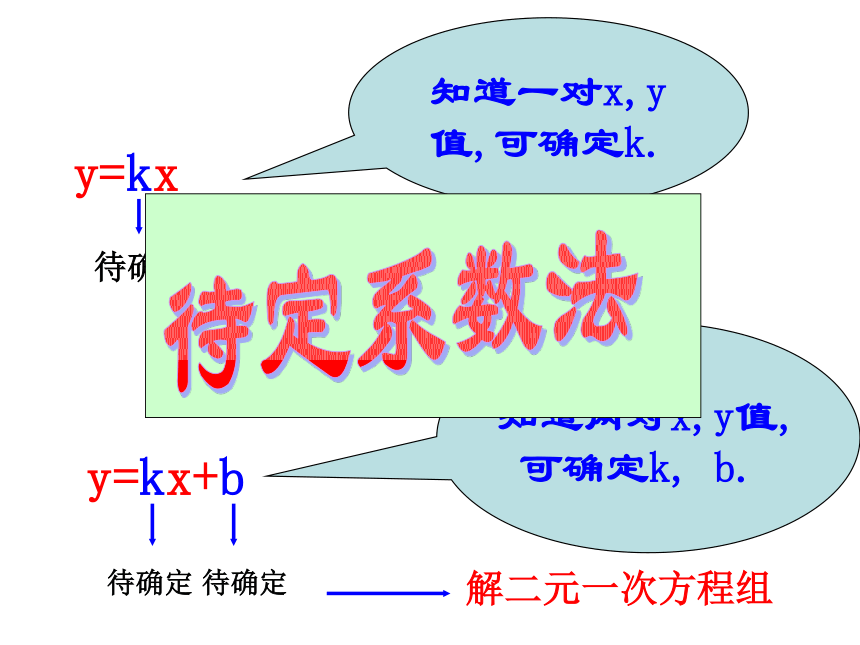
y=kx
y=kx+b
知道一对x,y值,可确定k.
知道两对x,y值,可确定k, b.
待确定
待确定
待确定
解一元一次方程
解二元一次方程组
例1、已知y是x一次函数，当x=3时， y=1；当x=-2时， y=-14 。
（3）当y=4时自变量x的值？
（2）当x=5时函数y的值；
（1）求这个一次函数的关系式和自变量x的取值范围；
解：（1）设y=kx+b，由已知得
3k+b=1
-2k+b=-14
解得：k=3，b=-8
∴这个一次函数的解析式为：y=3x-8 （x为任何实数）
（2）当x=5时，y=15-8=7
（3）当y=4时，3x-8=4 解得x=4
1、设：所求的一次函数解析式为y=kx+b；
2、列：依已知列出关于k、b的方程组；
3、解：解方程组，求得k、b；
4、写：把k、b的值代入y=kx+b ，写出一次函数解析式。
用待定系数法求一次函数解析式的一般步骤是怎样的呢
例2、已知y+m与x-1成正比例，当x=-1时，y=-15 ；当x=7时，y=1。求:
（2）当-3＜y＜7时，自变量x的取值范围；
（1）y关于x的函数解析式；
解：（1）设y+m=k（x-1），即y=kx-k-m，由已知得：
-k-k-m=-15
7k-k-m=1
解得：k=2，m=11
∴y关于x的函数解析式是 y=2x-13
（2）当-3＜y＜7时，即-3＜2x-13＜7，解得5＜x＜10
4、已知y-100与x成正比例，且当x=10时,y=600.
（1）求y关于x的函数解析式.
（2）当-300＜y≤400时, 自变量x的取值范围。
解:
把x=10时，y=600代入y-100=kx，得
（1）设这个正比例函数解析式为 y-100=kx
解得
k=50
∴y-100=50x
600-100=10k
即y=50x+100
（2）当-300＜y≤400时， -300＜50x+100 ≤400
∴自变量x的取值范围为-8＜x≤6
例3、按某饮料厂生产一种饮料，经测算，用1吨水生产的饮料所获利润y（元）是1吨水的买入价x（元）的一次函数。根据下表提供的数据，求y关于x的函数解析式；并求当水价为每吨10元时，1吨水生产的饮料所获的利润是多少？
1吨水的买入价（元） 4 6
利润y（元） 200 198
例4、某地区从1995年底开始，沙漠面积几乎每年以相同的速度增长。据有关报道，到2001年底，该地区的沙漠面积己从1998年底的100.6万公倾扩展到101.2万公倾。
（1）可选用什么数学方法来描述该地区的沙漠面积的变化？
（2）如果该地区的沙漠化得不到治理，那么到2020年底，该地区的沙漠面积将增加到多少万公倾？
例4、某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到多少公顷
解:
（1）设95年年底沙漠面积为b万公顷，每经过一年，沙漠面积增加k万公顷，经过x年，沙漠面积为y万公顷，由题意得 y=kx+b
且当x=3时，y=100.6；当x=6时，y=101.2
把x=3时，y=100.6；x=6时，y=101.2分别代入y=kx+b，得
100.6=3k+b
101.2=6k+b
①
②
解得
k=0.2
b=100
∴y=0.2x+100
（2）当x=25时，y=0.2×25+100=105
答：（略）
解: 设y=kx+b,根椐题意，得
14.5=b ①
16=3k+b ②
把b=14.5代入②，得 k=0.5
所以在弹性限度内：y=0.5x+14.5
当x=4时，y=0.5 × 4 + 14.5 = 16.5
答：物体的质量为4千克时，弹簧长度为16.5厘米。
｛
练一练
1、在弹性限度内，弹簧的长度y（厘米）是所挂物 体质量x（千克）的一次函数。一根弹簧不挂物体时长14.5厘米；
当所挂物体的质量为3千克时，弹簧长16厘米。写出y与x之间
的关系式，并求当所挂物体的质量为4千克时弹簧的长度。
2、很多城市的出租车按里程收费：在一定的里程内按定额收费（起步价），超出规定里程部分按与超出里程成正比例收费。某市出租车的起步价里程为4km，起步价为10元（不计等待时间）
（1）小明一次在该市乘车，从计费表上看到乘车里程和车费分别为6km，14.00元，请用函数解析式表示出租车超出起步价里程时的计费方法；
（2）如果你在该市乘坐出租车的里程为3km，那么需付多少车费？如果乘车里程为8km呢？
练一练
3、按一航空公司规定旅客可免费托运一定质量的行李，超过规定质量的行李需买行李票，行李票费用y（元）是行李质量x（kg）的一次函数。己知当行李的质量分别为20kg，40kg时，需支付的行李票费用为15元和45元，求y与x之间的函数解析式。
练一练
4、按某长途汽车客运公司规定旅客可随身携带一定质量的行李，如果超过规定的质量，则需要购买行李票。已知行李费y元是关于x千克的一次函数，王先生带60千克行李需付6元行李费，张先生带80千克行李需付10元行李费。
（1）求y与x之间的函数解析式。
（2）问旅客最多可免费携带行李多少千克？
练一练
5、按某商店购进一批单价为16元的日用品，销售一段时间后，为了获取更多利润，商店决定提高销售价格。经试验发现，若按每件20元的价格销售时，每月能卖出360件；若按每件25元的价格销售时，每月能卖出210件。假定每月销售件数y件是单价x元的一次函数.
（1）求y关于x的函数解析式；
（2）若按每件30元的价格销售，则每月可卖出几件？这个月的利润是多少？
练一练
6、按拖拉机的油箱最多可装油56kg，犁地时平均每小时耗油6kg，现装满油后去犁地。
（1）写出油箱中剩余油Q（kg）与犁地时间t（时）之间的函数关系。
（2）求函数自变量的取值范围。
（3）求拖拉机工作4时30分后，油箱中剩多少千克油？
练一练
这节课我们主要学习了哪些内容
用待定系数法求一次函数的解析式.
1、爸爸准备为小明买一双新的运动鞋，但要小明自己算出穿几码的鞋．小明回家量了妈妈３６码的鞋长２３厘米，爸爸４１码的鞋子长２５.５厘米．你能帮小明算算他穿的２１.５厘米长的鞋是几码吗？看看你自己穿的鞋子的码数和长度是否也符合你所发现的规律？
课外拓展：
2、按近几年，我国经济快速发展，电力需求最大，供应不足，某市为了鼓励居民节约用电，对居民用电收费采取了价格浮动政策；每户居民每月用电不超过20度时，每度电费0.5元；超过20度时，超过部分每度电费0.6元。该市民王先生家七月份用电x度。
1）求王先生家应付电费y元与用电量x之间的函数解析式
2）若王先生家该月用电80度，求他需付的电费；
3）若王先生家该月付电费22元，求他家该月的用电量；
课外拓展：
1、已知一次函数y=kx+2，当x=5，y=4时，求这个一次函数的解析式.
3、已知y是x的一次函数，当x=3时， y=1；x=-2时， y=-14 ，（1）求这个一次函数的关系式和自变量x的取值范围；（2）当x=5时，求函数y的值；（3）当y=4时，求自变量x的值.
2、已知y是x一次函数，当x=-2时，y=7；当x=3时， y=-5。求y关于x的函数解析式；
练一练