浙教版数学九上1.1二次函数课件(19张ppt)
文档属性
| 名称 | 浙教版数学九上1.1二次函数课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 809.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-11 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第一章
二次函数
1.1
二次函数
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
1、一元二次方程的一般形式是?
ax2+bx+c=0
(a、b、c是常数,a≠0)
2.我们已学过哪些函数?
一次函数
y=kx+b(k、b是常数,k≠0)
反比例函数
请用适当的函数解析式表示下列问题情境中的两个变量
y
与
x
之间的关系:
1、圆的半径是x(cm),则它的面积y与半径x之间的函数关系式是
.
y=
x2
2、王先生存入银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期.两年后王先生共得本息y元与年存款利率x之间的函数关系式是
y=2(1+x)2=2x2+4x+2
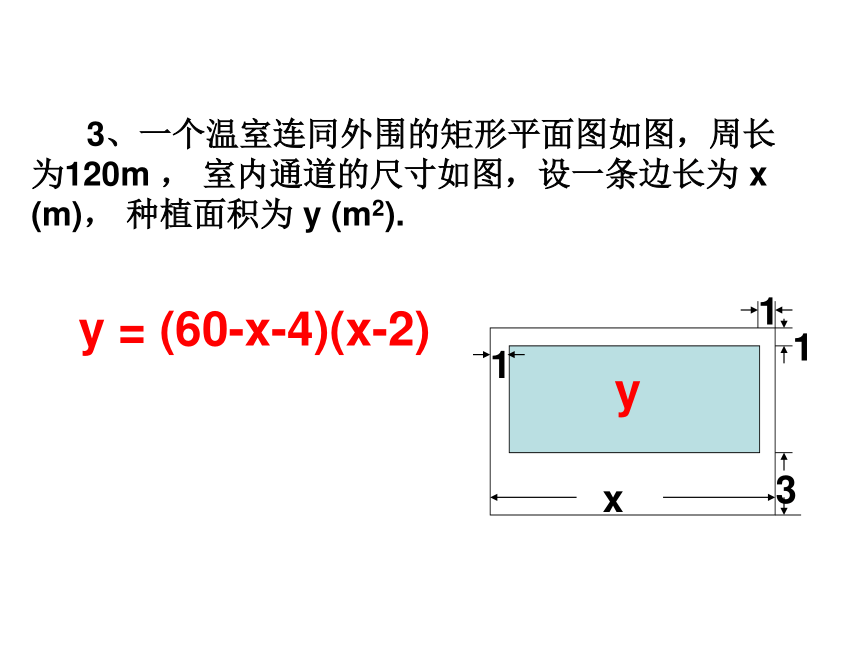
3、一个温室连同外围的矩形平面图如图,周长为120m
,
室内通道的尺寸如图,设一条边长为
x
(m),
种植面积为
y
(m2).
1
1
1
3
x
y
=
(60-x-4)(x-2)
y
上面三个表达式中,函数表达式具有什么共同特征?
y=x2
y=2(1+x)2=2x2+4x+2
y
=
(60-x-4)(x-2)=-x2+58x-112
自变量的最高次数都是2
二次函数的定义:
一般地,若两个自变量x,y之间的对应关系可以表示成y=ax?+bx+c(a,b,c是常数,a≠
0)的形式,则称y是x的二次函数.
归纳总结
a为二次项系数,ax2叫做二次项;
b为一次项系数,bx叫做一次项;
c为常数项.
提示:(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠
0;
(3)等式的右边最高次数为
2,可以没有一次项和常数项,但不能没有二次项;
(4)x的取值范围通常是任意实数
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
1、下列函数中,哪些是二次函数?
是
不是
是
是
不是
先化简后判断
2、分别说出下列二次函数的二次项系数、一次项系数和常数项。
解:(1)二次项系数:1,一次项系数0,常数项1;
(2)二次项系数:-3,一次项系数7,常数项-12;
(3)二次项系数:-2,一次项系数2,常数项0.
(l)求y关于
x的函数解析式和自变量x的取值范围。
(0(2)当x分别为0.25,0.5,1,1.5,1.75
时
,求对应的四边形EFGH的面积y,并列表表示.
2
3.125
3.125
2.5
2.5
(3)随着x的取值的增大,y的值有怎样的变化?
随着x的取值的增大,y的值先变小后变大
x
0.25
0.5
1
1.5
1.75
y
解:把先x=1,y=4;x=2,y=-5分别代入函数式y=x2+bx+c,
1+b+c=4
4+2b+c=-5
得方程组
解得
b=-12
c=15
∴此二次函数的表达式为y=x2-12x+15
1、下列函数中,哪些是二次函数?
是
不是
是
不是
是
1
2
-1
1
0
0
0
-3
2
2、写出下列二次函数的二次项系数、一次项系数和常数项。
二次函数
二次项系数
一次项系数
常数项
4、矩形的周长为16cm,它的一边长为x
cm,面积为y
cm2.
(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x
(0<x<8)
(2)当x=3时,y=-32+8×3=15
(cm2
).
3、函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
A
.
m,n是常数,且m≠0
B
.
m,n是常数,且n≠0
C.
m,n是常数,且m≠n
D
.
m,n为任何实数
C
5、
(1)m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
解:
(1)由题可知
解得
(2)由题可知
解得
m=3.
第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
6、已知二次函数y=
ax2+bx+c,当x=2时,y=
3;当x=-2
时,y=
2;当x=
4
时,y=
2.求二次函数表达式。
解:把x=2,y=
3;x=-2
,y=
2;当x=
4
,y=
2分别函数式,
得到方程组
4a+2b+c=3
4a-2b+c=2
16a+4b+c=2
解得
二次函数
定
义
y=ax2+bx+c(a
≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a
≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a
≠0,a,b,c是常数).
第一章
二次函数
1.1
二次函数
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
1、一元二次方程的一般形式是?
ax2+bx+c=0
(a、b、c是常数,a≠0)
2.我们已学过哪些函数?
一次函数
y=kx+b(k、b是常数,k≠0)
反比例函数
请用适当的函数解析式表示下列问题情境中的两个变量
y
与
x
之间的关系:
1、圆的半径是x(cm),则它的面积y与半径x之间的函数关系式是
.
y=
x2
2、王先生存入银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期.两年后王先生共得本息y元与年存款利率x之间的函数关系式是
y=2(1+x)2=2x2+4x+2
3、一个温室连同外围的矩形平面图如图,周长为120m
,
室内通道的尺寸如图,设一条边长为
x
(m),
种植面积为
y
(m2).
1
1
1
3
x
y
=
(60-x-4)(x-2)
y
上面三个表达式中,函数表达式具有什么共同特征?
y=x2
y=2(1+x)2=2x2+4x+2
y
=
(60-x-4)(x-2)=-x2+58x-112
自变量的最高次数都是2
二次函数的定义:
一般地,若两个自变量x,y之间的对应关系可以表示成y=ax?+bx+c(a,b,c是常数,a≠
0)的形式,则称y是x的二次函数.
归纳总结
a为二次项系数,ax2叫做二次项;
b为一次项系数,bx叫做一次项;
c为常数项.
提示:(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠
0;
(3)等式的右边最高次数为
2,可以没有一次项和常数项,但不能没有二次项;
(4)x的取值范围通常是任意实数
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
1、下列函数中,哪些是二次函数?
是
不是
是
是
不是
先化简后判断
2、分别说出下列二次函数的二次项系数、一次项系数和常数项。
解:(1)二次项系数:1,一次项系数0,常数项1;
(2)二次项系数:-3,一次项系数7,常数项-12;
(3)二次项系数:-2,一次项系数2,常数项0.
(l)求y关于
x的函数解析式和自变量x的取值范围。
(0
时
,求对应的四边形EFGH的面积y,并列表表示.
2
3.125
3.125
2.5
2.5
(3)随着x的取值的增大,y的值有怎样的变化?
随着x的取值的增大,y的值先变小后变大
x
0.25
0.5
1
1.5
1.75
y
解:把先x=1,y=4;x=2,y=-5分别代入函数式y=x2+bx+c,
1+b+c=4
4+2b+c=-5
得方程组
解得
b=-12
c=15
∴此二次函数的表达式为y=x2-12x+15
1、下列函数中,哪些是二次函数?
是
不是
是
不是
是
1
2
-1
1
0
0
0
-3
2
2、写出下列二次函数的二次项系数、一次项系数和常数项。
二次函数
二次项系数
一次项系数
常数项
4、矩形的周长为16cm,它的一边长为x
cm,面积为y
cm2.
(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x
(0<x<8)
(2)当x=3时,y=-32+8×3=15
(cm2
).
3、函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
A
.
m,n是常数,且m≠0
B
.
m,n是常数,且n≠0
C.
m,n是常数,且m≠n
D
.
m,n为任何实数
C
5、
(1)m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
解:
(1)由题可知
解得
(2)由题可知
解得
m=3.
第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
6、已知二次函数y=
ax2+bx+c,当x=2时,y=
3;当x=-2
时,y=
2;当x=
4
时,y=
2.求二次函数表达式。
解:把x=2,y=
3;x=-2
,y=
2;当x=
4
,y=
2分别函数式,
得到方程组
4a+2b+c=3
4a-2b+c=2
16a+4b+c=2
解得
二次函数
定
义
y=ax2+bx+c(a
≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a
≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a
≠0,a,b,c是常数).
同课章节目录
