相似三角形的判定与性质2
图片预览






文档简介
(共34张PPT)
相似三角形的判定与性质
典例精讲
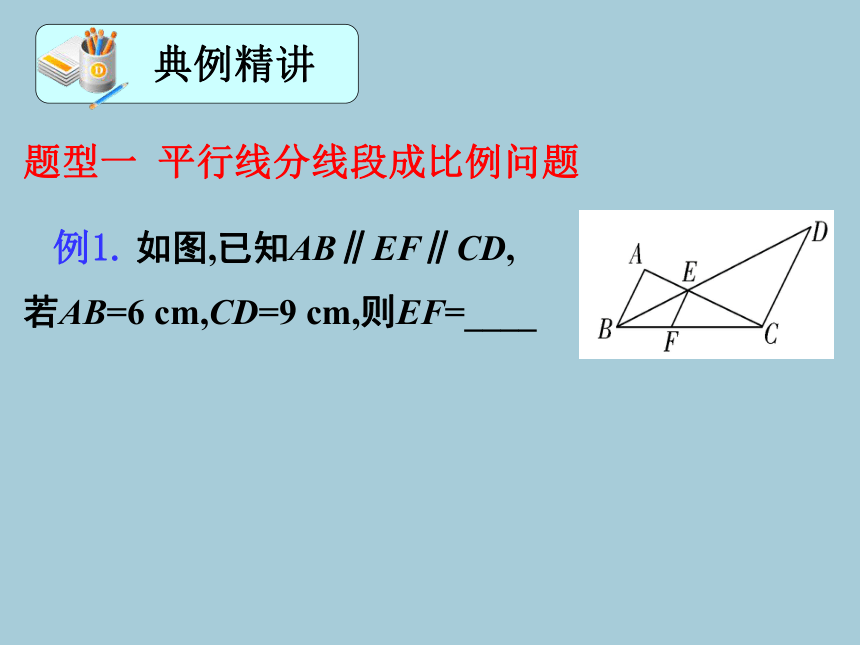
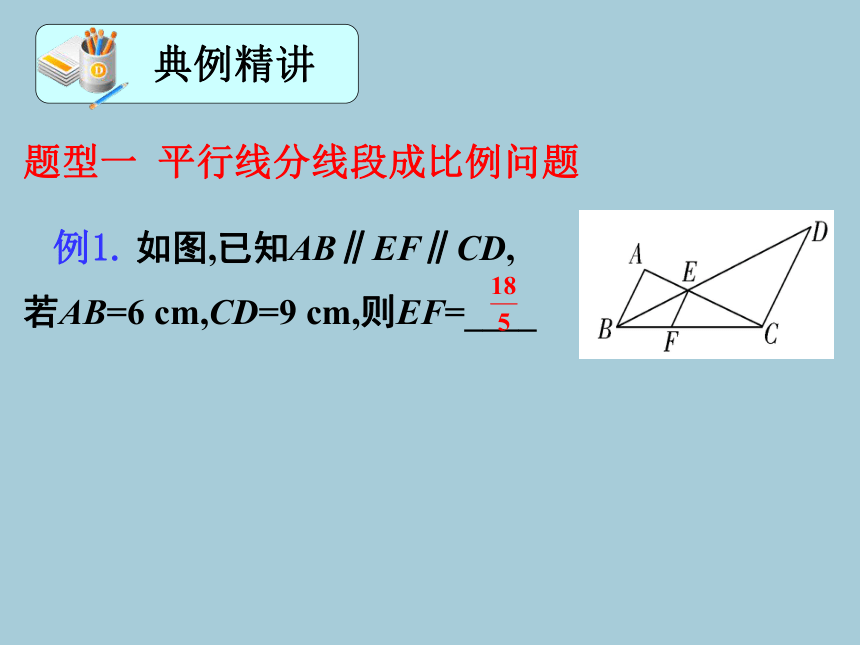
题型一 平行线分线段成比例问题
典例精讲
如图,已知AB∥EF∥CD,
若AB=6 cm,CD=9 cm,则EF=____
题型一 平行线分线段成比例问题
例1.
典例精讲
如图,已知AB∥EF∥CD,
若AB=6 cm,CD=9 cm,则EF=____
题型一 平行线分线段成比例问题
例1.
典例精讲
如图,已知AB∥EF∥CD,
若AB=6 cm,CD=9 cm,则EF=____
题型一 平行线分线段成比例问题
例1.
分析:由于BC是△ABC与△DBC的公共
边,且AB∥EF∥CD,利用平行线分三角形
成相似三角形可求EF.
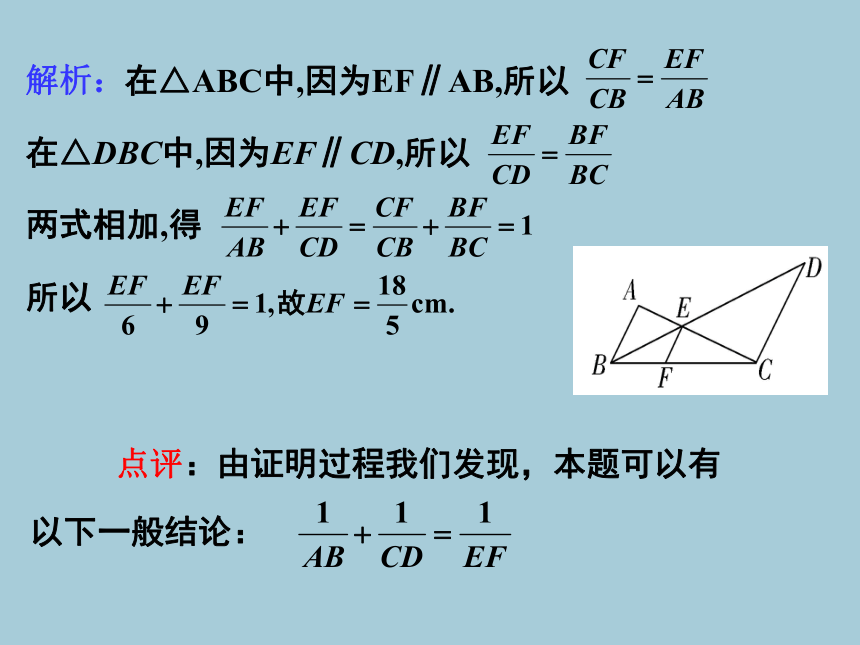
在△ABC中,因为EF∥AB,所以
在△DBC中,因为EF∥CD,所以
两式相加,得
所以
解析:
点评:由证明过程我们发现,本题可以有
以下一般结论:
在△ABC中,因为EF∥AB,所以
在△DBC中,因为EF∥CD,所以
两式相加,得
所以
解析:
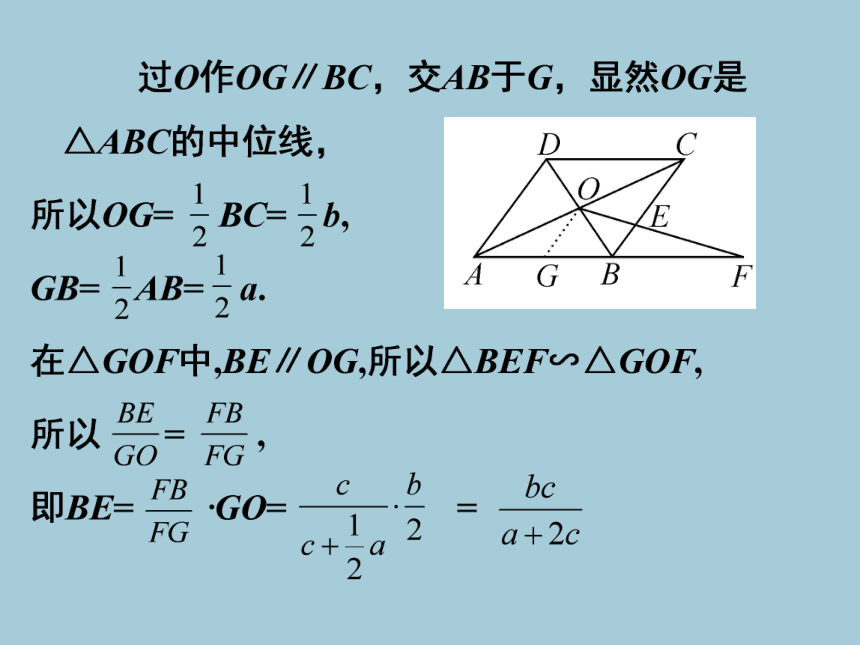
如右图,平行四边形ABCD的对角线交
于点O,OE交BC于E,交AB的延长线于F,
若AB=a,BC=b,BF=c,则BE=_________.
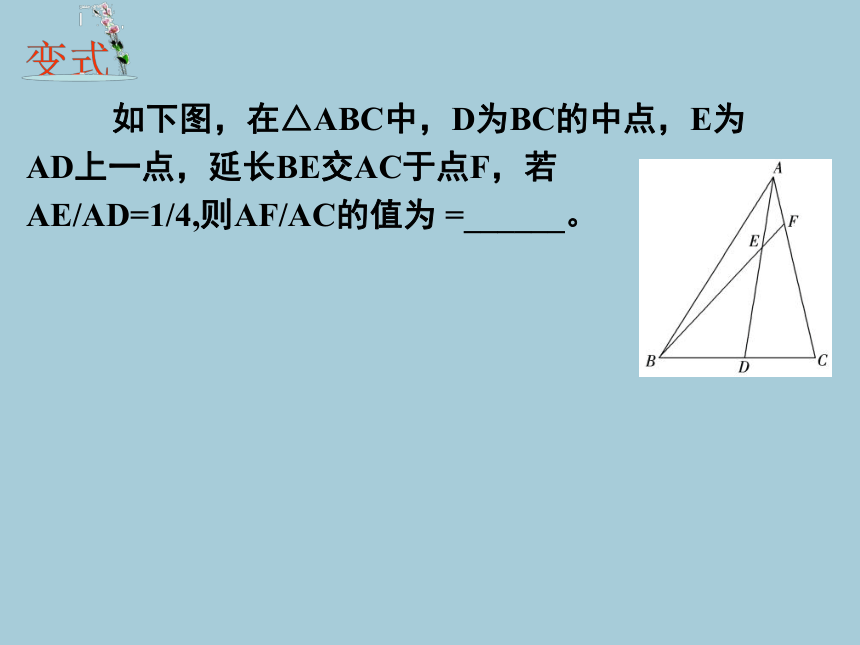
如下图,在△ABC中,D为BC的中点,E为
AD上一点,延长BE交AC于点F,若
AE/AD=1/4,则AF/AC的值为 =______。
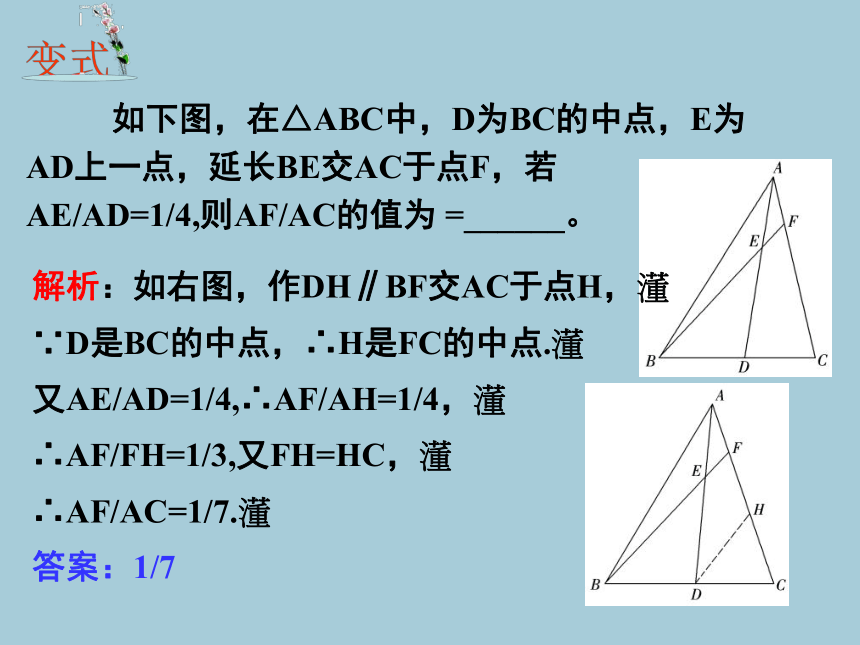
解析:如右图,作DH∥BF交AC于点H,
∵D是BC的中点,∴H是FC的中点.
又AE/AD=1/4,∴AF/AH=1/4,
∴AF/FH=1/3,又FH=HC,
∴AF/AC=1/7.
答案:1/7
如下图,在△ABC中,D为BC的中点,E为
AD上一点,延长BE交AC于点F,若
AE/AD=1/4,则AF/AC的值为 =______。
点评:在几何证明中,如果题目给的
条件较为分散,可以通过添加辅助线,使
分散的条件适当集中.如果能熟练掌握几个
基本图形,把所要证明的图形转化为基本
图形,可使证明思路更明确,更快捷.
题型二 直角三角形射影定理及应用
已知,如图,在梯形ABCD中,
AD∥BC,AC⊥BD,垂足为E,∠ABC=45°,过
E作AD的垂线交AD于F,
交BC于G,过E作AD的平
行线交AB于H.
求证:FG2=AF·DF+BG·CG+AH·BH.
题型二 直角三角形射影定理及应用
例2.
分析:由射影定理可知AF·DF=EF2,
BG·CG=EG2,故考虑将FG=FE+EG,然后只需
寻找EF·EG与AH·BH的关系.
分析:由射影定理可知AF·DF=EF2,
BG·CG=EG2,故考虑将FG=FE+EG,然后只需
寻找EF·EG与AH·BH的关系.
解析:因为AC⊥BD,故△AED、
△BEC都是直角三角形.
又EF⊥AD,EG⊥BC,由射
影定理可知AF·DF=EF2,
BG·CG=EG2.
点评:做平面几何证明题时要分析待证
明的结论与已知条件的关系,逐步消除差距.
如图,在Rt△ABC中,
∠BAC=90°,AD⊥BC
于D,DF⊥AC于F,DE⊥AB于E,求证:
AD3=BC·BE·CF.
如图,在Rt△ABC中,
∠BAC=90°,AD⊥BC
于D,DF⊥AC于F,DE⊥AB于E,求证:
AD3=BC·BE·CF.
分析:问题题设中含有直角三角形和斜边
上的高,符合直角三角形射影定理的两个条件
中,故考虑应用射影定理求解.
证明:
题型三 相似三角形判定定理及性质定理的应用
题型三 相似三角形判定定理及性质定理的应用
例3.
分析:要证明这四个三角形都相似,可以逐
次证明其中的三角形相似,由于这些三角形都是
直角三角形,因此只要证明两个三角形有一组锐
角相等或两组对应边
成比例即可.
分析:要证明这四个三角形都相似,可以逐
次证明其中的三角形相似,由于这些三角形都是
直角三角形,因此只要证明两个三角形有一组锐
角相等或两组对应边
成比例即可.
解析:
如右图所示,在△ABC中,AB=AC,AD是边BC的中线,P为
AD上一点,CF∥AB,BP的延长线分别交AC,CF于点E,F,
求证:BP2=PE·PF. ?
如右图所示,在△ABC中,AB=AC,AD是边BC的中线,P为
AD上一点,CF∥AB,BP的延长线分别交AC,CF于点E,F,
求证:BP2=PE·PF. ?
方法提炼
1.相似三角形的证法:①定义法:对应
边成比例,对应角相等;②平行法;③判定
定理法;④对直角三角形除以上方法外,还
有特殊方法,两直角边对应成比例,两直角
三角形相似;一条直角边和斜边对应成比
例,两直角三角形相似;斜边上的高分成的
两直角三角形与原三角形相似.
2.相似三角形的性质:①对应边成比例,
对应角相等;②对应高的比、对应中线的比、
对应角平分线的比、周长的比都等于相似比,
而面积的比等于相似比的平方;③相似三角形
外接圆的直径比、周长比等于相似比,外接圆
的面积比等于相似比的平方.利用这些关系可以
进行各种证明、求值.
3.在探究证明中,掌握从特殊到一般和化归
的思想方法,学会解决问题的程序、模式.
走进高考
(2009·江苏卷)如图,在四边
形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
走进高考
(2009·江苏卷)如图,在四边
形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
证明:由△ABC≌△BAD,得∠ACB=∠BDA,
故A、B、C、D四点共圆,从而∠CAB=∠CDB.
再由△ABC≌△BAD,得∠CAB=∠DBA.
因此∠DBA=∠CDB,所以AB∥CD.
练习讲评
相似三角形的判定与性质
典例精讲
题型一 平行线分线段成比例问题
典例精讲
如图,已知AB∥EF∥CD,
若AB=6 cm,CD=9 cm,则EF=____
题型一 平行线分线段成比例问题
例1.
典例精讲
如图,已知AB∥EF∥CD,
若AB=6 cm,CD=9 cm,则EF=____
题型一 平行线分线段成比例问题
例1.
典例精讲
如图,已知AB∥EF∥CD,
若AB=6 cm,CD=9 cm,则EF=____
题型一 平行线分线段成比例问题
例1.
分析:由于BC是△ABC与△DBC的公共
边,且AB∥EF∥CD,利用平行线分三角形
成相似三角形可求EF.
在△ABC中,因为EF∥AB,所以
在△DBC中,因为EF∥CD,所以
两式相加,得
所以
解析:
点评:由证明过程我们发现,本题可以有
以下一般结论:
在△ABC中,因为EF∥AB,所以
在△DBC中,因为EF∥CD,所以
两式相加,得
所以
解析:
如右图,平行四边形ABCD的对角线交
于点O,OE交BC于E,交AB的延长线于F,
若AB=a,BC=b,BF=c,则BE=_________.
如下图,在△ABC中,D为BC的中点,E为
AD上一点,延长BE交AC于点F,若
AE/AD=1/4,则AF/AC的值为 =______。
解析:如右图,作DH∥BF交AC于点H,
∵D是BC的中点,∴H是FC的中点.
又AE/AD=1/4,∴AF/AH=1/4,
∴AF/FH=1/3,又FH=HC,
∴AF/AC=1/7.
答案:1/7
如下图,在△ABC中,D为BC的中点,E为
AD上一点,延长BE交AC于点F,若
AE/AD=1/4,则AF/AC的值为 =______。
点评:在几何证明中,如果题目给的
条件较为分散,可以通过添加辅助线,使
分散的条件适当集中.如果能熟练掌握几个
基本图形,把所要证明的图形转化为基本
图形,可使证明思路更明确,更快捷.
题型二 直角三角形射影定理及应用
已知,如图,在梯形ABCD中,
AD∥BC,AC⊥BD,垂足为E,∠ABC=45°,过
E作AD的垂线交AD于F,
交BC于G,过E作AD的平
行线交AB于H.
求证:FG2=AF·DF+BG·CG+AH·BH.
题型二 直角三角形射影定理及应用
例2.
分析:由射影定理可知AF·DF=EF2,
BG·CG=EG2,故考虑将FG=FE+EG,然后只需
寻找EF·EG与AH·BH的关系.
分析:由射影定理可知AF·DF=EF2,
BG·CG=EG2,故考虑将FG=FE+EG,然后只需
寻找EF·EG与AH·BH的关系.
解析:因为AC⊥BD,故△AED、
△BEC都是直角三角形.
又EF⊥AD,EG⊥BC,由射
影定理可知AF·DF=EF2,
BG·CG=EG2.
点评:做平面几何证明题时要分析待证
明的结论与已知条件的关系,逐步消除差距.
如图,在Rt△ABC中,
∠BAC=90°,AD⊥BC
于D,DF⊥AC于F,DE⊥AB于E,求证:
AD3=BC·BE·CF.
如图,在Rt△ABC中,
∠BAC=90°,AD⊥BC
于D,DF⊥AC于F,DE⊥AB于E,求证:
AD3=BC·BE·CF.
分析:问题题设中含有直角三角形和斜边
上的高,符合直角三角形射影定理的两个条件
中,故考虑应用射影定理求解.
证明:
题型三 相似三角形判定定理及性质定理的应用
题型三 相似三角形判定定理及性质定理的应用
例3.
分析:要证明这四个三角形都相似,可以逐
次证明其中的三角形相似,由于这些三角形都是
直角三角形,因此只要证明两个三角形有一组锐
角相等或两组对应边
成比例即可.
分析:要证明这四个三角形都相似,可以逐
次证明其中的三角形相似,由于这些三角形都是
直角三角形,因此只要证明两个三角形有一组锐
角相等或两组对应边
成比例即可.
解析:
如右图所示,在△ABC中,AB=AC,AD是边BC的中线,P为
AD上一点,CF∥AB,BP的延长线分别交AC,CF于点E,F,
求证:BP2=PE·PF. ?
如右图所示,在△ABC中,AB=AC,AD是边BC的中线,P为
AD上一点,CF∥AB,BP的延长线分别交AC,CF于点E,F,
求证:BP2=PE·PF. ?
方法提炼
1.相似三角形的证法:①定义法:对应
边成比例,对应角相等;②平行法;③判定
定理法;④对直角三角形除以上方法外,还
有特殊方法,两直角边对应成比例,两直角
三角形相似;一条直角边和斜边对应成比
例,两直角三角形相似;斜边上的高分成的
两直角三角形与原三角形相似.
2.相似三角形的性质:①对应边成比例,
对应角相等;②对应高的比、对应中线的比、
对应角平分线的比、周长的比都等于相似比,
而面积的比等于相似比的平方;③相似三角形
外接圆的直径比、周长比等于相似比,外接圆
的面积比等于相似比的平方.利用这些关系可以
进行各种证明、求值.
3.在探究证明中,掌握从特殊到一般和化归
的思想方法,学会解决问题的程序、模式.
走进高考
(2009·江苏卷)如图,在四边
形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
走进高考
(2009·江苏卷)如图,在四边
形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
证明:由△ABC≌△BAD,得∠ACB=∠BDA,
故A、B、C、D四点共圆,从而∠CAB=∠CDB.
再由△ABC≌△BAD,得∠CAB=∠DBA.
因此∠DBA=∠CDB,所以AB∥CD.
练习讲评
同课章节目录
