第1章 三角形的初步认识单元提高测试卷(含解析)
文档属性
| 名称 | 第1章 三角形的初步认识单元提高测试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021浙教版八年级数学上册第1章三角形的初步认识单元提高测试卷
一、选择题(共10题;共30分)
1.有4根小木棒,长度分别为2cm、3cm、4cm、5cm,任意取3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为(??
)
A.?1个?????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.下列命题中,是真命题的是(???
)
A.?互补的角是邻补角????????B.?相等的角是对顶角????????C.?同旁内角互补????????D.?两直线平行,内错角相等
3.如图,把△ABC纸片的∠A沿DE折叠,点A落在四边形CBDE外,则∠1、∠2与∠A的关系是(??
)
A.?∠1+∠2=2∠A???????????
?B.?∠2﹣∠A=2∠1?????????????
??C.?∠2﹣∠1=2∠A???????????????D.?∠1+∠A=
∠2
4.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
的依据是(?????
)
A.?SSS?????????????????????B.?ASA??????????????????????C.?AAS??????????????????????????????D.?以上都不对
5.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是(???
)
A.?1个????????????????????????B.?2个??????????????????????C.?3个???????????????????????????????D.?4个
6.现要在一块三角形的草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(????
)
A.?△ABC的三条中线的交点????????????????????????????B.?△ABC三边的垂直平分线的交点
C.?△ABC三条角平分线的交点?????????????????????????D.?△ABC三条高所在直线的交点
7.如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
A.?∠ABC=∠DCB????????????????????B.?∠ABD=∠DCA?????????????????
?C.?AC=DB?????????????????????
D.?AB=DC
8.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是(???
)
A.?10°???????????????????????????????????????B.?12°???????????????????????????????????????C.?15°???????????????????????????????????????D.?18°
9.如图,在△ABC中,AB的垂直平分线交AC于点D
,
交AB于点E
,
如果
?cm,?
?cm,那么△
的周长是(??????
)
A.?6
cm??????????????????????????????????B.?7
cm??????????????????????????????????C.?8
cm?????????????????????????????????D.?9
cm
10.如图,△ABE,△ADC是△ABC分别沿着边AB,AC翻折形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠BFC的度数为(???
)
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?30°???????????????????????????????????????D.?36°
二、填空题(共6题;共18分)
11.如图,AB∥CD,EF分别与AB,CD交于点B,F,若∠E=30°,∠EFC=130°,则∠A=________。
12.在△ABC中,如果∠A∶∠B∶∠C=1∶2∶3,根据三角形按角进行分类,这个三角形是________三角形.
13.如图,已知∠1=∠2,∠3=∠4,∠A=100°,则x=________。
14.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,若△ABC的面积为21cm2
,
AB=8cm,AC=6cm,则DE的长为________cm.
15.将命题“同角的余角相等”,改写成“如果…,那么…”的形式________.
16.如图,△ABC的面积为49cm2
,
AE=ED,BD=3DC,则图中△AEF的面积等于________.
三、解答题(共7题;共52分)
17.如图,在
和
中,点
、
、
、
在同一直线上,请你从以下4个等式中选出3个作为已知条件,余下的1个作为结论,并说明结论正确的理由(写出各种可能的情况,并选择其中一种说理).
①
;②
;③
;④
.
18.如图,已知△ABC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以说明.
19.如图,在△ABC中,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)求证:∠EFA=90°-
∠B;
(2)若∠B=60°,求证:EF=DF.
20.如图1,AB与CD相交于点O,若∠D=38°,∠B=28°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)∠P的度数;
(2)设∠D=α,∠B=β,∠DAP=
∠DAB,∠DCP=
∠DCB,其他条件不变,如图2,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),直接写出结论.
21.课堂上,老师在黑板上出了一道题:在同一平面内,若∠AOB=70°,∠BOC=15°24′36″,求∠AOC的度数.
下面是八年级同学小明在黑板上写的解题过程:
解:根据题意可画出图(如图1)
因为∠AOB=70°,∠BOC=15°24′36″,
所以∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″
即得到∠AOC=85°24′36″
同学们在下面议论,都说小明解答不全面,还有另一种情况.请按下列要求完成这道题的求解.
(1)依照图1,用尺规作图的方法将另一种解法的图形在图2中补充完整.
(2)结合第(1)小题的图形写出求∠AOC的度数的完整过程.
22.如图
(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示).
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
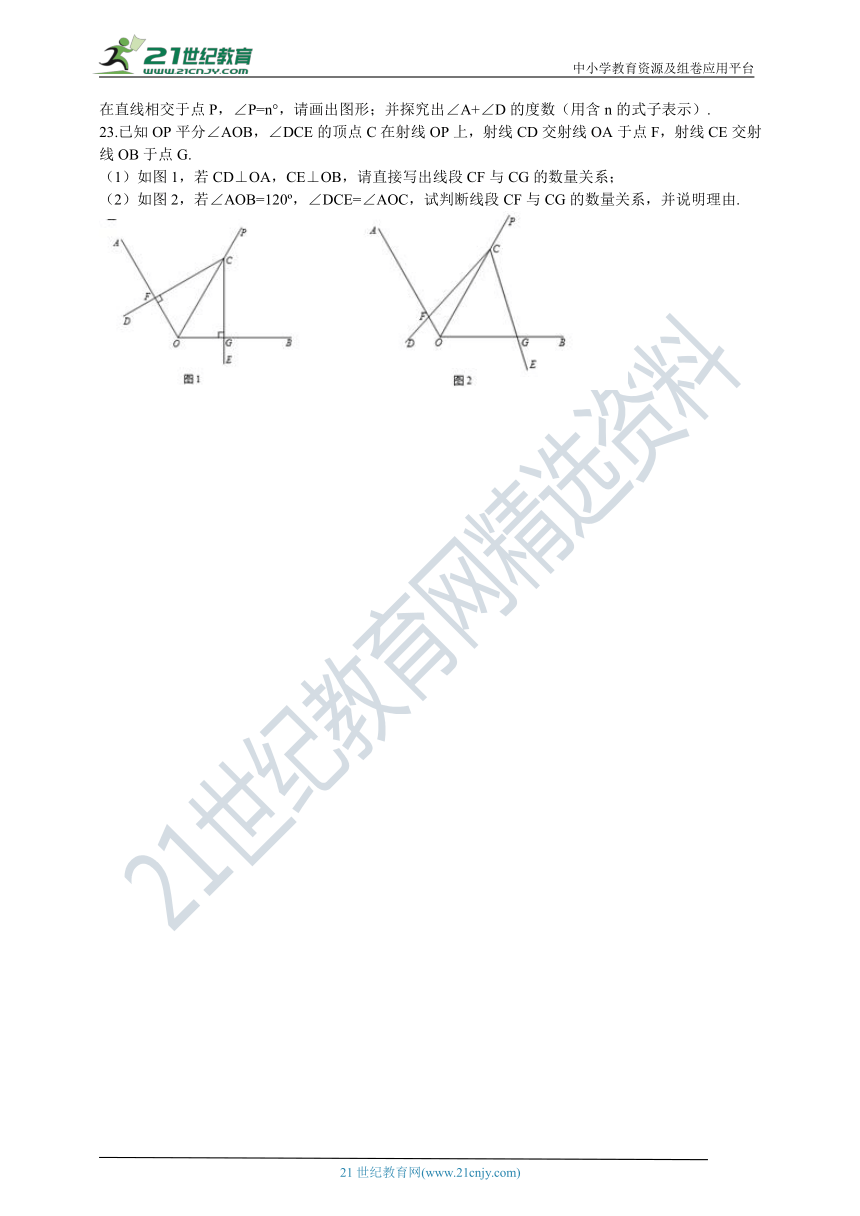
23.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
(2)如图2,若∠AOB=120?,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
答案
1、选择题
1.解:可搭出不同的三角形为:
2cm、3cm、4cm;2cm、4cm、5cm;3cm、4cm、5cm共3个.
故答案为:C.
2.解:互补的角不一定是邻补角,所以A不符合题意,
相等的角不一定是对顶角,所以B不符合题意,
同旁内角不一定互补,所以C不符合题意,
两直线平行,内错角相等,是平行线的性质之一,所以D符合题意.
故答案为:D.
3.解:如图:分别延长CE、BD交于A′点,
而根据折叠可以得到∠EA′A=∠EAA′,∠DA′A=∠DAA′,
∴∠2=∠EA′A+∠EAA′=2∠EAA′,∠1=∠DA′A+∠DAA′=2∠DAA′,
∴∠2﹣∠1=2(∠EAA′﹣∠DAA′)=2∠EAD.
故答案为:C.
4.解:连接NC,MC,
在△ONC和△OMC中
∴△ONC≌△OMC(SSS),
∴∠AOC=∠BOC,
故答案为:A.
5.解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,∠EAF=∠BAC,故①③正确;
∵∠EAF=∠EAB+∠BAF,∠BAC=∠FAC+∠BAF,
∴∠EAB=∠FAC,故④正确;
条件不足,无法证明∠FAB=∠EAB,故②错误;
综上所述,结论正确的是①③④共3个.
故答案为:C.
6.解:∵角平分线上的点到这个角两边的距离相等
∴凉亭的位置应选在△ABC三条角平分线的交点.
故答案为:C.
7A、∵在△ABC和△DCB中
∴△ABC≌△DCB(ASA),故本选项不符合题意;
B、∵∠ABD=∠DCA,∠DBC=∠ACB,
∴∠ABD+∠DBC=∠ACD+∠ACB,
即∠ABC=∠DCB,
∵在△ABC和△DCB中
∴△ABC≌△DCB(ASA),故本选项不符合题意;
C、∵在△ABC和△DCB中
∴△ABC≌△DCB(SAS),故本选项不符合题意;
D、根据∠ACB=∠DBC,BC=BC,AB=DC不能推出△ABC≌△DCB,故本选项符合题意;
故答案为:D.
8.解:
,
,
,
是
的角平分线,
,
,
.
故答案为:B.
9.解:∵AC是AB的垂直平分线
∴AD=BD
∴CD+BD=CD+AD=AC=5
∴△DBC的周长为:CD+BD+BC=AC+BC=5+4=9(cm).
故答案为:D.
10.如图,设AE和DF交于M点,
∵
∠BCA:∠ABC:∠BAC=28:5:3,
∴∠BCA=180°×=140°,
∠ABC=180°×=25°,
∠BAC=180°×=15°,
由折叠的特点可知,∠EAD=3∠BAC=3×15°=45°,∠D=∠ABC=25°,
∠BEA=∠BCA=140°,
∴∠FME=∠AMD=180°-∠D-∠MAD=180°-25°-45°=110°,
∠FEM=180°-∠BCA=180°-140°=40°,
∴∠BFE=180°-∠FME-∠FEM=180°-110°-40°=30°.
故答案为:30°.
二、填空题
11.解:∵AB∥CD
∴∠ABE=∠EFC=130°
∵∠E=30°
∴∠A=180°-130°-30°=20°
故答案为:20°.
12.设三角分别是a,2a,3a
则a+2a+3a=180°
解a=30°
所以三角分别是30°,60°,90°
故这个三角形是直角三角形
故答案:直角
13.解:在△ABC中,∵∠A=100°,
∴∠ABC+∠ACB=180°-∠A=80°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠4=
,
∴
.
故答案为:140°.
14.解:
为
的平分线,
,
,
,
面积
,
即
,
解得
.
故答案为:3.
15.命题“同角的余角相等”,可以改写成:如果两个角是同一个角的余角,那么这两个角相等.
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
16.解:如图:
∵BD=3DC,△ABC的面积为49cm2
,
∴S△ABD=S△ABC=cm2
,
S△ADC=S△ABC=cm2,
∵AE=ED,
∴S△BED=S△ABD=cm2
,
S△AEF=S△EFD
,
∴S△BDF=S△BED+S△AEF=+S△AEF
,
∵BD=3DC,
∴S△FDC=S△BDF=+S△AEF
,
∵S△ADC=S△AEF+S△EFD+S△FDC
,
∴=2S△AEF++S△AEF
,
∴S△AEF=cm2.
故答案为:
.
三、解答题
17.解:已知条件是①,②,④.结论是③.
说理过程:因为
(已知),
所以
(等式性质).即
.
在
和
中,
所以
所以
(全等三角形的对应角相等).
18.
解:△AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM.(任写其中两对即可)
选择△AEM≌△ACN,
∵△ABC≌△ADE,
∴AC=AE,∠C=∠E,∠CAB=∠EAD.
∴∠EAM=∠CAN.
在△AEM和△ACN中,
∴△AEM≌△ACN(ASA).
选择△ABN≌△ADM,
∵△ABC≌△ADE,∴AB=AD,∠B=∠D.
又∵∠BAN=∠DAM,∴△ABN≌△ADM(ASA).
选择△BMF≌△DNF,
∵△ABC≌△ADE,∴AB=AD,∠B=∠D.
又∵∠BAN=∠DAM,∴△ABN≌△ADM(ASA).
∴AN=AM.∴BM=DN.又∵∠B=∠D,∠BFM=∠DFN,∴△BMF≌△DNF(AAS).
(任选一对进行说明即可)
19.
(1)证明:∵∠BAC+∠BCA=180°-∠B,
又∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=
∠BAC,∠FCA=
∠BCA,
∴∠FAC+∠FCA=
×(180°-∠B)=90°-
∠B,
∵∠EFA=∠FAC+∠FCA,
∴∠EFA=90°-
∠B.
(2)证明:如图,过点F作FG⊥BC于G,作FH⊥AB于H,作FM⊥AC于M.
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FM,
∵∠EFH+∠DFH=120°,
∠DFG+∠DFH=360°-90°×2-60°=120°,
∴∠EFH=∠DFG,
在△EFH和△DFG中,
,
∴△EFH≌△DFG(AAS),
∴EF=DF.
20.
(1)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵AP、CP分别为∠DAB和∠BCD的平分线,
∴∠DAO=2∠DAP,∠BCO=2∠DCP,
∴∠DAO-∠BCO=2(∠DAP-∠DCP),
∴∠B-∠D=2(∠P-∠D),
整理得,∠P=
(∠B+∠D),
∵∠D=38°,∠B=28°,
∴∠P=
(38°+28°)=33°
(2)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵∠DAP=
∠DAB,∠DCP=
∠DCB,
∴∠DAO-∠BCO=3(∠DAP-∠DCP),
∴∠B-∠D=3(∠P-∠D),
整理得,∠P=
(∠B+2∠D),
∵∠D=α,∠B=β,
∴∠P=
(β+2α)
21.
(1)解:如图,
(2)解:当OC在∠AOB的外部时,
∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″;
当OC在∠AOB的内部时,
∠AOC=∠AOB-∠BOC
=70°-15°24′36″
=54°35′24″
即得到∠AOC=54°35′24″或85°24′36″.
22.
(1)解:∠A=30°,∠P=15°
∵∠ACD+∠ACB=180°,∠ACD=100°
∴∠ACB=80°,
∵∠ABC+∠ACB+∠A=180°(三角形内角和定理),
又∵∠ABC=70°,
∴∠A=30°,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠PCD=
∠ACD=50°,∠PBC=
∠ABC=35°
∵∠PBC+∠PCB+∠P=180°,∠PCB+∠PCD=180°
∴∠PCD=∠PBC+∠P
∴∠P=50°-35°=15°
(2)解:结论:∠A=2n°,理由如下:
∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC(三角形的一个外角等于与它不相邻的两个内角和),
又∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∴∠A+∠ABC=2(∠P+∠PBC)(等量替换),
∴∠A+∠ABC=2∠P+2∠PBC,
∴∠A+∠ABC=2∠P+∠ABC(等量替换),
∴∠A=2∠P;
∴∠A=2n°
(3)解:(Ⅰ)如图②延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA
=180°﹣(180°﹣∠A)﹣(180°﹣∠D)
=∠A+∠D﹣180°,
由(2)可知:∠F=2∠P=2n°,
∴∠A+∠D=180°+2n°。
(Ⅱ)如图③,延长AB交DC的延长线于F.
∵∠F=180°﹣∠A﹣∠D,∠P=
∠F,
∴∠P=
(180°﹣∠A﹣∠D)=90°﹣
(∠A+∠D).
∴∠A+∠D=180°﹣2n°
综上所述:∠A+∠D=180°+2n°或180°﹣2n°
;
23.
(1)解:结论:CF=CG;
证明:∵OP平分∠AOB,CF⊥OA,CG⊥OB,
∴CF=CG(角平分线上的点到角两边的距离相等);
(2)CF=CG.理由如下:如图,
过点C作CM⊥OA,CN⊥OB,
∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120?,
∴CM=CN(角平分线上的点到角两边的距离相等),
∴∠AOC=∠BOC=60?(角平分线的性质),
∵∠DCE=∠AOC,
∴∠AOC=∠BOC=∠DCE=60?,
∴∠MCO=90?-60?
=30?,∠NCO=90?-60?
=30?,
∴∠MCN=30?+30?=60?,
∴∠MCN=∠DCE,
∵∠MCF=∠MCN-∠DCN,∠NCG=∠DCE-∠DCN,
∴∠MCF=∠NCG,
在△MCF和△NCG中,
∴△MCF≌△NCG(ASA),
∴CF=CG(全等三角形对应边相等);
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021浙教版八年级数学上册第1章三角形的初步认识单元提高测试卷
一、选择题(共10题;共30分)
1.有4根小木棒,长度分别为2cm、3cm、4cm、5cm,任意取3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为(??
)
A.?1个?????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.下列命题中,是真命题的是(???
)
A.?互补的角是邻补角????????B.?相等的角是对顶角????????C.?同旁内角互补????????D.?两直线平行,内错角相等
3.如图,把△ABC纸片的∠A沿DE折叠,点A落在四边形CBDE外,则∠1、∠2与∠A的关系是(??
)
A.?∠1+∠2=2∠A???????????
?B.?∠2﹣∠A=2∠1?????????????
??C.?∠2﹣∠1=2∠A???????????????D.?∠1+∠A=
∠2
4.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
的依据是(?????
)
A.?SSS?????????????????????B.?ASA??????????????????????C.?AAS??????????????????????????????D.?以上都不对
5.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是(???
)
A.?1个????????????????????????B.?2个??????????????????????C.?3个???????????????????????????????D.?4个
6.现要在一块三角形的草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(????
)
A.?△ABC的三条中线的交点????????????????????????????B.?△ABC三边的垂直平分线的交点
C.?△ABC三条角平分线的交点?????????????????????????D.?△ABC三条高所在直线的交点
7.如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
A.?∠ABC=∠DCB????????????????????B.?∠ABD=∠DCA?????????????????
?C.?AC=DB?????????????????????
D.?AB=DC
8.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是(???
)
A.?10°???????????????????????????????????????B.?12°???????????????????????????????????????C.?15°???????????????????????????????????????D.?18°
9.如图,在△ABC中,AB的垂直平分线交AC于点D
,
交AB于点E
,
如果
?cm,?
?cm,那么△
的周长是(??????
)
A.?6
cm??????????????????????????????????B.?7
cm??????????????????????????????????C.?8
cm?????????????????????????????????D.?9
cm
10.如图,△ABE,△ADC是△ABC分别沿着边AB,AC翻折形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠BFC的度数为(???
)
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?30°???????????????????????????????????????D.?36°
二、填空题(共6题;共18分)
11.如图,AB∥CD,EF分别与AB,CD交于点B,F,若∠E=30°,∠EFC=130°,则∠A=________。
12.在△ABC中,如果∠A∶∠B∶∠C=1∶2∶3,根据三角形按角进行分类,这个三角形是________三角形.
13.如图,已知∠1=∠2,∠3=∠4,∠A=100°,则x=________。
14.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,若△ABC的面积为21cm2
,
AB=8cm,AC=6cm,则DE的长为________cm.
15.将命题“同角的余角相等”,改写成“如果…,那么…”的形式________.
16.如图,△ABC的面积为49cm2
,
AE=ED,BD=3DC,则图中△AEF的面积等于________.
三、解答题(共7题;共52分)
17.如图,在
和
中,点
、
、
、
在同一直线上,请你从以下4个等式中选出3个作为已知条件,余下的1个作为结论,并说明结论正确的理由(写出各种可能的情况,并选择其中一种说理).
①
;②
;③
;④
.
18.如图,已知△ABC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以说明.
19.如图,在△ABC中,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)求证:∠EFA=90°-
∠B;
(2)若∠B=60°,求证:EF=DF.
20.如图1,AB与CD相交于点O,若∠D=38°,∠B=28°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)∠P的度数;
(2)设∠D=α,∠B=β,∠DAP=
∠DAB,∠DCP=
∠DCB,其他条件不变,如图2,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),直接写出结论.
21.课堂上,老师在黑板上出了一道题:在同一平面内,若∠AOB=70°,∠BOC=15°24′36″,求∠AOC的度数.
下面是八年级同学小明在黑板上写的解题过程:
解:根据题意可画出图(如图1)
因为∠AOB=70°,∠BOC=15°24′36″,
所以∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″
即得到∠AOC=85°24′36″
同学们在下面议论,都说小明解答不全面,还有另一种情况.请按下列要求完成这道题的求解.
(1)依照图1,用尺规作图的方法将另一种解法的图形在图2中补充完整.
(2)结合第(1)小题的图形写出求∠AOC的度数的完整过程.
22.如图
(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示).
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).
23.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
(2)如图2,若∠AOB=120?,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
答案
1、选择题
1.解:可搭出不同的三角形为:
2cm、3cm、4cm;2cm、4cm、5cm;3cm、4cm、5cm共3个.
故答案为:C.
2.解:互补的角不一定是邻补角,所以A不符合题意,
相等的角不一定是对顶角,所以B不符合题意,
同旁内角不一定互补,所以C不符合题意,
两直线平行,内错角相等,是平行线的性质之一,所以D符合题意.
故答案为:D.
3.解:如图:分别延长CE、BD交于A′点,
而根据折叠可以得到∠EA′A=∠EAA′,∠DA′A=∠DAA′,
∴∠2=∠EA′A+∠EAA′=2∠EAA′,∠1=∠DA′A+∠DAA′=2∠DAA′,
∴∠2﹣∠1=2(∠EAA′﹣∠DAA′)=2∠EAD.
故答案为:C.
4.解:连接NC,MC,
在△ONC和△OMC中
∴△ONC≌△OMC(SSS),
∴∠AOC=∠BOC,
故答案为:A.
5.解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,∠EAF=∠BAC,故①③正确;
∵∠EAF=∠EAB+∠BAF,∠BAC=∠FAC+∠BAF,
∴∠EAB=∠FAC,故④正确;
条件不足,无法证明∠FAB=∠EAB,故②错误;
综上所述,结论正确的是①③④共3个.
故答案为:C.
6.解:∵角平分线上的点到这个角两边的距离相等
∴凉亭的位置应选在△ABC三条角平分线的交点.
故答案为:C.
7A、∵在△ABC和△DCB中
∴△ABC≌△DCB(ASA),故本选项不符合题意;
B、∵∠ABD=∠DCA,∠DBC=∠ACB,
∴∠ABD+∠DBC=∠ACD+∠ACB,
即∠ABC=∠DCB,
∵在△ABC和△DCB中
∴△ABC≌△DCB(ASA),故本选项不符合题意;
C、∵在△ABC和△DCB中
∴△ABC≌△DCB(SAS),故本选项不符合题意;
D、根据∠ACB=∠DBC,BC=BC,AB=DC不能推出△ABC≌△DCB,故本选项符合题意;
故答案为:D.
8.解:
,
,
,
是
的角平分线,
,
,
.
故答案为:B.
9.解:∵AC是AB的垂直平分线
∴AD=BD
∴CD+BD=CD+AD=AC=5
∴△DBC的周长为:CD+BD+BC=AC+BC=5+4=9(cm).
故答案为:D.
10.如图,设AE和DF交于M点,
∵
∠BCA:∠ABC:∠BAC=28:5:3,
∴∠BCA=180°×=140°,
∠ABC=180°×=25°,
∠BAC=180°×=15°,
由折叠的特点可知,∠EAD=3∠BAC=3×15°=45°,∠D=∠ABC=25°,
∠BEA=∠BCA=140°,
∴∠FME=∠AMD=180°-∠D-∠MAD=180°-25°-45°=110°,
∠FEM=180°-∠BCA=180°-140°=40°,
∴∠BFE=180°-∠FME-∠FEM=180°-110°-40°=30°.
故答案为:30°.
二、填空题
11.解:∵AB∥CD
∴∠ABE=∠EFC=130°
∵∠E=30°
∴∠A=180°-130°-30°=20°
故答案为:20°.
12.设三角分别是a,2a,3a
则a+2a+3a=180°
解a=30°
所以三角分别是30°,60°,90°
故这个三角形是直角三角形
故答案:直角
13.解:在△ABC中,∵∠A=100°,
∴∠ABC+∠ACB=180°-∠A=80°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠4=
,
∴
.
故答案为:140°.
14.解:
为
的平分线,
,
,
,
面积
,
即
,
解得
.
故答案为:3.
15.命题“同角的余角相等”,可以改写成:如果两个角是同一个角的余角,那么这两个角相等.
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
16.解:如图:
∵BD=3DC,△ABC的面积为49cm2
,
∴S△ABD=S△ABC=cm2
,
S△ADC=S△ABC=cm2,
∵AE=ED,
∴S△BED=S△ABD=cm2
,
S△AEF=S△EFD
,
∴S△BDF=S△BED+S△AEF=+S△AEF
,
∵BD=3DC,
∴S△FDC=S△BDF=+S△AEF
,
∵S△ADC=S△AEF+S△EFD+S△FDC
,
∴=2S△AEF++S△AEF
,
∴S△AEF=cm2.
故答案为:
.
三、解答题
17.解:已知条件是①,②,④.结论是③.
说理过程:因为
(已知),
所以
(等式性质).即
.
在
和
中,
所以
所以
(全等三角形的对应角相等).
18.
解:△AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM.(任写其中两对即可)
选择△AEM≌△ACN,
∵△ABC≌△ADE,
∴AC=AE,∠C=∠E,∠CAB=∠EAD.
∴∠EAM=∠CAN.
在△AEM和△ACN中,
∴△AEM≌△ACN(ASA).
选择△ABN≌△ADM,
∵△ABC≌△ADE,∴AB=AD,∠B=∠D.
又∵∠BAN=∠DAM,∴△ABN≌△ADM(ASA).
选择△BMF≌△DNF,
∵△ABC≌△ADE,∴AB=AD,∠B=∠D.
又∵∠BAN=∠DAM,∴△ABN≌△ADM(ASA).
∴AN=AM.∴BM=DN.又∵∠B=∠D,∠BFM=∠DFN,∴△BMF≌△DNF(AAS).
(任选一对进行说明即可)
19.
(1)证明:∵∠BAC+∠BCA=180°-∠B,
又∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=
∠BAC,∠FCA=
∠BCA,
∴∠FAC+∠FCA=
×(180°-∠B)=90°-
∠B,
∵∠EFA=∠FAC+∠FCA,
∴∠EFA=90°-
∠B.
(2)证明:如图,过点F作FG⊥BC于G,作FH⊥AB于H,作FM⊥AC于M.
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FM,
∵∠EFH+∠DFH=120°,
∠DFG+∠DFH=360°-90°×2-60°=120°,
∴∠EFH=∠DFG,
在△EFH和△DFG中,
,
∴△EFH≌△DFG(AAS),
∴EF=DF.
20.
(1)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵AP、CP分别为∠DAB和∠BCD的平分线,
∴∠DAO=2∠DAP,∠BCO=2∠DCP,
∴∠DAO-∠BCO=2(∠DAP-∠DCP),
∴∠B-∠D=2(∠P-∠D),
整理得,∠P=
(∠B+∠D),
∵∠D=38°,∠B=28°,
∴∠P=
(38°+28°)=33°
(2)解:根据三角形的内角和定理,∠DAP+∠D=∠DCP+∠P,
∴∠DAP-∠DCP=∠P-∠D,
∠DAO+∠D=∠BCO+∠B,
∴∠DAO-∠BCO=∠B-∠D,
∵∠DAP=
∠DAB,∠DCP=
∠DCB,
∴∠DAO-∠BCO=3(∠DAP-∠DCP),
∴∠B-∠D=3(∠P-∠D),
整理得,∠P=
(∠B+2∠D),
∵∠D=α,∠B=β,
∴∠P=
(β+2α)
21.
(1)解:如图,
(2)解:当OC在∠AOB的外部时,
∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″;
当OC在∠AOB的内部时,
∠AOC=∠AOB-∠BOC
=70°-15°24′36″
=54°35′24″
即得到∠AOC=54°35′24″或85°24′36″.
22.
(1)解:∠A=30°,∠P=15°
∵∠ACD+∠ACB=180°,∠ACD=100°
∴∠ACB=80°,
∵∠ABC+∠ACB+∠A=180°(三角形内角和定理),
又∵∠ABC=70°,
∴∠A=30°,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠PCD=
∠ACD=50°,∠PBC=
∠ABC=35°
∵∠PBC+∠PCB+∠P=180°,∠PCB+∠PCD=180°
∴∠PCD=∠PBC+∠P
∴∠P=50°-35°=15°
(2)解:结论:∠A=2n°,理由如下:
∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC(三角形的一个外角等于与它不相邻的两个内角和),
又∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∴∠A+∠ABC=2(∠P+∠PBC)(等量替换),
∴∠A+∠ABC=2∠P+2∠PBC,
∴∠A+∠ABC=2∠P+∠ABC(等量替换),
∴∠A=2∠P;
∴∠A=2n°
(3)解:(Ⅰ)如图②延长BA交CD的延长线于F.
∵∠F=180°﹣∠FAD﹣∠FDA
=180°﹣(180°﹣∠A)﹣(180°﹣∠D)
=∠A+∠D﹣180°,
由(2)可知:∠F=2∠P=2n°,
∴∠A+∠D=180°+2n°。
(Ⅱ)如图③,延长AB交DC的延长线于F.
∵∠F=180°﹣∠A﹣∠D,∠P=
∠F,
∴∠P=
(180°﹣∠A﹣∠D)=90°﹣
(∠A+∠D).
∴∠A+∠D=180°﹣2n°
综上所述:∠A+∠D=180°+2n°或180°﹣2n°
;
23.
(1)解:结论:CF=CG;
证明:∵OP平分∠AOB,CF⊥OA,CG⊥OB,
∴CF=CG(角平分线上的点到角两边的距离相等);
(2)CF=CG.理由如下:如图,
过点C作CM⊥OA,CN⊥OB,
∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120?,
∴CM=CN(角平分线上的点到角两边的距离相等),
∴∠AOC=∠BOC=60?(角平分线的性质),
∵∠DCE=∠AOC,
∴∠AOC=∠BOC=∠DCE=60?,
∴∠MCO=90?-60?
=30?,∠NCO=90?-60?
=30?,
∴∠MCN=30?+30?=60?,
∴∠MCN=∠DCE,
∵∠MCF=∠MCN-∠DCN,∠NCG=∠DCE-∠DCN,
∴∠MCF=∠NCG,
在△MCF和△NCG中,
∴△MCF≌△NCG(ASA),
∴CF=CG(全等三角形对应边相等);
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
