1.4 全等三角形同步训练（含解析）

中小学教育资源及组卷应用平台
初中数学浙教版八年级上册1.4 全等三角形 同步训练
一、单选题
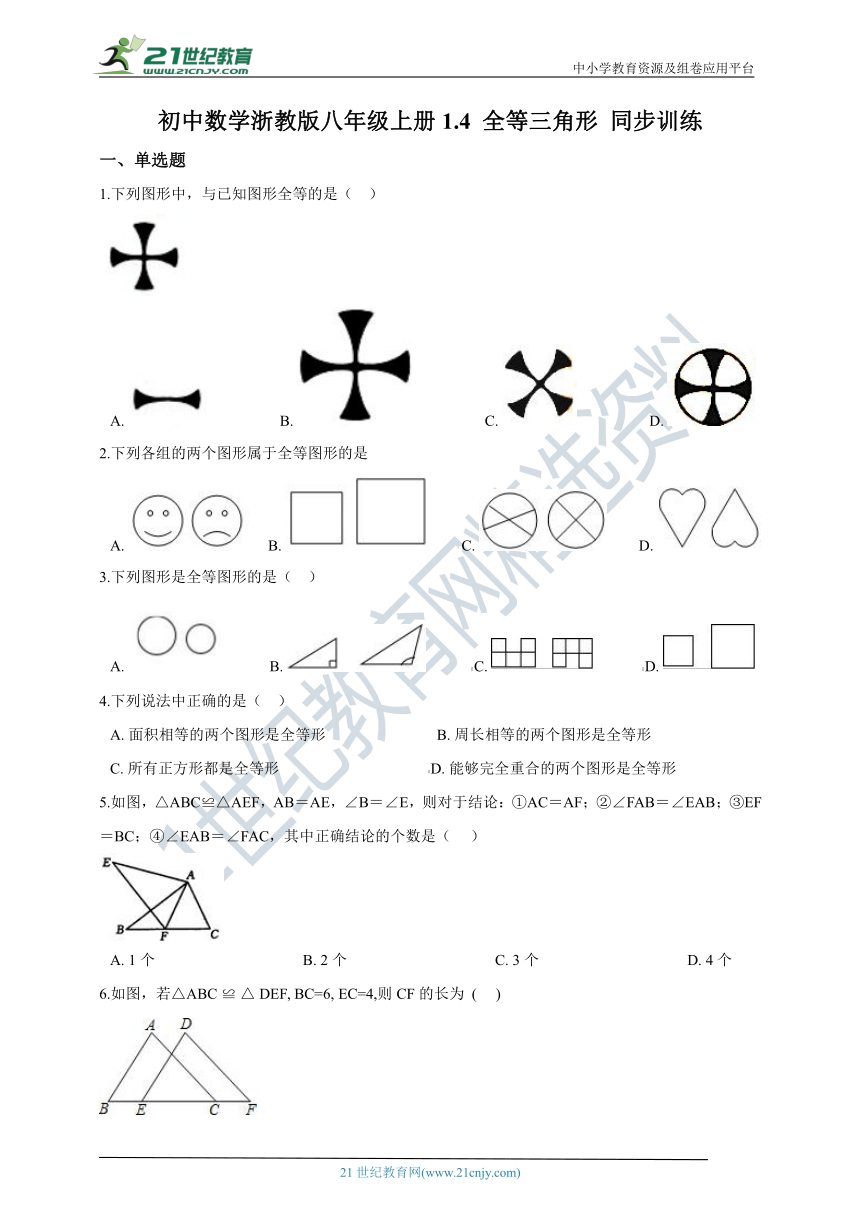
1.下列图形中，与已知图形全等的是（?? ）

A.????????????????????B.????????????????????C.????????????????????D.?
2.下列各组的两个图形属于全等图形的是
A.??????B.?????????C.?????????D.?
3.下列图形是全等图形的是（?? ）
A.????????? B.?????????????C.?????????????D.?
4.下列说法中正确的是（?? ）
A.?面积相等的两个图形是全等形?????????????????????????????B.?周长相等的两个图形是全等形
C.?所有正方形都是全等形???????????????????????????????????????D.?能够完全重合的两个图形是全等形
5.如图，△ABC≌△AEF，AB＝AE，∠B＝∠E，则对于结论：①AC＝AF；②∠FAB＝∠EAB；③EF＝BC；④∠EAB＝∠FAC，其中正确结论的个数是（??? ）
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
6.如图，若△ABC ≌ △ DEF, BC=6, EC=4,则CF的长为 (??? )
A.?1??????????????????????????????????????????B.?2??????????????????????????????????????????C.?2.5??????????????????????????????????????????D.?3
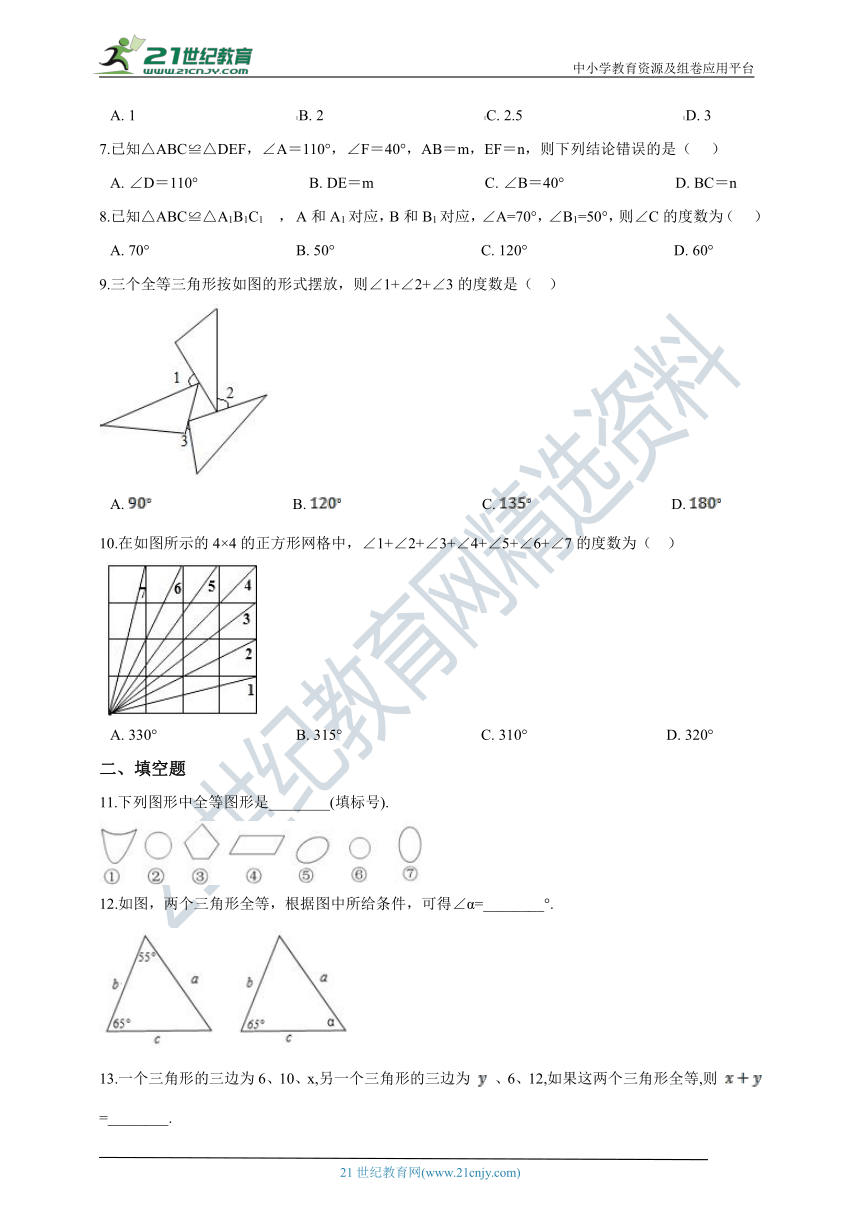
7.已知△ABC≌△DEF，∠A＝110°，∠F＝40°，AB＝m，EF＝n，则下列结论错误的是（??? ）
A.?∠D＝110°?????????????????????????????B.?DE＝m?????????????????????????????C.?∠B＝40°?????????????????????????????D.?BC＝n
8.已知△ABC≌△A1B1C1 ， A和A1对应，B和B1对应，∠A=70°，∠B1=50°，则∠C的度数为（ ???）
A.?70°??????????????????????????????????????B.?50°??????????????????????????????????????C.?120°??????????????????????????????????????D.?60°
9.三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数是（?? ）
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
10.在如图所示的4×4的正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为（?? ）

A.?330°????????????????????????????????????B.?315°????????????????????????????????????C.?310°????????????????????????????????????D.?320°
二、填空题
11.下列图形中全等图形是________(填标号).
12.如图，两个三角形全等，根据图中所给条件，可得∠α=________°.
13.一个三角形的三边为6、10、x,另一个三角形的三边为 、6、12,如果这两个三角形全等,则 =________.
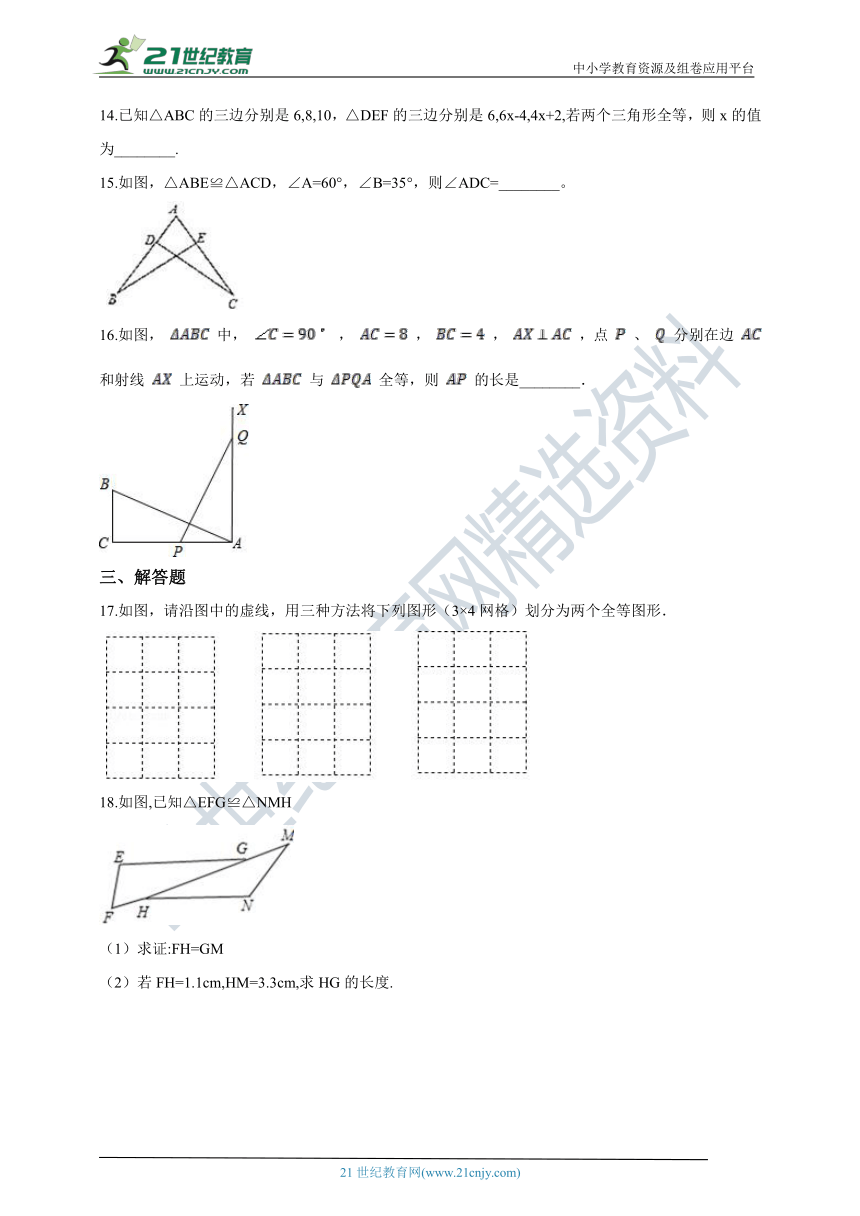
14.已知△ABC的三边分别是6,8,10，△DEF的三边分别是6,6x-4,4x+2,若两个三角形全等，则x的值为________.
15.如图，△ABE≌△ACD，∠A=60°，∠B=35°，则∠ADC=________。

16.如图， 中， ， ， ， ，点 、 分别在边 和射线 上运动，若 与 全等，则 的长是________．
三、解答题
17.如图，请沿图中的虚线，用三种方法将下列图形（3×4网格）划分为两个全等图形．

18.如图,已知△EFG≌△NMH
（1）求证:FH=GM
（2）若FH=1.1cm,HM=3.3cm,求HG的长度.
答案解析部分
一、单选题
1. C
考点：全等图形
解：由已知图形可得： 与 全等，
故答案为：C．
分析：能够完全重合的两个图形全等。根据定义即可判断求解。
2. D
考点：全等图形
解：A、两只眼睛下面的嘴巴不能完全重合，故本选项错误；
B、两个正方形的边长不相等，不能完全重合，故本选项错误；
C、圆内两条相交的线段不能完全重合，故本选项错误；
D、两个图形能够完全重合，故本选项正确.
故答案为：D.
分析：能够完全重合的两个图形就是全等形，根据定义一一判断即可.
3. C
考点：全等图形
解：A、两个圆不一样大，不是全等图形，不符合题意；
B、两个三角形最大角分别是直角和钝角，不符合题意；
C、两个图形放置的方位不一致，但图形的大小一样，形状相同，是全等图形，符合题意；
D、两个正方形的大小不一样，不是全等图形；
故答案为：C .
分析：只有形状相同，大小相等的两个图形才全等, 据此分别分析和判断.
4. D
考点：全等图形
解：因为能够完全重合的两个图形是全等形，所以选D.
分析：全等形：能够完全重合的两个图形是全等形。
5. C
考点：全等三角形的性质
解：∵△ABC≌△AEF，
∴AC＝AF，EF＝BC，∠EAF＝∠BAC，故①③正确；
∵∠EAF＝∠EAB＋∠BAF，∠BAC＝∠FAC＋∠BAF，
∴∠EAB＝∠FAC，故④正确；
条件不足，无法证明∠FAB＝∠EAB，故②错误；
综上所述，结论正确的是①③④共3个.
故答案为：C.
分析：根据全等三角形的对应角相等，对应边相等即可一一判断得出答案.
6. B
考点：全等三角形的性质
解：∵△ABC ≌ △ DEF，
∴BC=EF=6，
∴CF= ；
故答案为：B.
分析：根据全等三角形的性质，得到BC=EF，即可求出CF的长度；
7. C
考点：全等三角形的性质
解：:∵△ABC≌△DEF
∴∠D＝∠A＝110°,故A正确;
∵△ABC≌△DEF
∴DE＝AB＝m,故B正确;
∵△ABC≌△DEF
∴∠C＝∠F＝40°
∴∠B=180°－∠A－∠C=30°,故C错误;
∵△ABC≌△DEF
∴BC＝EF＝n, 故D正确;
故答案为：C.
分析：根据全等三角形的对应边相等,对应角也相等逐一判断即可.
8. D
考点：全等三角形的性质
解：∵△ABC≌△A1B1C1 ， A和A1对应，B和B1对应，
∴∠B=∠B1=50°，
∵∠C=180°-∠A-∠B
∴∠C=180°-70°-50°=60°.
故答案为：D.
分析：利用全等三角形的对应角相等，可求出∠B的度数，然后利用三角形内角和等于180°，就可求出∠C的度数。
9. D
考点：三角形内角和定理，三角形的外角性质，全等三角形的性质
解：如图，
∵图中是三个全等三角形，
∴∠4=∠8,∠6=∠7,
又∵三角形ABC的外角和=∠1+∠2+∠3+∠4+∠5+∠6=360?,
又∠5+∠7+∠8=180°，
∴∠1+∠2+∠3=360°-180°=180°.
故答案为：D
分析：根据全等三角形的对应角相等可得∠4=∠8,∠6=∠7,由三角形ABC的外角和=∠1+∠2+∠3+∠4+∠5+∠6及三角形的内角和∠5+∠7+∠8=180°，即可求出答案.
10. B
考点：全等三角形的性质
解：由图可知，∠1所在的三角形与∠7所在的三角形全等，
所以∠1+∠7=90°．
同理得，∠2+∠6=90°，∠3+∠5=90°．
又∠4=45°，
所以∠1+∠2+∠3+∠4+∠5+∠6+∠7=315°．
故答案为：B．
分析：由三角形全等的判定边角边可知，∠1所在的三角形与∠7所在的三角形全等，∠2所在的三角形与∠6所在的三角形全等，∠3所在的三角形与∠5所在的三角形全等，再根据直角三角形两锐角互余即可求解。
二、填空题
11. ⑤和⑦
考点：全等图形
解：由全等形的概念可知：共有1对图形全等，即⑤和⑦能够重合，故答案为⑤和⑦.
分析：能够完全重合的两个图形是全等图形，据此逐一判断即可.
12. 60
考点：三角形内角和定理，全等三角形的性质
解：∵两个三角形全等
∴
故答案为：60.
分析：根据全等三角形的性质和三角形内角和定理求解即可.
13. 22
考点：全等三角形的性质
解：∵一个三角形的三边为6、10、x,另一个三角形的三边为 、6、12,且两个三角形全等
∴y=10,x=12，
∴x+y=22,
故填：22.
分析：根据全等三角形的对应边相等可求得x、y，再求和即可求解.
14. 2
考点：全等三角形的性质
解：依题意①8=6x-4,和10=4x+2
分别解得x=2，x=2，
故x=2；
②8=4x+2，10=6x-4
分别解得x= ,x=
综上：x=2,
故答案为：2.
分析：根据全等三角形的对应边相等，分两种情况列出方程，求解并检验即可得出答案.
15. 85°
考点：三角形内角和定理，全等三角形的性质
解：∵∠AEB=180°-(∠A+∠B)=180°-(60°+35°)=85°，
∵ △ABE≌△ACD，
∴∠ADC=∠AEB=85°.
故答案为：85°.
分析：由三角和内角和定理求出∠AEB的度数，然后根据全等三角形对应角相等即可求出∠ADC的度数.
16. 4或8
考点：全等三角形的性质
解： ∵△ABC与△PQA全等，
∴AP=BC=4或AP=AC=8，
故AP的长为4或8.
分析：根据已知可得∠C=∠PAQ=90°，则点A与点C为对应点，由于△ABC与△PQA全等，则需分AP=BC或AP=AC两种情况讨论.
三、解答题
17. 解：如图
考点：全等图形
分析：利用全等三角形的定义进行分析画出图形即可。
18. （1）证明：∵△EFG≌△NMH,
∴FG=MH,
∴FG-HG=MH-HG
∴FH=GM
（2）解：∵EF=MN,EF=2.1cm,
∴MN=2.1cm；
∵FG=MH,FH+HG=FG,FH=1.1cm,HM=3.3cm,
∴HG=FG-FH=HM-FH=3.3-1.1=2.2cm
考点：全等三角形的性质
分析：（1）由全等三角形的性质可得FG=MH, 再由线段的构成可求解；
（2）由全等三角形的性质可得EF=MN，FG=MH，根据 HG=FG-FH=HM-FH可求解.
_21?????????è?????(www.21cnjy.com)_