1.3 证明同步训练（含解析）

中小学教育资源及组卷应用平台
初中数学浙教版八年级上册1.3 证明 同步训练
一、单选题
1.以下判断正确的是（??? ）
A.?三角形的一个外角等于两个内角的和??????????????????B.?三角形的外角大于任何一个内角
C.?一个三角形中，至少有一个角大于或等于60°??????D.?三角形的外角是内角的邻补角
2.如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2=44°，则∠1的大小为(??? )

A.?14°????????????????????????????????????B.?16°????????????????????????????????????C.?90°-α????????????????????????????????????D.?α-44°
3.AD是∠CAE的平分线，∠B＝35°，∠DAE＝60°，则∠ACD= ( ??????)
A.?25°???????????????????????????????????????B.?60°???????????????????????????????????????C.?85°???????????????????????????????????????D.?95°
4.已知， ，判断 之间的关系满足（? ）
A.??????????????????????????????????????B.?
C.???????????????????????????????????????D.?
5.如图所示，两条直线AB、CD被第三条直线EF所截，∠1=75°，下列说法正确的（? ）
A.?若∠4=75°，则AB∥CD???????????????????????????????????????B.?若∠4=105°，则AB∥CD
C.?若∠2=75°，则AB∥CD???????????????????????????????????????D.?若∠2=155°，则AB∥CD
6.下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容。
已知：如图，∠BEC=∠B+∠C
求证：AB∥CD
证明：延长BE交※于点F，
则∠BEC=180°-∠FEC=◎+∠C
又∠BEC=∠B+∠C，得∠B=▲
故AB∥CD(@相等，两直线平行)

则回答正确的是(??? )
A.?◎代表∠FEC??????????????????????B.?@代表同位角??????????????????????C.?▲代表∠EFC??????????????????????D.?※代表AB
二、填空题
7.如图所示，边长为1正方形网格中，点A、B、C落在格点上，则 的度数为________．
8.小明在玩“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题，如图，若AB∥CD，∠BAE=92°，∠DCE=121°，则∠AEC=________°。

9.一个零件的形状如图所示，按规定∠A应等于90°，∠B、∠C应分别是21°和32°．当检验工人量得的∠BDC的度数不等于________度时，就可判定此零件不合格？???
???
10.如图，给出下列三个论断：①∠B+∠D=180°；②AB∥CD；③BC∥DE．请你以其中两个论断作为已知条件，填入“已知”栏中，以一个论断作为结论，填入“结论栏中，使之成为一道由已知可得到结论的题目，并说明理由．
已知，如图， ________ ，
结论： ________ ．
理由： ________ ．
11.如图，在 中， ， 和 的平分线交于点 ，得 ； 和 的平分线交于点 ，得 和 的平分线交于点 ，则 ________度.
12.请在括号内填写下列证明过程的依据：已知：如图，在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC 的平分线。
求证：∠A=2∠H
证明：∵∠ACD是∠ABC的一个外角，
∴∠ACD=∠ABC+∠A
________
∠2是△BCH的一个外角，
∠2=∠1+∠H（理由同上）
∵CH是外角∠ACD的平分线，BH是∠ABC的平分线
∴∠1= ∠ABC，∠2= ∠ACD ________
∴∠A=∠ACD-∠ABC=2（∠2-∠1） （等式的性质）
而∠H=∠2-∠1 （等式的性质）
∴∠A=2∠H________
三、解答题
13.如图，点D、E在AB上点F在BC上，点G在AC上，∠1=∠B，∠2=∠3，∠4=80°，求∠ADC的度数.
14.已知：如图，在△ABC中，AD∥BC，AD平分外角∠EAC，求证：∠B=∠C．

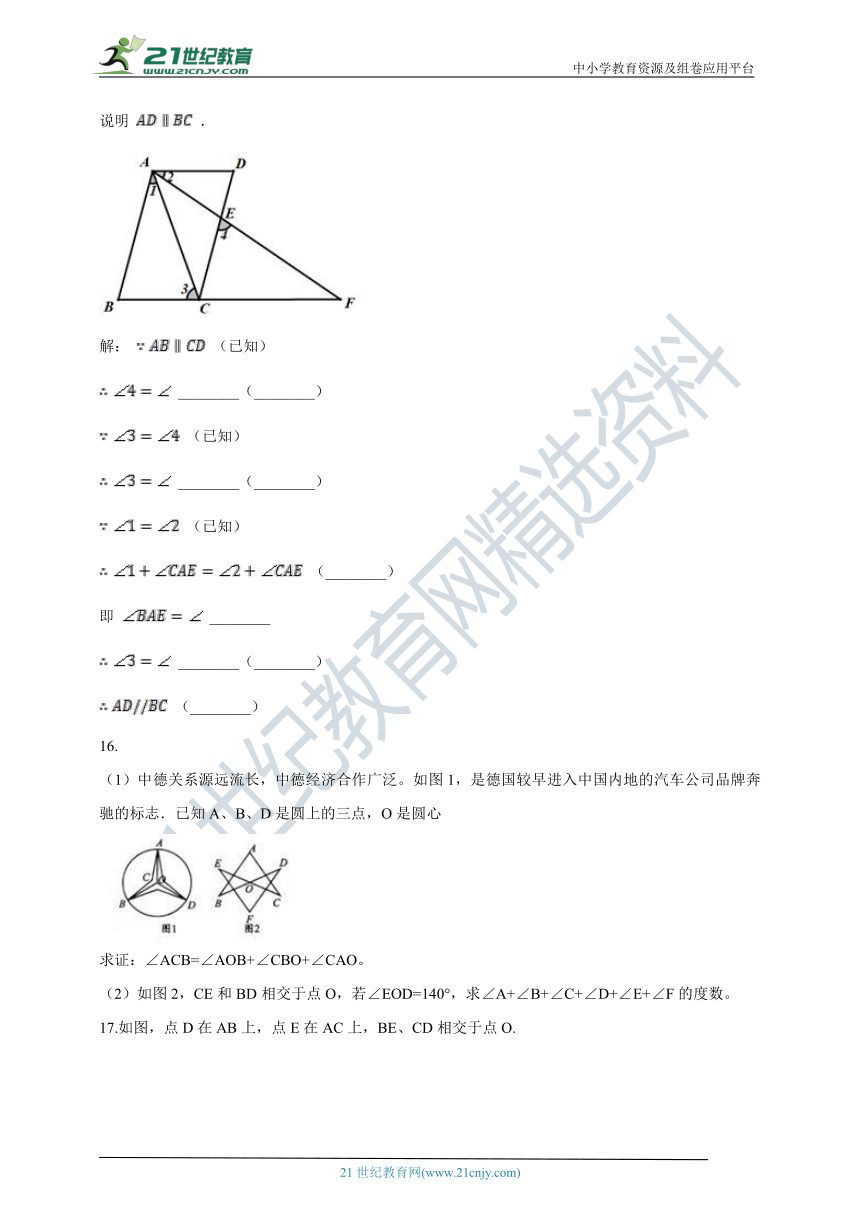
15.阅读并填空．已知：如图，线 、线 是直线， ．试说明 ．
解： （已知）
________（________）
（已知）
________（________）
（已知）
（________）
即 ________
________（________）
（________）
16.?????????????
（1）中德关系源远流长，中德经济合作广泛。如图1，是德国较早进入中国内地的汽车公司品牌奔驰的标志．已知A、B、D是圆上的三点，O是圆心

求证：∠ACB=∠AOB+∠CBO+∠CAO。
（2）如图2，CE和BD相交于点O，若∠EOD=140°，求∠A+∠B+∠C+∠D+∠E+∠F的度数。
17.如图，点D在AB上，点E在AC上，BE、CD相交于点O.
（1）若∠A=50°，∠BOD=70°，∠C=30°，求∠B的度数；
（2）试猜想∠BOC与∠A+∠B+∠C之间的关系，并证明你猜想的正确性.
18.在△ABC中，AE⊥BC于点E，∠BAE：∠CAE＝4：6，BD平分∠ABC，点F在BC上，∠CDF＝60°，∠ABD＝25°.
（1）求∠CAE的度数；
（2）求证：DF⊥BC.
答案解析部分
一、单选题
1. C
考点：三角形内角和定理，三角形的外角性质，三角形相关概念
解：A．应为三角形的一个外角等于与它不相邻的两个内角的和，故本选项不符合题意；
B．应为三角形的外角大于任何一个与它不相邻的内角，故本选项不符合题意；
C．根据三角形的内角和定理，若三个内角都小于60°，则内角和小于180°，所以一个三角形中，至少有一个角大于或等于60°，故本选项符合题意；
D．应为三角形的外角是相邻内角的邻补角，故本选项不符合题意．
故答案为：C
分析：根据三角形的一个外角等于与它不相邻的两个内角的和的性质，三角形的外角大于任何一个与它不相邻的内角，三角形的内角和定理，三角形的外角是相邻内角的邻补角，对各选项分析判断后利用排除法
2. A
考点：平行线的性质，三角形的外角性质
解：如图：
∵AD∥BC，
∴∠3=∠2=44°，
∵∠3=∠1+30°，
∴∠1=14°.

故答案为：A.
分析：根据平行线的性质得∠3=∠2=44°，由三角形外角性质得∠3=∠1+30°，即可求出∠1=14°.
3. D
考点：三角形的外角性质
解：∵AD是∠CAE的平分线，
∴∠EAC=2∠DAE=120°，
∴∠ACB=∠EAC-∠B=120°-35°=85°，
∴∠ACD=180°-∠ACB=95°.
故答案为：D.
分析：根据角平分线的定义得到∠EAC=2∠DAE=120°，根据三角形的外角的性质计算即可.
4. C
考点：平行线的性质，三角形的外角性质
解：延长CD，DC，分别交EF，AB于点G，H
∵
∴∠1+∠4=90°
∴∠1+∠4+∠2=90°+∠3+∠5
∵
∴∠4=∠5
∴∠1+∠2=90°+∠3
即
故答案为：C
分析：延长CD，DC，分别交EF，AB于点G，H，已知 ，可知∠1+∠4=90°，已知 ，可得，且∠2=∠3+∠5，即可求解．
5.B
考点：平行线的判定，推理与论证
解：答：解：A、∵∠4=75°，
∴∠3=180°-75°=105°，
∴∠1≠∠3，
∴AB、CD不平行，
故不符合题意；
B、∵∠4=105°，
∴∠3=180°-105°=75°，
∴∠1=∠3，
∴AB、CD平行，
故符合题意；
C、∵∠2=75°，
∴∠1=∠2，
又∵∠1、∠2是对顶角，
∴AB、CD不平行，
故不符合题意；
D、∵∠2=155°，
∴∠1≠∠2，
又∵∠1、∠2是对顶角，
∴∠1=∠2，
故此题矛盾，而AB、CD更不可能不平行，
故不符合题意．
故答案为：B．
分析：（1）由邻补角的性质可得∠3=180°-75°=105°≠∠1，同位角不相等，不能判断两直线平行；
（2）由邻补角的性质可得∠3=180°-105°=75°=∠1，根据同位角相等，两直线平行可求解；
（3）由已知可得∠1=∠2，对顶角相等，不能判断两直线平行；
（4）由对顶角相等可得对顶角相等，与已知∠1≠∠2矛盾，不能判断两直线平行。
6. C
考点：平行线的判定，三角形的外角性质
解：证明：延长BE交CD于点F，则
∠BEC＝∠EFC＋∠C．
又∵∠BEC＝∠B＋∠C，
∴∠B＝∠EFC，
∴AB∥CD（内错角相等，两直线平行）．
∴※代表CD，⊙代表∠EFC，▲代表∠EFC，□代表内错角．
故答案为：C．
分析：延长BE交CD于点F，利用三角形外角的性质可得出∠BEC＝∠EFC＋∠C，结合∠BEC＝∠B＋∠C可得出∠B＝∠EFC，利用“内错角相等，两直线平行”可证出AB∥CD，找出各符号代表的含义，再对照四个选项即可得出结论．
二、填空题
7. 45°
考点：三角形的外角性质，图形的剪拼
解：过C作CD AB交BA的延长线于 D，则D刚好在格点上，
?边长为1正方形，
? ?
是 的外角，
?
故答案为：
分析：过C作CD AB交BA的延长线于 D，则D刚好在格点上，利用正方形的性质，三角形的外角的性质可得答案．
8. 29
考点：平行线的性质，三角形的外角性质
解：如图，延长DC到E，交AE于点F，
?∵? AB∥CD，
?∴ ∠DFE=∠BAE=92°，
?∵ ∠DCE=∠DFE+∠AEC ,
?∴∠AEC=121° -92°=29?.

?
分析：延长DC到E，交AE于点F，根据平行线的性质得∠DFE=∠BAE，由外角的性质得∠DCE=∠DFE+∠AEC ,即可求出∠AEC的度数.
9.143
考点：三角形内角和定理，三角形的外角性质，推理与论证
解：延长CD交AB于E．∵∠BED=∠A+∠C，∠BDC=∠BED+∠B，∠A=90°，∠B=21°，∠C=32°，
∴∠BDC=∠A+∠C+∠B=90°+21°+32°=143°．
故当检验工人量得∠BDC≠143°时，就可判定此零件不合格．
分析：由题意补全图形，延长CD交AB于E。根据三角形的一个外角等于和它不相邻的两个内角的和可得∠BED=∠A+∠C，∠BDC=∠BED+∠B，再根据已知条件可得∠BDC=∠A+∠C+∠B即可求解。
10.①②；③；平行线的判定与性质
考点：平行线的判定与性质，推理与论证
解：如果∠B+∠D=180°，AB∥CD，那么BC∥DE．理由如下：∵AB∥CD（已知），
∴∠B=∠C（两直线平行，内错角相等），
又∵∠B+∠D=180°（已知），
∴∠C+∠D=180°，
∴BC∥DE（同旁内角互补，两直线平行）．
故答案为：①②，③，平行线的判定与性质．
分析：根据平行线的性质和已知条件易得∠C+∠D=180°，再根据同旁内角互补，两直线平行可得BC∥DE。
11.
考点：角的平分线，三角形的外角性质，探索图形规律
解：∵ 平分 , 平分 ，
?.
∵ ，
即 ，
∴ .
∵ ，
，
.
同理可得
∴ .
故答案为： .
分析：利用角平分线的性质，三角形外角的性质，易证 ，进而可求 ，由于 ，以此类推即可得出答案.
12.三角形的一个外角等于喝它不相邻的两个内角的和；角平分线的定义；等量代换
考点：三角形内角和定理，三角形的外角性质，推理与论证
解：根据证明步骤得，每一步的依据是三角形的一个外角等于喝它不相邻的两个内角的和；角平分线的定义；等量代换分析：由角平分线的性质可得∠2= ∠ACD，∠1=∠ABC，根据三角形的一个外角等于和它不相邻的两个内角的和可得：∠2=∠1+∠BEC，∠ACD=∠A+∠ABC，代入整理即可求得∠A=2∠BEC。
三、解答题
13. 解：∵∠1=∠B，∠2=∠3，
∴∠ADC=∠1+∠2=∠B+∠3，
∵∠4=∠B+∠3=80°，
∴∠ADC=80°.
考点：三角形的外角性质
分析：分别由∠1和∠B相等，∠2和∠3相等，把∠ADC转化为求∠B和∠3之和，现知∠4的度数，则利用三角形外角和定理可求∠B和∠3之和，则 ∠ADC的度数可知.
14. 证明：AD∥BC，
∠B=∠EAD,∠C=∠DAC,
AD平分外角∠EAC，
∠EAD=∠DAC
∠B=∠C
考点：同位角、内错角、同旁内角，三角形的外角性质
分析：根据同位角和内错角相等，利用角平分线的性质，可证明。
15. ；两直线平行，同位角相等；；等量代换；等式的性质；DAC；DAC；等量代换；内错角相等，两直线平行
分析：根据平行线的性质以及判定定理填写即可．
考点：同位角、内错角、同旁内角，平行线的判定与性质
解： （已知）
（两直线平行，同位角相等）
（已知）
（等量代换）
（已知）
（等式的性质）
即
（等量代换）
（内错角相等，两直线平行）
16. （1）证明：延长AC交BO于点P，

∵∠APB是△APO的外角，∴∠APB=∠CAO+∠AOB
∵∠ACB是△CPB的外角，
∴∠ACB=∠APB+∠CBO=∠CAO+∠AOB+∠CBO；
（2）根据(1)中的结论，∠A+∠B+∠C=∠BOC；∠D+∠E+∠F=∠EOD，
∵∠EOD=∠BOC=140°，
∴∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠EOD=280°．
考点：三角形内角和定理，三角形的外角性质
分析：（1） 延长AC交BO于点P?，根据三角形外角的性质，根据等量代换，即可得到答案；
（2）根据（1）中的结论，结合三角形的内角和定理即可得到答案。
17. （1）解：∵∠A=50°，∠C=30°，∴∠BDO=80°；∵∠BOD=70°，∴∠B=30°
（2）解：∠BOC=∠A+∠B+∠C.
理由：∵∠BOC=∠BEC +∠C，∠BEC=∠A+∠B，
∴∠BOC=∠A+∠B+∠C
考点：三角形的外角性质
分析：（1）由三角形的一个外角等于和它不相邻的两个内角的和可求得∠BDO的度数，然后用三角形内角和定理可求解；
（2）由三角形的一个外角等于和它不相邻的两个内角的和可得 ∠BOC=∠BEC +∠C，∠BEC=∠A+∠B， 代入整理即可求解.
18. （1）解：∵BD平分∠ABC，∠ABD＝25°
∴∠ABC=2∠ABD=50°，
∵AE⊥BC
∴∠AEB=∠AEC=90°
∴∠BAE=180°－∠AEB－∠ABC=40°
∵∠BAE：∠CAE＝4：6，
解得：∠CAE＝60°
（2）证明：在△CAE中，∠CAE＝60°，∠AEC=90°
∴∠C=180°－∠CAE－∠AEC=30°
∵∠CDF＝60°
∴∠DFB=∠CDF＋∠C=90°
∴DF⊥BC.
考点：垂线，三角形内角和定理，角平分线的性质
分析：（1）根据角平分线的定义可得∠ABC=2∠ABD=50°，然后根据垂直的定义可得∠AEB=∠AEC=90°，然后根据三角形的内角和定理即可求出∠BAE，然后根据已知比例式即可求出结论；（2）根据三角形的内角和定理即可求出∠C，然后根据三角形外角的性质即可求出∠DFB=90°，最后根据垂直的定义即可证出结论.
_21?????????è?????(www.21cnjy.com)_