第4章 图形与坐标单元提高测试卷(含解析)
文档属性
| 名称 | 第4章 图形与坐标单元提高测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-17 15:17:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版八年级数学上册第4章图形与坐标单元提高测试卷(含解析)
一、选择题(共10题;共30分)
1.下列数据不能确定目标的位置是(???
)
A.?教室内的3排2列????????????????B.?东经100°北纬45°????????????????C.?永林大道12号????????????????D.?南偏西40°
2.已知小明从点O出发,先向西走10米,再向南走20米,
到达点M,如果点M的位置用
表示,那么
表示的位置是(?
)
A.?A???????????????????????????????????????????B.?B???????????????????????????????????????????C.?C??????????????????????????????????????????D.?D
3.在某个电影院里,如果用(2,15)表示2排15号,那么5排9号可以表示为( )
A.?(2,15)????????????????????????B.?(2,5)?????????????????????????C.?(5,9)?????????????????????????D.?(9,5)
4.点P在第三象限,点P到
轴的距离是5,到
轴的距离是3,则点P的坐标(?
)
A.?(3,-5)???????????????????????B.?(-5,-3)??????????????????????????C.?(-3,-5)???????????????????????????D.?(-3,5)
5.在平面直角坐标系中,若点P(x,
x-4)在第四象限,则x的取值范围为(???
)
A.?x>0??????????????????????????????????B.?x<4??????????????????????????????????C.?0<x<4???????????????????????????????????D.?x>4
6.在如图所示的网格中有M,N,P,Q四个点,鹏鹏在该网格中建立了一个平面直角坐标系,然后得到点M的坐标为(﹣3,﹣1),点P的坐标为(0,﹣2),则点N和点Q的坐标分别为(??
)
A.?(2,1),(1,﹣2)??????????????????????????????????????B.?(1,1),(2,﹣2)
C.?(2,1),(﹣1,2)??????????????????????????????????D.?(1,1),(﹣2,2)
7.已知点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2),则点A的变换是(?
)
A.?先向左平移1个单位,再向上平移2个单位??????????B.?先向右平移1个单位,再向下平移2个单位
C.?先向左平移1个单位,再向下平移2个单位?????????
D.?先向右平移1个单位,再向上平移2个单位
8.已知点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则A(a,b)关于x轴对称的点的坐标为(??
)
A.?(1,﹣5)??????????????????????B.?(1,5)??????????????????????C.?(﹣1,5)??????????????????????D.?(﹣1,﹣5)
9.线段AB两端点坐标分别为A(
),B(
),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1
,
则A1、B1的坐标分别为(?
)
A.?A1(1,8),B1(-2,5)???????????????????????????????????????B.?A1(3,2),B1(0,-1)
C.?A1(-3,8),B1(-6,5)??????????????????????????????????????D.?A1(-5,2),B1(-8,-1)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),那么A2020坐标为( )
A.?(2020,1)?????????????????B.?(2020,0)???????????????????C.?(1010,1)???????????????????D.?(1010,0)
二、填空题(共6题;共18分)
11.若点P(2-m,m+1)在x轴上,则P点坐标为________.
12.在平面直角坐标系中,已知点P的坐标是(3,m),O为坐标原点,连接OP,若OP的长为5,则点P的坐标为________.
13.已知
的面积为16,其中两个顶点的坐标分别是
,顶点C在y轴上,那么点C的坐标为
________
14.同学们玩过五子棋吗?它的比赛规则是只要同色五子先成一条直线就算胜.如图是两人玩的一盘棋,若白①的位置是(2,-5),黑②的位置是(3,-4),现在轮到黑棋走,你认为黑棋放在________位置就可获胜.
15.点P(x,y)经过某种变换后到点
(-y+1,x+2),我们把点
(-y+1,x+2)叫做点P(x,y)的终结点,已知点
的终结点为
,点
的终结点为
,点
的终结点为
,这样依次得到
、
、
、
…
若点
的坐标为(2,0),则点
的坐标为________
16.如图,长方形BCDE的各边分别平行于x
轴或y
轴,物体甲和物体乙分别由点
同时出发,沿长方形BCDE
的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是________.
三、解答题(共7题;共52分)
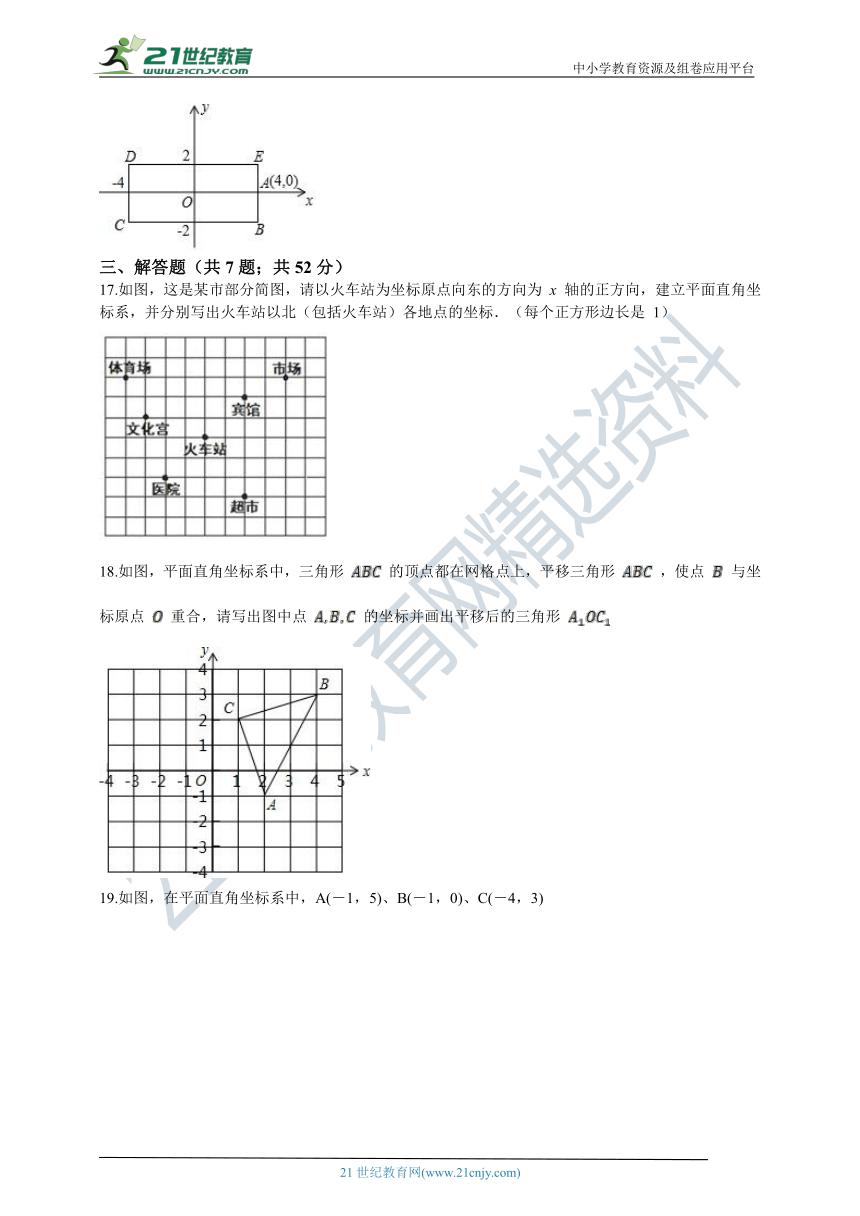
17.如图,这是某市部分简图,请以火车站为坐标原点向东的方向为
x
轴的正方向,建立平面直角坐标系,并分别写出火车站以北(包括火车站)各地点的坐标.(每个正方形边长是
1)
18.如图,平面直角坐标系中,三角形
的顶点都在网格点上,平移三角形
,使点
与坐标原点
重合,请写出图中点
的坐标并画出平移后的三角形
19.如图,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1)先把△ABC向左平移一个单位得到△A′B′C′,作出△A′B′C′关于y轴对称的△DEF(其中D、E、F分别是A′、B′、C′的对应点,不写画法)
(2)直接写出D、E、F三点的坐标
(3)在y轴的正半轴上存在一点P,使△PEF的面积等于△DEF的面积,则P的坐标为________
20.如下图,某日江苏省4艘渔船在回港途中,突遭9级强风,船上共35名船员遇险,岛上边防战士接到命令后立即出发,进行拉网式搜救。
以小岛为观测点,你能告诉边防战士渔船A、B、C、D位置吗?小岛南偏西60°方向的15km处是什么?
21.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),解答下列问题:
(1)画出△ABC关于y轴对称的△A1B
1C1
,
并写出点A1的坐标:
(2)在x轴上找一点P,使A1P+AP的和最小.
22.如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.
23.在平面直角坐标系中.
(1)已知点P(2a-6,a+4)在y轴上,求点P的坐标;
(2)已知两点A(-3,m-1),B(n+1,4)若AB∥x
轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)在(1)(2)的条件下,如果线段
AB
的长度是6,试判断以P、A、B为顶点的三角形的形状,并说明理由.
答案
一、选择题
1.A、教室内的3排2列,能确定目标的位置,故本选项不合题意;
?B、东经100°北纬45°,能确定目标的位置,故本选项不合题意;
?C、永林大道12号,能确定目标的位置,故本选项不合题意;
?D、南偏西40°,不能确定目标的位置,故本选项符合题意.
故答案为:D.
2.解:由题意可知:横坐标表示向东西走的路程,纵坐标表示向南北走的路程,向西走用负数表示,向南走用负数表示,且图中每个单位表示10米
∴
表示从点O出发,向东走10米,再向南走10米,
∴
表示的位置是向东10米,向南10米,结合图形即为点D
故答案为:D
3.解:∵(2,15)表示2排15号可知第一个数表示排,第二个数表示号
∴5排9号可以表示为(5,9),
故答案为:C.
4.解:∵点P在第三象限,点P到x轴的距离是5,到y轴的距离是3,
∴点P的横坐标为?3,纵坐标为?5,
∴点P的坐标为(?3,?5).
故答案为:C.
5.解:∵点P(x,
x-4)在第四象限
∴
解得0<x<4.
故答案为:C.
6.解:如图建立平面直角坐标系,
则点N和点Q的坐标分别为(1,1),(﹣2,2),
故答案为:D.
7.解:?∵点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2)
,
∴点A先向左平移1个单位,再向上平移两个单位.
故答案为:A.
8.解:∵P(﹣1﹣2a,5)关于x轴的对称点的坐标是(﹣1﹣2a,﹣5),
Q(3,b)关于y轴的对称点的坐标是(﹣3,b);
又∵
点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同
,
∴﹣1﹣2a=﹣3,b=﹣5;
∴a=1,
∴点A的坐标是(1,﹣5);
∴A点关于x轴对称的点的坐标为(1,5).
故答案为:B.
9.解:线段先向右平移4个单位长度,即让原横坐标都加4,纵坐标保持不变,向下平移2个单位长度,即让原横坐标保持不变,纵坐标都减2,所以A1的横坐标为:-1+4=3,纵坐标为:4-2=2;B1的横坐标为:-4+4=0,纵坐标为:1-2=-1,所以A1坐标为(3,2),B1坐标为(0,-1).
故答案为:B.
10.解:由图象可知:纵坐标每四个点循环一次,而2020=505×4,
故A2020的纵坐标与A4的纵坐标相同,都等于0;
由A4(2,0),A8(4,0),A12(6,0)…,
可得到规律A4n(2n,0)(n为不为0的自然数),
当n=505时,A2020(1010,0).
故答案为:D.
二、填空题
11.解:∵点P(2-m,m+1)在x轴上,
∴m+1=0,
解得:m=-1,
∴2-m=3,
∴P点坐标为(3,0),
故答案为:(3,0)
12.解:由题意可知:
解得:m=±4
∴P点坐标为:(3,4)或(3,-4)
故答案为:(3,4)或(3,-4).
13.解:
∵
∴AB=8
∵
的面积为16
∴
=16
∴OC=4
∴点C的坐标为(0,4)或(0,-4)
故答案为:(0,4)或(0,-4)
14.解:如图所示,黑棋放在图中三角形位置,就能获胜,
∵白①的位置是:(2,?5),黑②的位置是:(3,?4),
∴P点为坐标原点的位置,
∴黑棋放在(3,0)或(8,?5)位置就能获胜.
故答案为:(3,0)或(8,?5).
15.解:根据题意得点P1的坐标为(2,0),则点P2的坐标为(1,4),点P3的坐标为(-3,3),点P4的坐标为(-2,-1),点P5的坐标为(2,0),…,
而2020=4×505,
所以点P2020的坐标与点P4的坐标相同,为(-2,-1).
故答案为:(-2,-1).
16.矩形的边长为8和4,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为24×1,物体甲行的路程为24×
=8物体乙行的路程为24×
=16,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为24×2,物体甲行的路程为24×2×
=16,物体乙行的路程为24×2×
=32,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为24×3,物体甲行的路程为24×3×
=24,物体乙行的路程为24×3×
=48,在A点相遇;
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2020÷3=673…1,
故两个物体运动后的第2019次相遇地点的是点A,
即物体甲行的路程为24×1×
=8,物体乙行的路程为24×1×
=16时,达到第2020次相遇,
此时相遇点的坐标为:(-2,2),
故答案为:(-2,2).
三、解答题
17.
解:以火车站为坐标原点向东的方向为
x
轴的正方向,建立平面直角坐标系如下所示
由坐标系可知:火车站(0,0),文化宫(-3,1),体育场(-4,3),宾馆(2,2),市场(4,3).
18.
解:(1)A(2,-1),B(4,3),C(1,2)(2)三角形A1OC1为所求。
画图注意:在坐标系中画对一个点给一分
要在坐标系中标出A1
,
C1
,
不标的扣一分。
19.
(1)解:
(2)解:D(-2,-5)、E(-2,0)、F(-5,-3)
(3)(7,0)
20.解:图可知,渔船A在小岛北偏东50°方向距离小岛25km处,渔船B在小岛正南方向距离小岛20km处,渔船C在小岛北偏西30°方向距离小岛30km处,渔船D在小岛南偏东75°方向距离小岛35km处,小岛南偏西60°方向的15km处是航标灯
21
(1)解:如图所示:△A1B1C1
,
即为所求,
点A1的坐标为:(﹣2,4);
(2)解:如图所示:P点即为所求.
22.解:∵SABCO=SOEGF﹣S△ADO﹣S△OCF﹣S△BGC﹣SDEBA
,
∴SABCO=8×4﹣
﹣
﹣
﹣
=14.5.
23.
(1)解:根据题意知,2a﹣6=0,解得:a=3,
∴点
P
的坐标为(0,7)
(2)解:∵AB∥x
轴,
∴m﹣1=4,解得
m=5,∵点
B
在第一象限,
∴n+1>0,解得
n>﹣1
(3)解:由(2)知点
A(﹣3,4),
∵AB=6,且点
B
在第一象限,
∴点
B(3,4),
由点
P(0,7)可得
PA2=(﹣3﹣0)2+(4﹣7)2=18、PB2=(3﹣0)2+(4﹣7)2=18,
∵AB2=36,
∴PA2+PB2=AB2
,
且PA=PB,
因此,△PAB是等腰直角三角形。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版八年级数学上册第4章图形与坐标单元提高测试卷(含解析)
一、选择题(共10题;共30分)
1.下列数据不能确定目标的位置是(???
)
A.?教室内的3排2列????????????????B.?东经100°北纬45°????????????????C.?永林大道12号????????????????D.?南偏西40°
2.已知小明从点O出发,先向西走10米,再向南走20米,
到达点M,如果点M的位置用
表示,那么
表示的位置是(?
)
A.?A???????????????????????????????????????????B.?B???????????????????????????????????????????C.?C??????????????????????????????????????????D.?D
3.在某个电影院里,如果用(2,15)表示2排15号,那么5排9号可以表示为( )
A.?(2,15)????????????????????????B.?(2,5)?????????????????????????C.?(5,9)?????????????????????????D.?(9,5)
4.点P在第三象限,点P到
轴的距离是5,到
轴的距离是3,则点P的坐标(?
)
A.?(3,-5)???????????????????????B.?(-5,-3)??????????????????????????C.?(-3,-5)???????????????????????????D.?(-3,5)
5.在平面直角坐标系中,若点P(x,
x-4)在第四象限,则x的取值范围为(???
)
A.?x>0??????????????????????????????????B.?x<4??????????????????????????????????C.?0<x<4???????????????????????????????????D.?x>4
6.在如图所示的网格中有M,N,P,Q四个点,鹏鹏在该网格中建立了一个平面直角坐标系,然后得到点M的坐标为(﹣3,﹣1),点P的坐标为(0,﹣2),则点N和点Q的坐标分别为(??
)
A.?(2,1),(1,﹣2)??????????????????????????????????????B.?(1,1),(2,﹣2)
C.?(2,1),(﹣1,2)??????????????????????????????????D.?(1,1),(﹣2,2)
7.已知点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2),则点A的变换是(?
)
A.?先向左平移1个单位,再向上平移2个单位??????????B.?先向右平移1个单位,再向下平移2个单位
C.?先向左平移1个单位,再向下平移2个单位?????????
D.?先向右平移1个单位,再向上平移2个单位
8.已知点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则A(a,b)关于x轴对称的点的坐标为(??
)
A.?(1,﹣5)??????????????????????B.?(1,5)??????????????????????C.?(﹣1,5)??????????????????????D.?(﹣1,﹣5)
9.线段AB两端点坐标分别为A(
),B(
),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1
,
则A1、B1的坐标分别为(?
)
A.?A1(1,8),B1(-2,5)???????????????????????????????????????B.?A1(3,2),B1(0,-1)
C.?A1(-3,8),B1(-6,5)??????????????????????????????????????D.?A1(-5,2),B1(-8,-1)
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),那么A2020坐标为( )
A.?(2020,1)?????????????????B.?(2020,0)???????????????????C.?(1010,1)???????????????????D.?(1010,0)
二、填空题(共6题;共18分)
11.若点P(2-m,m+1)在x轴上,则P点坐标为________.
12.在平面直角坐标系中,已知点P的坐标是(3,m),O为坐标原点,连接OP,若OP的长为5,则点P的坐标为________.
13.已知
的面积为16,其中两个顶点的坐标分别是
,顶点C在y轴上,那么点C的坐标为
________
14.同学们玩过五子棋吗?它的比赛规则是只要同色五子先成一条直线就算胜.如图是两人玩的一盘棋,若白①的位置是(2,-5),黑②的位置是(3,-4),现在轮到黑棋走,你认为黑棋放在________位置就可获胜.
15.点P(x,y)经过某种变换后到点
(-y+1,x+2),我们把点
(-y+1,x+2)叫做点P(x,y)的终结点,已知点
的终结点为
,点
的终结点为
,点
的终结点为
,这样依次得到
、
、
、
…
若点
的坐标为(2,0),则点
的坐标为________
16.如图,长方形BCDE的各边分别平行于x
轴或y
轴,物体甲和物体乙分别由点
同时出发,沿长方形BCDE
的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是________.
三、解答题(共7题;共52分)
17.如图,这是某市部分简图,请以火车站为坐标原点向东的方向为
x
轴的正方向,建立平面直角坐标系,并分别写出火车站以北(包括火车站)各地点的坐标.(每个正方形边长是
1)
18.如图,平面直角坐标系中,三角形
的顶点都在网格点上,平移三角形
,使点
与坐标原点
重合,请写出图中点
的坐标并画出平移后的三角形
19.如图,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1)先把△ABC向左平移一个单位得到△A′B′C′,作出△A′B′C′关于y轴对称的△DEF(其中D、E、F分别是A′、B′、C′的对应点,不写画法)
(2)直接写出D、E、F三点的坐标
(3)在y轴的正半轴上存在一点P,使△PEF的面积等于△DEF的面积,则P的坐标为________
20.如下图,某日江苏省4艘渔船在回港途中,突遭9级强风,船上共35名船员遇险,岛上边防战士接到命令后立即出发,进行拉网式搜救。
以小岛为观测点,你能告诉边防战士渔船A、B、C、D位置吗?小岛南偏西60°方向的15km处是什么?
21.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),解答下列问题:
(1)画出△ABC关于y轴对称的△A1B
1C1
,
并写出点A1的坐标:
(2)在x轴上找一点P,使A1P+AP的和最小.
22.如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.
23.在平面直角坐标系中.
(1)已知点P(2a-6,a+4)在y轴上,求点P的坐标;
(2)已知两点A(-3,m-1),B(n+1,4)若AB∥x
轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)在(1)(2)的条件下,如果线段
AB
的长度是6,试判断以P、A、B为顶点的三角形的形状,并说明理由.
答案
一、选择题
1.A、教室内的3排2列,能确定目标的位置,故本选项不合题意;
?B、东经100°北纬45°,能确定目标的位置,故本选项不合题意;
?C、永林大道12号,能确定目标的位置,故本选项不合题意;
?D、南偏西40°,不能确定目标的位置,故本选项符合题意.
故答案为:D.
2.解:由题意可知:横坐标表示向东西走的路程,纵坐标表示向南北走的路程,向西走用负数表示,向南走用负数表示,且图中每个单位表示10米
∴
表示从点O出发,向东走10米,再向南走10米,
∴
表示的位置是向东10米,向南10米,结合图形即为点D
故答案为:D
3.解:∵(2,15)表示2排15号可知第一个数表示排,第二个数表示号
∴5排9号可以表示为(5,9),
故答案为:C.
4.解:∵点P在第三象限,点P到x轴的距离是5,到y轴的距离是3,
∴点P的横坐标为?3,纵坐标为?5,
∴点P的坐标为(?3,?5).
故答案为:C.
5.解:∵点P(x,
x-4)在第四象限
∴
解得0<x<4.
故答案为:C.
6.解:如图建立平面直角坐标系,
则点N和点Q的坐标分别为(1,1),(﹣2,2),
故答案为:D.
7.解:?∵点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2)
,
∴点A先向左平移1个单位,再向上平移两个单位.
故答案为:A.
8.解:∵P(﹣1﹣2a,5)关于x轴的对称点的坐标是(﹣1﹣2a,﹣5),
Q(3,b)关于y轴的对称点的坐标是(﹣3,b);
又∵
点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同
,
∴﹣1﹣2a=﹣3,b=﹣5;
∴a=1,
∴点A的坐标是(1,﹣5);
∴A点关于x轴对称的点的坐标为(1,5).
故答案为:B.
9.解:线段先向右平移4个单位长度,即让原横坐标都加4,纵坐标保持不变,向下平移2个单位长度,即让原横坐标保持不变,纵坐标都减2,所以A1的横坐标为:-1+4=3,纵坐标为:4-2=2;B1的横坐标为:-4+4=0,纵坐标为:1-2=-1,所以A1坐标为(3,2),B1坐标为(0,-1).
故答案为:B.
10.解:由图象可知:纵坐标每四个点循环一次,而2020=505×4,
故A2020的纵坐标与A4的纵坐标相同,都等于0;
由A4(2,0),A8(4,0),A12(6,0)…,
可得到规律A4n(2n,0)(n为不为0的自然数),
当n=505时,A2020(1010,0).
故答案为:D.
二、填空题
11.解:∵点P(2-m,m+1)在x轴上,
∴m+1=0,
解得:m=-1,
∴2-m=3,
∴P点坐标为(3,0),
故答案为:(3,0)
12.解:由题意可知:
解得:m=±4
∴P点坐标为:(3,4)或(3,-4)
故答案为:(3,4)或(3,-4).
13.解:
∵
∴AB=8
∵
的面积为16
∴
=16
∴OC=4
∴点C的坐标为(0,4)或(0,-4)
故答案为:(0,4)或(0,-4)
14.解:如图所示,黑棋放在图中三角形位置,就能获胜,
∵白①的位置是:(2,?5),黑②的位置是:(3,?4),
∴P点为坐标原点的位置,
∴黑棋放在(3,0)或(8,?5)位置就能获胜.
故答案为:(3,0)或(8,?5).
15.解:根据题意得点P1的坐标为(2,0),则点P2的坐标为(1,4),点P3的坐标为(-3,3),点P4的坐标为(-2,-1),点P5的坐标为(2,0),…,
而2020=4×505,
所以点P2020的坐标与点P4的坐标相同,为(-2,-1).
故答案为:(-2,-1).
16.矩形的边长为8和4,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为24×1,物体甲行的路程为24×
=8物体乙行的路程为24×
=16,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为24×2,物体甲行的路程为24×2×
=16,物体乙行的路程为24×2×
=32,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为24×3,物体甲行的路程为24×3×
=24,物体乙行的路程为24×3×
=48,在A点相遇;
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2020÷3=673…1,
故两个物体运动后的第2019次相遇地点的是点A,
即物体甲行的路程为24×1×
=8,物体乙行的路程为24×1×
=16时,达到第2020次相遇,
此时相遇点的坐标为:(-2,2),
故答案为:(-2,2).
三、解答题
17.
解:以火车站为坐标原点向东的方向为
x
轴的正方向,建立平面直角坐标系如下所示
由坐标系可知:火车站(0,0),文化宫(-3,1),体育场(-4,3),宾馆(2,2),市场(4,3).
18.
解:(1)A(2,-1),B(4,3),C(1,2)(2)三角形A1OC1为所求。
画图注意:在坐标系中画对一个点给一分
要在坐标系中标出A1
,
C1
,
不标的扣一分。
19.
(1)解:
(2)解:D(-2,-5)、E(-2,0)、F(-5,-3)
(3)(7,0)
20.解:图可知,渔船A在小岛北偏东50°方向距离小岛25km处,渔船B在小岛正南方向距离小岛20km处,渔船C在小岛北偏西30°方向距离小岛30km处,渔船D在小岛南偏东75°方向距离小岛35km处,小岛南偏西60°方向的15km处是航标灯
21
(1)解:如图所示:△A1B1C1
,
即为所求,
点A1的坐标为:(﹣2,4);
(2)解:如图所示:P点即为所求.
22.解:∵SABCO=SOEGF﹣S△ADO﹣S△OCF﹣S△BGC﹣SDEBA
,
∴SABCO=8×4﹣
﹣
﹣
﹣
=14.5.
23.
(1)解:根据题意知,2a﹣6=0,解得:a=3,
∴点
P
的坐标为(0,7)
(2)解:∵AB∥x
轴,
∴m﹣1=4,解得
m=5,∵点
B
在第一象限,
∴n+1>0,解得
n>﹣1
(3)解:由(2)知点
A(﹣3,4),
∵AB=6,且点
B
在第一象限,
∴点
B(3,4),
由点
P(0,7)可得
PA2=(﹣3﹣0)2+(4﹣7)2=18、PB2=(3﹣0)2+(4﹣7)2=18,
∵AB2=36,
∴PA2+PB2=AB2
,
且PA=PB,
因此,△PAB是等腰直角三角形。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
