第3章 圆的基本性质单元提高测试卷(含解析)
文档属性
| 名称 | 第3章 圆的基本性质单元提高测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-17 19:48:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版九年级数学上册第3章圆的基本性质单元提高测试卷解析版
一、选择题(共10题;共30分)
1.如图是几种常见的汽车轮毂图案,图案围绕中心旋转90°后能与原来的图案重合的是(???
)
A.???????????????????????B.??????????????????????????C.????????????????????????D.?
2.矩形
中,
,
,如果分别以
、
为圆心的两圆外切,且点
在圆
内,点
在圆
外,那么圆
的半径
的取值范围是(????
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
3.如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB的度数是(???
)
A.?70°???????????????????????????????????B.?80°???????????????????????????????????C.?82°???????????????????????????????????????D.?85°
4.如图,已知AB是⊙O的直径,点C,D在⊙O上,弧AC的度数为100°,则∠D的大小为(??
)
A.?30°?????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
5.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB的长为(??
)
A.?8???????????????????????????????????????B.?12??????????????????????????????????????C.?16?????????????????????????????????????D.?2
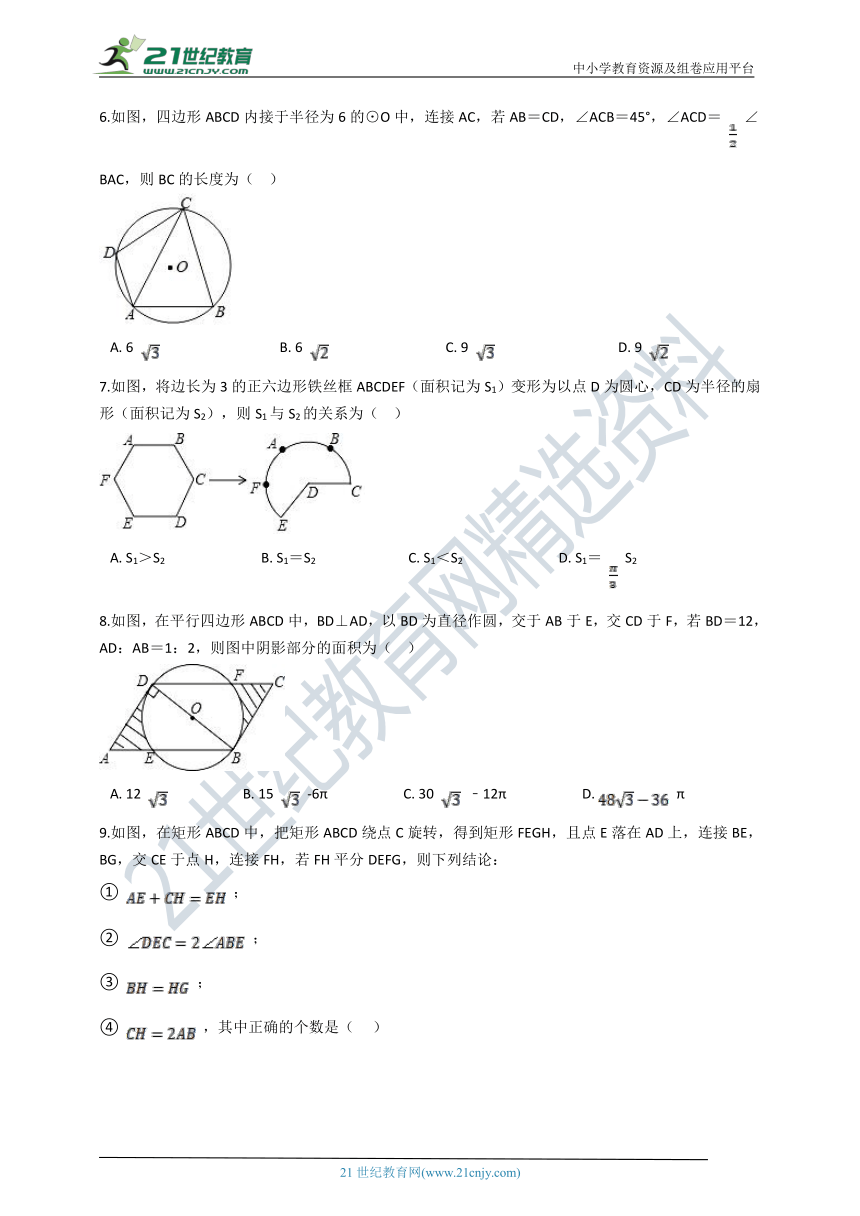
6.如图,四边形ABCD内接于半径为6的⊙O中,连接AC,若AB=CD,∠ACB=45°,∠ACD=
∠BAC,则BC的长度为(??
)
A.?6
???????????????????????????????????B.?6
??????????????????????????????????C.?9
????????????????????????????????????D.?9
7.如图,将边长为3的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为(??
)
A.?S1>S2????????????????????????????B.?S1=S2???????????????????????????C.?S1<S2????????????????????????????D.?S1=
S2
8.如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为(??
)
A.?12
??????????????????????B.?15
-6π??????????????????????C.?30
﹣12π??????????????????????D.?
π
9.如图,在矩形ABCD中,把矩形ABCD绕点C旋转,得到矩形FEGH,且点E落在AD上,连接BE,BG,交CE于点H,连接FH,若FH平分DEFG,则下列结论:
①
;
②
;
③
;
④
,其中正确的个数是(???
)
A.?1个?????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10.如图,正方形ABCD和等边△AEF都内接于圆O,EF与BC,CD别相交于点G,H.若AE=6,则EG的长为(??
)
A.????????????????????????????????B.?3﹣
??????????????????????????????????C.?????????????????????????????????D.?2
﹣3
二、填空题(共6题;共18分)
11.若扇形的圆心角为45°,半径为3,则该扇形的弧长为________。
12.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是________.
13.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为________.
14.如图,
中,
以
为直径的
交
于点
为
的中点,则图中阴影部分的面积为________.
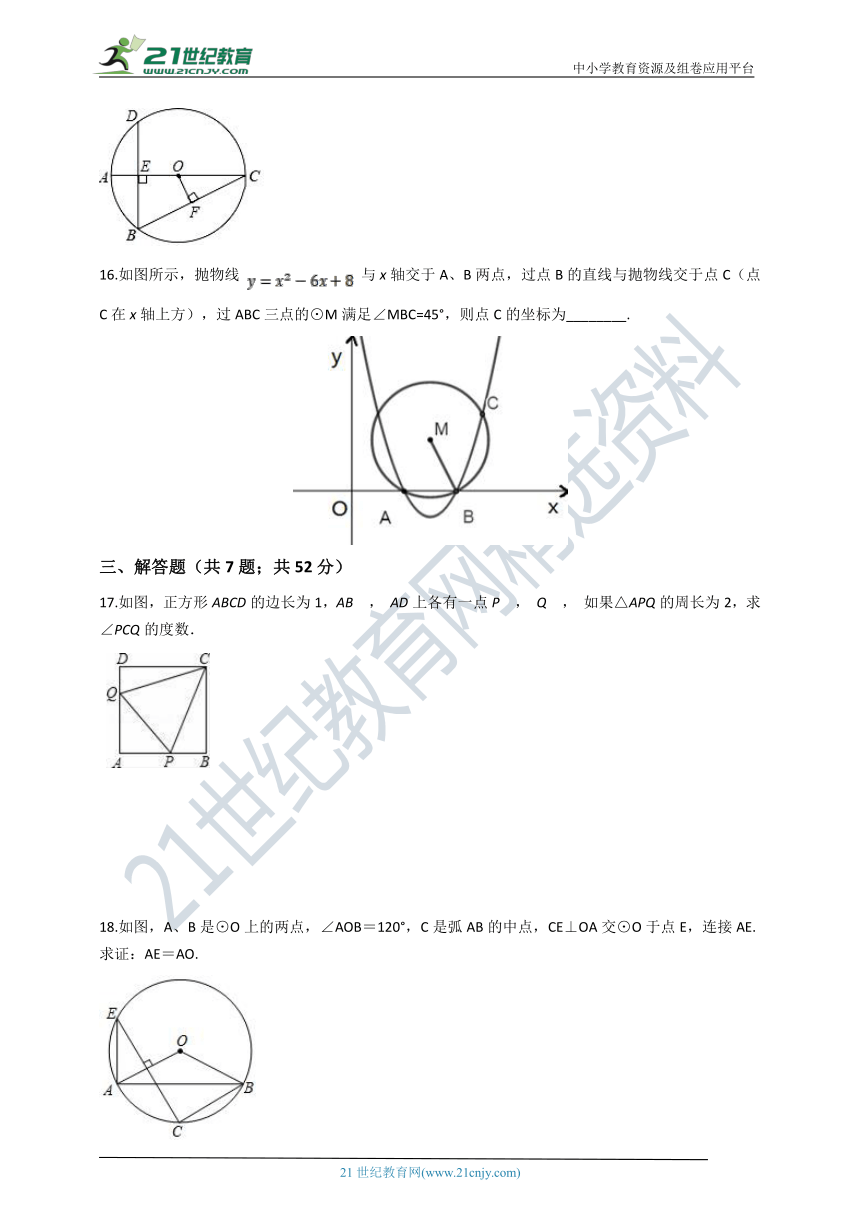
15.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是________cm.
16.如图所示,抛物线
与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为________.
?????????
三、解答题(共7题;共52分)
17.如图,正方形ABCD的边长为1,AB
,
AD上各有一点P
,
Q
,
如果△APQ的周长为2,求∠PCQ的度数.
18.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
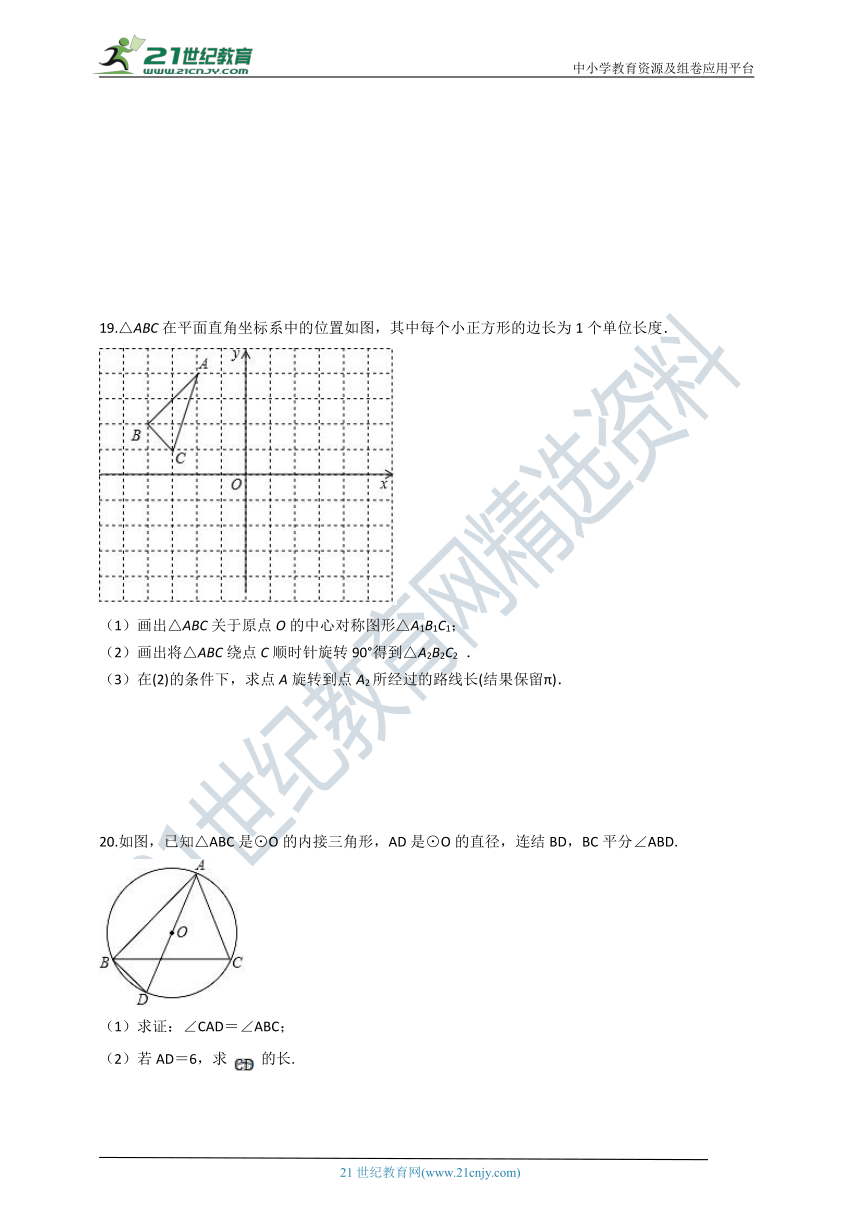
19.△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出将△ABC绕点C顺时针旋转90°得到△A2B2C2
.
(3)在(2)的条件下,求点A旋转到点A2所经过的路线长(结果保留π).
20.如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
(1)求证:∠CAD=∠ABC;
(2)若AD=6,求
的长.
21.如图,AB是⊙O的直径,弦CD⊥AB于点E
,G是弧AC上的点,AG,DC延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的长.
22.如图,正六边形ABCDEF的对称中心P在反比例函数y=
(k>0,x>0)的图象上边CD在x轴上,点B在y轴上,已知CD=4.
(1)点A是否在该反比例函数的图象上?请说明理由.
(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标;
(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
23.已知在平面直角坐标系中,抛物线y=x2+3x﹣a2+a+2(a>1)的图象交x轴于点A和点B(点A在点B左侧),与y轴交于点C,顶点为E.
(1)如图1,求线段AB的长度(用含a的式子表示)及抛物线的对称轴;
(2)如图2,当抛物线的图象经过原点时,在平面内是否存在一点P,使得以A、B、E、P为顶点的四边形能否成为平行四边形?如果能,求出P点坐标;如果不能,请说明理由;
(3)如图3,当a=3时,若M点为x轴上一动点,连结MC,将线段MC绕点M逆时针旋转90°得到线段MN,连结AC、CN、AN,则△ACN周长的最小值为多少?
答案
一、选择题
1.解:A、此图形旋转60°或60°的整数倍能与原来的图案重合;
B、此图形旋转45°或45°的整数倍能与原来的图案重合;
C、此图形旋转72°或72°的整数倍能与原来的图案重合;
D、此图形旋转36°或36°的整数倍能与原来的图案重合;
故答案为:B.
2.解:∵在矩形ABCD中,AB=5,BC=12,∴AC=
=13,
∵点D在⊙C内,点B在⊙C外,∴⊙C的半径R的取值范围为:5<R<12,
∴当⊙A和⊙C外切时,圆心距为13等于两圆半径之和,则R+r=13,
又∵5<R<12,则5<13-r<12,∴1<r<8.
故答案为:C.
3.解:延长AD交圆O于点E,连接CE
∴∠E=∠B=70°,∠ACE=90°
∴∠CAE=90°-70°=20°
∵∠B=70°,∠ACB=50°
∴∠BAC=180°-∠B-∠ACB=180°-70°-50°=60°
∴∠BAD=∠BAC-∠CAE=60°-20°=40°
∴∠ADB=180°-70°-40°=70°
故答案为:A.
4.解:连结AC,如图,
∵弧AC的度数为100°,
∴∠ABC=50°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°-∠ABC=90°-50°=40°,
∴∠D=∠BAC=40°.
故答案为:B.
5.解:连接OA,
∵⊙O的直径CD=20,OM:OD=3:5,
∴OD=10,OM=6,
∵AB⊥CD,
∴AM=
=
=8,
∴AB=2AM=16.
故答案为:C.
6.解:连接OA、OB,作BH⊥AC于H,如图,
∵AB=CD,
∴
=
,
∴∠CAD=∠ACB=45°,
∵∠BAD+∠BCD=180°,
∴∠ACD+∠ACB+∠CAD+∠BAC=180°,
∵∠ACD=
∠BAC
∴
∠BAC+45°+45°+∠BAC=180°,解得∠BAC=60°,
∵∠AOB=2∠ACB=90°,
∴△OAB为等腰直角三角形,
∴AB=
OA=6
,
在Rt△ABH中,∠BAH=60°,
∴AH=
AB=3
,BH=
AH=3
,
在Rt△BCH中,∵∠BCH=45°,
∴BC=
BH=
×3
=6
.
故答案为:A.
7.解:由题意:
=12,
∴S2=
×12×3=18,
∵S1=6×
×32=
,
∴S1>S2
,
故答案为:A.
8.解:连接OE,OF.
∵BD=12,AD:AB=1:2,
∴AD=4
,AB=8
,∠ABD=30°,
∴S△ABD=
=24
,S扇形DOE=
=6π,S△OEB=
=9
,
∵两个阴影的面积相等,
∴阴影面积=2×(24
﹣6π﹣9
)=30
﹣12π.
故答案为:C.
9.解:如图,作BM⊥EC于M.
?
∵CB=CE,
∴∠CBE=∠CEB,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠AEB=∠MEB,
∵∠A=∠BME=90°,BE=BE,
∴△BEA≌△BEM(AAS),
∴AE=EM,AB=BM.
∵∠BMH=∠GCH=90°,∠BHM=∠GHC,BM=AB=CG,
∴△BMH≌△GCH(AAS),
∴MH=CH,BH=HG,
∴EH=EM+MH=AE+CH,故①③符合题意,
∵∠AEB+∠ABE=90°,
∴2∠AEB+2∠ABE=180°,
∵∠DEC+∠AEC=180°,∠AEC=2∠AEB,
∴∠DEC+2∠AEB=180°,
∴∠DEC=2∠ABE,故②符合题意,
∵FH平分∠EFG,
∴∠EFH=45°,
∵∠FEH=90°,
∴AB=EF=EH,
∵EH>HM=CH,
∴CH<AB,故④不符合题意.
故答案为:C.
10.连接AC、BD、OF,AC与EF交于P点,则它们的交点为O点,如图,
∵正方形ABCD和等边△AEF都内接于圆O,
∴正方形ABCD和等边△AEF都是轴对称图形,直径AC是对称轴,
∴∠COF=60°,AC⊥BD,AC⊥EF,∠BCA=45°,
∴PE=PF=
EF=3,
在Rt△OPF中,OP=
OF=
OC,
∵OP=
PF=
,
∴PC=OP=
,
∵△PCG为等腰直角三角形,
∴PG=PC=
,
∴EG=PE﹣PG=3﹣
.
故答案为:B.
二、填空题
11.解:根据弧长公式:
,
故答案为:
.
12.解:过点
作
于
,连接
,如图,
则
,
在
中,
,
所以
与
之间的距离是3.
故答案为3.
13.解:∵AC=AD,∠A=30°,
∴∠ACD=∠ADC=75°,
∵AO=OC,
∴∠OCA=∠A=30°,
∴∠OCD=45°,即△OCE是等腰直角三角形,
在等腰Rt△OCE中,OC=2;
因此OE=
.
故答案为:
.
14.解:连接AD,
∵AB是直径,
∴∠ADB=90°,即AD⊥BC,
∵D为BC的中线,
∴△ABC是等腰三角形,
∴∠B=∠C=24°,
∴∠AOD=2∠B=48°,
∵AB=4,
∴半径为2,
∴S阴影=
,
故答案为:
.
15.解:连接OB,
∵AC是⊙O的直径,弦BD⊥AC,
∴BE=
BD=6cm,
在Rt△OEB中,OB2=OE2+BE2
,
即OB2=(OB﹣4)2+62
,
解得,OB=
,
则EC=AC﹣AE=9,
BC=
=
=3
,
∵OF⊥BC,
∴CF=
BC=
,
∴OF=
=
=
(cm).
故答案为:
.
16.解:y=x2-6x+8=(x-2)(x-4),故A(2,0),B(4,0),
根据垂径定理可知点M在AB的中垂线上,设M(3,a).
连接MC,过点M作ME∥x轴,过点B作BF垂直ME于点F,过点C作CE⊥ME于点E,
∵MB=MC,∠MBC=45°,
∴∠NCB=45°,
∴∠BMC=90°,
∵∠MEC=∠BFM=90°,
∴∠BMF=∠MCE,
∴△BMF≌△MCE,
∴ME=BF,MF=CE,
∵B(4,0),M(3,a).
∴CE=MF=1,EF=a-1,
∴C(4+a-1,a+1)即C(3+a,a+1),
由于点C在抛物线上,则有
a+1=(3+a)2-6(3+a)+8
解得a1=2,a2=-1,
根据圆心M在第一象限可得a2=-1不符合题意,故a=2,
∴C(5,3).
三、解答题
17.
解:如图所示,
△APQ的周长为2,即AP+AQ+PQ=2①,
正方形ABCD的边长是1,即AQ+QD=1,AP+PB=1,
∴AP+AQ+QD+PB=2②,
①﹣②得,PQ﹣QD﹣PB=0,
∴PQ=PB+QD
.
延长AB至M
,
使BM=DQ
.
连接CM
,
△CBM≌△CDQ(SAS),
∴∠BCM=∠DCQ
,
CM=CQ
,
∵∠DCQ+∠QCB=90°,
∴∠BCM+∠QCB=90°,即∠QCM=90°,
PM=PB+BM=PB+DQ=PQ
.
在△CPQ与△CPM中,
CP=CP
,
PQ=PM
,
CQ=CM
,
∴△CPQ≌△CPM(SSS),
∴∠PCQ=∠PCM=
∠QCM=45°.
18.
证明:连OC,OA,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴
,
∴AE=AC,
∴AE=AO
19.
(1)解:如图所示,△A1B1C1即为所求;
(2)解:如图所示,△A2B2C2即为所求;
(3)解:由勾股定理可得AC=
,
∴弧AA2的长=
.
20.
(1)证明∵BC平分∠ABD,
∴∠DBC=∠ABC
∴∠CAD=∠DBC
∴∠CAD=∠ABC
(2)解∵∠CAD=∠ABC,
∴
∵AD是⊙O的直径,AD=6,
∴
21.
(1)证明:∵
弦CD⊥AB
,∴
,
∴∠ADC=∠ACD,
∵
∠AGD=∠ACD,∴∠AGD=∠ADC,
∵四边形ABCG是圆内接四边形,
∴
∠FGC=∠ADC,∴
∠FGC=∠AGD;
(2)解:连接OD,∵CD⊥AB,CD=8,∴DE=CE=4,
在Rt△DOE中,DO2=OE2+ED2
,
∴DO2=(OD-2)2+42
,
解得OD=5,∴AE=10-2=8,
∴AD=.
22.
(1)解:过点P作x轴垂线PG,连接BP,CP,
∵P是正六边形ABCDEF的对称中心,CD=4,
∴BP=CP=4,G是CD的中点,
∴PG=2
,
∴P(4,2
),
∵P在反比例函数y=
上,
∴k=8
,
∴y=
,
连接AC交PB于G,则AC⊥PB,
由正六边形的性质得A(2,4
),
∴点A在反比例函数图象上
(2)解:过Q作QM⊥x轴于M,
∵六边形ABCDEF为正六边形,
∴∠EDM=60°,
设DM=b,则QM=
b,
∴Q(b+6,
b),
∵该反比例函数图象与DE交于点Q,
∴
b(b+6)=8
,
解得:b=﹣3+
,b=﹣3﹣
(不合题意舍去),
∴点Q的横坐标为3+
(3)解:连接AP,A(2,4
),B(0,2
),C(2,0),D(6,0),E(8,
),F(6,4
),
设正六边形向左平移m个单位,向上平移n个单位,则平移后点的坐标分别为
∴A(2﹣m,4
+n),B(﹣m,2
+n),C(2﹣m,n),D(6﹣m,n),E(8﹣m,2
+n),F(6﹣m,4
+n),
①将正六边形向左平移4个单位后,E(4,2
),F(2,4
);
则点E与F都在反比例函数图象上;
②将正六边形向右平移2个单位,再向上平移2
个单位后,C(4,2
),B(2,4
)
则点B与C都在反比例函数图象上
?
23.
(1)解:当y=0时,x2+3x﹣a2+a+2=0,
∴[x﹣(a﹣2)][x+(a+1)]=0,
∴x=a﹣2,或x=﹣a﹣1,
∵点A在点B左侧,
∴A(﹣a﹣1,0),B(a﹣2,0),
∴AB=a﹣2﹣(﹣a﹣1)=2a﹣1,
抛物线的对称轴为x=
=﹣
,即抛物线的对称轴为x=﹣
(2)解:存在,理由如下:
∵抛物线y=x2+3x﹣a2+a+2(a>1)的图象经过原点,a>1,
∴﹣a2+a+2=0,
解得:a=2,或a=﹣1(舍去),
∴a=2,
∴A(﹣3,0),B(0,0),y=x2+3x=(x+
)2﹣
,
∴E(﹣
,﹣
),
分情况讨论,如图2所示:
①若AB为平行四边形的边,则P点坐标为(
,﹣
)或(﹣
,﹣
);
②若AB为平行四边形的对角线,则P点坐标为(﹣
,﹣
);
综上所述,在平面内存在一点P,使得以A、B、E、P为顶点的四边形成为平行四边形,P点坐标为(
,﹣
)或(﹣
,﹣
)或(﹣
,﹣
)
(3)解:当a=3时,y=x2+3x﹣4,
此时A(﹣4,0),B(1,0),C(0,﹣4),
∴OA=4,OC=4,
设M(t,0),
∵将线段MC绕点M逆时针旋转90°得到线段MN,
∴OM=﹣t,
过点M作EF⊥x轴,过点N作NE⊥EF于点E,过点C作CF⊥EF于点F,如图3所示:
则∠MEN=∠CFM=90°,
由旋转的性质得:MN=MC,∠CMN=90°,
∴∠EMN+∠CMF=∠CMF+∠FCM=90°,
∴∠EMN=∠FCM,
在△MNE和△CMF中
,
∴△MNE≌△CMF(AAS),
∴MF=CF=OM=﹣t,EN=MF=OC=4,
∴点N的横坐标为Nx=4+t,点N的纵坐标为Ny=﹣t,
∴y=﹣x+4,
∴点N在直线l:y=﹣x+4上运动,
设直线l交x轴于点G,则G(4,0),
若使△ACN的周长最小,即使AN+CN最小,
∴作点A关于l的对称点A',连接A'C,A'N,
则AN=A'N,
当A'、N、C三点共线时,AN+CN最小=A'C,
由题意得:∠A'AO=45°,∠CAO=45°,
∴∠CAA'=90°,
∵G(4,0),
∴AG=OA+OG=8,AA'=
,
∵AC=
=
,
∴A'C=
=
,
∴A'C+AC=
+
,
∵△ACN的周长=AN+CN+AC,
∴△ACN周长的最小值为A'C+AC=4
+4
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版九年级数学上册第3章圆的基本性质单元提高测试卷解析版
一、选择题(共10题;共30分)
1.如图是几种常见的汽车轮毂图案,图案围绕中心旋转90°后能与原来的图案重合的是(???
)
A.???????????????????????B.??????????????????????????C.????????????????????????D.?
2.矩形
中,
,
,如果分别以
、
为圆心的两圆外切,且点
在圆
内,点
在圆
外,那么圆
的半径
的取值范围是(????
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
3.如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB的度数是(???
)
A.?70°???????????????????????????????????B.?80°???????????????????????????????????C.?82°???????????????????????????????????????D.?85°
4.如图,已知AB是⊙O的直径,点C,D在⊙O上,弧AC的度数为100°,则∠D的大小为(??
)
A.?30°?????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
5.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB的长为(??
)
A.?8???????????????????????????????????????B.?12??????????????????????????????????????C.?16?????????????????????????????????????D.?2
6.如图,四边形ABCD内接于半径为6的⊙O中,连接AC,若AB=CD,∠ACB=45°,∠ACD=
∠BAC,则BC的长度为(??
)
A.?6
???????????????????????????????????B.?6
??????????????????????????????????C.?9
????????????????????????????????????D.?9
7.如图,将边长为3的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为(??
)
A.?S1>S2????????????????????????????B.?S1=S2???????????????????????????C.?S1<S2????????????????????????????D.?S1=
S2
8.如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为(??
)
A.?12
??????????????????????B.?15
-6π??????????????????????C.?30
﹣12π??????????????????????D.?
π
9.如图,在矩形ABCD中,把矩形ABCD绕点C旋转,得到矩形FEGH,且点E落在AD上,连接BE,BG,交CE于点H,连接FH,若FH平分DEFG,则下列结论:
①
;
②
;
③
;
④
,其中正确的个数是(???
)
A.?1个?????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10.如图,正方形ABCD和等边△AEF都内接于圆O,EF与BC,CD别相交于点G,H.若AE=6,则EG的长为(??
)
A.????????????????????????????????B.?3﹣
??????????????????????????????????C.?????????????????????????????????D.?2
﹣3
二、填空题(共6题;共18分)
11.若扇形的圆心角为45°,半径为3,则该扇形的弧长为________。
12.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是________.
13.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为________.
14.如图,
中,
以
为直径的
交
于点
为
的中点,则图中阴影部分的面积为________.
15.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是________cm.
16.如图所示,抛物线
与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为________.
?????????
三、解答题(共7题;共52分)
17.如图,正方形ABCD的边长为1,AB
,
AD上各有一点P
,
Q
,
如果△APQ的周长为2,求∠PCQ的度数.
18.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
19.△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出将△ABC绕点C顺时针旋转90°得到△A2B2C2
.
(3)在(2)的条件下,求点A旋转到点A2所经过的路线长(结果保留π).
20.如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
(1)求证:∠CAD=∠ABC;
(2)若AD=6,求
的长.
21.如图,AB是⊙O的直径,弦CD⊥AB于点E
,G是弧AC上的点,AG,DC延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的长.
22.如图,正六边形ABCDEF的对称中心P在反比例函数y=
(k>0,x>0)的图象上边CD在x轴上,点B在y轴上,已知CD=4.
(1)点A是否在该反比例函数的图象上?请说明理由.
(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标;
(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
23.已知在平面直角坐标系中,抛物线y=x2+3x﹣a2+a+2(a>1)的图象交x轴于点A和点B(点A在点B左侧),与y轴交于点C,顶点为E.
(1)如图1,求线段AB的长度(用含a的式子表示)及抛物线的对称轴;
(2)如图2,当抛物线的图象经过原点时,在平面内是否存在一点P,使得以A、B、E、P为顶点的四边形能否成为平行四边形?如果能,求出P点坐标;如果不能,请说明理由;
(3)如图3,当a=3时,若M点为x轴上一动点,连结MC,将线段MC绕点M逆时针旋转90°得到线段MN,连结AC、CN、AN,则△ACN周长的最小值为多少?
答案
一、选择题
1.解:A、此图形旋转60°或60°的整数倍能与原来的图案重合;
B、此图形旋转45°或45°的整数倍能与原来的图案重合;
C、此图形旋转72°或72°的整数倍能与原来的图案重合;
D、此图形旋转36°或36°的整数倍能与原来的图案重合;
故答案为:B.
2.解:∵在矩形ABCD中,AB=5,BC=12,∴AC=
=13,
∵点D在⊙C内,点B在⊙C外,∴⊙C的半径R的取值范围为:5<R<12,
∴当⊙A和⊙C外切时,圆心距为13等于两圆半径之和,则R+r=13,
又∵5<R<12,则5<13-r<12,∴1<r<8.
故答案为:C.
3.解:延长AD交圆O于点E,连接CE
∴∠E=∠B=70°,∠ACE=90°
∴∠CAE=90°-70°=20°
∵∠B=70°,∠ACB=50°
∴∠BAC=180°-∠B-∠ACB=180°-70°-50°=60°
∴∠BAD=∠BAC-∠CAE=60°-20°=40°
∴∠ADB=180°-70°-40°=70°
故答案为:A.
4.解:连结AC,如图,
∵弧AC的度数为100°,
∴∠ABC=50°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°-∠ABC=90°-50°=40°,
∴∠D=∠BAC=40°.
故答案为:B.
5.解:连接OA,
∵⊙O的直径CD=20,OM:OD=3:5,
∴OD=10,OM=6,
∵AB⊥CD,
∴AM=
=
=8,
∴AB=2AM=16.
故答案为:C.
6.解:连接OA、OB,作BH⊥AC于H,如图,
∵AB=CD,
∴
=
,
∴∠CAD=∠ACB=45°,
∵∠BAD+∠BCD=180°,
∴∠ACD+∠ACB+∠CAD+∠BAC=180°,
∵∠ACD=
∠BAC
∴
∠BAC+45°+45°+∠BAC=180°,解得∠BAC=60°,
∵∠AOB=2∠ACB=90°,
∴△OAB为等腰直角三角形,
∴AB=
OA=6
,
在Rt△ABH中,∠BAH=60°,
∴AH=
AB=3
,BH=
AH=3
,
在Rt△BCH中,∵∠BCH=45°,
∴BC=
BH=
×3
=6
.
故答案为:A.
7.解:由题意:
=12,
∴S2=
×12×3=18,
∵S1=6×
×32=
,
∴S1>S2
,
故答案为:A.
8.解:连接OE,OF.
∵BD=12,AD:AB=1:2,
∴AD=4
,AB=8
,∠ABD=30°,
∴S△ABD=
=24
,S扇形DOE=
=6π,S△OEB=
=9
,
∵两个阴影的面积相等,
∴阴影面积=2×(24
﹣6π﹣9
)=30
﹣12π.
故答案为:C.
9.解:如图,作BM⊥EC于M.
?
∵CB=CE,
∴∠CBE=∠CEB,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠AEB=∠MEB,
∵∠A=∠BME=90°,BE=BE,
∴△BEA≌△BEM(AAS),
∴AE=EM,AB=BM.
∵∠BMH=∠GCH=90°,∠BHM=∠GHC,BM=AB=CG,
∴△BMH≌△GCH(AAS),
∴MH=CH,BH=HG,
∴EH=EM+MH=AE+CH,故①③符合题意,
∵∠AEB+∠ABE=90°,
∴2∠AEB+2∠ABE=180°,
∵∠DEC+∠AEC=180°,∠AEC=2∠AEB,
∴∠DEC+2∠AEB=180°,
∴∠DEC=2∠ABE,故②符合题意,
∵FH平分∠EFG,
∴∠EFH=45°,
∵∠FEH=90°,
∴AB=EF=EH,
∵EH>HM=CH,
∴CH<AB,故④不符合题意.
故答案为:C.
10.连接AC、BD、OF,AC与EF交于P点,则它们的交点为O点,如图,
∵正方形ABCD和等边△AEF都内接于圆O,
∴正方形ABCD和等边△AEF都是轴对称图形,直径AC是对称轴,
∴∠COF=60°,AC⊥BD,AC⊥EF,∠BCA=45°,
∴PE=PF=
EF=3,
在Rt△OPF中,OP=
OF=
OC,
∵OP=
PF=
,
∴PC=OP=
,
∵△PCG为等腰直角三角形,
∴PG=PC=
,
∴EG=PE﹣PG=3﹣
.
故答案为:B.
二、填空题
11.解:根据弧长公式:
,
故答案为:
.
12.解:过点
作
于
,连接
,如图,
则
,
在
中,
,
所以
与
之间的距离是3.
故答案为3.
13.解:∵AC=AD,∠A=30°,
∴∠ACD=∠ADC=75°,
∵AO=OC,
∴∠OCA=∠A=30°,
∴∠OCD=45°,即△OCE是等腰直角三角形,
在等腰Rt△OCE中,OC=2;
因此OE=
.
故答案为:
.
14.解:连接AD,
∵AB是直径,
∴∠ADB=90°,即AD⊥BC,
∵D为BC的中线,
∴△ABC是等腰三角形,
∴∠B=∠C=24°,
∴∠AOD=2∠B=48°,
∵AB=4,
∴半径为2,
∴S阴影=
,
故答案为:
.
15.解:连接OB,
∵AC是⊙O的直径,弦BD⊥AC,
∴BE=
BD=6cm,
在Rt△OEB中,OB2=OE2+BE2
,
即OB2=(OB﹣4)2+62
,
解得,OB=
,
则EC=AC﹣AE=9,
BC=
=
=3
,
∵OF⊥BC,
∴CF=
BC=
,
∴OF=
=
=
(cm).
故答案为:
.
16.解:y=x2-6x+8=(x-2)(x-4),故A(2,0),B(4,0),
根据垂径定理可知点M在AB的中垂线上,设M(3,a).
连接MC,过点M作ME∥x轴,过点B作BF垂直ME于点F,过点C作CE⊥ME于点E,
∵MB=MC,∠MBC=45°,
∴∠NCB=45°,
∴∠BMC=90°,
∵∠MEC=∠BFM=90°,
∴∠BMF=∠MCE,
∴△BMF≌△MCE,
∴ME=BF,MF=CE,
∵B(4,0),M(3,a).
∴CE=MF=1,EF=a-1,
∴C(4+a-1,a+1)即C(3+a,a+1),
由于点C在抛物线上,则有
a+1=(3+a)2-6(3+a)+8
解得a1=2,a2=-1,
根据圆心M在第一象限可得a2=-1不符合题意,故a=2,
∴C(5,3).
三、解答题
17.
解:如图所示,
△APQ的周长为2,即AP+AQ+PQ=2①,
正方形ABCD的边长是1,即AQ+QD=1,AP+PB=1,
∴AP+AQ+QD+PB=2②,
①﹣②得,PQ﹣QD﹣PB=0,
∴PQ=PB+QD
.
延长AB至M
,
使BM=DQ
.
连接CM
,
△CBM≌△CDQ(SAS),
∴∠BCM=∠DCQ
,
CM=CQ
,
∵∠DCQ+∠QCB=90°,
∴∠BCM+∠QCB=90°,即∠QCM=90°,
PM=PB+BM=PB+DQ=PQ
.
在△CPQ与△CPM中,
CP=CP
,
PQ=PM
,
CQ=CM
,
∴△CPQ≌△CPM(SSS),
∴∠PCQ=∠PCM=
∠QCM=45°.
18.
证明:连OC,OA,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴
,
∴AE=AC,
∴AE=AO
19.
(1)解:如图所示,△A1B1C1即为所求;
(2)解:如图所示,△A2B2C2即为所求;
(3)解:由勾股定理可得AC=
,
∴弧AA2的长=
.
20.
(1)证明∵BC平分∠ABD,
∴∠DBC=∠ABC
∴∠CAD=∠DBC
∴∠CAD=∠ABC
(2)解∵∠CAD=∠ABC,
∴
∵AD是⊙O的直径,AD=6,
∴
21.
(1)证明:∵
弦CD⊥AB
,∴
,
∴∠ADC=∠ACD,
∵
∠AGD=∠ACD,∴∠AGD=∠ADC,
∵四边形ABCG是圆内接四边形,
∴
∠FGC=∠ADC,∴
∠FGC=∠AGD;
(2)解:连接OD,∵CD⊥AB,CD=8,∴DE=CE=4,
在Rt△DOE中,DO2=OE2+ED2
,
∴DO2=(OD-2)2+42
,
解得OD=5,∴AE=10-2=8,
∴AD=.
22.
(1)解:过点P作x轴垂线PG,连接BP,CP,
∵P是正六边形ABCDEF的对称中心,CD=4,
∴BP=CP=4,G是CD的中点,
∴PG=2
,
∴P(4,2
),
∵P在反比例函数y=
上,
∴k=8
,
∴y=
,
连接AC交PB于G,则AC⊥PB,
由正六边形的性质得A(2,4
),
∴点A在反比例函数图象上
(2)解:过Q作QM⊥x轴于M,
∵六边形ABCDEF为正六边形,
∴∠EDM=60°,
设DM=b,则QM=
b,
∴Q(b+6,
b),
∵该反比例函数图象与DE交于点Q,
∴
b(b+6)=8
,
解得:b=﹣3+
,b=﹣3﹣
(不合题意舍去),
∴点Q的横坐标为3+
(3)解:连接AP,A(2,4
),B(0,2
),C(2,0),D(6,0),E(8,
),F(6,4
),
设正六边形向左平移m个单位,向上平移n个单位,则平移后点的坐标分别为
∴A(2﹣m,4
+n),B(﹣m,2
+n),C(2﹣m,n),D(6﹣m,n),E(8﹣m,2
+n),F(6﹣m,4
+n),
①将正六边形向左平移4个单位后,E(4,2
),F(2,4
);
则点E与F都在反比例函数图象上;
②将正六边形向右平移2个单位,再向上平移2
个单位后,C(4,2
),B(2,4
)
则点B与C都在反比例函数图象上
?
23.
(1)解:当y=0时,x2+3x﹣a2+a+2=0,
∴[x﹣(a﹣2)][x+(a+1)]=0,
∴x=a﹣2,或x=﹣a﹣1,
∵点A在点B左侧,
∴A(﹣a﹣1,0),B(a﹣2,0),
∴AB=a﹣2﹣(﹣a﹣1)=2a﹣1,
抛物线的对称轴为x=
=﹣
,即抛物线的对称轴为x=﹣
(2)解:存在,理由如下:
∵抛物线y=x2+3x﹣a2+a+2(a>1)的图象经过原点,a>1,
∴﹣a2+a+2=0,
解得:a=2,或a=﹣1(舍去),
∴a=2,
∴A(﹣3,0),B(0,0),y=x2+3x=(x+
)2﹣
,
∴E(﹣
,﹣
),
分情况讨论,如图2所示:
①若AB为平行四边形的边,则P点坐标为(
,﹣
)或(﹣
,﹣
);
②若AB为平行四边形的对角线,则P点坐标为(﹣
,﹣
);
综上所述,在平面内存在一点P,使得以A、B、E、P为顶点的四边形成为平行四边形,P点坐标为(
,﹣
)或(﹣
,﹣
)或(﹣
,﹣
)
(3)解:当a=3时,y=x2+3x﹣4,
此时A(﹣4,0),B(1,0),C(0,﹣4),
∴OA=4,OC=4,
设M(t,0),
∵将线段MC绕点M逆时针旋转90°得到线段MN,
∴OM=﹣t,
过点M作EF⊥x轴,过点N作NE⊥EF于点E,过点C作CF⊥EF于点F,如图3所示:
则∠MEN=∠CFM=90°,
由旋转的性质得:MN=MC,∠CMN=90°,
∴∠EMN+∠CMF=∠CMF+∠FCM=90°,
∴∠EMN=∠FCM,
在△MNE和△CMF中
,
∴△MNE≌△CMF(AAS),
∴MF=CF=OM=﹣t,EN=MF=OC=4,
∴点N的横坐标为Nx=4+t,点N的纵坐标为Ny=﹣t,
∴y=﹣x+4,
∴点N在直线l:y=﹣x+4上运动,
设直线l交x轴于点G,则G(4,0),
若使△ACN的周长最小,即使AN+CN最小,
∴作点A关于l的对称点A',连接A'C,A'N,
则AN=A'N,
当A'、N、C三点共线时,AN+CN最小=A'C,
由题意得:∠A'AO=45°,∠CAO=45°,
∴∠CAA'=90°,
∵G(4,0),
∴AG=OA+OG=8,AA'=
,
∵AC=
=
,
∴A'C=
=
,
∴A'C+AC=
+
,
∵△ACN的周长=AN+CN+AC,
∴△ACN周长的最小值为A'C+AC=4
+4
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
