第2章一元二次方程复习课

(共17张PPT)
学校门口建造一个面积为20平方米，长比宽多 1 米的长方形喷泉，问它的宽是多少？
解：
设这个喷泉的宽为x米，
x
则长为（x+1）米，
x+1
根据题意得：
x ( x+1) = 20
即 x 2 + x - 20 = 0
复习内容
一元二次方程的概念
一元二次方程的解法
一元二次方程根的判别式
一元二次方程的一般形式
任何一个关于x 一元二次方程,经过整理都可以化为以下形式
a x 2 + b x + c = 0
(a ≠ 0)
2
1
-3
1
1
-1
-7
1
0
3
0
-6
请填写下表:
说明：要确定一元二次方程的系数和常数项，必须先将方程化为一般形式。
二次项系数
一次项系数
常数项
做一做
1、判断下列方程是不是一元二次方程
（1）4x- x + =0 （2）3x - y -1=0
（3）ax +ｂx+c=0 （4）x + =0
是
不是
不是
不一定
2、已知关于x的方程（m -1）x +（m-1）x-m+1=0，当m 时是一元二次方程，当m=　　 时是一元一次方程。
3、已知x＝3是一元二次方程x2+(2m-1)x-m=0的一个根，则m= 　　
-1
≠±1
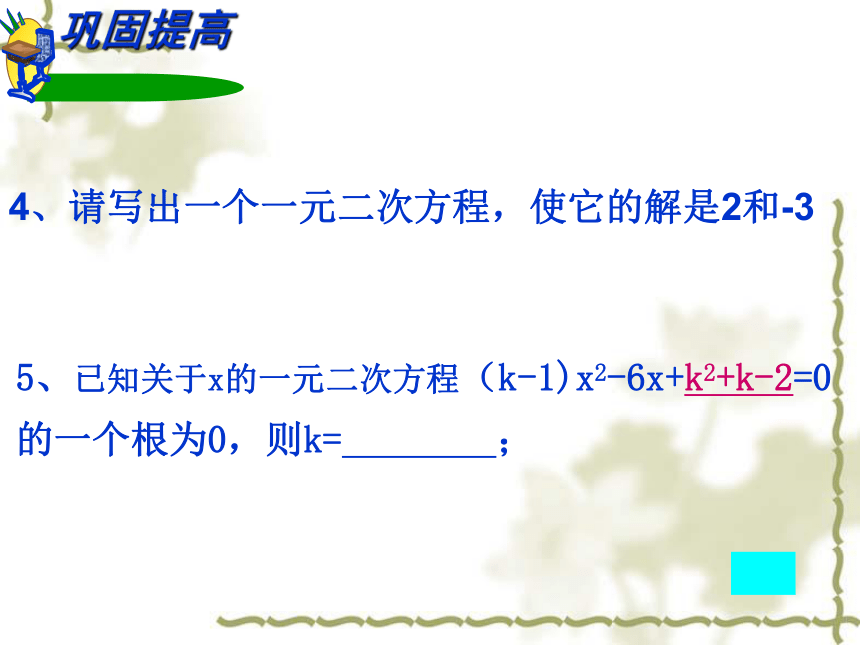
巩固提高
5、已知关于x的一元二次方程（k-1)x2-6x+k2+k-2=0的一个根为0，则k= ；
4、请写出一个一元二次方程，使它的解是2和-3
一元二次方程的解法
1.因式分解法。
2.开平方法。
3.配方法。
4.公式法
1.把二次项,一次项移到等号左边,常数项移到等号右边。
2.两边同加上一次项系数一半的平方。
请用四种方法解下列方程:
先考虑开平方法,
再用因式分解法;
最后才用公式法和配方法;
解决问题：
建造一个面积为20平方米，长比宽多 1 米的长方形喷泉，问它的宽是多少？
解：
设这个喷泉的宽为x米，
x
则长为（x+1）米，
x+1
根据题意得：
x ( x+1) = 20
即 x 2 + x - 20 = 0
解得:
答:这个长方形的喷泉的宽为4米。
经检验， 不符合题意，舍去。
用适当的方法解下列方程
（1）
（2）
（3）
（4）
问题:
用适当的方法解下列一元二次方程:
①: (x-2)2=9
②:
③: 2x2-1 = -3x
注意点:
ax2+bx+c=0(a≠0)有实数解的前提是:________
b2-4ac≥0
9(x-2)2- 4=0
2x2+3x+7 = 0
一元二次方程根的判别式
两不相等实根
两相等实根
无实根
一元二次方程
一元二次方程 根的判式是:
判别式的情况
根的情况
两个不相等实根
两个相等实根
无实根
知识聚焦
两者关系
例1：不解方程，判别下列方程的根的情况
（1）
（3）
（2）
当k取什么值时，已知关于x的方程：
（1）方程有两个不相等的实根；
（2）方程有两个相等的实根；（3）方程无实根；
解：△=
(1).当△>0 ，方程有两个不相等的实根, 8k+9 >0 , 即
(2).当△ = 0 ，方程有两个相等的实根, 8k+9 =0 , 即
(3).当△ <0 ，方程有没有实数根, 8k+9 <0 , 即
K＜
思考与探究
小结：
这节课你有哪些收获？
作业：作业本（一）复习题