1.5.3 三角形全等的判定——ASA同步训练(含解析)
文档属性
| 名称 | 1.5.3 三角形全等的判定——ASA同步训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 07:20:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册1.5 三角形全等的判定——ASA
一、单选题
1.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是(??? )
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
2.如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB,AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确(??? )?
A.?两人皆正确??????????????????B.?两人皆错误??????????????????C.?甲正确,乙错误??????????????????D.?甲错误,乙正确
3.如图,△ABC的面积为8cm2 , ∠B的平分线BP垂直AP于点P,则△PBC的面积为(??? )
A.?5cm2??? ?????????????????????????????????B.?4cm2?????????????????????????????????C.?3cm2?????????????????????????????????D.?2cm2
4.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°.
其中结论正确的个数是(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?0
二、填空题
5.如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是________.(填写一个即可,不得添加辅助线和字母)
6.如图,要测量池塘两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使A、C、E三点在一条直线上,这时测得________的长就等于AB的长,这样做的依据是________.
7.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以带那一块________.
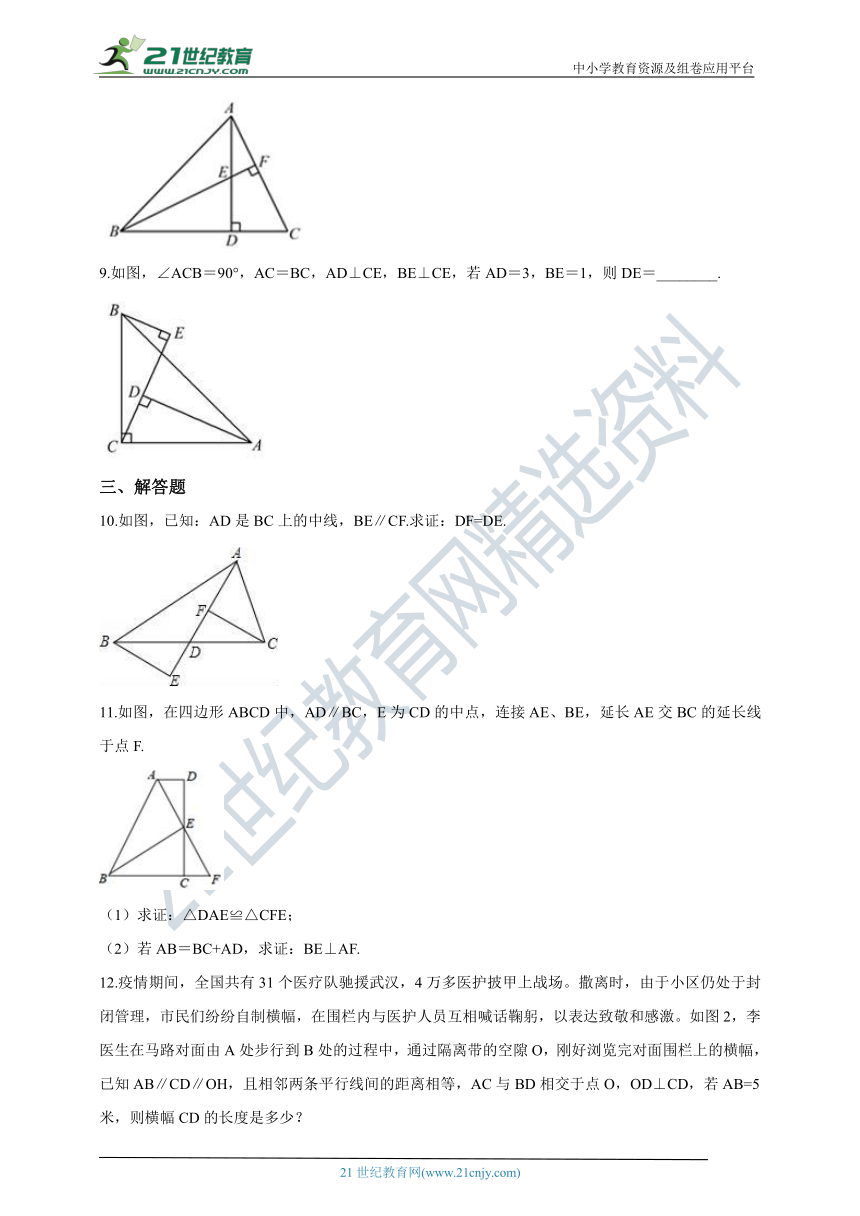
8.如图,在△ABC中,BF⊥AC 于点F,AD⊥BC 于点D ,BF 与AD 相交于点E.若AD=BD,BC=8cm,DC=3cm.则 AE= ________cm?.
???
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,若AD=3,BE=1,则DE=________.
三、解答题
10.如图,已知:AD是BC上的中线,BE∥CF.求证:DF=DE.
11.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
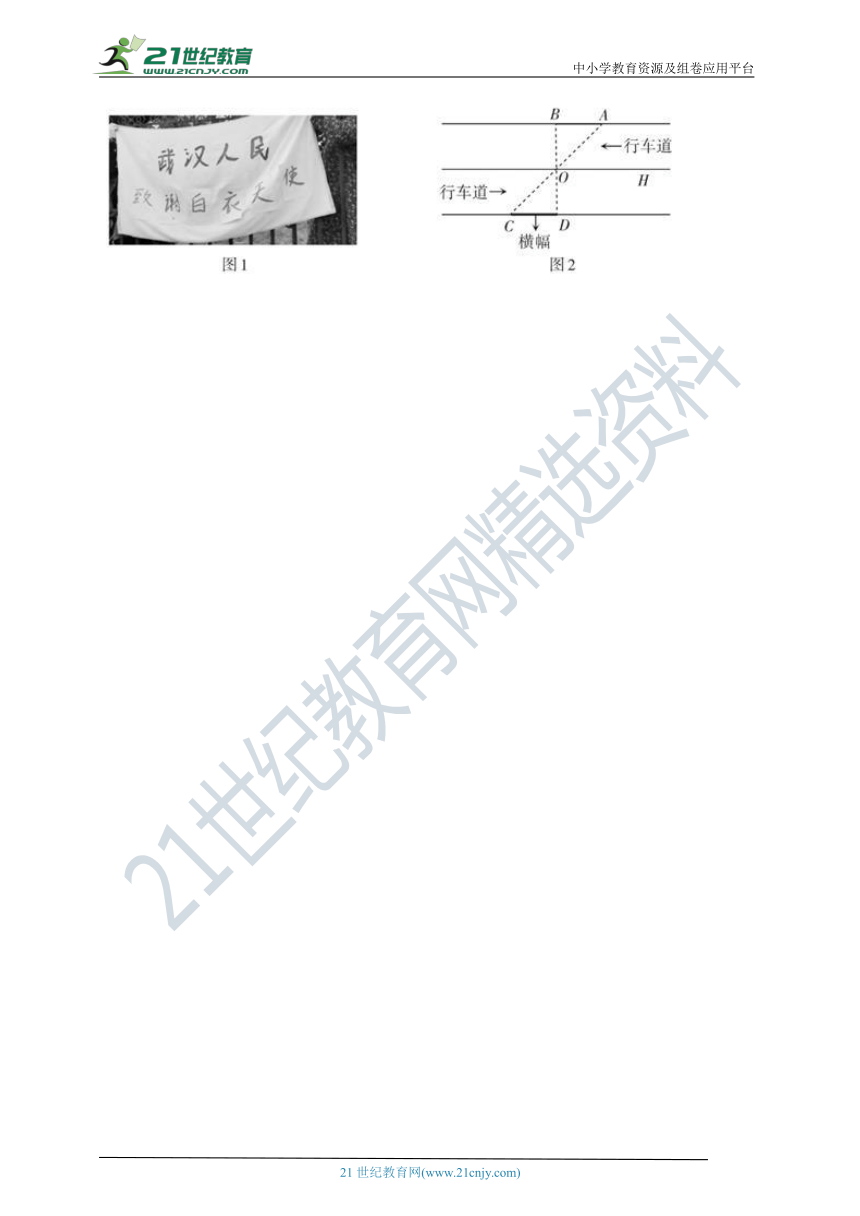
12.疫情期间,全国共有31个医疗队驰援武汉,4万多医护披甲上战场。撒离时,由于小区仍处于封闭管理,市民们纷纷自制横幅,在围栏内与医护人员互相喊话鞠躬,以表达致敬和感激。如图2,李医生在马路对面由A处步行到B处的过程中,通过隔离带的空隙O,刚好浏览完对面围栏上的横幅,已知AB∥CD∥OH,且相邻两条平行线间的距离相等,AC与BD相交于点O,OD⊥CD,若AB=5米,则横幅CD的长度是多少?
答案解析部分
一、单选题
1. C
考点:全等三角形的应用
解:由题意得:依据是角边角定理.
故答案为:C.
分析:因为一角残缺,但三角形的另外两个角是完整的,这两个角的夹边也是完好的,所以利用角边角定理判定三角形全等则可确定一个三角形的形状。
2. A
考点:三角形全等的判定
解:甲:如图
∵PQ垂直平分AD,
∴AP=PD,AQ=QD
在△APQ和△DPQ中
∴△APQ≌△DPQ(SSS),故甲正确;
乙、如图
∵PD∥AC,DQ∥AB,
∴∠PQD=∠APQ,∠DPQ=∠AQP
在△APQ和△DPQ中
∴△APQ≌△DPQ(ASA),故乙正确;
∴甲乙都正确.
故答案为:A.
分析:根据题意分别画出甲和乙两人的作法,利用线段垂直平分线的性质,可证得AP=PD,AQ=QD,再利用SSS可证得两三角形全等,可对甲作出判断;利用平行线的性质,可知∠PQD=∠APQ,∠DPQ=∠AQP,然后利用ASA可证两三角形全等,即可得出正确的选项。
3. B
考点:三角形的面积,全等三角形的判定与性质
解:如图,
∵BP平分∠ABC,
∴∠ABP=∠EBP
BP⊥AE,
∴∠APB=∠EPB=90°
在△ABP和△EBP中,
∴△ABP≌△EBP(ASA)
∴AP=PE
∴BP是△ABE的中线,CP是△ACE的中线,
∴S△BPE=S△ABE , S△CPE=S△ABE ,
∴S△PBC=S△BPE+S△CPE=S△ABE+S△ABE=S△ABC=×8=4.
故答案为:B.
分析:利用角平分线的定义和垂直的定义,易证∠ABP=∠EBP,∠APB=∠EPB,再利用ASA证明△ABP≌△EBP,从而可证得AP=PE,根据三角形中线分得的两个三角形的面积相等,可以推出S△PBC=S△ABC , 代入计算可求解。
4. C
考点:全等三角形的判定与性质
解:①
∴∠BAC+∠CAD=∠DAE+∠CAD ,
即∠BAD=∠CAE ,
∵在△BAD和△CAE中,
?
?∴BD=CE , 故①符合题意;②
?
?
?
?则BD⊥CE , 故②符合题意③∵△ABC为等腰直角三角形,
?
?
?
?故③符合题意;
故答案为:C.
分析:根据条件,易证:即可判断 ① ,根据全等三角形的性质,可知进而,可判断 ②?和 ③ ,即可得到答案.
二、填空题
5. ∠A=∠D
考点:三角形全等的判定
解:A=∠D,
理由是:∵∠ACD=∠BCE,
∴∠ACD+∠DCB=∠BCE+∠DCB,
∴∠ACB=∠DCE,
在△ACB和△DCE中 ,
∴△ACB≌△DCE(ASA),
故答案为:∠A=∠D.
分析:开放性的命题,答案不唯一,由已知条件可以得出∠ACB=∠DCE,又题干给出了 AC=DC ,根据三角形全等的判定方法再添加 ∠A=∠D或∠B=∠E或BC=EC 即可.
6. DE;ASA证明△ABC≌△EDC,全等三角形对应边相等
考点:全等三角形的判定与性质
解:根据题意可知:
∠B=∠D=90°,BC=CD,∠ACB=∠ECD,
即
∴△ABC≌△EDC(ASA),
∴AB=DE.
故答案为:DE.
分析:由对顶角相等,两个直角相等及BD=CD,可以判断两个三角形全等;所以AB=DE.
7. ③
考点:三角形全等的判定,全等三角形的应用
解:第①块,仅保留了原三角形的一个角和部分边,不符合全等三角形的判定方法;
第②块,仅保留了原三角形的一部分边,所以此块玻璃也不行;
第③块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故答案是:③.
分析:根据全等三角形的判定方法,在打碎的三块中可以采用排除法进行分析从而确定最后的答案.
8. 2.
考点:全等三角形的判定与性质
解:∵BF⊥AC于F,AD⊥BC于D,
∴∠CAD+∠C=90°,∠CBF+∠C=90°,
∴∠CAD=∠CBF,
∵在△ACD和△BED中,
∴△ACD≌△BED,(ASA)
∴DE=CD,
∴AE=AD-DE=BD-CD=BC-CD-CD=2;
故答案为2.
分析:易证∠CAD=∠CBF,即可求证△ACD≌△BED,可得DE=CD,即可求得AE的长,即可解题.
9. 2
考点:全等三角形的判定与性质
解:∵∠ACB=90°
∴∠BCE+∠ACE=90°
又∵AD⊥CE,BE⊥CE
∴∠E+∠ADC=90°
∴∠DAC+∠ACE=90°
∴∠BCE=∠DAC
又∵AC=BC
∴△BEC≌△CDA
∴EC=AD=3,CD=BE=1
∴ED=EC-CD=3-1=2.
分析:先利用余角关系证明∴∠BCE=∠DAC,即可用“ASA”证得△BEC≌△CDA,然后利用全等三角形的对应边相等证得EC=AD=3,CD=BE=1,则可由ED=EC-CD得解。
三、解答题
10. 证明:CF∥BE,
∴∠FCD=∠EBD,
∵AD是BC上的中线,
∴BD=DC,
在△CDF和△BDE中,
?
∴△CDF≌△BDE(ASA),
∴DF=DE.
考点:全等三角形的判定与性质
【解析】分析:根据平行线性质得出∠FCD=∠EBD,由BD=DC,∠CDF=∠BDE,根据ASA推出△CDF≌△BDE,即可得出结论.
11. (1)证明:∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA);
(2)解:由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,
在△ABE与△FBE中,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AF.
考点:全等三角形的判定与性质
【解析】分析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE;(2)由(1)知△ADE≌△FCE,得到AE=EF,AD=CF,由于AB=BC+AD,等量代换得到AB=BC+CF,即AB=BF,证得△ABE≌△FBE,即可得到结论.
12. 解:∵BD⊥CD,AB∥CD,
∴BD⊥AB
∴∠ABO=∠CDO=90°
相邻两条平行线间的距离相等,
∴OB=OD,
在△ABO和△CDO中,
∴△ABO≌△CDO(ASA)
∴CD=AB=5
答:横幅CD的长度为5米
考点:全等三角形的判定与性质
【解析】分析:利用平行线的性质,根据ASA判定定理证明三角形全等,根据全等三角形的性质得出结果。
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册1.5 三角形全等的判定——ASA
一、单选题
1.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是(??? )
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
2.如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB,AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确(??? )?
A.?两人皆正确??????????????????B.?两人皆错误??????????????????C.?甲正确,乙错误??????????????????D.?甲错误,乙正确
3.如图,△ABC的面积为8cm2 , ∠B的平分线BP垂直AP于点P,则△PBC的面积为(??? )
A.?5cm2??? ?????????????????????????????????B.?4cm2?????????????????????????????????C.?3cm2?????????????????????????????????D.?2cm2
4.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°.
其中结论正确的个数是(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?0
二、填空题
5.如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是________.(填写一个即可,不得添加辅助线和字母)
6.如图,要测量池塘两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使A、C、E三点在一条直线上,这时测得________的长就等于AB的长,这样做的依据是________.
7.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以带那一块________.
8.如图,在△ABC中,BF⊥AC 于点F,AD⊥BC 于点D ,BF 与AD 相交于点E.若AD=BD,BC=8cm,DC=3cm.则 AE= ________cm?.
???
9.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,若AD=3,BE=1,则DE=________.
三、解答题
10.如图,已知:AD是BC上的中线,BE∥CF.求证:DF=DE.
11.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
12.疫情期间,全国共有31个医疗队驰援武汉,4万多医护披甲上战场。撒离时,由于小区仍处于封闭管理,市民们纷纷自制横幅,在围栏内与医护人员互相喊话鞠躬,以表达致敬和感激。如图2,李医生在马路对面由A处步行到B处的过程中,通过隔离带的空隙O,刚好浏览完对面围栏上的横幅,已知AB∥CD∥OH,且相邻两条平行线间的距离相等,AC与BD相交于点O,OD⊥CD,若AB=5米,则横幅CD的长度是多少?
答案解析部分
一、单选题
1. C
考点:全等三角形的应用
解:由题意得:依据是角边角定理.
故答案为:C.
分析:因为一角残缺,但三角形的另外两个角是完整的,这两个角的夹边也是完好的,所以利用角边角定理判定三角形全等则可确定一个三角形的形状。
2. A
考点:三角形全等的判定
解:甲:如图
∵PQ垂直平分AD,
∴AP=PD,AQ=QD
在△APQ和△DPQ中
∴△APQ≌△DPQ(SSS),故甲正确;
乙、如图
∵PD∥AC,DQ∥AB,
∴∠PQD=∠APQ,∠DPQ=∠AQP
在△APQ和△DPQ中
∴△APQ≌△DPQ(ASA),故乙正确;
∴甲乙都正确.
故答案为:A.
分析:根据题意分别画出甲和乙两人的作法,利用线段垂直平分线的性质,可证得AP=PD,AQ=QD,再利用SSS可证得两三角形全等,可对甲作出判断;利用平行线的性质,可知∠PQD=∠APQ,∠DPQ=∠AQP,然后利用ASA可证两三角形全等,即可得出正确的选项。
3. B
考点:三角形的面积,全等三角形的判定与性质
解:如图,
∵BP平分∠ABC,
∴∠ABP=∠EBP
BP⊥AE,
∴∠APB=∠EPB=90°
在△ABP和△EBP中,
∴△ABP≌△EBP(ASA)
∴AP=PE
∴BP是△ABE的中线,CP是△ACE的中线,
∴S△BPE=S△ABE , S△CPE=S△ABE ,
∴S△PBC=S△BPE+S△CPE=S△ABE+S△ABE=S△ABC=×8=4.
故答案为:B.
分析:利用角平分线的定义和垂直的定义,易证∠ABP=∠EBP,∠APB=∠EPB,再利用ASA证明△ABP≌△EBP,从而可证得AP=PE,根据三角形中线分得的两个三角形的面积相等,可以推出S△PBC=S△ABC , 代入计算可求解。
4. C
考点:全等三角形的判定与性质
解:①
∴∠BAC+∠CAD=∠DAE+∠CAD ,
即∠BAD=∠CAE ,
∵在△BAD和△CAE中,
?
?∴BD=CE , 故①符合题意;②
?
?
?
?则BD⊥CE , 故②符合题意③∵△ABC为等腰直角三角形,
?
?
?
?故③符合题意;
故答案为:C.
分析:根据条件,易证:即可判断 ① ,根据全等三角形的性质,可知进而,可判断 ②?和 ③ ,即可得到答案.
二、填空题
5. ∠A=∠D
考点:三角形全等的判定
解:A=∠D,
理由是:∵∠ACD=∠BCE,
∴∠ACD+∠DCB=∠BCE+∠DCB,
∴∠ACB=∠DCE,
在△ACB和△DCE中 ,
∴△ACB≌△DCE(ASA),
故答案为:∠A=∠D.
分析:开放性的命题,答案不唯一,由已知条件可以得出∠ACB=∠DCE,又题干给出了 AC=DC ,根据三角形全等的判定方法再添加 ∠A=∠D或∠B=∠E或BC=EC 即可.
6. DE;ASA证明△ABC≌△EDC,全等三角形对应边相等
考点:全等三角形的判定与性质
解:根据题意可知:
∠B=∠D=90°,BC=CD,∠ACB=∠ECD,
即
∴△ABC≌△EDC(ASA),
∴AB=DE.
故答案为:DE.
分析:由对顶角相等,两个直角相等及BD=CD,可以判断两个三角形全等;所以AB=DE.
7. ③
考点:三角形全等的判定,全等三角形的应用
解:第①块,仅保留了原三角形的一个角和部分边,不符合全等三角形的判定方法;
第②块,仅保留了原三角形的一部分边,所以此块玻璃也不行;
第③块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故答案是:③.
分析:根据全等三角形的判定方法,在打碎的三块中可以采用排除法进行分析从而确定最后的答案.
8. 2.
考点:全等三角形的判定与性质
解:∵BF⊥AC于F,AD⊥BC于D,
∴∠CAD+∠C=90°,∠CBF+∠C=90°,
∴∠CAD=∠CBF,
∵在△ACD和△BED中,
∴△ACD≌△BED,(ASA)
∴DE=CD,
∴AE=AD-DE=BD-CD=BC-CD-CD=2;
故答案为2.
分析:易证∠CAD=∠CBF,即可求证△ACD≌△BED,可得DE=CD,即可求得AE的长,即可解题.
9. 2
考点:全等三角形的判定与性质
解:∵∠ACB=90°
∴∠BCE+∠ACE=90°
又∵AD⊥CE,BE⊥CE
∴∠E+∠ADC=90°
∴∠DAC+∠ACE=90°
∴∠BCE=∠DAC
又∵AC=BC
∴△BEC≌△CDA
∴EC=AD=3,CD=BE=1
∴ED=EC-CD=3-1=2.
分析:先利用余角关系证明∴∠BCE=∠DAC,即可用“ASA”证得△BEC≌△CDA,然后利用全等三角形的对应边相等证得EC=AD=3,CD=BE=1,则可由ED=EC-CD得解。
三、解答题
10. 证明:CF∥BE,
∴∠FCD=∠EBD,
∵AD是BC上的中线,
∴BD=DC,
在△CDF和△BDE中,
?
∴△CDF≌△BDE(ASA),
∴DF=DE.
考点:全等三角形的判定与性质
【解析】分析:根据平行线性质得出∠FCD=∠EBD,由BD=DC,∠CDF=∠BDE,根据ASA推出△CDF≌△BDE,即可得出结论.
11. (1)证明:∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA);
(2)解:由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,
在△ABE与△FBE中,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AF.
考点:全等三角形的判定与性质
【解析】分析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE;(2)由(1)知△ADE≌△FCE,得到AE=EF,AD=CF,由于AB=BC+AD,等量代换得到AB=BC+CF,即AB=BF,证得△ABE≌△FBE,即可得到结论.
12. 解:∵BD⊥CD,AB∥CD,
∴BD⊥AB
∴∠ABO=∠CDO=90°
相邻两条平行线间的距离相等,
∴OB=OD,
在△ABO和△CDO中,
∴△ABO≌△CDO(ASA)
∴CD=AB=5
答:横幅CD的长度为5米
考点:全等三角形的判定与性质
【解析】分析:利用平行线的性质,根据ASA判定定理证明三角形全等,根据全等三角形的性质得出结果。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
