1.5.4 三角形全等的判定——AAS和角平分线同步训练(含解析)
文档属性
| 名称 | 1.5.4 三角形全等的判定——AAS和角平分线同步训练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册1.5 三角形全等的判定——AAS和角平分线
一、单选题
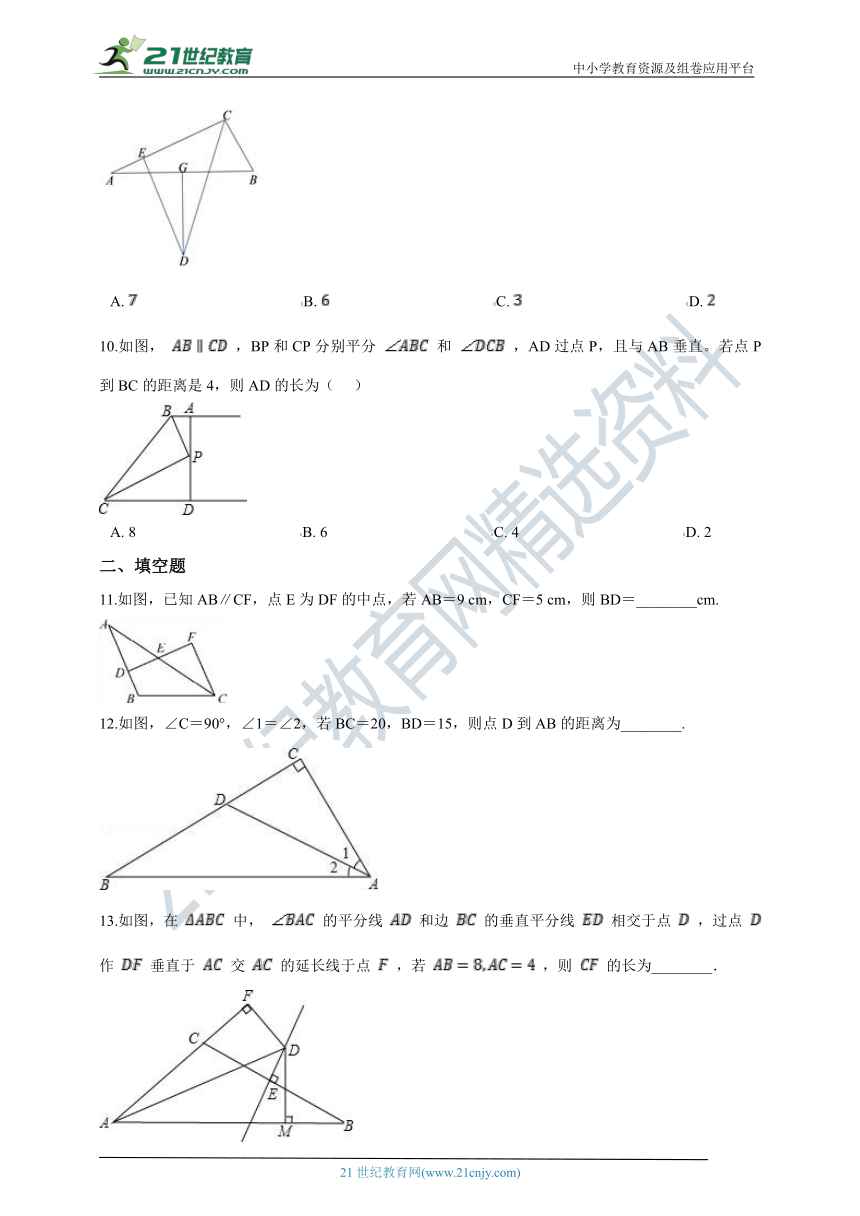
1.已知△ABC , 两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB , AC上,且这组对应边所对的顶点重合于点M , 点M一定在(??? )
A.?∠A的平分线上???????????B.?AC边的高上??????????????C.?BC边的垂直平分线上??????????????D.?AB边的中线上
2.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=8,BD=10,则点D到BC的距离是( )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
3.如图,在 中, , ,如果 平分 ,那么 的度数是(??? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
4.如图,BD是△ABC的角平分线,DE是BC的垂直平分线,∠A=90°,AD=2,则CD的长为(??? )
A.?3 ?????????????????????????????????????????B.?6?????????????????????????????????????????C.?5?????????????????????????????????????????D.?4
5.现要在一块三角形的草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(???? )
A.?△ABC的三条中线的交点?????????????????????????????????????B.?△ABC三边的垂直平分线的交点
C.?△ABC三条角平分线的交点??????????????????????????????????D.?△ABC三条高所在直线的交点
6.在证明等腰三角形的判定定理“等角对等边”,即“如图,已知:∠B=∠C,求证:AB=AC”时,小明作了如下的辅助线,下列对辅助线的描述正确的有(?? )
①作∠BAC的平分线AD交BC于点D②取BC边的中点D,连接AD③过点A作AD⊥BC,垂足为点D④作BC边的垂直平分线AD,交BC于点D
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
7.若射线OC在∠AOB内部,则下列①∠AOC=∠BOC;②∠AOB=2∠AOC;③∠AOB=∠AOC+∠BOC;④∠BOC= ∠AOB;能判定射线OC是∠AOB的角平分线的有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
8.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=8,则四边形ABCD的面积为(?? )
A.?32?????????????????????????????????????????B.?24?????????????????????????????????????????C.?40?????????????????????????????????????????D.?36
9.如图, 中, 的垂直平分线 交 的平分线 于点 ,过 作 于点 ,若 , ,则 (? )
A.????????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.?
10.如图, ,BP和CP分别平分 和 ,AD过点P,且与AB垂直。若点P到BC的距离是4,则AD的长为(??? )
A.?8???????????????????????????????????????????B.?6???????????????????????????????????????????C.?4???????????????????????????????????????????D.?2
二、填空题
11.如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=________cm.
12.如图,∠C=90°,∠1=∠2,若BC=20,BD=15,则点D到AB的距离为________.
13.如图,在 中, 的平分线 和边 的垂直平分线 相交于点 ,过点 作 垂直于 交 的延长线于点 ,若 ,则 的长为________.
14.如图,OP平分∠AOB,PB⊥OB,PB=2cm,则点P到OA的距离是________cm.
15.如图,△ABC的角平分线交于点P,已知AB,BC,CA的长分别为5,7,6,则S△ABP∶S△BPC∶S△APC=________.
三、解答题
16.如图,已知CE⊥AB于E,BF⊥AC于F,BF交CE于D点,且AB=AC.
(1)求证:△ABF≌△ACE.
(2)求证:A点在∠EDF的平分线上.
17.已知O是AB上的一点,从O点引出射线OC、OE、OD , 其中OE平分∠BOC .
(1)如图1,若∠COD是直角,∠DOE=15°,∠AOC=________°;
(2)如图1,若∠AOC=∠BOD , ∠DOE=15°,求∠AOC的度数;
(3)将图1中的∠COD(∠COD仍是直角)绕顶点O顺时针旋转至图2的位置,若∠AOC=α,∠DOE=β,请猜想α与β之间存在什么样的数量关系,写出你的结论,并说明理由.
18.如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.
(1)如图1,过F点作FD⊥AC交AC于D点,求证:EC+CD=DF;
(2)如图2,连接BF交AC于G点,若 =3,求证:E点为BC中点;
(3)当E点在射线CB上,连接BF与直线AC交于G点,若 ,则 =________
答案解析部分
一、单选题
1. A
考点:角平分线的性质
解:作射线AM,由题意得,MG=MH,MG⊥AB,MH⊥AC,∴AM平分∠BAC,
故答案为:A.
分析:根据角平分线的判定定理结合已知条件即可解答.
2. B
考点:角平分线的性质
解:D作DE⊥BC于点E,如图所示,
在Rt△ABD中, ,
∵BD平分∠ABC,由角平分线的性质可得DE=AD=6,
故答案为:B.
分析:在Rt△ABD中,利用勾股定理可求AD,再过D作DE⊥BC于点E,由角平分线上的点到角两边的距离相等可得DE=AD.
3. C
考点:三角形内角和定理,三角形的外角性质,角平分线的性质
解:
?
平分 ,
?
?
故答案为:C.
分析:根据三角形的内角和求解 利用角平分线的性质与三角形的外角的性质可得答案
4. D
考点:角平分线的性质,线段垂直平分线的性质
解:∵ED为BC的垂直平分线
∴DB=DC
∴∠C=∠DBC
∵BD为△ABCB的角平分线
∴∠ABD=∠DBC
∴∠C=∠DBC=∠ABD=30°
∵DA⊥BA,DE⊥BC
∴DE=AD=2
∴CD=2ED=2AD=4
故答案为:D.
分析:根据线段垂直平分线的性质以及角平分线的性质,即可得到DE=AD=2,求出CD的长度即可。
5. C
考点:角平分线的性质
解:∵角平分线上的点到这个角两边的距离相等
∴凉亭的位置应选在△ABC三条角平分线的交点.
故答案为:C.
分析:利用角平分线的性质求解即可。
6. B
考点:三角形全等的判定
解:①作∠BAC的平分线AD交BC于点D,可得 (AAS)则△ABD≌△ACD,即可得AB=AC,故①符合题意;
②取BC边的中点D,连接AD,得BD=CD,AD=AD,∠B=∠C,根据这些条件不能判断△ABD≌△ACD,故②不符合题意;
③过点A作AD⊥BC,垂足为点D,得 (AAS)则△ABD≌△ACD,即可得AB=AC,故③符合题意;
④作BC边的垂直平分线AD,交BC于点D,过已知点不能作出已知线段的垂直平分线,辅助线作法不符合题意,故④不符合题意;
故答案为:B.
分析:根据已知和作辅助线所得的条件,对每一种方法进行分析,看能否判定△ABD≌△ACD即可.
7. C
考点:角平分线的性质
解:①∵∠AOC=∠BOC
∴OC平分∠AOB,即OC为∠AOB的角平分线,正确;
②∵∠AOC=∠AOB
∴∠AOB=2∠AOC=∠AOC+∠BOC
∴∠AOC=∠BOC
∴OC平分∠AOB,即OC为∠AOB的平分线。
③∵∠AOC+∠BOC=∠AOB
∴假设∠AOC=30°,∠BOC=40°,,∠AOB=70°,但是OC不是∠AOB的平分线;④∵∠AOB=2∠BOC=∠AOC+∠BOC
∴∠AOC=∠BOC
∴OC平分∠AOB,即OC为∠AOB的角平分线,正确;
故答案为:C.
分析:根据角平分线的判定和性质,分别进行判断得到答案即可。
8. A
考点:全等三角形的判定与性质
解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N;
∵∠BAD=∠BCD=90°
∴四边形AMCN为矩形,∠MAN=90°;
∵∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
?
∴△ABM≌△ADN(AAS),
∴AM=AN(设为a);△ABM与△ADN的面积相等;
∴四边形ABCD的面积=正方形AMCN的面积;
由勾股定理得:AC2=AM2+MC2 , 而AC=8;
∴2a2=64,a2=32,
故答案为:A.
分析:作辅助线;证明△ABM≌△ADN,得到AM=AN,△ABM与△ADN的面积相等;求出正方形AMCN的面积即可解决问题.
9. C
考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
解:如图, 连接BD、AD,过点D作DF⊥CB于点F.
∵ 的垂直平分线 交 的平分线 于点 ,DE⊥AC,DF⊥BC,
∴BD=AD,DE=DF.∴Rt△AED≌Rt△BFD.
∴BF=AE.
又∵∠ECD=∠FCD,∠CED=∠CFD,CA=CA,∴Rt△CED≌Rt△CFD,
∴CE=CF,
设AE的长度为x,则CE=10-x,CF=CB+BF= CB+AE= 4+x,
∴可列方程10-x=4+x,x=3,∴AE=3;
故答案为:C.
分析:连接BD、AD,过点D作DF⊥CB于点F,利用角平分线及线段垂直平分线的性质可求出BD=AD,DE=DF,依据HL定理可判断出Rt△AED≌Rt△BFD,根据全等三角形的性质即可得出BF=AE,再运用AAS定理可证得Rt△CED≌Rt△CFD,证出CE=CF,设AE的长度为x,根据CE=CF列方程求解即可.
10. A
考点:角平分线的性质
解:过点P作PE⊥BC于E.
∵AB∥CD,PA⊥AB,∴PD⊥CD.
∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE,∴PE=PA=PD.
∵PE=4,∴PA=PD=4,∴AD=PA+PD=8.
故答案为:A.
分析:过点P作PE⊥BC于E,根据角平分线上的点到角的两边的距离相等可得PA=PE,PD=PE,那么PE=PA=PD,又PE=4,进而求出AD的长.
二、填空题
11. 4
考点:全等三角形的判定与性质
解:∵AB∥CF,
∴∠A=∠ACF,
在△AED和△CEF中
,
∴△AED≌△CEF(AAS),
∴FC=AD=5cm,
∴BD=AB-AD=9-5=4(cm).
故答案为:4.
分析:根据二直线平行,内错角相等得出∠A=∠ACF,从而利用AAS判断出△AED≌△CEF,根据全等三角形的对应边相等得出FC=AD=5cm,从而根据BD=AB-AD即可算出答案.
12. 5
考点:角平分线的性质
解:作DE⊥AB于E,
∵BC=20,BD=15,
∴CD=20﹣15=5,
∵∠1=∠2,∠C=90°,DE⊥AB,
∴DE=CD=5.
故答案是:5.
分析:作DE⊥AB于E,根据角平分线上的点到角两边的距离相等即可得出DE=CD=5.
13.
考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
解:如图,连接CD,DB,作DM⊥AB于一点M,
∵AD平分∠A,
∴ ,
在△AFD和△AMD中, ,
∴△AFD≌△AMD(AAS),
∴AF=AM,
∵DE垂直平分线BC,
∴CD=BD(线段垂直平分线上的点到线段两端点距离相等),
∵AD平分∠A,DF⊥AC,DM⊥AB,
∴DF=DM(角平分线上的点到角的两边距离相等)
∵∠AFD=∠DMB=90°,
∴Rt△CDF≌Rt△BDM(HL),
∴BM=CF,
∵ ,
,
又∵ ,
∴ ,
∴ ,
故答案为: .
分析:根据角平分线的性质结合全等三角形的判定定理得出△AFD≌△AMD,即可得出AF=AM,再利用线段垂直平分线的性质得出CD=BD,根据HL得出Rt△CDF≌Rt△BDM,即可得出CF=BM,即可得出答案.
14. 2
考点:角平分线的性质
解:过点P作PD⊥OA于点D,
∵OP平分∠AOB,PB⊥OB,PB=2cm,
∴PD=PB=2cm,
故答案为2.
分析:过点P作PD⊥OA于点D,根据角平分线上的点到角的两边的距离相等可得PD=PB,从而得解.
15. 5:7:6
考点:三角形的面积,角平分线的性质
解:如图,过点P作PD⊥AB于点D,PE⊥BC,PF⊥AC,
∵△ABC的角平分线交于点P,
∴PD=PE=PF.
∵S△ABP= AB PD,S△BCP= BC PE,S△ACP= AC PF,
∴S△ABP∶S△BPC∶S△APC= AB PD: BC PE: AC PF=AB:BC:AC=5:7:6.
分析:如图,过点P作PD⊥AB于点D,PE⊥BC,PF⊥AC,根据角平分线上的点到角两边的距离相等得出PD=PE=PF,根据根据三角形的面积计算方法,由等高三角形的面积之比就等于底之比即可得出答案.
三、解答题
16. (1)证明:∵CE⊥AB,BF⊥AC,
∴∠CEA=90°,∠BFA=90°,
在△ABF和△ACE中, ,
∴△ABF≌△ACE(AAS);
(2)证明:∵△ABF≌△ACE,
∴AF=AE,
又∵AF⊥DF,AE⊥DE,
∴A点在∠EDF的平分线上.
考点:全等三角形的判定与性质
【解析】分析:(1)根据AAS可直接证明△ABF≌△ACE;(2)由△ABF≌△ACE可得AF=AE,结合AF⊥DF,AE⊥DE可得A点在∠EDF的平分线上.
17. (1)30°
(2)解:设∠AOC为x°,则∠BOD为x°,
则∠BOE=x+15,∠BOC=2x+30
∠BOC+∠AOC=180
2x+15+x=180
x=50°,∠AOC=50°
(3)解:α=2β,
理由如下:
∵ ∠COD是直角,∠DOE=β,
∴ ∠COE=∠COD﹣∠DOE=90°﹣β,
∵ OE平分∠BOC ,
∴ ∠BOC=2∠COE=2(90°﹣β),
∵ ∠AOC+∠BOC=180°,
∴ α+2(90°﹣β)=180°,
∴ α=2β
考点:角平分线的性质
【解析】分析:(1)根据∠DOE的度数以及∠COD为直角,即可得到∠COE的度数,根据OE为∠COB的平分线,根据平角的性质得到∠AOC的度数即可;
(2)根据题意,可以设∠AOC=∠BOD为x°,根据角之间的等量关系进行等量代换,根据平角的性质求出∠AOC的度数即可;
(3)根据直角的性质,结合角平分线的性质,即可得到∠BOC的度数,由平角的性质,即可得到α与β的关系。
18. (1)证明:如图1,
∵∠FAD+∠CAE=90°,∠FAD+∠F=90°,
∴∠CAE=∠AFD,
在△ADF和△ECA中, ,
∴△ADF≌△ECA(AAS),
∴AD=CD,FD=AC,
∴CE+CD=AD+CD=AC=FD,即EC+CD=DF;
(2)证明:如图2,
过F点作FD⊥AC交AC于D点,
∵△ADF≌△ECA,
∴FD=AC=BC,
在△FDG和△BCG中, ,
∴△FDG≌△BCG(AAS),
∴GD=CG,
∵ =3
∴
∴ ,
∵AD=CE,AC=BC
∴ ,
∴E点为BC中点;
(3)
考点:全等三角形的判定与性质
解:过F作FD⊥AG的延长线交于点D,如图3,
∵ ,BC=AC,CE=CB+BE,
∴ ,
由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,
∴CG=GD,AD=CE,
∴ ,
∴ .
分析:(1)通过全等三角形△ADF≌△EDA的对应边相等得到:AD=CD,FD=AC,则利用等量代换和图形中相关线段间的和差关系证得结论;(2)过F点作FD⊥AC交AC于D点,根据(1)中结论可得FD=AC=BC,即可证明△FGD≌△BCD,可得DG=CG,根据 =3可证 ,根据AD=CE,AC=BC,即可解题;(3)过F作FD⊥AG的延长线交于点D,易证 ,由(1)(2)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得 的值,即可解题.
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册1.5 三角形全等的判定——AAS和角平分线
一、单选题
1.已知△ABC , 两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB , AC上,且这组对应边所对的顶点重合于点M , 点M一定在(??? )
A.?∠A的平分线上???????????B.?AC边的高上??????????????C.?BC边的垂直平分线上??????????????D.?AB边的中线上
2.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=8,BD=10,则点D到BC的距离是( )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
3.如图,在 中, , ,如果 平分 ,那么 的度数是(??? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
4.如图,BD是△ABC的角平分线,DE是BC的垂直平分线,∠A=90°,AD=2,则CD的长为(??? )
A.?3 ?????????????????????????????????????????B.?6?????????????????????????????????????????C.?5?????????????????????????????????????????D.?4
5.现要在一块三角形的草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(???? )
A.?△ABC的三条中线的交点?????????????????????????????????????B.?△ABC三边的垂直平分线的交点
C.?△ABC三条角平分线的交点??????????????????????????????????D.?△ABC三条高所在直线的交点
6.在证明等腰三角形的判定定理“等角对等边”,即“如图,已知:∠B=∠C,求证:AB=AC”时,小明作了如下的辅助线,下列对辅助线的描述正确的有(?? )
①作∠BAC的平分线AD交BC于点D②取BC边的中点D,连接AD③过点A作AD⊥BC,垂足为点D④作BC边的垂直平分线AD,交BC于点D
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
7.若射线OC在∠AOB内部,则下列①∠AOC=∠BOC;②∠AOB=2∠AOC;③∠AOB=∠AOC+∠BOC;④∠BOC= ∠AOB;能判定射线OC是∠AOB的角平分线的有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
8.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=8,则四边形ABCD的面积为(?? )
A.?32?????????????????????????????????????????B.?24?????????????????????????????????????????C.?40?????????????????????????????????????????D.?36
9.如图, 中, 的垂直平分线 交 的平分线 于点 ,过 作 于点 ,若 , ,则 (? )
A.????????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.?
10.如图, ,BP和CP分别平分 和 ,AD过点P,且与AB垂直。若点P到BC的距离是4,则AD的长为(??? )
A.?8???????????????????????????????????????????B.?6???????????????????????????????????????????C.?4???????????????????????????????????????????D.?2
二、填空题
11.如图,已知AB∥CF,点E为DF的中点,若AB=9 cm,CF=5 cm,则BD=________cm.
12.如图,∠C=90°,∠1=∠2,若BC=20,BD=15,则点D到AB的距离为________.
13.如图,在 中, 的平分线 和边 的垂直平分线 相交于点 ,过点 作 垂直于 交 的延长线于点 ,若 ,则 的长为________.
14.如图,OP平分∠AOB,PB⊥OB,PB=2cm,则点P到OA的距离是________cm.
15.如图,△ABC的角平分线交于点P,已知AB,BC,CA的长分别为5,7,6,则S△ABP∶S△BPC∶S△APC=________.
三、解答题
16.如图,已知CE⊥AB于E,BF⊥AC于F,BF交CE于D点,且AB=AC.
(1)求证:△ABF≌△ACE.
(2)求证:A点在∠EDF的平分线上.
17.已知O是AB上的一点,从O点引出射线OC、OE、OD , 其中OE平分∠BOC .
(1)如图1,若∠COD是直角,∠DOE=15°,∠AOC=________°;
(2)如图1,若∠AOC=∠BOD , ∠DOE=15°,求∠AOC的度数;
(3)将图1中的∠COD(∠COD仍是直角)绕顶点O顺时针旋转至图2的位置,若∠AOC=α,∠DOE=β,请猜想α与β之间存在什么样的数量关系,写出你的结论,并说明理由.
18.如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.
(1)如图1,过F点作FD⊥AC交AC于D点,求证:EC+CD=DF;
(2)如图2,连接BF交AC于G点,若 =3,求证:E点为BC中点;
(3)当E点在射线CB上,连接BF与直线AC交于G点,若 ,则 =________
答案解析部分
一、单选题
1. A
考点:角平分线的性质
解:作射线AM,由题意得,MG=MH,MG⊥AB,MH⊥AC,∴AM平分∠BAC,
故答案为:A.
分析:根据角平分线的判定定理结合已知条件即可解答.
2. B
考点:角平分线的性质
解:D作DE⊥BC于点E,如图所示,
在Rt△ABD中, ,
∵BD平分∠ABC,由角平分线的性质可得DE=AD=6,
故答案为:B.
分析:在Rt△ABD中,利用勾股定理可求AD,再过D作DE⊥BC于点E,由角平分线上的点到角两边的距离相等可得DE=AD.
3. C
考点:三角形内角和定理,三角形的外角性质,角平分线的性质
解:
?
平分 ,
?
?
故答案为:C.
分析:根据三角形的内角和求解 利用角平分线的性质与三角形的外角的性质可得答案
4. D
考点:角平分线的性质,线段垂直平分线的性质
解:∵ED为BC的垂直平分线
∴DB=DC
∴∠C=∠DBC
∵BD为△ABCB的角平分线
∴∠ABD=∠DBC
∴∠C=∠DBC=∠ABD=30°
∵DA⊥BA,DE⊥BC
∴DE=AD=2
∴CD=2ED=2AD=4
故答案为:D.
分析:根据线段垂直平分线的性质以及角平分线的性质,即可得到DE=AD=2,求出CD的长度即可。
5. C
考点:角平分线的性质
解:∵角平分线上的点到这个角两边的距离相等
∴凉亭的位置应选在△ABC三条角平分线的交点.
故答案为:C.
分析:利用角平分线的性质求解即可。
6. B
考点:三角形全等的判定
解:①作∠BAC的平分线AD交BC于点D,可得 (AAS)则△ABD≌△ACD,即可得AB=AC,故①符合题意;
②取BC边的中点D,连接AD,得BD=CD,AD=AD,∠B=∠C,根据这些条件不能判断△ABD≌△ACD,故②不符合题意;
③过点A作AD⊥BC,垂足为点D,得 (AAS)则△ABD≌△ACD,即可得AB=AC,故③符合题意;
④作BC边的垂直平分线AD,交BC于点D,过已知点不能作出已知线段的垂直平分线,辅助线作法不符合题意,故④不符合题意;
故答案为:B.
分析:根据已知和作辅助线所得的条件,对每一种方法进行分析,看能否判定△ABD≌△ACD即可.
7. C
考点:角平分线的性质
解:①∵∠AOC=∠BOC
∴OC平分∠AOB,即OC为∠AOB的角平分线,正确;
②∵∠AOC=∠AOB
∴∠AOB=2∠AOC=∠AOC+∠BOC
∴∠AOC=∠BOC
∴OC平分∠AOB,即OC为∠AOB的平分线。
③∵∠AOC+∠BOC=∠AOB
∴假设∠AOC=30°,∠BOC=40°,,∠AOB=70°,但是OC不是∠AOB的平分线;④∵∠AOB=2∠BOC=∠AOC+∠BOC
∴∠AOC=∠BOC
∴OC平分∠AOB,即OC为∠AOB的角平分线,正确;
故答案为:C.
分析:根据角平分线的判定和性质,分别进行判断得到答案即可。
8. A
考点:全等三角形的判定与性质
解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N;
∵∠BAD=∠BCD=90°
∴四边形AMCN为矩形,∠MAN=90°;
∵∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
?
∴△ABM≌△ADN(AAS),
∴AM=AN(设为a);△ABM与△ADN的面积相等;
∴四边形ABCD的面积=正方形AMCN的面积;
由勾股定理得:AC2=AM2+MC2 , 而AC=8;
∴2a2=64,a2=32,
故答案为:A.
分析:作辅助线;证明△ABM≌△ADN,得到AM=AN,△ABM与△ADN的面积相等;求出正方形AMCN的面积即可解决问题.
9. C
考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
解:如图, 连接BD、AD,过点D作DF⊥CB于点F.
∵ 的垂直平分线 交 的平分线 于点 ,DE⊥AC,DF⊥BC,
∴BD=AD,DE=DF.∴Rt△AED≌Rt△BFD.
∴BF=AE.
又∵∠ECD=∠FCD,∠CED=∠CFD,CA=CA,∴Rt△CED≌Rt△CFD,
∴CE=CF,
设AE的长度为x,则CE=10-x,CF=CB+BF= CB+AE= 4+x,
∴可列方程10-x=4+x,x=3,∴AE=3;
故答案为:C.
分析:连接BD、AD,过点D作DF⊥CB于点F,利用角平分线及线段垂直平分线的性质可求出BD=AD,DE=DF,依据HL定理可判断出Rt△AED≌Rt△BFD,根据全等三角形的性质即可得出BF=AE,再运用AAS定理可证得Rt△CED≌Rt△CFD,证出CE=CF,设AE的长度为x,根据CE=CF列方程求解即可.
10. A
考点:角平分线的性质
解:过点P作PE⊥BC于E.
∵AB∥CD,PA⊥AB,∴PD⊥CD.
∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE,∴PE=PA=PD.
∵PE=4,∴PA=PD=4,∴AD=PA+PD=8.
故答案为:A.
分析:过点P作PE⊥BC于E,根据角平分线上的点到角的两边的距离相等可得PA=PE,PD=PE,那么PE=PA=PD,又PE=4,进而求出AD的长.
二、填空题
11. 4
考点:全等三角形的判定与性质
解:∵AB∥CF,
∴∠A=∠ACF,
在△AED和△CEF中
,
∴△AED≌△CEF(AAS),
∴FC=AD=5cm,
∴BD=AB-AD=9-5=4(cm).
故答案为:4.
分析:根据二直线平行,内错角相等得出∠A=∠ACF,从而利用AAS判断出△AED≌△CEF,根据全等三角形的对应边相等得出FC=AD=5cm,从而根据BD=AB-AD即可算出答案.
12. 5
考点:角平分线的性质
解:作DE⊥AB于E,
∵BC=20,BD=15,
∴CD=20﹣15=5,
∵∠1=∠2,∠C=90°,DE⊥AB,
∴DE=CD=5.
故答案是:5.
分析:作DE⊥AB于E,根据角平分线上的点到角两边的距离相等即可得出DE=CD=5.
13.
考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
解:如图,连接CD,DB,作DM⊥AB于一点M,
∵AD平分∠A,
∴ ,
在△AFD和△AMD中, ,
∴△AFD≌△AMD(AAS),
∴AF=AM,
∵DE垂直平分线BC,
∴CD=BD(线段垂直平分线上的点到线段两端点距离相等),
∵AD平分∠A,DF⊥AC,DM⊥AB,
∴DF=DM(角平分线上的点到角的两边距离相等)
∵∠AFD=∠DMB=90°,
∴Rt△CDF≌Rt△BDM(HL),
∴BM=CF,
∵ ,
,
又∵ ,
∴ ,
∴ ,
故答案为: .
分析:根据角平分线的性质结合全等三角形的判定定理得出△AFD≌△AMD,即可得出AF=AM,再利用线段垂直平分线的性质得出CD=BD,根据HL得出Rt△CDF≌Rt△BDM,即可得出CF=BM,即可得出答案.
14. 2
考点:角平分线的性质
解:过点P作PD⊥OA于点D,
∵OP平分∠AOB,PB⊥OB,PB=2cm,
∴PD=PB=2cm,
故答案为2.
分析:过点P作PD⊥OA于点D,根据角平分线上的点到角的两边的距离相等可得PD=PB,从而得解.
15. 5:7:6
考点:三角形的面积,角平分线的性质
解:如图,过点P作PD⊥AB于点D,PE⊥BC,PF⊥AC,
∵△ABC的角平分线交于点P,
∴PD=PE=PF.
∵S△ABP= AB PD,S△BCP= BC PE,S△ACP= AC PF,
∴S△ABP∶S△BPC∶S△APC= AB PD: BC PE: AC PF=AB:BC:AC=5:7:6.
分析:如图,过点P作PD⊥AB于点D,PE⊥BC,PF⊥AC,根据角平分线上的点到角两边的距离相等得出PD=PE=PF,根据根据三角形的面积计算方法,由等高三角形的面积之比就等于底之比即可得出答案.
三、解答题
16. (1)证明:∵CE⊥AB,BF⊥AC,
∴∠CEA=90°,∠BFA=90°,
在△ABF和△ACE中, ,
∴△ABF≌△ACE(AAS);
(2)证明:∵△ABF≌△ACE,
∴AF=AE,
又∵AF⊥DF,AE⊥DE,
∴A点在∠EDF的平分线上.
考点:全等三角形的判定与性质
【解析】分析:(1)根据AAS可直接证明△ABF≌△ACE;(2)由△ABF≌△ACE可得AF=AE,结合AF⊥DF,AE⊥DE可得A点在∠EDF的平分线上.
17. (1)30°
(2)解:设∠AOC为x°,则∠BOD为x°,
则∠BOE=x+15,∠BOC=2x+30
∠BOC+∠AOC=180
2x+15+x=180
x=50°,∠AOC=50°
(3)解:α=2β,
理由如下:
∵ ∠COD是直角,∠DOE=β,
∴ ∠COE=∠COD﹣∠DOE=90°﹣β,
∵ OE平分∠BOC ,
∴ ∠BOC=2∠COE=2(90°﹣β),
∵ ∠AOC+∠BOC=180°,
∴ α+2(90°﹣β)=180°,
∴ α=2β
考点:角平分线的性质
【解析】分析:(1)根据∠DOE的度数以及∠COD为直角,即可得到∠COE的度数,根据OE为∠COB的平分线,根据平角的性质得到∠AOC的度数即可;
(2)根据题意,可以设∠AOC=∠BOD为x°,根据角之间的等量关系进行等量代换,根据平角的性质求出∠AOC的度数即可;
(3)根据直角的性质,结合角平分线的性质,即可得到∠BOC的度数,由平角的性质,即可得到α与β的关系。
18. (1)证明:如图1,
∵∠FAD+∠CAE=90°,∠FAD+∠F=90°,
∴∠CAE=∠AFD,
在△ADF和△ECA中, ,
∴△ADF≌△ECA(AAS),
∴AD=CD,FD=AC,
∴CE+CD=AD+CD=AC=FD,即EC+CD=DF;
(2)证明:如图2,
过F点作FD⊥AC交AC于D点,
∵△ADF≌△ECA,
∴FD=AC=BC,
在△FDG和△BCG中, ,
∴△FDG≌△BCG(AAS),
∴GD=CG,
∵ =3
∴
∴ ,
∵AD=CE,AC=BC
∴ ,
∴E点为BC中点;
(3)
考点:全等三角形的判定与性质
解:过F作FD⊥AG的延长线交于点D,如图3,
∵ ,BC=AC,CE=CB+BE,
∴ ,
由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,
∴CG=GD,AD=CE,
∴ ,
∴ .
分析:(1)通过全等三角形△ADF≌△EDA的对应边相等得到:AD=CD,FD=AC,则利用等量代换和图形中相关线段间的和差关系证得结论;(2)过F点作FD⊥AC交AC于D点,根据(1)中结论可得FD=AC=BC,即可证明△FGD≌△BCD,可得DG=CG,根据 =3可证 ,根据AD=CE,AC=BC,即可解题;(3)过F作FD⊥AG的延长线交于点D,易证 ,由(1)(2)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得 的值,即可解题.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
