1.5.1 三角形全等的判定——SSS与三角形的稳定性同步训练(含解析)
文档属性
| 名称 | 1.5.1 三角形全等的判定——SSS与三角形的稳定性同步训练(含解析) | 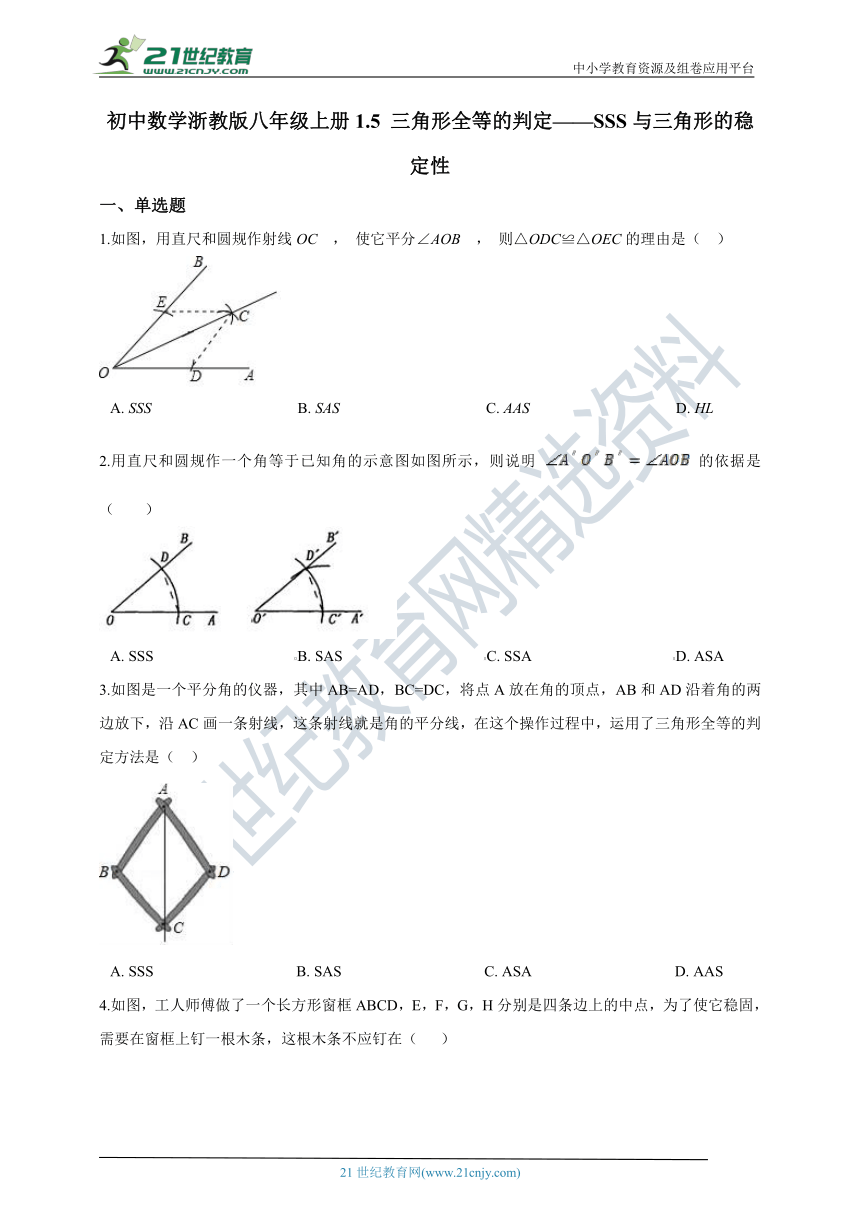 | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 07:16:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册1.5 三角形全等的判定——SSS与三角形的稳定性
一、单选题
1.如图,用直尺和圆规作射线OC , 使它平分∠AOB , 则△ODC≌△OEC的理由是(?? )
A.?SSS??????????????????????????????????????B.?SAS??????????????????????????????????????C.?AAS??????????????????????????????????????D.?HL
2.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明 的依据是(?????? )
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?SSA?????????????????????????????????????D.?ASA
3.如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( ??)
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
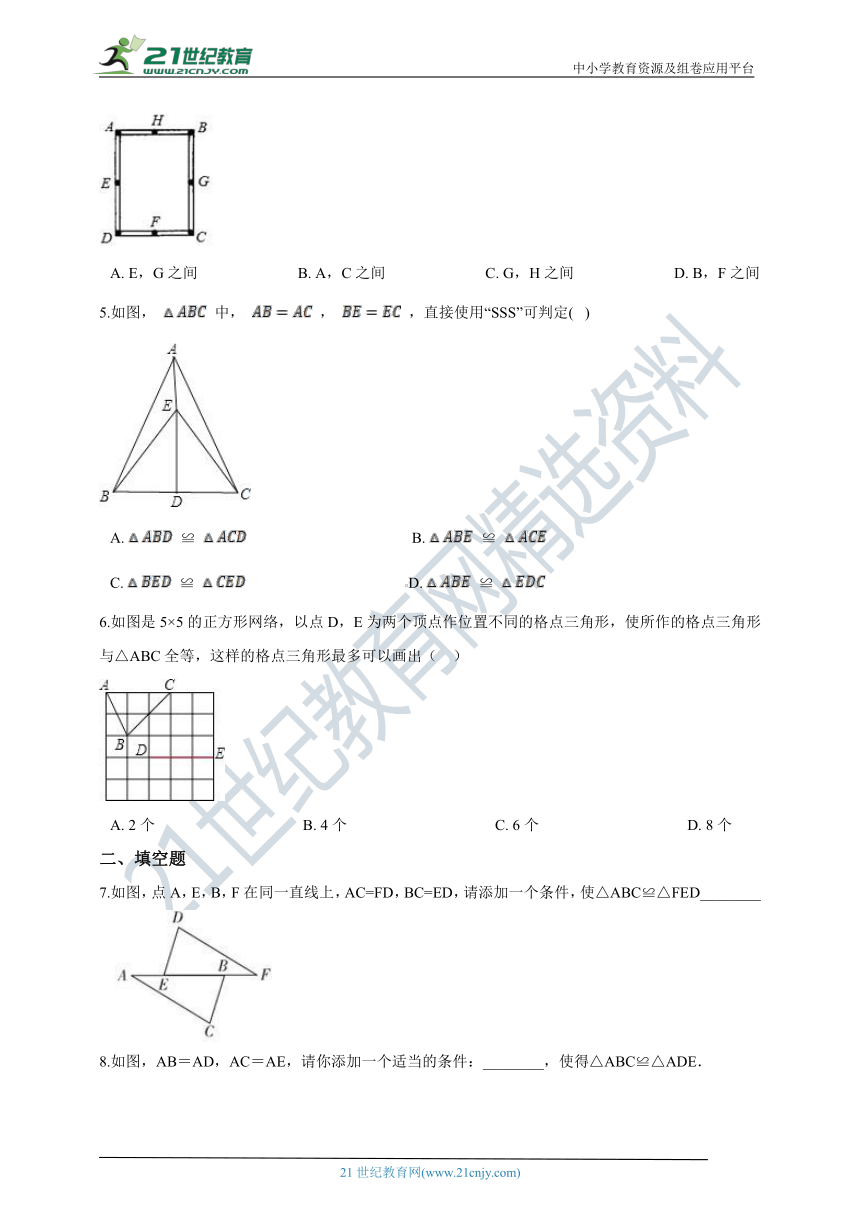
4.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(???? )
A.?E,G之间??????????????????????????B.?A,C之间??????????????????????????C.?G,H之间??????????????????????????D.?B,F之间
5.如图, 中, , ,直接使用“SSS”可判定(? )
A.? ≌ ???????????????????????????????????????????B.? ≌
C.? ≌ ??????????????????????????????????????????D.? ≌
6.如图是5×5的正方形网络,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出(?? )
A.?2个???????????????????????????????????????B.?4个???????????????????????????????????????C.?6个???????????????????????????????????????D.?8个
二、填空题
7.如图,点A,E,B,F在同一直线上,AC=FD,BC=ED,请添加一个条件,使△ABC≌△FED________
8.如图,AB=AD,AC=AE,请你添加一个适当的条件:________,使得△ABC≌△ADE.
9.三角形具有稳定性,要使一个四边形框架稳定不变形,至少需要钉________根木条.
10.如图,小敏做了一个角平分仪ABCD,其中 , ,将仪器上的点A与 的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是 的平分线 此角平分仪的画图原理是:根据仪器结构,可得 ≌ ,这样就有 则说明这两个三角形全等的依据是________
11.如图,AB=AC,BD=CD,若∠B=28°则∠C=________ 度;
三、解答题
12.如图,点A、C、D、B在同一条直线上,且PA=PB,PD=PC,请添加一个条件,使图中△PAD≌△PBC,并给予证明.
(1)你所添加的条件为:________;
(2)写出证明过程.
13.如图,AC=BD,BC=AD,求证:△ABC≌△BAD.
14.已知:如图(没图),A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,求证:△ABC≌△DEF
答案解析部分
一、单选题
1. A
考点:三角形全等的判定
解:由作图可知,OD=OE,DC=EC,
在△ODC与△OEC中
?,
∴△ODC≌△OEC(SSS),
故答案为:A.
分析:根据SSS证明三角形全等即可.
2. A
考点:三角形全等的判定
解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD≌△C'O'D',
故答案为:A.
分析:由作法可知,根据边边边可判断△COD≌△C'O'D'从而求解.
3. A
考点:三角形全等的判定
解:在△ABC和△ADC中,
,
所以△ABC≌△ADC(SSS),
故答案为:A.
分析:根据“SSS”可证△ABC≌△ADC.
4. A
考点:三角形的稳定性
解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
故答案为:A.
分析:根据三角形具有稳定性,只要满足所钉的木条构成三角形即可。
5. B
考点:三角形全等的判定
解:根据AB=AC,BE=EC,AE=AE可以推出△ABE≌△AACE,理由是SSS,
其余△ABD≌△ACD,△BED≌△CED不能直接用SSS定理推出,△ABE和△EDC不全等,
故答案为:B
分析:根据三边对应相等的两个三角形全等可得△ABE≌△AACE。
6. B
考点:三角形全等的判定
解:根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点。
故答案为:B
分析:运用SSS可得与△ABC全等的三角形有4个,画出即可.
二、填空题
7. 答案不唯一,例如AB=EF
考点:三角形全等的判定
解:已知 AC=FD,BC=ED,可根据判定定理SSS进行补充,AB=EF
分析:根据三角形全等的判定定理SSS可进行补充。
8. BC=DE
考点:三角形全等的判定
解:添加条件是:BC=DE,
在△ABC与△ADE中,
,
∴△ABC≌△DEC(SSS).
故答案为:BC=DE(答案不唯一).
分析:本题要判定△ABC≌△ADE,已知AB=AD,AC=AE,具备了两组边对应相等,利用SSS即可判定两三角形全等了
9. 1
考点:三角形的稳定性
解:要使一个四边形框架稳定不变形,至少需要钉1根根木条,使其有两个三角形构成.
故填:1.
分析:根据三角形的稳定性即可求解.
10.SSS
考点:全等三角形的判定与性质
解:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故答案为:SSS
分析:由题意用边边边可证△ADC≌△ABC,根据全等三角形的对应角相等即可求解。
11.28
考点:全等三角形的判定与性质
解:连接线段AD
在△ABD与△ACD中,
∴△ABD≌△ACD
∴∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
分析:由题意构造全等三角形,所以可作辅助线,连接线段AD。由已知条件用边边边可证△ABD≌△ACD,根据全等三角形的性质可得∠B=∠C。
三、解答题
12. (1) (答案不唯一)
(2)解:在△PAD和△PBC中 ∴ .
考点:三角形全等的判定
【解析】分析:(1)根据全等三角形的判定定理填写即可.(2)根据全等三角形的判定定理求证即可.
13. 证明:在△ABC与△BAD中,
,
∴△ABC≌△BAD.
考点:三角形全等的判定
【解析】分析:运用SSS进行证明即可.
14. 证明:∵AF=DC
∴AF-CF=DC-CF
即AC=DF
在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
考点:三角形全等的判定
【解析】分析:先利用等式的性质由已知条件AF=DC得AC=DF,加上已知条件AB=DE,BC=EF,即可利用”SSS“判定△ABC≌△DEF。
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册1.5 三角形全等的判定——SSS与三角形的稳定性
一、单选题
1.如图,用直尺和圆规作射线OC , 使它平分∠AOB , 则△ODC≌△OEC的理由是(?? )
A.?SSS??????????????????????????????????????B.?SAS??????????????????????????????????????C.?AAS??????????????????????????????????????D.?HL
2.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明 的依据是(?????? )
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?SSA?????????????????????????????????????D.?ASA
3.如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( ??)
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
4.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(???? )
A.?E,G之间??????????????????????????B.?A,C之间??????????????????????????C.?G,H之间??????????????????????????D.?B,F之间
5.如图, 中, , ,直接使用“SSS”可判定(? )
A.? ≌ ???????????????????????????????????????????B.? ≌
C.? ≌ ??????????????????????????????????????????D.? ≌
6.如图是5×5的正方形网络,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出(?? )
A.?2个???????????????????????????????????????B.?4个???????????????????????????????????????C.?6个???????????????????????????????????????D.?8个
二、填空题
7.如图,点A,E,B,F在同一直线上,AC=FD,BC=ED,请添加一个条件,使△ABC≌△FED________
8.如图,AB=AD,AC=AE,请你添加一个适当的条件:________,使得△ABC≌△ADE.
9.三角形具有稳定性,要使一个四边形框架稳定不变形,至少需要钉________根木条.
10.如图,小敏做了一个角平分仪ABCD,其中 , ,将仪器上的点A与 的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是 的平分线 此角平分仪的画图原理是:根据仪器结构,可得 ≌ ,这样就有 则说明这两个三角形全等的依据是________
11.如图,AB=AC,BD=CD,若∠B=28°则∠C=________ 度;
三、解答题
12.如图,点A、C、D、B在同一条直线上,且PA=PB,PD=PC,请添加一个条件,使图中△PAD≌△PBC,并给予证明.
(1)你所添加的条件为:________;
(2)写出证明过程.
13.如图,AC=BD,BC=AD,求证:△ABC≌△BAD.
14.已知:如图(没图),A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,求证:△ABC≌△DEF
答案解析部分
一、单选题
1. A
考点:三角形全等的判定
解:由作图可知,OD=OE,DC=EC,
在△ODC与△OEC中
?,
∴△ODC≌△OEC(SSS),
故答案为:A.
分析:根据SSS证明三角形全等即可.
2. A
考点:三角形全等的判定
解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD≌△C'O'D',
故答案为:A.
分析:由作法可知,根据边边边可判断△COD≌△C'O'D'从而求解.
3. A
考点:三角形全等的判定
解:在△ABC和△ADC中,
,
所以△ABC≌△ADC(SSS),
故答案为:A.
分析:根据“SSS”可证△ABC≌△ADC.
4. A
考点:三角形的稳定性
解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
故答案为:A.
分析:根据三角形具有稳定性,只要满足所钉的木条构成三角形即可。
5. B
考点:三角形全等的判定
解:根据AB=AC,BE=EC,AE=AE可以推出△ABE≌△AACE,理由是SSS,
其余△ABD≌△ACD,△BED≌△CED不能直接用SSS定理推出,△ABE和△EDC不全等,
故答案为:B
分析:根据三边对应相等的两个三角形全等可得△ABE≌△AACE。
6. B
考点:三角形全等的判定
解:根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点。
故答案为:B
分析:运用SSS可得与△ABC全等的三角形有4个,画出即可.
二、填空题
7. 答案不唯一,例如AB=EF
考点:三角形全等的判定
解:已知 AC=FD,BC=ED,可根据判定定理SSS进行补充,AB=EF
分析:根据三角形全等的判定定理SSS可进行补充。
8. BC=DE
考点:三角形全等的判定
解:添加条件是:BC=DE,
在△ABC与△ADE中,
,
∴△ABC≌△DEC(SSS).
故答案为:BC=DE(答案不唯一).
分析:本题要判定△ABC≌△ADE,已知AB=AD,AC=AE,具备了两组边对应相等,利用SSS即可判定两三角形全等了
9. 1
考点:三角形的稳定性
解:要使一个四边形框架稳定不变形,至少需要钉1根根木条,使其有两个三角形构成.
故填:1.
分析:根据三角形的稳定性即可求解.
10.SSS
考点:全等三角形的判定与性质
解:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故答案为:SSS
分析:由题意用边边边可证△ADC≌△ABC,根据全等三角形的对应角相等即可求解。
11.28
考点:全等三角形的判定与性质
解:连接线段AD
在△ABD与△ACD中,
∴△ABD≌△ACD
∴∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
分析:由题意构造全等三角形,所以可作辅助线,连接线段AD。由已知条件用边边边可证△ABD≌△ACD,根据全等三角形的性质可得∠B=∠C。
三、解答题
12. (1) (答案不唯一)
(2)解:在△PAD和△PBC中 ∴ .
考点:三角形全等的判定
【解析】分析:(1)根据全等三角形的判定定理填写即可.(2)根据全等三角形的判定定理求证即可.
13. 证明:在△ABC与△BAD中,
,
∴△ABC≌△BAD.
考点:三角形全等的判定
【解析】分析:运用SSS进行证明即可.
14. 证明:∵AF=DC
∴AF-CF=DC-CF
即AC=DF
在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
考点:三角形全等的判定
【解析】分析:先利用等式的性质由已知条件AF=DC得AC=DF,加上已知条件AB=DE,BC=EF,即可利用”SSS“判定△ABC≌△DEF。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
