1.5.2 三角形全等的判定——SAS和线段垂直平分线同步训练(含解析)
文档属性
| 名称 | 1.5.2 三角形全等的判定——SAS和线段垂直平分线同步训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-23 07:18:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册1.5 三角形全等的判定——SAS和线段垂直平分线
一、单选题
1.如图,将两根钢条AA?,BB?的中点连接在一起,使AA?,BB?可以绕着点O自由转动,就做成了一个测量工具(卡钳),则图中AB的长等于内槽宽A?B?,那么判定△OAB≌△O A?B?的理由是(?? ?)
A.?边角边????????????????????????????????B.?边边边????????????????????????????????C.?角边角????????????????????????????????D.?角角边
2.如图,在△ABC中,AB的垂直平分线交AC于点D, 交AB于点E , 如果 ?cm,? ?cm,那么△ 的周长是(?????? )
A.?6 cm???????????????????????????????????B.?7 cm???????????????????????????????????C.?8 cm???????????????????????????????????D.?9 cm
3.如图,已知△ABC的三条角平分线交于点O,且∠BAC=120°,延长CA至点D,使DC=BC,连接OD,则∠BOD的度数为(??? )
A.?45°???????????????????????????????????????B.?50°???????????????????????????????????????C.?60°???????????????????????????????????????D.?75°
4.如图,在△ABC中,DE是边AC的垂直平分线,且分别交BC,AC干点D,E,连接AD,若∠B=70°,∠BAD=60°,则∠C为(??? )
A.?20°???????????????????????????????????????B.?25°???????????????????????????????????????C.?30°???????????????????????????????????????D.?50°
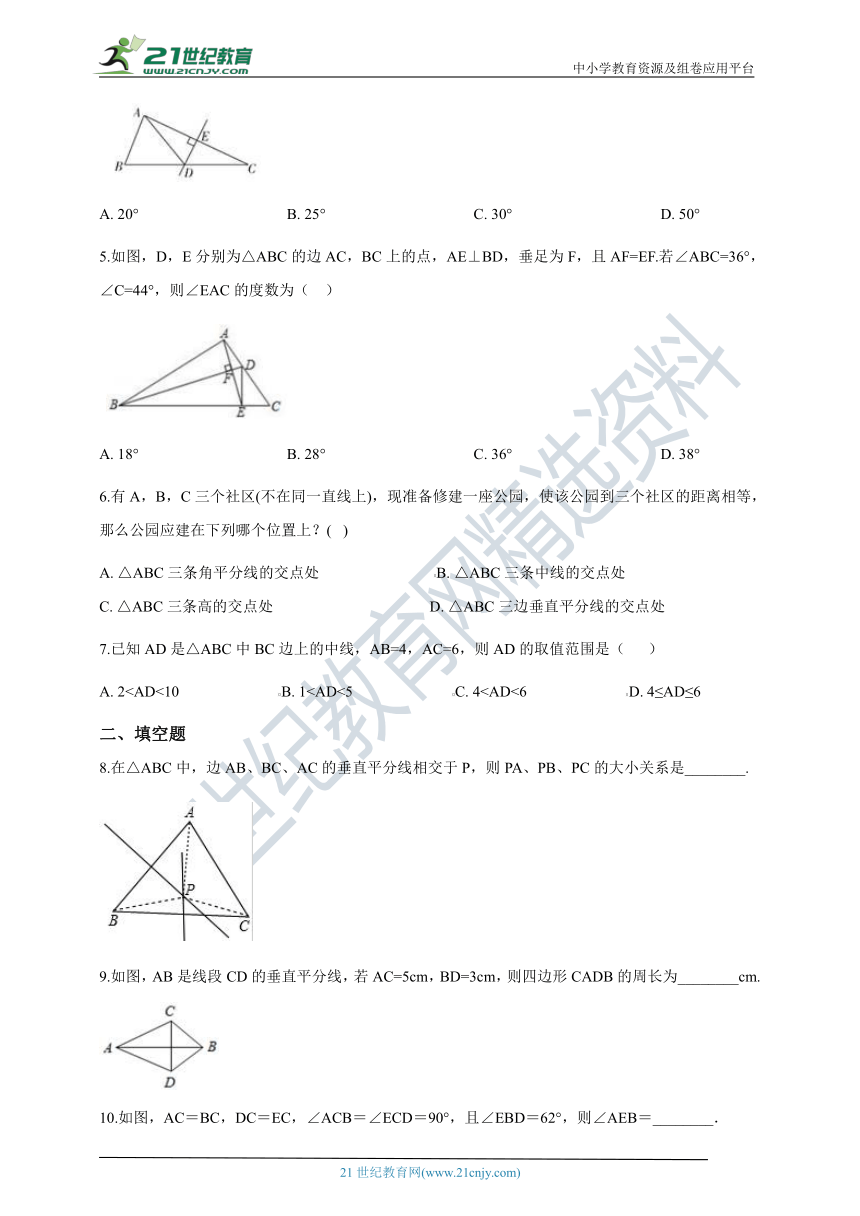
5.如图,D,E分别为△ABC的边AC,BC上的点,AE⊥BD,垂足为F,且AF=EF.若∠ABC=36°,∠C=44°,则∠EAC的度数为(?? )
A.?18°???????????????????????????????????????B.?28°???????????????????????????????????????C.?36°???????????????????????????????????????D.?38°
6.有A,B,C三个社区(不在同一直线上),现准备修建一座公园,使该公园到三个社区的距离相等,那么公园应建在下列哪个位置上?(? )
A.?△ABC三条角平分线的交点处??????????????????????????????B.?△ABC三条中线的交点处
C.?△ABC三条高的交点处?????????????????????????????????????????D.?△ABC三边垂直平分线的交点处
7.已知AD是△ABC中BC边上的中线,AB=4,AC=6,则AD的取值范围是(???? )
A.?2二、填空题
8.在△ABC中,边AB、BC、AC的垂直平分线相交于P,则PA、PB、PC的大小关系是________.
9.如图,AB是线段CD的垂直平分线,若AC=5cm,BD=3cm,则四边形CADB的周长为________cm.
10.如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=62°,则∠AEB=________.
11.在△ 中, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧分别交于点 ,作直线 交 于点 ,则 的度数是 ________.
12.如图,∠BAC=∠ABD,请你添加一个条件:________,能使△ABD≌△BAC(只添一个即可).
13.如图所示, , , ,点 在线段 上,若 , ,则 ________ .
三、解答题
14.如图,有一个池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接达到点 和 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长度就是 , 的距离,为什么?
15.如图,AB=AC,AD=AE,∠BAD=∠CAE,求证:BE=CD。
16.综合与实践
智慧小组将两个三角形纸片(△OAB和△OCD)按如图1摆放,其中∠AOB=∠COD,∠OAB=∠OBA,OA=OB,OC=OD。连接AC,BD,交点为M。
(1)请直接写出AC与BD存在的数量关系:
(2)将△OAB保持固定不动,△OCD绕点O转动到图2位置,猜想此时(1) 中结论还成立吗?请说明理由;
(3)智慧小组测量发现图1中∠AMB=∠AOB,由此组长大胆猜想:图2中∠AMB的大小也等于∠AOB。如果你是智慧小组的一员,你赞成组长的猜想吗?请说明理由。
答案解析部分
一、单选题
1. A
考点:三角形全等的判定
解:∵O是 的中点,
∴ , , ,
在 和 中,
,
∴ ?(SAS),
所以理由是:边角边.
故答案为:A.
分析:已知两边和夹角相等,利用SAS可证两个三角形全等.
2. D
考点:线段垂直平分线的性质
解:∵AC是AB的垂直平分线
∴AD=BD
∴CD+BD=CD+AD=AC=5
∴△DBC的周长为:CD+BD+BC=AC+BC=5+4=9(cm).
故答案为:D.
分析:先利用线段的垂直平分线的性质得AD=BD,则CD+BD=CD+AD=AC=5,进而可求出△DBC的周长。
3. C
考点:全等三角形的判定与性质
解:根据题意可知,∠DCO=∠BCO,通过SAS定理,
可判断出△OCD≌△OCB,
所以∠D=∠OBC=∠ABO
∠BOD=∠ABC+∠ACB=180°-∠BAC=60°
故答案为:C
分析:根据全等三角形的判定和性质,进行计算即可。
4. B
考点:线段垂直平分线的性质
解:∠ADB=180°-70°-60°=50°,所以∠ADC=180°-50°=130°,
∠EDC=65°,∠C=180°-65°-90°=25°
故答案为:B
分析:根据垂直平分线的性质,进行角度换算即可。
5. B
考点:线段垂直平分线的性质
解:?∵ AE⊥BD , AF=EF
? ?∴?BD是AE垂直平分线
? ?∴?BAE=BEA?
? ?∵? ∠ABC=36°,∠C=44°
? ?∴??BAE=BEA?=(180°- ∠ABC)2=(180°- 36°)2=72°
? ? ?EAC=BAE-∠C=72°-44°=28°
? ? ?故答案为:B.
分析:由AE⊥BD , AF=EF?得出BD是AE垂直平分线,利用垂直平分线的性质得到BAE=BEA ,利用三角形内角和是180°和∠ABC=36°求出在ABE中,BAE=BEA?=72°,利用三角形的外角等于和它不相邻的两个内角和以及∠C=44° 得出在AEC中,EAC=BAE-∠C=28°? 即可以得到结果。
6. D
考点:线段垂直平分线的性质
解:∵根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等。则超市应建在△ABC三条边的垂直平分线的交点处。
分析:要求到三小区的距离相等,首先想到A小区、B小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上,同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上,于是到三个小区的距离相等的点应是其交点,又因为三角形三边的垂直平分线相交于一点,可得结果.
7. B
考点:全等三角形的判定与性质
解:如图,延长AD到点E,使DE=AD,
∵AD是△ABC中BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵AB=4,AC=6,
∴6-4 即2 ∴1 故答案为:B.
分析:延长AD到点E,使DE=AD,利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得CE=AB,再根据三角形两边之和大于第三边,两边之差小于第三边求出AE的取值范围,然后即可得解. 关键是作出辅助线构造出合适的全等三角形,遇中点,常见辅助线是“倍长中线”.
二、填空题
8. PA=PB=PC
考点:线段垂直平分线的性质
解:∵边AB的垂直平分线相交于P,
∴PA=PB,
∵边BC的垂直平分线相交于P,
∴PB=PC,
∴PA=PB=PC.
故答案为:PA=PB=PC.
分析:根据线段垂直平分线上的点,到线段两个端点的距离相等得出PA=PB,PB=PC,进而根据等量代换即可得出结论.
9. 16
考点:线段垂直平分线的性质
解:∵AB是线段CD的垂直平分线,AC=5cm,BD=3cm
∴
∴四边形CADB的周长
故答案为:16.
分析:根据垂直平分线的性质可得 ,即可求出四边形CADB的周长.
10. 152°
考点:三角形内角和定理,全等三角形的判定与性质
解:∵∠ACB=∠ECD=90°,
∴∠ACB?∠BCE=∠ECD?∠BCE,即∠ACE=∠BCD,
在△ACE和△BCD中, ,
∴△ACE≌△BCD,
∴∠CAE=∠CBD,
∴∠CAE+∠CBE=∠CBD+∠CBE=∠EBD=62°,
在△ABC中,∠EAB+∠EBA=180°?(∠ACB+∠CAE+∠CBE)=180°?(90°+62°)=28°,
在△ABE中,∠AEB=180°?(∠EAB+∠EBA)=180°?28°=152°,
故答案为:152°.
分析:先求出∠ACE=∠BCD,再利用“边角边”证明△ACE和△BCD全等,根据全等三角形对应角相等可得∠CAE=∠CBD,从而求出∠CAE+∠CBE=∠EBD,再利用三角形的内角和等于180°列式求出∠EAB+∠EBA,然后再次利用三角形的内角和等于180°列式计算即可得解.
11. 20°
考点:三角形内角和定理,线段垂直平分线的性质
解:∵∠C=80°,∠A=40°,
∴∠ABC=180°-∠A-∠C=60°
由作图可知,EF为线段AB的垂直平分线,
∴AD=BD,
∴∠DBA=∠A=40°,
∴∠CBD=∠ABC-∠ABD=60°-40°=20°.
故答案为:20°.
分析:先根据三角形内角和定理求出∠ABC=60°,再根据线段垂直平分线的性质得出∠ABD=40°,进而可得出∠CBD的度数.
12. BD=AC
考点:三角形全等的判定
解:∠BAC=∠ABD(已知),AB=BA(公共边),BD=AC,
∴△DAB≌△CBA(SAS);
故答案为BD=AC.本题答案不唯一.
分析:本题要判定△ABD≌△BAC,已知AB是公共边,∠BAC=∠ABD具备了一组边、一对角对应相等,故添加AC=BD后可以根据SAS判定△ABD≌△BAC.
13. 55°
考点:三角形的外角性质,全等三角形的判定与性质
解:在△ABD与△ACE中,
∵∠1+∠CAD=∠CAE+∠CAD,
∴∠1=∠CAE;
∴△ABD≌△ACE(SAS);
∴∠2=∠ABE=30°;
∵∠3=∠1+∠ABE,∠1=25°,
∴∠3=55°.
故答案为:55°.
分析:根据已知先证明△ABD≌△ACE(SAS);再利用全等三角形的性质,求得∠2=∠ABE;最后根据三角形外角的性质即可求出答案.
三、解答题
14. 证明:在 和 中,
考点:全等三角形的判定与性质
【解析】分析:利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答.
15. 证明:∵∠BAD=∠CAE
∴∠BAD+∠DAE=∠CAE+∠DAE即∠BAE=∠CAD
在△ABE和△CAD中
∴△ABE≌△CAD(SAS)
∴BE=CD.
考点:全等三角形的判定与性质
分析:由已知∠BAD=∠CAE可以推出∠BAE=∠CAD,再利用SAS证明△ABE≌△CAD,然后利用全等三角形的对应边相等,可证得结论。
16. (1)AC=BD
(2)(1)中的结论仍然成立,理由如下:
∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS) ,
∴AC=BD
(3)赞成,理由如下:
由(2) 得△AOC≌△BOD,
∴∠OAC=∠OBD,
又∵∠OAB=∠OBA,
∴∠OAB+∠OBA=∠OAC+∠CAB+∠OBA=∠OBD+∠CAB+∠OBA=∠ABM+∠MAB,
在△AMB中,∠AMB=180°-(∠ABM+∠MAB) ,
在△OAB中,∠AOB=180°-(∠OAB+∠OBA)
∴∠AMB=∠AOB
考点:全等三角形的判定与性质
分析:(1)根据题意,可直接写出关系。
(2)根据三角形全等的判定定理SAS,可证明其全等,根据全等三角形的性质求出即可。
(3)根据三角形全等的性质,利用角度换算,可得出结论。
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册1.5 三角形全等的判定——SAS和线段垂直平分线
一、单选题
1.如图,将两根钢条AA?,BB?的中点连接在一起,使AA?,BB?可以绕着点O自由转动,就做成了一个测量工具(卡钳),则图中AB的长等于内槽宽A?B?,那么判定△OAB≌△O A?B?的理由是(?? ?)
A.?边角边????????????????????????????????B.?边边边????????????????????????????????C.?角边角????????????????????????????????D.?角角边
2.如图,在△ABC中,AB的垂直平分线交AC于点D, 交AB于点E , 如果 ?cm,? ?cm,那么△ 的周长是(?????? )
A.?6 cm???????????????????????????????????B.?7 cm???????????????????????????????????C.?8 cm???????????????????????????????????D.?9 cm
3.如图,已知△ABC的三条角平分线交于点O,且∠BAC=120°,延长CA至点D,使DC=BC,连接OD,则∠BOD的度数为(??? )
A.?45°???????????????????????????????????????B.?50°???????????????????????????????????????C.?60°???????????????????????????????????????D.?75°
4.如图,在△ABC中,DE是边AC的垂直平分线,且分别交BC,AC干点D,E,连接AD,若∠B=70°,∠BAD=60°,则∠C为(??? )
A.?20°???????????????????????????????????????B.?25°???????????????????????????????????????C.?30°???????????????????????????????????????D.?50°
5.如图,D,E分别为△ABC的边AC,BC上的点,AE⊥BD,垂足为F,且AF=EF.若∠ABC=36°,∠C=44°,则∠EAC的度数为(?? )
A.?18°???????????????????????????????????????B.?28°???????????????????????????????????????C.?36°???????????????????????????????????????D.?38°
6.有A,B,C三个社区(不在同一直线上),现准备修建一座公园,使该公园到三个社区的距离相等,那么公园应建在下列哪个位置上?(? )
A.?△ABC三条角平分线的交点处??????????????????????????????B.?△ABC三条中线的交点处
C.?△ABC三条高的交点处?????????????????????????????????????????D.?△ABC三边垂直平分线的交点处
7.已知AD是△ABC中BC边上的中线,AB=4,AC=6,则AD的取值范围是(???? )
A.?2
8.在△ABC中,边AB、BC、AC的垂直平分线相交于P,则PA、PB、PC的大小关系是________.
9.如图,AB是线段CD的垂直平分线,若AC=5cm,BD=3cm,则四边形CADB的周长为________cm.
10.如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=62°,则∠AEB=________.
11.在△ 中, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧分别交于点 ,作直线 交 于点 ,则 的度数是 ________.
12.如图,∠BAC=∠ABD,请你添加一个条件:________,能使△ABD≌△BAC(只添一个即可).
13.如图所示, , , ,点 在线段 上,若 , ,则 ________ .
三、解答题
14.如图,有一个池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接达到点 和 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长度就是 , 的距离,为什么?
15.如图,AB=AC,AD=AE,∠BAD=∠CAE,求证:BE=CD。
16.综合与实践
智慧小组将两个三角形纸片(△OAB和△OCD)按如图1摆放,其中∠AOB=∠COD,∠OAB=∠OBA,OA=OB,OC=OD。连接AC,BD,交点为M。
(1)请直接写出AC与BD存在的数量关系:
(2)将△OAB保持固定不动,△OCD绕点O转动到图2位置,猜想此时(1) 中结论还成立吗?请说明理由;
(3)智慧小组测量发现图1中∠AMB=∠AOB,由此组长大胆猜想:图2中∠AMB的大小也等于∠AOB。如果你是智慧小组的一员,你赞成组长的猜想吗?请说明理由。
答案解析部分
一、单选题
1. A
考点:三角形全等的判定
解:∵O是 的中点,
∴ , , ,
在 和 中,
,
∴ ?(SAS),
所以理由是:边角边.
故答案为:A.
分析:已知两边和夹角相等,利用SAS可证两个三角形全等.
2. D
考点:线段垂直平分线的性质
解:∵AC是AB的垂直平分线
∴AD=BD
∴CD+BD=CD+AD=AC=5
∴△DBC的周长为:CD+BD+BC=AC+BC=5+4=9(cm).
故答案为:D.
分析:先利用线段的垂直平分线的性质得AD=BD,则CD+BD=CD+AD=AC=5,进而可求出△DBC的周长。
3. C
考点:全等三角形的判定与性质
解:根据题意可知,∠DCO=∠BCO,通过SAS定理,
可判断出△OCD≌△OCB,
所以∠D=∠OBC=∠ABO
∠BOD=∠ABC+∠ACB=180°-∠BAC=60°
故答案为:C
分析:根据全等三角形的判定和性质,进行计算即可。
4. B
考点:线段垂直平分线的性质
解:∠ADB=180°-70°-60°=50°,所以∠ADC=180°-50°=130°,
∠EDC=65°,∠C=180°-65°-90°=25°
故答案为:B
分析:根据垂直平分线的性质,进行角度换算即可。
5. B
考点:线段垂直平分线的性质
解:?∵ AE⊥BD , AF=EF
? ?∴?BD是AE垂直平分线
? ?∴?BAE=BEA?
? ?∵? ∠ABC=36°,∠C=44°
? ?∴??BAE=BEA?=(180°- ∠ABC)2=(180°- 36°)2=72°
? ? ?EAC=BAE-∠C=72°-44°=28°
? ? ?故答案为:B.
分析:由AE⊥BD , AF=EF?得出BD是AE垂直平分线,利用垂直平分线的性质得到BAE=BEA ,利用三角形内角和是180°和∠ABC=36°求出在ABE中,BAE=BEA?=72°,利用三角形的外角等于和它不相邻的两个内角和以及∠C=44° 得出在AEC中,EAC=BAE-∠C=28°? 即可以得到结果。
6. D
考点:线段垂直平分线的性质
解:∵根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等。则超市应建在△ABC三条边的垂直平分线的交点处。
分析:要求到三小区的距离相等,首先想到A小区、B小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上,同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上,于是到三个小区的距离相等的点应是其交点,又因为三角形三边的垂直平分线相交于一点,可得结果.
7. B
考点:全等三角形的判定与性质
解:如图,延长AD到点E,使DE=AD,
∵AD是△ABC中BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵AB=4,AC=6,
∴6-4
分析:延长AD到点E,使DE=AD,利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得CE=AB,再根据三角形两边之和大于第三边,两边之差小于第三边求出AE的取值范围,然后即可得解. 关键是作出辅助线构造出合适的全等三角形,遇中点,常见辅助线是“倍长中线”.
二、填空题
8. PA=PB=PC
考点:线段垂直平分线的性质
解:∵边AB的垂直平分线相交于P,
∴PA=PB,
∵边BC的垂直平分线相交于P,
∴PB=PC,
∴PA=PB=PC.
故答案为:PA=PB=PC.
分析:根据线段垂直平分线上的点,到线段两个端点的距离相等得出PA=PB,PB=PC,进而根据等量代换即可得出结论.
9. 16
考点:线段垂直平分线的性质
解:∵AB是线段CD的垂直平分线,AC=5cm,BD=3cm
∴
∴四边形CADB的周长
故答案为:16.
分析:根据垂直平分线的性质可得 ,即可求出四边形CADB的周长.
10. 152°
考点:三角形内角和定理,全等三角形的判定与性质
解:∵∠ACB=∠ECD=90°,
∴∠ACB?∠BCE=∠ECD?∠BCE,即∠ACE=∠BCD,
在△ACE和△BCD中, ,
∴△ACE≌△BCD,
∴∠CAE=∠CBD,
∴∠CAE+∠CBE=∠CBD+∠CBE=∠EBD=62°,
在△ABC中,∠EAB+∠EBA=180°?(∠ACB+∠CAE+∠CBE)=180°?(90°+62°)=28°,
在△ABE中,∠AEB=180°?(∠EAB+∠EBA)=180°?28°=152°,
故答案为:152°.
分析:先求出∠ACE=∠BCD,再利用“边角边”证明△ACE和△BCD全等,根据全等三角形对应角相等可得∠CAE=∠CBD,从而求出∠CAE+∠CBE=∠EBD,再利用三角形的内角和等于180°列式求出∠EAB+∠EBA,然后再次利用三角形的内角和等于180°列式计算即可得解.
11. 20°
考点:三角形内角和定理,线段垂直平分线的性质
解:∵∠C=80°,∠A=40°,
∴∠ABC=180°-∠A-∠C=60°
由作图可知,EF为线段AB的垂直平分线,
∴AD=BD,
∴∠DBA=∠A=40°,
∴∠CBD=∠ABC-∠ABD=60°-40°=20°.
故答案为:20°.
分析:先根据三角形内角和定理求出∠ABC=60°,再根据线段垂直平分线的性质得出∠ABD=40°,进而可得出∠CBD的度数.
12. BD=AC
考点:三角形全等的判定
解:∠BAC=∠ABD(已知),AB=BA(公共边),BD=AC,
∴△DAB≌△CBA(SAS);
故答案为BD=AC.本题答案不唯一.
分析:本题要判定△ABD≌△BAC,已知AB是公共边,∠BAC=∠ABD具备了一组边、一对角对应相等,故添加AC=BD后可以根据SAS判定△ABD≌△BAC.
13. 55°
考点:三角形的外角性质,全等三角形的判定与性质
解:在△ABD与△ACE中,
∵∠1+∠CAD=∠CAE+∠CAD,
∴∠1=∠CAE;
∴△ABD≌△ACE(SAS);
∴∠2=∠ABE=30°;
∵∠3=∠1+∠ABE,∠1=25°,
∴∠3=55°.
故答案为:55°.
分析:根据已知先证明△ABD≌△ACE(SAS);再利用全等三角形的性质,求得∠2=∠ABE;最后根据三角形外角的性质即可求出答案.
三、解答题
14. 证明:在 和 中,
考点:全等三角形的判定与性质
【解析】分析:利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答.
15. 证明:∵∠BAD=∠CAE
∴∠BAD+∠DAE=∠CAE+∠DAE即∠BAE=∠CAD
在△ABE和△CAD中
∴△ABE≌△CAD(SAS)
∴BE=CD.
考点:全等三角形的判定与性质
分析:由已知∠BAD=∠CAE可以推出∠BAE=∠CAD,再利用SAS证明△ABE≌△CAD,然后利用全等三角形的对应边相等,可证得结论。
16. (1)AC=BD
(2)(1)中的结论仍然成立,理由如下:
∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS) ,
∴AC=BD
(3)赞成,理由如下:
由(2) 得△AOC≌△BOD,
∴∠OAC=∠OBD,
又∵∠OAB=∠OBA,
∴∠OAB+∠OBA=∠OAC+∠CAB+∠OBA=∠OBD+∠CAB+∠OBA=∠ABM+∠MAB,
在△AMB中,∠AMB=180°-(∠ABM+∠MAB) ,
在△OAB中,∠AOB=180°-(∠OAB+∠OBA)
∴∠AMB=∠AOB
考点:全等三角形的判定与性质
分析:(1)根据题意,可直接写出关系。
(2)根据三角形全等的判定定理SAS,可证明其全等,根据全等三角形的性质求出即可。
(3)根据三角形全等的性质,利用角度换算,可得出结论。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
