浙教版数学八年级上册第一章三角形的认识学案(pdf版)
文档属性
| 名称 | 浙教版数学八年级上册第一章三角形的认识学案(pdf版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 07:14:22 | ||
图片预览


文档简介
教n年袋上
三鼎和认识
理人:余
第一章三角形的初步认识
重难点学习手册
教n年袋上
三鼎和认识
理人:余
晰教版A年袋上
三鼎和认识
理人:余
第一章三角形的初步认识
1.1认识三角形1.2定义与命题13证明
14全等三角形1.5全等三角形的判定1.6尺规作图
模块一:知识点精析篇
11认识三角形12定义与命题
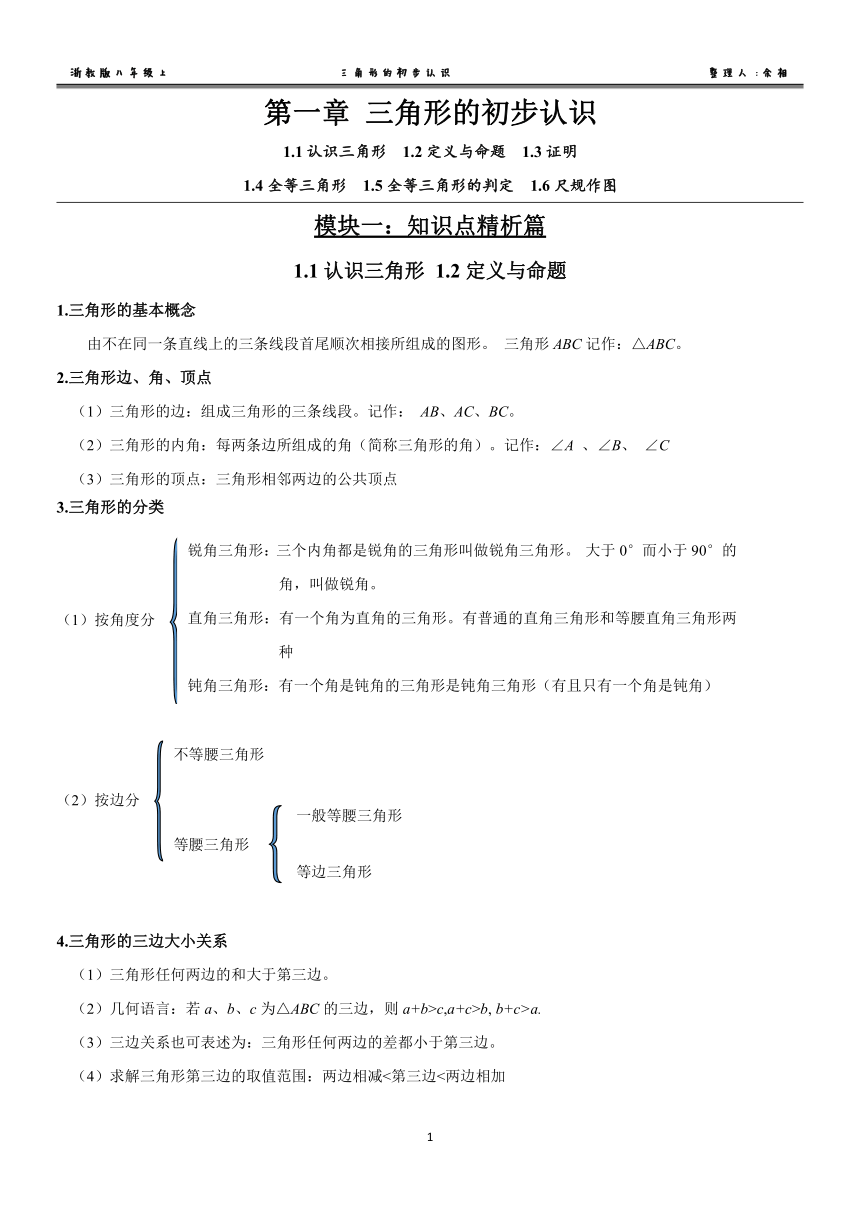
1.三角形的基本概念
由不在同一条直线上的三条线段首尾顺次相接所组成的图形。三角形ABC记作:△ABC。
2三角形边、角、顶点
(1)三角形的边:组成三角形的三条线段。记作:AB、AC、BC。
(2)三角形的内角:每两条边所组成的角(简称三角形的角)。记作:∠A、∠B、∠C
(3)三角形的顶点:三角形相邻两边的公共顶点
3.三角形的分类
锐角三角形:三个内角都是锐角的三角形叫做锐角三角形。大于0°而小于90°的
角,叫做锐角
(1)按角度分《直角三角形;有一个角为直角的三角形。有普通的直角三角形和等腰直角三角形两
钝角三角形:有一个角是钝角的三角形是钝角三角形(有且只有一个角是钝角)
不等腰三角形
(2)按边分
一般等腰三角形
等腰三角形
等边三角形
4.三角形的三边大小关系
(1)三角形任何两边的和大于第三边
(2)几何语言:若a、b、c为△ABC的三边,则a+b>c,a+c>b,b+c>a
(3)三边关系也可表述为:三角形任何两边的差都小于第三边。
(4)求解三角形第三边的取值范围:两边相减<第三边<两边相加
浙教版A年级上
三鼎和认识
理人:余
5判断三条线段能否构成三角形的方法:
①先找出最长的线段,
②然后计算较短的两条线段的和
③如果小于等于最长线段,不能构成三角形。如果大于最长线段能构成三角形
6.三角形周长与最长边的关系
设三角形周长为A,三角形最长边为x则x的取值范围是≤x<4
推导:三角形最长边为x,其余两边之和ax根据
a-xx,
a-x-xsx共同解出即得到2sx<4
7三角形的内角和定理
(1)三角形三个内角的和等于180。
(2)几何语言:△ABC中,∠A+∠B+∠C=1800。
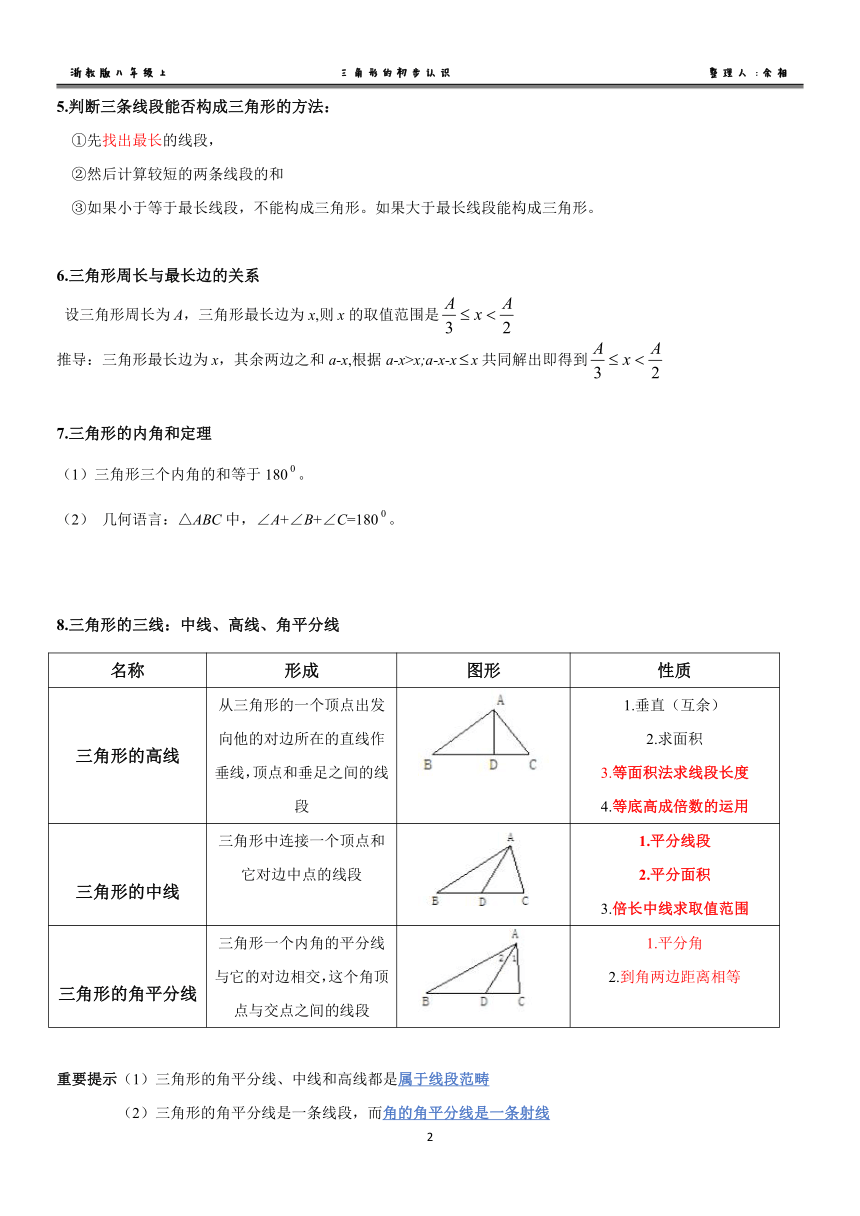
8三角形的三线:中线、高线、角平分线
名称
形成
图形
性质
从三角形的一个顶点出发
1.垂直(互余)
向他的对边所在的直线作
2求面积
三角形的高线
垂线,顶点和垂足之间的线B
3等面积法求线段长度
段
4等底高成倍数的运用
三角形中连接一个顶点和
1.平分线段
它对边中点的线段
2平分面积
三角形的中线
3倍长中线求取值范围
角形一个内角的平分线
1.平分角
与它的对边相交,这个角顶
2.到角两边距离相等
角形的角平分线
点与交点之间的线段
重要提示(1)三角形的角平分线、中线和高线都是属于线段范畴
(2)三角形的角平分线是一条线段,而角的角平分线是一条射线
三鼎和认识
理人:余
第一章三角形的初步认识
重难点学习手册
教n年袋上
三鼎和认识
理人:余
晰教版A年袋上
三鼎和认识
理人:余
第一章三角形的初步认识
1.1认识三角形1.2定义与命题13证明
14全等三角形1.5全等三角形的判定1.6尺规作图
模块一:知识点精析篇
11认识三角形12定义与命题
1.三角形的基本概念
由不在同一条直线上的三条线段首尾顺次相接所组成的图形。三角形ABC记作:△ABC。
2三角形边、角、顶点
(1)三角形的边:组成三角形的三条线段。记作:AB、AC、BC。
(2)三角形的内角:每两条边所组成的角(简称三角形的角)。记作:∠A、∠B、∠C
(3)三角形的顶点:三角形相邻两边的公共顶点
3.三角形的分类
锐角三角形:三个内角都是锐角的三角形叫做锐角三角形。大于0°而小于90°的
角,叫做锐角
(1)按角度分《直角三角形;有一个角为直角的三角形。有普通的直角三角形和等腰直角三角形两
钝角三角形:有一个角是钝角的三角形是钝角三角形(有且只有一个角是钝角)
不等腰三角形
(2)按边分
一般等腰三角形
等腰三角形
等边三角形
4.三角形的三边大小关系
(1)三角形任何两边的和大于第三边
(2)几何语言:若a、b、c为△ABC的三边,则a+b>c,a+c>b,b+c>a
(3)三边关系也可表述为:三角形任何两边的差都小于第三边。
(4)求解三角形第三边的取值范围:两边相减<第三边<两边相加
浙教版A年级上
三鼎和认识
理人:余
5判断三条线段能否构成三角形的方法:
①先找出最长的线段,
②然后计算较短的两条线段的和
③如果小于等于最长线段,不能构成三角形。如果大于最长线段能构成三角形
6.三角形周长与最长边的关系
设三角形周长为A,三角形最长边为x则x的取值范围是≤x<4
推导:三角形最长边为x,其余两边之和ax根据
a-xx,
a-x-xsx共同解出即得到2sx<4
7三角形的内角和定理
(1)三角形三个内角的和等于180。
(2)几何语言:△ABC中,∠A+∠B+∠C=1800。
8三角形的三线:中线、高线、角平分线
名称
形成
图形
性质
从三角形的一个顶点出发
1.垂直(互余)
向他的对边所在的直线作
2求面积
三角形的高线
垂线,顶点和垂足之间的线B
3等面积法求线段长度
段
4等底高成倍数的运用
三角形中连接一个顶点和
1.平分线段
它对边中点的线段
2平分面积
三角形的中线
3倍长中线求取值范围
角形一个内角的平分线
1.平分角
与它的对边相交,这个角顶
2.到角两边距离相等
角形的角平分线
点与交点之间的线段
重要提示(1)三角形的角平分线、中线和高线都是属于线段范畴
(2)三角形的角平分线是一条线段,而角的角平分线是一条射线
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
