2.6 直角三角形(1)课件(共15张PPT)
文档属性
| 名称 | 2.6 直角三角形(1)课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-24 21:54:53 | ||
图片预览






文档简介
(共15张PPT)
直角三角形
浙教版
八年级
新知导入
斜边
直角边
两个图中的△ABC具有怎样的共同特点?它们是什么特殊的三角形?
有一个角是直角的三角形叫直角三角形.
直角三角形用符号“Rt△“表示,如上图中的直角三角形△ABC记作:
Rt△ABC
新知讲解
拓展延伸
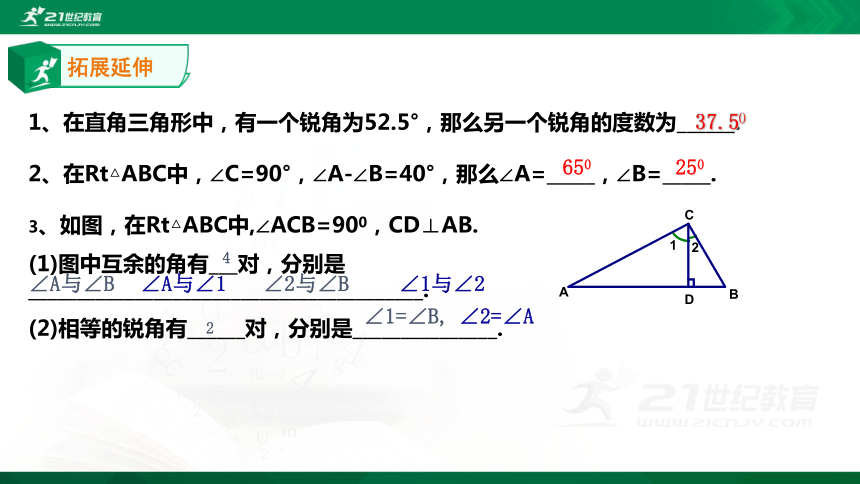
1、在直角三角形中,有一个锐角为52.5°,那么另一个锐角的度数为______.
2、在Rt△ABC中,∠C=90°,∠A-∠B=40°,那么∠A=_____,∠B=_____.
37.50
650
250
3、如图,在Rt△ABC中,∠ACB=900,CD⊥AB.
(1)图中互余的角有___对,分别是_________________________________________.
(2)相等的锐角有______对,分别是_______________.
4
∠A与∠B
∠A与∠1
∠2与∠B
∠1与∠2
2
∠1=∠B,
∠2=∠A
新知讲解
如图,已知Rt△ABC,画一条线段把Rt△ABC分成两个等腰三角形.
小明说:当∠A=450时我会画,我的画法是:过点C画直线CD,交AB于D,使∠ACD=∠
A=450,则线段CD即为所求.
小亮说:当∠A=300时我也会画,我的画法是:过点C画直线CD,交AB于D,使∠ACD=∠
A=
300,则线段CD即为所求.
当∠A的度数任意时,你能画出这条线段吗?若能,说说你的画法.
图中你能证明△DCB是等腰三角形吗?图中的线段CD是直角三角形的什么线?
CD与AB有什么数量关系?由此你有什么发现?
新知讲解
直角三角形的性质定理2:
直角三角形斜边上的中线等于斜边的一半.
几何语言:
新知讲解
直角三角形的性质定理3:
在直角三角形中,如果一个锐角等于300,那么这个锐角所对的直角边等于斜边的一半.
几何语言:
课堂练习
如图,在Rt△ABC中,∠C=Rt∠,完成下面的填空:
(1)比较大小:AC_____AB
(
)
(2)∠A+∠B=______.(
)
(3)若∠A=30°,
∠B=_______.
直角三角形的性质定理1:
直角三角形的两个锐角互余
几何语言:
∵∠C=900
∴∠A+∠B=900
<
垂线段最短
900
三角形的内角和是1800
600
课堂练习
【例1】 如图,在Rt△ABC中,CD是斜边AB上的中线,∠CDA=70°,求∠A与∠B的度数.
?
1、如图,在Rt△ABC中,∠ACB=900,CD是中线。
(1)若CD=5cm,则AB=_____cm.
(2)若∠CDA=1000,则∠A=____,∠B=______.
(3)若AB=2cm,
∠A=300,则
CD=
,BC=____.
10
400
500
1cm
1cm
课堂练习
5、如图,已知Rt△ABC中,∠C=900,∠A=300,AC=10,沿DE折叠,使得点A与点B重合,则折痕DE的长为_______.
6、如图,在△ABC中,
∠ACB=900,CD⊥AB于D,
∠A=300,则AD的值为(
)
A.
4BD
B.
3BD
C.
2BD
D.
BD
B
课堂练习
4、如图是一副三角尺拼成的四边形ABCD,E为BD的中点.点E与点A,C的距离相等吗?请说明理由.
变式1:
如图,已知AD⊥CD,AB⊥BC,E为AC的中点,
试判断DE与BE是否相等,并说明理由.
变式2:
如图,已知AD⊥BD,AC⊥BC,E为AB的中点,
试判断DE与CE是否相等,并说明理由
变式3:如图,已知AD、BE分别是△ABC的BC、AC边上
的高,F是DE的中点,G是AB的中点,则FG⊥DE,请说明理由。
课堂练习
1、如图,一电线杆AB的拉线BC长为10m,当太阳光线与地面的夹角为600时,其影长AC=______.
2、如图,在△ABC中,AB=AC=20,∠ABC=∠ACB=150,CD是腰AB上的高,则CD的长为_______.
3、如图,Rt△ABC中,∠B=900,
∠ACB=600,延长BC到点D,使CD=AC,则AC与BD的长度之比为(
)
A.1:1
B.3:1
C.4:1
D.2:3
5m
10
D
课堂小结
一、这节课你掌握了哪些知识?
直角三角形的性质1:
直角三角形的两个锐角互余.
直角三角形的性质2:
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质3:
在直角三角形中,如果一个锐角等于300,那么这个锐角所对的直角边等于斜边的一半.
二、这节课你学会了哪些方法和技能?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
直角三角形
浙教版
八年级
新知导入
斜边
直角边
两个图中的△ABC具有怎样的共同特点?它们是什么特殊的三角形?
有一个角是直角的三角形叫直角三角形.
直角三角形用符号“Rt△“表示,如上图中的直角三角形△ABC记作:
Rt△ABC
新知讲解
拓展延伸
1、在直角三角形中,有一个锐角为52.5°,那么另一个锐角的度数为______.
2、在Rt△ABC中,∠C=90°,∠A-∠B=40°,那么∠A=_____,∠B=_____.
37.50
650
250
3、如图,在Rt△ABC中,∠ACB=900,CD⊥AB.
(1)图中互余的角有___对,分别是_________________________________________.
(2)相等的锐角有______对,分别是_______________.
4
∠A与∠B
∠A与∠1
∠2与∠B
∠1与∠2
2
∠1=∠B,
∠2=∠A
新知讲解
如图,已知Rt△ABC,画一条线段把Rt△ABC分成两个等腰三角形.
小明说:当∠A=450时我会画,我的画法是:过点C画直线CD,交AB于D,使∠ACD=∠
A=450,则线段CD即为所求.
小亮说:当∠A=300时我也会画,我的画法是:过点C画直线CD,交AB于D,使∠ACD=∠
A=
300,则线段CD即为所求.
当∠A的度数任意时,你能画出这条线段吗?若能,说说你的画法.
图中你能证明△DCB是等腰三角形吗?图中的线段CD是直角三角形的什么线?
CD与AB有什么数量关系?由此你有什么发现?
新知讲解
直角三角形的性质定理2:
直角三角形斜边上的中线等于斜边的一半.
几何语言:
新知讲解
直角三角形的性质定理3:
在直角三角形中,如果一个锐角等于300,那么这个锐角所对的直角边等于斜边的一半.
几何语言:
课堂练习
如图,在Rt△ABC中,∠C=Rt∠,完成下面的填空:
(1)比较大小:AC_____AB
(
)
(2)∠A+∠B=______.(
)
(3)若∠A=30°,
∠B=_______.
直角三角形的性质定理1:
直角三角形的两个锐角互余
几何语言:
∵∠C=900
∴∠A+∠B=900
<
垂线段最短
900
三角形的内角和是1800
600
课堂练习
【例1】 如图,在Rt△ABC中,CD是斜边AB上的中线,∠CDA=70°,求∠A与∠B的度数.
?
1、如图,在Rt△ABC中,∠ACB=900,CD是中线。
(1)若CD=5cm,则AB=_____cm.
(2)若∠CDA=1000,则∠A=____,∠B=______.
(3)若AB=2cm,
∠A=300,则
CD=
,BC=____.
10
400
500
1cm
1cm
课堂练习
5、如图,已知Rt△ABC中,∠C=900,∠A=300,AC=10,沿DE折叠,使得点A与点B重合,则折痕DE的长为_______.
6、如图,在△ABC中,
∠ACB=900,CD⊥AB于D,
∠A=300,则AD的值为(
)
A.
4BD
B.
3BD
C.
2BD
D.
BD
B
课堂练习
4、如图是一副三角尺拼成的四边形ABCD,E为BD的中点.点E与点A,C的距离相等吗?请说明理由.
变式1:
如图,已知AD⊥CD,AB⊥BC,E为AC的中点,
试判断DE与BE是否相等,并说明理由.
变式2:
如图,已知AD⊥BD,AC⊥BC,E为AB的中点,
试判断DE与CE是否相等,并说明理由
变式3:如图,已知AD、BE分别是△ABC的BC、AC边上
的高,F是DE的中点,G是AB的中点,则FG⊥DE,请说明理由。
课堂练习
1、如图,一电线杆AB的拉线BC长为10m,当太阳光线与地面的夹角为600时,其影长AC=______.
2、如图,在△ABC中,AB=AC=20,∠ABC=∠ACB=150,CD是腰AB上的高,则CD的长为_______.
3、如图,Rt△ABC中,∠B=900,
∠ACB=600,延长BC到点D,使CD=AC,则AC与BD的长度之比为(
)
A.1:1
B.3:1
C.4:1
D.2:3
5m
10
D
课堂小结
一、这节课你掌握了哪些知识?
直角三角形的性质1:
直角三角形的两个锐角互余.
直角三角形的性质2:
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质3:
在直角三角形中,如果一个锐角等于300,那么这个锐角所对的直角边等于斜边的一半.
二、这节课你学会了哪些方法和技能?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
