第1章 三角形的初步知识习题精选(含解析)
文档属性
| 名称 | 第1章 三角形的初步知识习题精选(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-26 21:23:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版八年级上 三角形的初步认识习题精选
一.选择题(共12小题)
1.三角形的两边分别为6,10,则第三边的长可能等于( )
A.3 B.11 C.16 D.17
2.下列命题:
(1)如果a<0,b>0,那么a+b<0;(2)相等的角是对顶角;(3)同角的补角相等;(4)如果两条直线被第三条直线所截,那么同位角相等.其中真命题的个数是( )
A.0 B.1 C.2 D.3
3.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.有一个内角是直角的三角形是直角三角形
C.任意三角形的外角和都是360°
D.三角形的中线、角平分线,高线都是线段
4.如图,△ABC的中线AD、BE相交于点F,若△ABF的面积是4,则四边形FDCE的面积是( )
A.4 B.4.5 C.3.5 D.5
5.在下列条件中,能确定△ABC是直角三角形的条件有( )
①∠A+∠B=∠C,
②∠A:∠B:∠C=1:2:3,
③∠A=90°﹣∠B,
④∠A=∠B=∠C中,
A.1个 B.2个 C.3个 D.4个
6.如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
7.如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,则∠AEB的度数为( )
A.100° B.110° C.120° D.130°
8.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
9.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:其中正确的是( )
①AC=AF,
②∠FAB=∠EAB,
③EF=BC,
④∠EAB=∠FAC,
A.①② B.①③④ C.①②③④ D.①③
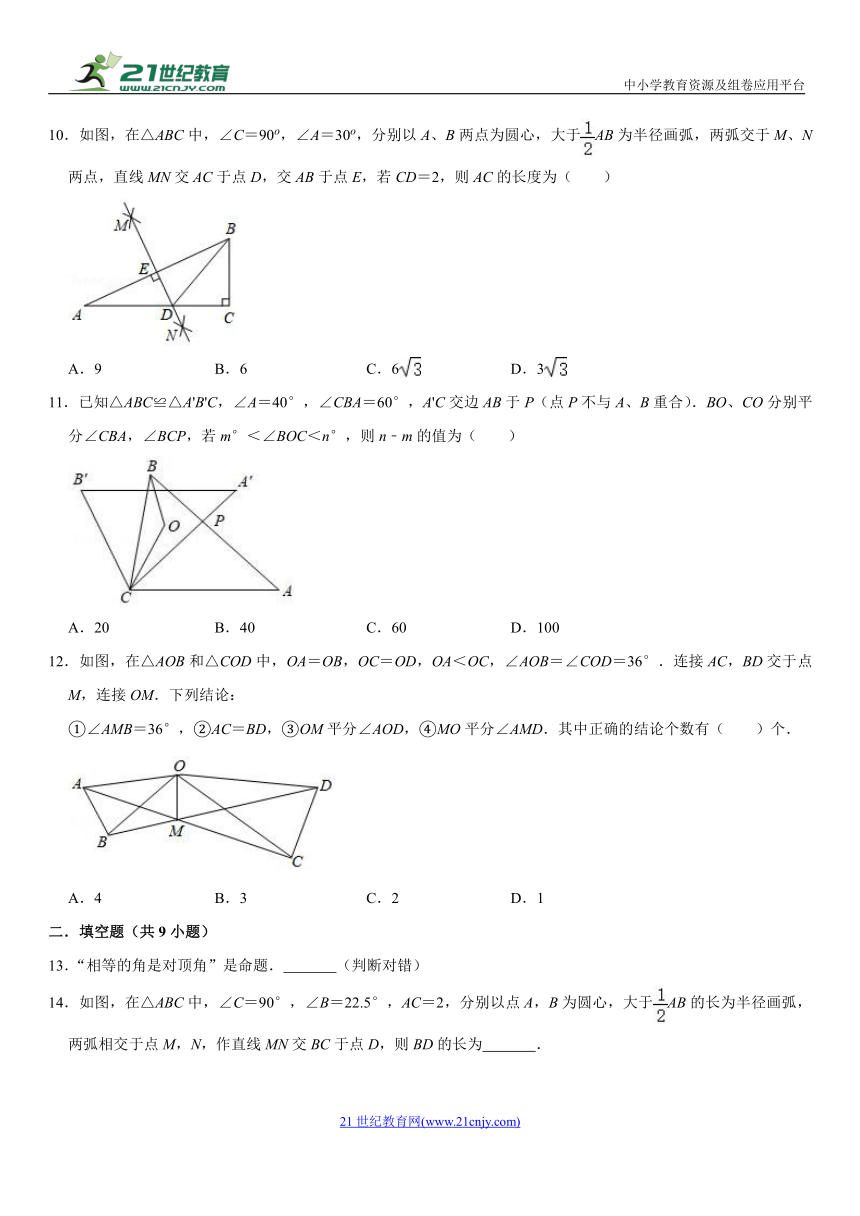
10.如图,在△ABC中,∠C=90o,∠A=30o,分别以A、B两点为圆心,大于AB为半径画弧,两弧交于M、N两点,直线MN交AC于点D,交AB于点E,若CD=2,则AC的长度为( )
A.9 B.6 C.6 D.3
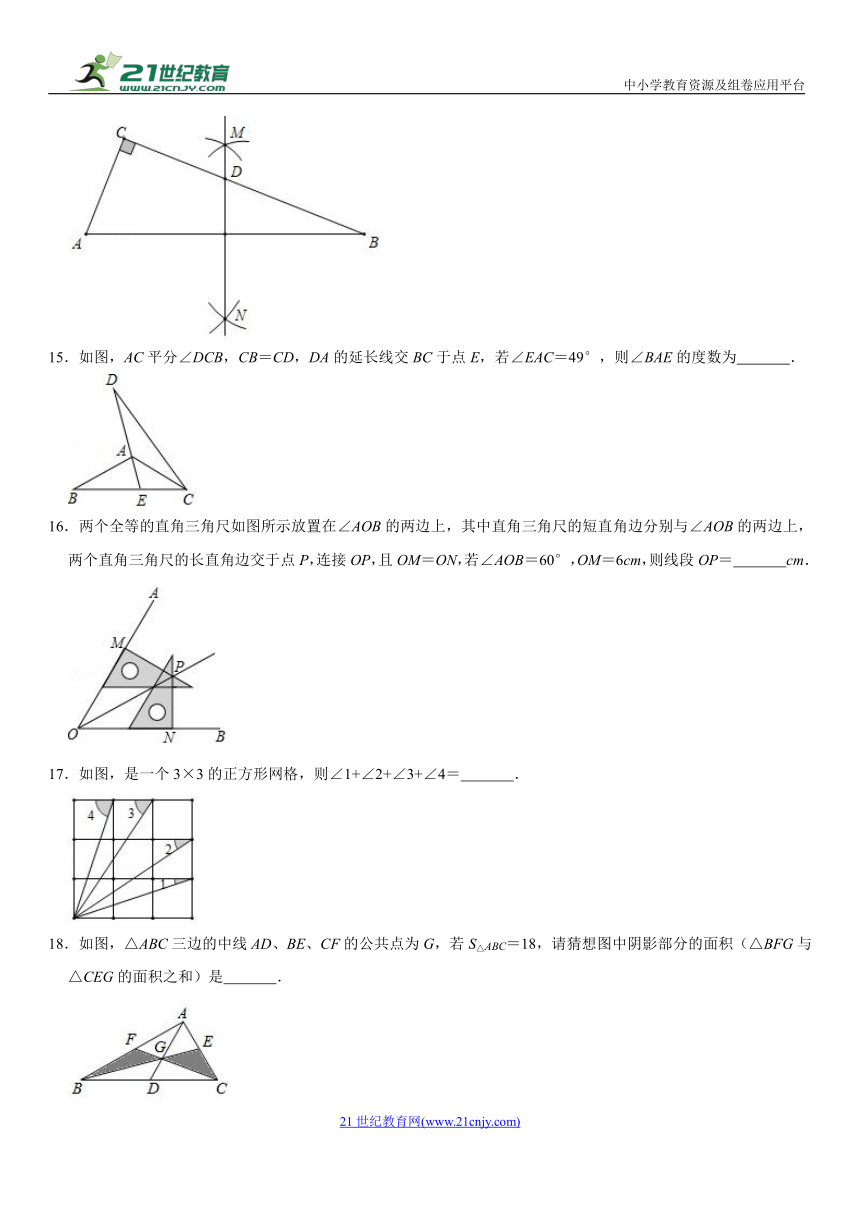
11.已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
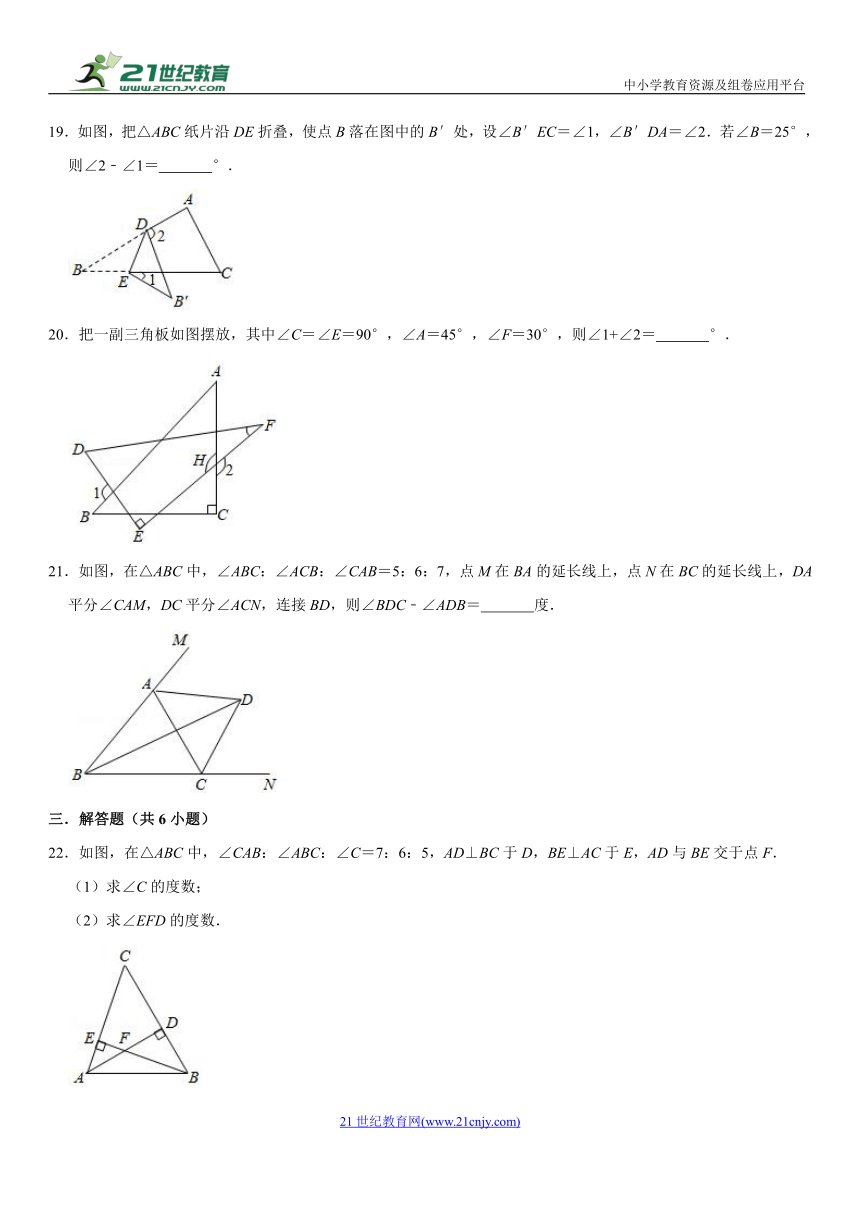
12.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
二.填空题(共9小题)
13.“相等的角是对顶角”是命题. (判断对错)
14.如图,在△ABC中,∠C=90°,∠B=22.5°,AC=2,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,则BD的长为 .
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
16.两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= cm.
17.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= .
18.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=18,请猜想图中阴影部分的面积(△BFG与△CEG的面积之和)是 .
19.如图,把△ABC纸片沿DE折叠,使点B落在图中的B′处,设∠B′EC=∠1,∠B′DA=∠2.若∠B=25°,则∠2﹣∠1= °.
20.把一副三角板如图摆放,其中∠C=∠E=90°,∠A=45°,∠F=30°,则∠1+∠2= °.
21.如图,在△ABC中,∠ABC:∠ACB:∠CAB=5:6:7,点M在BA的延长线上,点N在BC的延长线上,DA平分∠CAM,DC平分∠ACN,连接BD,则∠BDC﹣∠ADB= 度.
三.解答题(共6小题)
22.如图,在△ABC中,∠CAB:∠ABC:∠C=7:6:5,AD⊥BC于D,BE⊥AC于E,AD与BE交于点F.
(1)求∠C的度数;
(2)求∠EFD的度数.
23.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
24.如图,∠B=∠D,∠CAD=∠BAE,BC=DE.求证:AB=AD.
25.已知△ABC,P是平面内任意一点(A、B、C、P中任意三点都不在同一直线上).连接PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.
(1)如图,当点P在△ABC内时,
①若y=70,s=10,t=20,则x= ;
②探究s、t、x、y之间的数量关系,并证明你得到的结论.
(2)当点P在△ABC外时,直接写出s、t、x、y之间所有可能的数量关系,并画出相应的图形.
26.如图,在5×7的正方形网格中,已知△ABC的顶点B,C均在格点上,顶点A在小正方形的边上(不在格点),要求仅用一把无刻度的直尺,且不能用直尺中的直角完成下列作图,
(1)在图中作△ABC的边BC上的高线AD.
(2)在图中过点A作一直线,使它将△ABC的面积分成1:2的两部分.
27.已知:如图,在Rt△ABC中,∠ACB=90°,点D为BC边的中点.
(1)过点D作直线DE⊥BC,交线段AB于点E(要求:尺规作图,保留作图痕迹,标明字母,不写作法);
(2)在(1)的条件下,连接CE,求证:AE=CE.
浙教版八年级上 三角形的初步认识习题精选
参考答案与试题解析
一.选择题(共12小题)
1.三角形的两边分别为6,10,则第三边的长可能等于( )
A.3 B.11 C.16 D.17
【解答】解:设第三边的长为x,根据三角形的三边关系得:
10﹣6<x<10+6,
即4<x<16,
则第三边的长可能等于:11.
故选:B.
2.下列命题:
(1)如果a<0,b>0,那么a+b<0;(2)相等的角是对顶角;(3)同角的补角相等;(4)如果两条直线被第三条直线所截,那么同位角相等.其中真命题的个数是( )
A.0 B.1 C.2 D.3
【解答】解:如果a=﹣1,b=2,则a+b>0,所以(1)为假命题;
相等的角不一定对顶角,所以(2)为假命题;
同角的补角相等,所以(3)为真命题;
如果两条平行直线被第三条直线所截,那么同位角相等.所以(4)为假命题.
故选:B.
3.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.有一个内角是直角的三角形是直角三角形
C.任意三角形的外角和都是360°
D.三角形的中线、角平分线,高线都是线段
【解答】解:A.三角形的一个外角大于和它不相邻的任何一个内角,故本选项错误;
B.有一个内角是直角的三角形是直角三角形,故本选项正确;
C.任意三角形的外角和都是360°,故本选项正确;
D.三角形的中线、角平分线,高线都是线段,故本选项正确;
故选:A.
4.如图,△ABC的中线AD、BE相交于点F,若△ABF的面积是4,则四边形FDCE的面积是( )
A.4 B.4.5 C.3.5 D.5
【解答】解:∵△ABC的中线AD、BE相交于点F,
∴BD=CD,点F为△ABC的重心,
∴BF=2EF,AF=2FD,
∴S△BFD=S△ABF=×4=2,S△AEF=S△ABF=×4=2,
∵S△ABD=S△ACD=4+2=6,
∴四边形FDCE的面积=6﹣2=4.
故选:A.
5.在下列条件中,能确定△ABC是直角三角形的条件有( )
①∠A+∠B=∠C,
②∠A:∠B:∠C=1:2:3,
③∠A=90°﹣∠B,
④∠A=∠B=∠C中,
A.1个 B.2个 C.3个 D.4个
【解答】解:①∵∠A+∠B=∠C,且∠A+∠B+∠C=180°,
∴∠C+∠C=180°,即∠C=90°,
此时△ABC为直角三角形,①符合题意;
②∵∠A:∠B:∠C=1:2:3,
∴∠A+∠B=∠C,同①,
此时△ABC为直角三角形,②符合题意;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=90°,③符合题意;
④∵∠A=∠B=∠C,且∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°,
∴ABC为等边三角形,④不符合题意;
综上可知:①②③能确定△ABC为直角三角形.
故选:C.
6.如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
【解答】解:设∠ADB′=γ,∠AGC′=β,∠CEB′=y,∠C′FE=x,
∵DB′∥GC′,
∴γ+β=∠B+∠C=α,
∵EB′∥FG,
∴∠CFG=∠GFC′=y,
∴x+2y=180° ①,
∵γ+y=2∠B,β+x=2∠C,
∴γ+y+β+x=2α,
∴x+y=α②,
②×2﹣①可得x=2α﹣180°,
∴∠C′FE=2α﹣180°.
故选:D.
7.如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,则∠AEB的度数为( )
A.100° B.110° C.120° D.130°
【解答】解:∵BE∥AD,
∴∠ABE=∠BAD=20°,
∵BE平分∠ABC,
∴∠EBC=∠ABE=20°,
∵∠C=90°,
∴∠AEB=∠C+∠CBE=90°+20°=110°,
故选:B.
8.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC=90°,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:D.
9.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:其中正确的是( )
①AC=AF,
②∠FAB=∠EAB,
③EF=BC,
④∠EAB=∠FAC,
A.①② B.①③④ C.①②③④ D.①③
【解答】解:∵△ABC≌△AEF,
∴AC=AF,EF=CB,∠EAF=∠BAC,
∴∠EAF﹣∠BAF=∠BAC﹣∠BAF,
∴∠EAB=∠FAC,
正确的是①③④,
故选:B.
10.如图,在△ABC中,∠C=90o,∠A=30o,分别以A、B两点为圆心,大于AB为半径画弧,两弧交于M、N两点,直线MN交AC于点D,交AB于点E,若CD=2,则AC的长度为( )
A.9 B.6 C.6 D.3
【解答】解:由作法得MN垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∴∠BDC=30°+30°=60°,
在Rt△BDC中,BD=2CD=2×2=4,
∴AD=4,
∴AC=AD+CD=4+2=6.
故选:B.
11.已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
【解答】解:∵BO、CO分别平分∠ABC、∠PCB,
∴∠OBC=∠ABC,∠OCB=∠PCB,
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(∠ABC+∠PCB),
=180°﹣(180°﹣∠BPC),
=90°+∠BPC=90°+(∠A+∠ACP),
=110°+∠ACP,
∵∠A=40°,∠CBA=60°,
∴∠ACB=180°﹣∠A﹣∠CBA=180°﹣40°﹣60°=80°,
∵P点在AB边上且不与A、B重合,
∴0°<∠ACP<80°,
∴0°<2∠BOC﹣220°<80°,
∴110°<∠BOC<150°,
∴m=110,n=150.
∴n﹣m=40.
故选:B.
12.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
【解答】解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,故②正确;
∵∠OCA=∠ODB,
由三角形的外角性质得:
∠CMD+∠OCA=∠COD+∠ODB,
得出∠CMD=∠COD=36°,∠AMB=∠CMD=36°,故①正确;
作OG⊥AM于G,OH⊥DM于H,如图所示,
则∠OGA=∠OHB=90°,
在△OGA和△OHB中,
∵,
∴△OGA≌△OHB(AAS),
∴OG=OH,
∴OM平分∠AMD,故④正确;
假设OM平分∠AOD,则∠DOM=∠AOM,
在△AMO与△DMO中,
,
∴△AMO≌△OMD(ASA),
∴AO=OD,
∵OC=OD,
∴OA=OC,
而OA<OC,故③错误;
正确的个数有3个;
故选:B.
二.填空题(共9小题)
13.“相等的角是对顶角”是命题. 对 (判断对错)
【解答】解:判断一件事情的语句,叫做命题,所以相等的角是对顶角是命题,对
故答案为:对.
14.如图,在△ABC中,∠C=90°,∠B=22.5°,AC=2,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,则BD的长为 2 .
【解答】解:由作法得MN垂直平分AB,连接AD,则DA=DB,
∴∠DAB=∠B=22.5°,
∴∠CDA=22.5°+22.5°=45°,
∵∠C=90°,
∴△ACD为等腰直角三角形,
∴AD=AC=2,
∴BD=2.
故答案为2.
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 82° .
【解答】解:∵AC平分∠DCB,
∴∠BCA=∠DCA,
∵CB=CD,
∵AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=49°,
∴∠B+∠ACB=49°,
∴∠BAE=180°﹣∠B﹣∠ACB﹣∠CAE=82°,
故答案为:82°.
16.两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= 4 cm.
【解答】解:在Rt△OMP和Rt△ONP中,OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∵∠AOB=60°,
∴∠MOP=∠NOP=30°,
∵∠OMP=90°,
∴OP=2MP,OM=MP=6cm,
∴MP=2cm,
∴OP=4cm,
故答案为:4.
17.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= 180° .
【解答】解:∵∠1和∠4所在的三角形全等,
∴∠1+∠4=90°,
∵∠2和∠3所在的三角形全等,
∴∠2+∠3=90°,
∴∠1+∠2+∠3十∠4=180°.
故答案为:180°.
18.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=18,请猜想图中阴影部分的面积(△BFG与△CEG的面积之和)是 6 .
【解答】解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×18=9,
∴S△CGE=S△ACF=×9=3,S△BGF=S△BCF=×9=3,
∴S阴影=S△CGE+S△BGF=6.
故答案为6.
19.如图,把△ABC纸片沿DE折叠,使点B落在图中的B′处,设∠B′EC=∠1,∠B′DA=∠2.若∠B=25°,则∠2﹣∠1= 50 °.
【解答】解:∵∠B=25°,
∴∠B′=∠B=25°,
∵∠3=∠1+∠B′=∠1+25°,
∵∠2=∠3+∠B=∠1+25°+25°,
∴∠2﹣∠1=50°,
故答案为50.
20.把一副三角板如图摆放,其中∠C=∠E=90°,∠A=45°,∠F=30°,则∠1+∠2= 225 °.
【解答】解:∵∠C=∠E=90°,∠A=45°,∠F=30°,
∴∠D=60°,
∵∠1+∠2=∠D+∠3+∠F+∠6,∠3=∠4,∠5=∠6,∠4+∠5=180°﹣∠A
∴∠1+∠2=∠D+∠F+∠4+∠5
=∠D+∠F+180°﹣∠A
=60°+30°+180°﹣45°
=225°,
故答案为:225.
21.如图,在△ABC中,∠ABC:∠ACB:∠CAB=5:6:7,点M在BA的延长线上,点N在BC的延长线上,DA平分∠CAM,DC平分∠ACN,连接BD,则∠BDC﹣∠ADB= 5 度.
【解答】解:过D作DE⊥BM于E,DH⊥AC于H,DF⊥BN于F,
∵DA平分∠CAM,DC平分∠ACN,
∴DE=DH,DH=DF,
∴DE=DF,
∴BD平分∠ABC,
∵在△ABC中,∠ABC:∠ACB:∠CAB=5:6:7,
∴设∠ABC=5x,∠ACB=6x,∠CAB=7x,
∵∠ABC+∠BAC+∠ACB=180°,
∴5x+6x+7x=180°,
∴x=10°,
∴∠ABC=50°,∠ACB=60°,∠CAB=70°,
∴∠MAC=110°,∠ACN=120°,
∵DA平分∠CAM,DC平分∠ACN,
∴∠MAD=MAC=55°,∠NCD=ACN=60°,∠ABD=∠CBD=25°,
∴∠BDC=∠NCD﹣∠DBC,∠ADB=∠MAD﹣∠ABD,
∴∠BDC﹣∠ADB=∠NCD﹣∠DBC﹣(∠MAD﹣∠ABD)=∠NCD﹣∠MAD=60°﹣55°=5°,
故答案为:5.
三.解答题(共6小题)
22.如图,在△ABC中,∠CAB:∠ABC:∠C=7:6:5,AD⊥BC于D,BE⊥AC于E,AD与BE交于点F.
(1)求∠C的度数;
(2)求∠EFD的度数.
【解答】解:(1)设∠CAB=7x,则∠ABC=6x,∠C=5x.
∵∠CAB+∠ABC+∠C=180°,
∴7x+6x+5x=180°,
∴x=10°,
∴∠C=5x=50°.
(2)∵AD⊥BC,BE⊥AC,
∴∠BEC=90°,∠ADC=90°,
又∵∠BEC+∠EFD+∠ADC+∠C=360°,
∴∠EFD=360°﹣90°﹣90°﹣50°=130°.
23.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
【解答】解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
24.如图,∠B=∠D,∠CAD=∠BAE,BC=DE.求证:AB=AD.
【解答】证明:∵∠CAD=∠BAE,
∴∠CAD+∠DAB=∠BAE+∠DAB,
即∠CAB=∠EAD,
又∵∠B=∠D,BC=DE,
∴△BAC≌△DAE(AAS),
∴AB=AD.
25.已知△ABC,P是平面内任意一点(A、B、C、P中任意三点都不在同一直线上).连接PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.
(1)如图,当点P在△ABC内时,
①若y=70,s=10,t=20,则x= 100 ;
②探究s、t、x、y之间的数量关系,并证明你得到的结论.
(2)当点P在△ABC外时,直接写出s、t、x、y之间所有可能的数量关系,并画出相应的图形.
【解答】解:(1)①∵∠BAC=70°,
∴∠ABC+∠ACB=110°,
∵∠PBA=10°,∠PCA=20°,
∴∠PBC+∠PCB=80°,
∴∠BPC=100°,
∴x=100,
故答案为100.
②结论:x=y+s+t.
理由:∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°,∠PBC+∠PCB+∠BPC=180°,
∴∠A+∠PBA+∠PCA=∠BPC,
∴x=y+s+t.
(2)s、t、x、y之间所有可能的数量关系:
如图1:s+x=t+y;
如图2:s+y=t+x;
如图3:y=x+s+t;
如图4:x+y+s+t=360°;
如图5:t=s+x+y;
如图6:s=t+x+y;
.
26.如图,在5×7的正方形网格中,已知△ABC的顶点B,C均在格点上,顶点A在小正方形的边上(不在格点),要求仅用一把无刻度的直尺,且不能用直尺中的直角完成下列作图,
(1)在图中作△ABC的边BC上的高线AD.
(2)在图中过点A作一直线,使它将△ABC的面积分成1:2的两部分.
【解答】解:(1)如图1中,线段AD即为所求.
(2)如图2中,直线AE即为所求.
27.已知:如图,在Rt△ABC中,∠ACB=90°,点D为BC边的中点.
(1)过点D作直线DE⊥BC,交线段AB于点E(要求:尺规作图,保留作图痕迹,标明字母,不写作法);
(2)在(1)的条件下,连接CE,求证:AE=CE.
【解答】解:(1)如图所示,直线DE即为所求;
(2)∵点D为BC边的中点,DE⊥BC,
∴BE=CE,
∴∠B=∠BCE,
∵∠ACB=90°,
∴∠B+∠A=90°,∠BCE+∠ACE=90°,
∴∠A=∠ACE,
∴AE=CE.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/7/25 21:26:41;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
浙教版八年级上 三角形的初步认识习题精选
一.选择题(共12小题)
1.三角形的两边分别为6,10,则第三边的长可能等于( )
A.3 B.11 C.16 D.17
2.下列命题:
(1)如果a<0,b>0,那么a+b<0;(2)相等的角是对顶角;(3)同角的补角相等;(4)如果两条直线被第三条直线所截,那么同位角相等.其中真命题的个数是( )
A.0 B.1 C.2 D.3
3.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.有一个内角是直角的三角形是直角三角形
C.任意三角形的外角和都是360°
D.三角形的中线、角平分线,高线都是线段
4.如图,△ABC的中线AD、BE相交于点F,若△ABF的面积是4,则四边形FDCE的面积是( )
A.4 B.4.5 C.3.5 D.5
5.在下列条件中,能确定△ABC是直角三角形的条件有( )
①∠A+∠B=∠C,
②∠A:∠B:∠C=1:2:3,
③∠A=90°﹣∠B,
④∠A=∠B=∠C中,
A.1个 B.2个 C.3个 D.4个
6.如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
7.如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,则∠AEB的度数为( )
A.100° B.110° C.120° D.130°
8.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
9.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:其中正确的是( )
①AC=AF,
②∠FAB=∠EAB,
③EF=BC,
④∠EAB=∠FAC,
A.①② B.①③④ C.①②③④ D.①③
10.如图,在△ABC中,∠C=90o,∠A=30o,分别以A、B两点为圆心,大于AB为半径画弧,两弧交于M、N两点,直线MN交AC于点D,交AB于点E,若CD=2,则AC的长度为( )
A.9 B.6 C.6 D.3
11.已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
12.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
二.填空题(共9小题)
13.“相等的角是对顶角”是命题. (判断对错)
14.如图,在△ABC中,∠C=90°,∠B=22.5°,AC=2,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,则BD的长为 .
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
16.两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= cm.
17.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= .
18.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=18,请猜想图中阴影部分的面积(△BFG与△CEG的面积之和)是 .
19.如图,把△ABC纸片沿DE折叠,使点B落在图中的B′处,设∠B′EC=∠1,∠B′DA=∠2.若∠B=25°,则∠2﹣∠1= °.
20.把一副三角板如图摆放,其中∠C=∠E=90°,∠A=45°,∠F=30°,则∠1+∠2= °.
21.如图,在△ABC中,∠ABC:∠ACB:∠CAB=5:6:7,点M在BA的延长线上,点N在BC的延长线上,DA平分∠CAM,DC平分∠ACN,连接BD,则∠BDC﹣∠ADB= 度.
三.解答题(共6小题)
22.如图,在△ABC中,∠CAB:∠ABC:∠C=7:6:5,AD⊥BC于D,BE⊥AC于E,AD与BE交于点F.
(1)求∠C的度数;
(2)求∠EFD的度数.
23.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
24.如图,∠B=∠D,∠CAD=∠BAE,BC=DE.求证:AB=AD.
25.已知△ABC,P是平面内任意一点(A、B、C、P中任意三点都不在同一直线上).连接PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.
(1)如图,当点P在△ABC内时,
①若y=70,s=10,t=20,则x= ;
②探究s、t、x、y之间的数量关系,并证明你得到的结论.
(2)当点P在△ABC外时,直接写出s、t、x、y之间所有可能的数量关系,并画出相应的图形.
26.如图,在5×7的正方形网格中,已知△ABC的顶点B,C均在格点上,顶点A在小正方形的边上(不在格点),要求仅用一把无刻度的直尺,且不能用直尺中的直角完成下列作图,
(1)在图中作△ABC的边BC上的高线AD.
(2)在图中过点A作一直线,使它将△ABC的面积分成1:2的两部分.
27.已知:如图,在Rt△ABC中,∠ACB=90°,点D为BC边的中点.
(1)过点D作直线DE⊥BC,交线段AB于点E(要求:尺规作图,保留作图痕迹,标明字母,不写作法);
(2)在(1)的条件下,连接CE,求证:AE=CE.
浙教版八年级上 三角形的初步认识习题精选
参考答案与试题解析
一.选择题(共12小题)
1.三角形的两边分别为6,10,则第三边的长可能等于( )
A.3 B.11 C.16 D.17
【解答】解:设第三边的长为x,根据三角形的三边关系得:
10﹣6<x<10+6,
即4<x<16,
则第三边的长可能等于:11.
故选:B.
2.下列命题:
(1)如果a<0,b>0,那么a+b<0;(2)相等的角是对顶角;(3)同角的补角相等;(4)如果两条直线被第三条直线所截,那么同位角相等.其中真命题的个数是( )
A.0 B.1 C.2 D.3
【解答】解:如果a=﹣1,b=2,则a+b>0,所以(1)为假命题;
相等的角不一定对顶角,所以(2)为假命题;
同角的补角相等,所以(3)为真命题;
如果两条平行直线被第三条直线所截,那么同位角相等.所以(4)为假命题.
故选:B.
3.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.有一个内角是直角的三角形是直角三角形
C.任意三角形的外角和都是360°
D.三角形的中线、角平分线,高线都是线段
【解答】解:A.三角形的一个外角大于和它不相邻的任何一个内角,故本选项错误;
B.有一个内角是直角的三角形是直角三角形,故本选项正确;
C.任意三角形的外角和都是360°,故本选项正确;
D.三角形的中线、角平分线,高线都是线段,故本选项正确;
故选:A.
4.如图,△ABC的中线AD、BE相交于点F,若△ABF的面积是4,则四边形FDCE的面积是( )
A.4 B.4.5 C.3.5 D.5
【解答】解:∵△ABC的中线AD、BE相交于点F,
∴BD=CD,点F为△ABC的重心,
∴BF=2EF,AF=2FD,
∴S△BFD=S△ABF=×4=2,S△AEF=S△ABF=×4=2,
∵S△ABD=S△ACD=4+2=6,
∴四边形FDCE的面积=6﹣2=4.
故选:A.
5.在下列条件中,能确定△ABC是直角三角形的条件有( )
①∠A+∠B=∠C,
②∠A:∠B:∠C=1:2:3,
③∠A=90°﹣∠B,
④∠A=∠B=∠C中,
A.1个 B.2个 C.3个 D.4个
【解答】解:①∵∠A+∠B=∠C,且∠A+∠B+∠C=180°,
∴∠C+∠C=180°,即∠C=90°,
此时△ABC为直角三角形,①符合题意;
②∵∠A:∠B:∠C=1:2:3,
∴∠A+∠B=∠C,同①,
此时△ABC为直角三角形,②符合题意;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=90°,③符合题意;
④∵∠A=∠B=∠C,且∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°,
∴ABC为等边三角形,④不符合题意;
综上可知:①②③能确定△ABC为直角三角形.
故选:C.
6.如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
【解答】解:设∠ADB′=γ,∠AGC′=β,∠CEB′=y,∠C′FE=x,
∵DB′∥GC′,
∴γ+β=∠B+∠C=α,
∵EB′∥FG,
∴∠CFG=∠GFC′=y,
∴x+2y=180° ①,
∵γ+y=2∠B,β+x=2∠C,
∴γ+y+β+x=2α,
∴x+y=α②,
②×2﹣①可得x=2α﹣180°,
∴∠C′FE=2α﹣180°.
故选:D.
7.如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,则∠AEB的度数为( )
A.100° B.110° C.120° D.130°
【解答】解:∵BE∥AD,
∴∠ABE=∠BAD=20°,
∵BE平分∠ABC,
∴∠EBC=∠ABE=20°,
∵∠C=90°,
∴∠AEB=∠C+∠CBE=90°+20°=110°,
故选:B.
8.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC=90°,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:D.
9.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:其中正确的是( )
①AC=AF,
②∠FAB=∠EAB,
③EF=BC,
④∠EAB=∠FAC,
A.①② B.①③④ C.①②③④ D.①③
【解答】解:∵△ABC≌△AEF,
∴AC=AF,EF=CB,∠EAF=∠BAC,
∴∠EAF﹣∠BAF=∠BAC﹣∠BAF,
∴∠EAB=∠FAC,
正确的是①③④,
故选:B.
10.如图,在△ABC中,∠C=90o,∠A=30o,分别以A、B两点为圆心,大于AB为半径画弧,两弧交于M、N两点,直线MN交AC于点D,交AB于点E,若CD=2,则AC的长度为( )
A.9 B.6 C.6 D.3
【解答】解:由作法得MN垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∴∠BDC=30°+30°=60°,
在Rt△BDC中,BD=2CD=2×2=4,
∴AD=4,
∴AC=AD+CD=4+2=6.
故选:B.
11.已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
【解答】解:∵BO、CO分别平分∠ABC、∠PCB,
∴∠OBC=∠ABC,∠OCB=∠PCB,
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(∠ABC+∠PCB),
=180°﹣(180°﹣∠BPC),
=90°+∠BPC=90°+(∠A+∠ACP),
=110°+∠ACP,
∵∠A=40°,∠CBA=60°,
∴∠ACB=180°﹣∠A﹣∠CBA=180°﹣40°﹣60°=80°,
∵P点在AB边上且不与A、B重合,
∴0°<∠ACP<80°,
∴0°<2∠BOC﹣220°<80°,
∴110°<∠BOC<150°,
∴m=110,n=150.
∴n﹣m=40.
故选:B.
12.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
【解答】解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,故②正确;
∵∠OCA=∠ODB,
由三角形的外角性质得:
∠CMD+∠OCA=∠COD+∠ODB,
得出∠CMD=∠COD=36°,∠AMB=∠CMD=36°,故①正确;
作OG⊥AM于G,OH⊥DM于H,如图所示,
则∠OGA=∠OHB=90°,
在△OGA和△OHB中,
∵,
∴△OGA≌△OHB(AAS),
∴OG=OH,
∴OM平分∠AMD,故④正确;
假设OM平分∠AOD,则∠DOM=∠AOM,
在△AMO与△DMO中,
,
∴△AMO≌△OMD(ASA),
∴AO=OD,
∵OC=OD,
∴OA=OC,
而OA<OC,故③错误;
正确的个数有3个;
故选:B.
二.填空题(共9小题)
13.“相等的角是对顶角”是命题. 对 (判断对错)
【解答】解:判断一件事情的语句,叫做命题,所以相等的角是对顶角是命题,对
故答案为:对.
14.如图,在△ABC中,∠C=90°,∠B=22.5°,AC=2,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,则BD的长为 2 .
【解答】解:由作法得MN垂直平分AB,连接AD,则DA=DB,
∴∠DAB=∠B=22.5°,
∴∠CDA=22.5°+22.5°=45°,
∵∠C=90°,
∴△ACD为等腰直角三角形,
∴AD=AC=2,
∴BD=2.
故答案为2.
15.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 82° .
【解答】解:∵AC平分∠DCB,
∴∠BCA=∠DCA,
∵CB=CD,
∵AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=49°,
∴∠B+∠ACB=49°,
∴∠BAE=180°﹣∠B﹣∠ACB﹣∠CAE=82°,
故答案为:82°.
16.两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= 4 cm.
【解答】解:在Rt△OMP和Rt△ONP中,OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∵∠AOB=60°,
∴∠MOP=∠NOP=30°,
∵∠OMP=90°,
∴OP=2MP,OM=MP=6cm,
∴MP=2cm,
∴OP=4cm,
故答案为:4.
17.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= 180° .
【解答】解:∵∠1和∠4所在的三角形全等,
∴∠1+∠4=90°,
∵∠2和∠3所在的三角形全等,
∴∠2+∠3=90°,
∴∠1+∠2+∠3十∠4=180°.
故答案为:180°.
18.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=18,请猜想图中阴影部分的面积(△BFG与△CEG的面积之和)是 6 .
【解答】解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×18=9,
∴S△CGE=S△ACF=×9=3,S△BGF=S△BCF=×9=3,
∴S阴影=S△CGE+S△BGF=6.
故答案为6.
19.如图,把△ABC纸片沿DE折叠,使点B落在图中的B′处,设∠B′EC=∠1,∠B′DA=∠2.若∠B=25°,则∠2﹣∠1= 50 °.
【解答】解:∵∠B=25°,
∴∠B′=∠B=25°,
∵∠3=∠1+∠B′=∠1+25°,
∵∠2=∠3+∠B=∠1+25°+25°,
∴∠2﹣∠1=50°,
故答案为50.
20.把一副三角板如图摆放,其中∠C=∠E=90°,∠A=45°,∠F=30°,则∠1+∠2= 225 °.
【解答】解:∵∠C=∠E=90°,∠A=45°,∠F=30°,
∴∠D=60°,
∵∠1+∠2=∠D+∠3+∠F+∠6,∠3=∠4,∠5=∠6,∠4+∠5=180°﹣∠A
∴∠1+∠2=∠D+∠F+∠4+∠5
=∠D+∠F+180°﹣∠A
=60°+30°+180°﹣45°
=225°,
故答案为:225.
21.如图,在△ABC中,∠ABC:∠ACB:∠CAB=5:6:7,点M在BA的延长线上,点N在BC的延长线上,DA平分∠CAM,DC平分∠ACN,连接BD,则∠BDC﹣∠ADB= 5 度.
【解答】解:过D作DE⊥BM于E,DH⊥AC于H,DF⊥BN于F,
∵DA平分∠CAM,DC平分∠ACN,
∴DE=DH,DH=DF,
∴DE=DF,
∴BD平分∠ABC,
∵在△ABC中,∠ABC:∠ACB:∠CAB=5:6:7,
∴设∠ABC=5x,∠ACB=6x,∠CAB=7x,
∵∠ABC+∠BAC+∠ACB=180°,
∴5x+6x+7x=180°,
∴x=10°,
∴∠ABC=50°,∠ACB=60°,∠CAB=70°,
∴∠MAC=110°,∠ACN=120°,
∵DA平分∠CAM,DC平分∠ACN,
∴∠MAD=MAC=55°,∠NCD=ACN=60°,∠ABD=∠CBD=25°,
∴∠BDC=∠NCD﹣∠DBC,∠ADB=∠MAD﹣∠ABD,
∴∠BDC﹣∠ADB=∠NCD﹣∠DBC﹣(∠MAD﹣∠ABD)=∠NCD﹣∠MAD=60°﹣55°=5°,
故答案为:5.
三.解答题(共6小题)
22.如图,在△ABC中,∠CAB:∠ABC:∠C=7:6:5,AD⊥BC于D,BE⊥AC于E,AD与BE交于点F.
(1)求∠C的度数;
(2)求∠EFD的度数.
【解答】解:(1)设∠CAB=7x,则∠ABC=6x,∠C=5x.
∵∠CAB+∠ABC+∠C=180°,
∴7x+6x+5x=180°,
∴x=10°,
∴∠C=5x=50°.
(2)∵AD⊥BC,BE⊥AC,
∴∠BEC=90°,∠ADC=90°,
又∵∠BEC+∠EFD+∠ADC+∠C=360°,
∴∠EFD=360°﹣90°﹣90°﹣50°=130°.
23.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
【解答】解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
24.如图,∠B=∠D,∠CAD=∠BAE,BC=DE.求证:AB=AD.
【解答】证明:∵∠CAD=∠BAE,
∴∠CAD+∠DAB=∠BAE+∠DAB,
即∠CAB=∠EAD,
又∵∠B=∠D,BC=DE,
∴△BAC≌△DAE(AAS),
∴AB=AD.
25.已知△ABC,P是平面内任意一点(A、B、C、P中任意三点都不在同一直线上).连接PB、PC,设∠PBA=s°,∠PCA=t°,∠BPC=x°,∠BAC=y°.
(1)如图,当点P在△ABC内时,
①若y=70,s=10,t=20,则x= 100 ;
②探究s、t、x、y之间的数量关系,并证明你得到的结论.
(2)当点P在△ABC外时,直接写出s、t、x、y之间所有可能的数量关系,并画出相应的图形.
【解答】解:(1)①∵∠BAC=70°,
∴∠ABC+∠ACB=110°,
∵∠PBA=10°,∠PCA=20°,
∴∠PBC+∠PCB=80°,
∴∠BPC=100°,
∴x=100,
故答案为100.
②结论:x=y+s+t.
理由:∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°,∠PBC+∠PCB+∠BPC=180°,
∴∠A+∠PBA+∠PCA=∠BPC,
∴x=y+s+t.
(2)s、t、x、y之间所有可能的数量关系:
如图1:s+x=t+y;
如图2:s+y=t+x;
如图3:y=x+s+t;
如图4:x+y+s+t=360°;
如图5:t=s+x+y;
如图6:s=t+x+y;
.
26.如图,在5×7的正方形网格中,已知△ABC的顶点B,C均在格点上,顶点A在小正方形的边上(不在格点),要求仅用一把无刻度的直尺,且不能用直尺中的直角完成下列作图,
(1)在图中作△ABC的边BC上的高线AD.
(2)在图中过点A作一直线,使它将△ABC的面积分成1:2的两部分.
【解答】解:(1)如图1中,线段AD即为所求.
(2)如图2中,直线AE即为所求.
27.已知:如图,在Rt△ABC中,∠ACB=90°,点D为BC边的中点.
(1)过点D作直线DE⊥BC,交线段AB于点E(要求:尺规作图,保留作图痕迹,标明字母,不写作法);
(2)在(1)的条件下,连接CE,求证:AE=CE.
【解答】解:(1)如图所示,直线DE即为所求;
(2)∵点D为BC边的中点,DE⊥BC,
∴BE=CE,
∴∠B=∠BCE,
∵∠ACB=90°,
∴∠B+∠A=90°,∠BCE+∠ACE=90°,
∴∠A=∠ACE,
∴AE=CE.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/7/25 21:26:41;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
