2.8 直角三角形全等的判定 同步练习(含解析)
文档属性
| 名称 | 2.8 直角三角形全等的判定 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-28 07:28:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册2.8 直角三角形全等的判定 同步练习
一、单选题
1.下列判定直角三角形全等的方法,不正确的是(??? )
A.?两条直角边对应相等。???????????????????????????????????????B.?斜边和一锐角对应相等。
C.?斜边和一条直角边对应相等。?????????????????????????????D.?两锐角相等。
2.如图,AC,BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.下列条件不能保证两个三角形全等的是(???? )
A.?三边对应相等??????????????????????????????????????????????????B.?两边一角对应相等
C.?两角一边对应相等???????????????????????????????????????????D.?直角边和一个锐角对应相等
4.如图△ABC和△DEF,下列条件中①∠B=∠E=90°,AC=DF;②∠B=∠E,AB=DE,AC=DF;③在Rt△ABC和Rt△DEF中,BC=EF,AC=DF;④∠A=∠D,∠B=∠E,∠C=∠F;⑤∠A=∠D,BC=EF,∠C=∠F,能证明△ABC≌△DEF的是(?? )
A.?③ ⑤????????????????????????????B.?① ③⑤????????????????????????????C.?①② ③⑤????????????????????????????D.?①② ③④⑤
5.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件(??? )
A.?∠BAC=∠BAD???????????B.?AC=AD或BC=BD???????????C.?AC=AD且BC=BD???????????D.?以上都不正确
6.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( ??)
A.?7???????????????????????????????????????????B.?5???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
7.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是(?? )
A.?AE=DF?????????????????????????????B.?∠A=∠D?????????????????????????????C.?∠B=∠C?????????????????????????????D.?AB=DC
8.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是(?? )
A.?HL??????????????????????????????????????B.?SAS??????????????????????????????????????C.?AAS??????????????????????????????????????D.?SSS
9.如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC于E、F两点,则阴影部分的面积是(? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
10.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE;④AD=AB+CD,四个结论中成立的是(? ??)
A.?①②④???????????????????????????B.?①②③?????????????????????????????????C.?②③④?????????????????????????????????D.?①③
二、填空题
11.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌________,全等的根据是________.
12.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB , P , Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=________时,△ABC和△PQA全等.
13.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 ________?cm.
14.如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D , DE⊥AB于E . 若△ADE的周长为8cm , 则AB=________ cm .
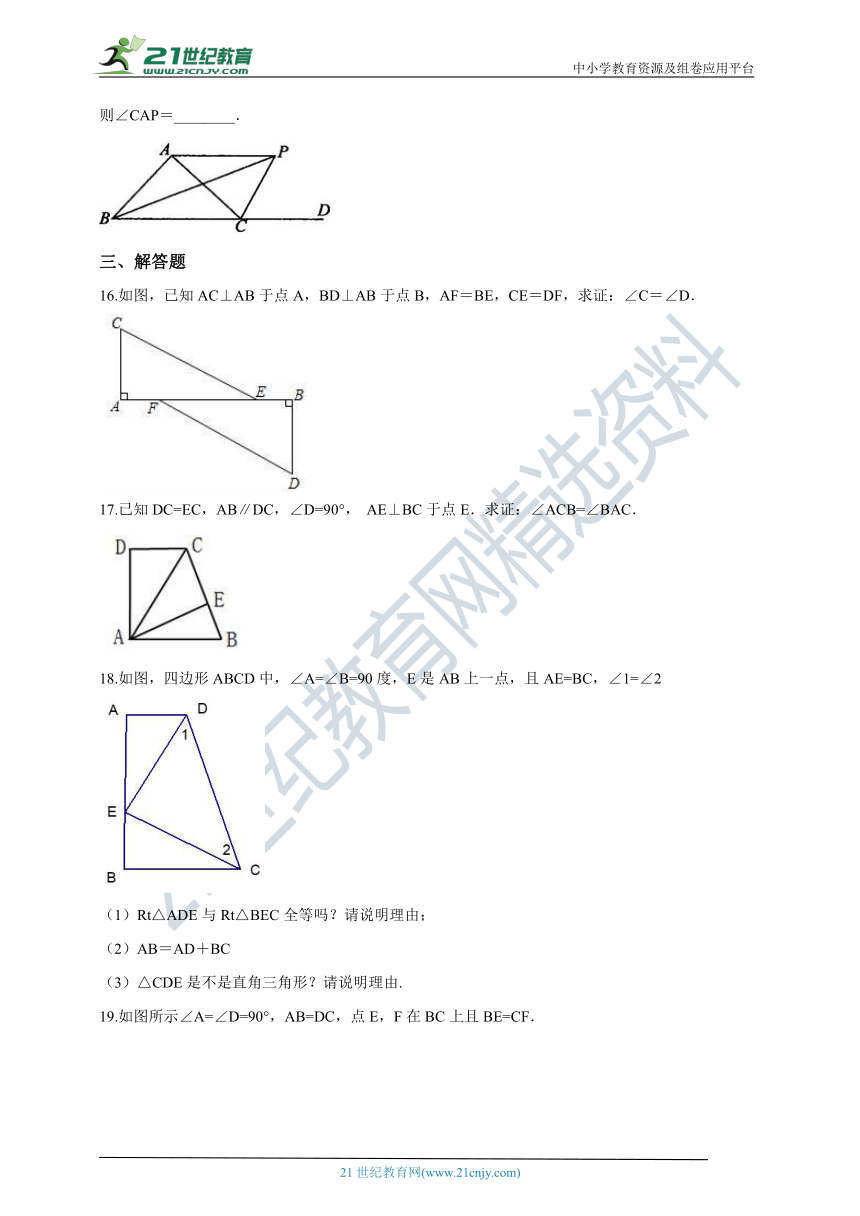
15.如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=________.
三、解答题
16.如图,已知AC⊥AB于点A,BD⊥AB于点B,AF=BE,CE=DF,求证:∠C=∠D.
17.已知DC=EC,AB∥DC,∠D=90°, AE⊥BC于点E.求证:∠ACB=∠BAC.
18.如图,四边形ABCD中,∠A=∠B=90度,E是AB上一点,且AE=BC,∠1=∠2
(1)Rt△ADE与Rt△BEC全等吗?请说明理由;
(2)AB=AD+BC
(3)△CDE是不是直角三角形?请说明理由.
19.如图所示∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
(1)求证:AF=DE.
(2)若PO⊥EF,求证:OP平分∠EOF.
答案解析部分
一、单选题
1. D
考点:直角三角形全等的判定
解:如果在两个直角三角形中,两条直角边对应相等,那么根据SAS即可判断两三角形全等,故答案为:A正确.
如果在两个直角三角形中,斜边和一锐角对应相等,那么根据AAS也可判断两三角形全等,故答案为:B正确.
如果在两个直角三角形中,斜边和一直角边对应相等,那么根据HL也可判断两三角形全等,故答案为:C正确.
如果在两个直角三角形中,两锐角相等,无法判断两三角形全等,故答案为:D错误.
故答案为:D.
分析:根据直角三角形全等的判定方法:SSS,SAS,ASA,AAS,HL即可一一判断得出答案.
2. D
考点:直角三角形全等的判定
解:根据矩形的性质,△CDA、△BAD、△DCB与△ABC全等,因为DE∥AC,所以∠CDE=∠DCA,因为CD=DC,∠ADC=∠ECD,所以△ADC≌△ECD,所以与△ABC全等的三角形有4个.
故答案为:D.
分析:根据题中条件,结合图形,可得出与△ABC全等的三角形为△ADC,△ABD,△DBC,△DCE共4个.
3. B
考点:直角三角形全等的判定
解:A、 三边对应相等 (SSS),则三角形全等,正确,不符合题意;
B、 两边一角对应相等?,无边边角定理,不能证明三角形全等,错误,不符合题意;
C、 两角一边对应相等(AAS),则三角形全等,正确,不符合题意;
D、 直角边和一个锐角对应相等 (ASA),则三角形全等,正确,不符合题意.
故答案为:B.
分析:三角形全等的判定定理有:边角边、角角边、角边角和边边边定理,逐项分析即可判断.
4. A
考点:直角三角形全等的判定
解:??①∠B=∠E=90°,AC=DF,只有两个要素对应相等不能证明三角形全等,不符合题意;
②∠B=∠E,AB=DE, AC=DF,无边边角定理,不能证明两三角形全等,不符合题意 ;
③在Rt△ABC和Rt△DEF中,BC=EF,AC=DF,则 △ABC≌△DEF (HL),符合题意;
④∠A=∠D,∠B=∠E,∠C=∠F,三个角对应相等,不能证明两三角形全等,不符合题意;
⑤∠A=∠D,BC=EF,∠C=∠F,则 △ABC≌△DEF(AAS)?, 符合题意;
综上,只有 ③⑤ 符合题意.
故答案为:A.
?分析:三角形全等的判定定理有:边角边、角角边、角边角和边边边定理,直角三角形全等还有斜边直角边定理,逐项分析即可判断.
5. B
考点:直角三角形全等的判定
解:∵AB为公共边,也为 Rt△ABC和Rt△ABD的斜边,
∴ 若要用“HL”证明Rt△ABC≌Rt△ABD,则还需要一组直角边对应相等,
即 AC=AD或BC=BD?;
故答案为:B.
分析: 用“HL”证明两个直角三角形全等,需要证明斜边和一组直角边对应相等。现知斜边相等,则只需一组直角边对应相等,据此分析判断即可。
6. B
考点:直角三角形全等的判定
解:∵AC=BC,AE=CD,
∴△AEC≌△CDB(HL),
∴CD=AE=7,CE=BD=2,
∴ED=CD-CE=7-2=5,
故答案为:B.
分析:根据斜边直角边定理证明△AEC≌△CDB,再由全等三角形的性质定理得对应边相等,则CD和CE的长度可求,于是求出ED的长度。
7. D
考点:直角三角形全等的判定
解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故答案为:D.
分析:这个题目考查的是直角三角形的判定定理的运用。前提条件必须是两个直角三角形,必须有斜边,再加一条直角边,用两个条件即可证明全等。特别注意证明过程的格式书写。
8. A
考点:直角三角形全等的判定
解:在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故答案为:A.
分析:由作图可知OM=ON ,∠OMP=∠ONP再根据OP是公共边即可作出判断.
9. A
考点:直角三角形全等的判定
解:∵四边形ABCD是正方形,
∴∠EDB=∠OBF,DO=BO,
在△EDO和△FBO中,
∴△DEO≌△BFO(ASA),
∴S△DEO=S△BFO,
阴影面积 ?
故答案为:A
分析:在正方形ABCD中,根据三角形的的两个角及其夹边对应相等,两个三角形全等,可证△DEO≌△BFO(ASA),所以阴影部分的面积可以转化为正方形面积的即可。
10.A
考点:直角三角形全等的判定
解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,
∴EB=EF,
又∵AE=AE
∴Rt△AEF≌Rt△AEB
∴AB=AF,∠AEF=∠AEB;
而点E是BC的中点,
∴EC=EF=BE,所以③错误;
∴Rt△EFD≌Rt△ECD,
∴DC=DF,∠FDE=∠CDE,所以②正确;
∴AD=AF+FD=AB+DC,所以④正确;
∴∠AED=∠AEF+∠FED= ∠BEC=90°,所以①正确.
故答案为:A
分析:过E作EF⊥AD于F,如图,根据角平分线上的点到角两边的距离相等得出EB=EF,然后利用HL判断出Rt△AEF≌Rt△AEB,根据全等三角形的对应角相等,对应边相等得出AB=AF,∠AEF=∠AEB;根据中点的定义从而得出EC=EF=BE;然后利用HL判断出Rt△EFD≌Rt△ECD,根据全等三角形的对应角相等,对应边相等得出DC=DF,∠FDE=∠CDE,然后根据线段的和差及等量代换,由AD=AF+FD=AB+DC得出AD=AB+CD,根据平角的定义及角的和差得出∠AED=∠AEF+∠FED=?∠BEC=90°。
二、填空题
11.△DFE;HL
考点:直角三角形全等的判定
解:EB+BF=FC+BF,即EF=BC,斜边相等分析:根据等式的性质由EB=FC得出EF=BC,这两个直角三角形中有一条直角边对应相等,斜边也对应相等,故可以利用HL判断出ΔABC≌△DFE。
12. 5或10
考点:直角三角形全等的判定
解:当AP=5或10时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=5=BC时,
在Rt△ACB和Rt△QAP中
,
∴Rt△ACB≌Rt△QAP(HL),
②当AP=10=AC时,
在Rt△ACB和Rt△PAQ中
,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:5或10.
分析:根据直角三角形全等的判定定理,分别证明三角形全等,即可得到答案。
13. 12
考点:直角三角形全等的判定
解:连接BE,
∵D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,
∴∠A=∠BDE=90°,
∴在Rt△DBE和Rt△ABE中,
BD=AB(已知),BE=EB(公共边),
∴Rt△DBE≌Rt△ABE(HL),
∴AE=ED,
又∵AE=12cm,
∴ED=12cm.
故填12.
分析:根据直角三角形全等的判定定理容易证得Rt△DBE≌Rt△ABE(HL),从而可以得出结论
14. 8
考点:全等三角形的性质,直角三角形全等的判定(HL),角平分线的性质
解:∵∠C=90?,BD平分∠CBA,DE⊥AB,
∴CD=DE,
在Rt△BCD和Rt△BED中,
∵
∴Rt△BCD≌Rt△BED(HL),
∴BC=BE,
∴△ADE的周长=AE+AD+DE=AE+AD+CD=AE+AC=AE+BC=AE+BE=AB,
∵△ADE的周长为8cm,
∴AB=8cm.
故答案为:8cm.
分析:根据题意,结合角平分线的性质,即可得到CD=DE,在题目中,结合已知条件证明直角三角形BCD≌直角三角形BED,即可根据全等三角形的性质得到BC=BE,将△ADE的周长转化为三角形ACB中已知边的长度求出答案即可。
15.
考点:三角形的外角性质,直角三角形全等的判定,角平分线的性质
解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD?∠BPC=(x?40)°,
∴∠BAC=∠ACD?∠ABC=2x°?(x°?40°)?(x°?40°)=80°,
∴∠CAF=100°,
在Rt△PFA和Rt△PMA中,
PA=PA
PM=PF,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=50°.
分析: 根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP,即可得出答案.
三、解答题
16. 证明:∵AC⊥AB于点A,BD⊥AB于点B,
∴∠A=∠B=90°,
∵AF=BE,
∴AE=BF,
∵CE=DF,
∴Rt△ACE≌Rt△BDF(HL),
∴∠C=∠D.
考点:直角三角形全等的判定
分析:先根据等量加等量和相等得出 AE=BF, 然后利用“HL”判断Rt△ACE≌Rt△BDF,由全等三角形的对应角相等可得 ∠C=∠D.
17. 证明:∵AB∥DC
∴∠ACD=∠BAC
∵AE⊥BC
∴∠AEC=90°
在Rt△ACE和Rt△ACD中
∴Rt△ACE≌Rt△ACD(HL)
∴∠ACB=∠ACD.
∴∠ACB=∠BAC.
考点:直角三角形全等的判定
分析:根据直角三角形的判定定理(HL)可判断出三角形全等,根据全等三角形的性质可得出对应角相等。
18. (1)Rt△ADE与Rt△BEC全等 ,
证明:∵ ∠A=∠B=90 °,
AE=BC,
∵∠1=∠2 ,
则DE=CE,
∴ Rt△ADE≌Rt△BEC(HL);
(2)证明,∵Rt△ADE≌Rt△BEC,
则AD=BE,AE=BC,
∴AE+EB=AD+BC,
即AB=AD+BC.
(3)解:∵Rt△ADE≌Rt△BEC,
∴ ∠AED=∠BCE,
∵ ∠AED+∠BEC=?∠BCE+∠BEC=90°,
∴∠DEC=90°.
考点:直角三角形全等的判定
分析:(1)利用斜边直角边定理,证明两三角形全等即可;
(2)由全等三角形对应边分别相等,结合等式的性质,即可证得AB=AD+BC;
(3)由全等三角形对应角相等,结合等式的性质,求得∠AED和∠BEC之和等于90°,则∠DEC等于90°。
19. (1)证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°
∴△ABF与ADCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF=Rt△DCE(HL),
∴AF=DE
(2)证明:∵Rt△ABF=Rt△DCE(已证),
∴∠AFB=∠DEC,
∴OE=OF,
∵OP⊥FE
∴OP平分∠EOF
考点:直角三角形全等的判定
分析:(1)由BE=CF,可得到BF=CE,在Rt △ABF与Rt△ADC中,利用“HL”定理即可证得Rt△ABF=Rt△DCE,可得AF=DE;
(2)由(1)中结论可判断∠AFB=∠DEC,△OEF是等腰三角形,根据“三线合一”即可判断OP平分∠EOF。
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册2.8 直角三角形全等的判定 同步练习
一、单选题
1.下列判定直角三角形全等的方法,不正确的是(??? )
A.?两条直角边对应相等。???????????????????????????????????????B.?斜边和一锐角对应相等。
C.?斜边和一条直角边对应相等。?????????????????????????????D.?两锐角相等。
2.如图,AC,BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.下列条件不能保证两个三角形全等的是(???? )
A.?三边对应相等??????????????????????????????????????????????????B.?两边一角对应相等
C.?两角一边对应相等???????????????????????????????????????????D.?直角边和一个锐角对应相等
4.如图△ABC和△DEF,下列条件中①∠B=∠E=90°,AC=DF;②∠B=∠E,AB=DE,AC=DF;③在Rt△ABC和Rt△DEF中,BC=EF,AC=DF;④∠A=∠D,∠B=∠E,∠C=∠F;⑤∠A=∠D,BC=EF,∠C=∠F,能证明△ABC≌△DEF的是(?? )
A.?③ ⑤????????????????????????????B.?① ③⑤????????????????????????????C.?①② ③⑤????????????????????????????D.?①② ③④⑤
5.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件(??? )
A.?∠BAC=∠BAD???????????B.?AC=AD或BC=BD???????????C.?AC=AD且BC=BD???????????D.?以上都不正确
6.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( ??)
A.?7???????????????????????????????????????????B.?5???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
7.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是(?? )
A.?AE=DF?????????????????????????????B.?∠A=∠D?????????????????????????????C.?∠B=∠C?????????????????????????????D.?AB=DC
8.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是(?? )
A.?HL??????????????????????????????????????B.?SAS??????????????????????????????????????C.?AAS??????????????????????????????????????D.?SSS
9.如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC于E、F两点,则阴影部分的面积是(? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
10.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE;④AD=AB+CD,四个结论中成立的是(? ??)
A.?①②④???????????????????????????B.?①②③?????????????????????????????????C.?②③④?????????????????????????????????D.?①③
二、填空题
11.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌________,全等的根据是________.
12.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB , P , Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=________时,△ABC和△PQA全等.
13.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 ________?cm.
14.如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D , DE⊥AB于E . 若△ADE的周长为8cm , 则AB=________ cm .
15.如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=________.
三、解答题
16.如图,已知AC⊥AB于点A,BD⊥AB于点B,AF=BE,CE=DF,求证:∠C=∠D.
17.已知DC=EC,AB∥DC,∠D=90°, AE⊥BC于点E.求证:∠ACB=∠BAC.
18.如图,四边形ABCD中,∠A=∠B=90度,E是AB上一点,且AE=BC,∠1=∠2
(1)Rt△ADE与Rt△BEC全等吗?请说明理由;
(2)AB=AD+BC
(3)△CDE是不是直角三角形?请说明理由.
19.如图所示∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
(1)求证:AF=DE.
(2)若PO⊥EF,求证:OP平分∠EOF.
答案解析部分
一、单选题
1. D
考点:直角三角形全等的判定
解:如果在两个直角三角形中,两条直角边对应相等,那么根据SAS即可判断两三角形全等,故答案为:A正确.
如果在两个直角三角形中,斜边和一锐角对应相等,那么根据AAS也可判断两三角形全等,故答案为:B正确.
如果在两个直角三角形中,斜边和一直角边对应相等,那么根据HL也可判断两三角形全等,故答案为:C正确.
如果在两个直角三角形中,两锐角相等,无法判断两三角形全等,故答案为:D错误.
故答案为:D.
分析:根据直角三角形全等的判定方法:SSS,SAS,ASA,AAS,HL即可一一判断得出答案.
2. D
考点:直角三角形全等的判定
解:根据矩形的性质,△CDA、△BAD、△DCB与△ABC全等,因为DE∥AC,所以∠CDE=∠DCA,因为CD=DC,∠ADC=∠ECD,所以△ADC≌△ECD,所以与△ABC全等的三角形有4个.
故答案为:D.
分析:根据题中条件,结合图形,可得出与△ABC全等的三角形为△ADC,△ABD,△DBC,△DCE共4个.
3. B
考点:直角三角形全等的判定
解:A、 三边对应相等 (SSS),则三角形全等,正确,不符合题意;
B、 两边一角对应相等?,无边边角定理,不能证明三角形全等,错误,不符合题意;
C、 两角一边对应相等(AAS),则三角形全等,正确,不符合题意;
D、 直角边和一个锐角对应相等 (ASA),则三角形全等,正确,不符合题意.
故答案为:B.
分析:三角形全等的判定定理有:边角边、角角边、角边角和边边边定理,逐项分析即可判断.
4. A
考点:直角三角形全等的判定
解:??①∠B=∠E=90°,AC=DF,只有两个要素对应相等不能证明三角形全等,不符合题意;
②∠B=∠E,AB=DE, AC=DF,无边边角定理,不能证明两三角形全等,不符合题意 ;
③在Rt△ABC和Rt△DEF中,BC=EF,AC=DF,则 △ABC≌△DEF (HL),符合题意;
④∠A=∠D,∠B=∠E,∠C=∠F,三个角对应相等,不能证明两三角形全等,不符合题意;
⑤∠A=∠D,BC=EF,∠C=∠F,则 △ABC≌△DEF(AAS)?, 符合题意;
综上,只有 ③⑤ 符合题意.
故答案为:A.
?分析:三角形全等的判定定理有:边角边、角角边、角边角和边边边定理,直角三角形全等还有斜边直角边定理,逐项分析即可判断.
5. B
考点:直角三角形全等的判定
解:∵AB为公共边,也为 Rt△ABC和Rt△ABD的斜边,
∴ 若要用“HL”证明Rt△ABC≌Rt△ABD,则还需要一组直角边对应相等,
即 AC=AD或BC=BD?;
故答案为:B.
分析: 用“HL”证明两个直角三角形全等,需要证明斜边和一组直角边对应相等。现知斜边相等,则只需一组直角边对应相等,据此分析判断即可。
6. B
考点:直角三角形全等的判定
解:∵AC=BC,AE=CD,
∴△AEC≌△CDB(HL),
∴CD=AE=7,CE=BD=2,
∴ED=CD-CE=7-2=5,
故答案为:B.
分析:根据斜边直角边定理证明△AEC≌△CDB,再由全等三角形的性质定理得对应边相等,则CD和CE的长度可求,于是求出ED的长度。
7. D
考点:直角三角形全等的判定
解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故答案为:D.
分析:这个题目考查的是直角三角形的判定定理的运用。前提条件必须是两个直角三角形,必须有斜边,再加一条直角边,用两个条件即可证明全等。特别注意证明过程的格式书写。
8. A
考点:直角三角形全等的判定
解:在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故答案为:A.
分析:由作图可知OM=ON ,∠OMP=∠ONP再根据OP是公共边即可作出判断.
9. A
考点:直角三角形全等的判定
解:∵四边形ABCD是正方形,
∴∠EDB=∠OBF,DO=BO,
在△EDO和△FBO中,
∴△DEO≌△BFO(ASA),
∴S△DEO=S△BFO,
阴影面积 ?
故答案为:A
分析:在正方形ABCD中,根据三角形的的两个角及其夹边对应相等,两个三角形全等,可证△DEO≌△BFO(ASA),所以阴影部分的面积可以转化为正方形面积的即可。
10.A
考点:直角三角形全等的判定
解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,
∴EB=EF,
又∵AE=AE
∴Rt△AEF≌Rt△AEB
∴AB=AF,∠AEF=∠AEB;
而点E是BC的中点,
∴EC=EF=BE,所以③错误;
∴Rt△EFD≌Rt△ECD,
∴DC=DF,∠FDE=∠CDE,所以②正确;
∴AD=AF+FD=AB+DC,所以④正确;
∴∠AED=∠AEF+∠FED= ∠BEC=90°,所以①正确.
故答案为:A
分析:过E作EF⊥AD于F,如图,根据角平分线上的点到角两边的距离相等得出EB=EF,然后利用HL判断出Rt△AEF≌Rt△AEB,根据全等三角形的对应角相等,对应边相等得出AB=AF,∠AEF=∠AEB;根据中点的定义从而得出EC=EF=BE;然后利用HL判断出Rt△EFD≌Rt△ECD,根据全等三角形的对应角相等,对应边相等得出DC=DF,∠FDE=∠CDE,然后根据线段的和差及等量代换,由AD=AF+FD=AB+DC得出AD=AB+CD,根据平角的定义及角的和差得出∠AED=∠AEF+∠FED=?∠BEC=90°。
二、填空题
11.△DFE;HL
考点:直角三角形全等的判定
解:EB+BF=FC+BF,即EF=BC,斜边相等分析:根据等式的性质由EB=FC得出EF=BC,这两个直角三角形中有一条直角边对应相等,斜边也对应相等,故可以利用HL判断出ΔABC≌△DFE。
12. 5或10
考点:直角三角形全等的判定
解:当AP=5或10时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=5=BC时,
在Rt△ACB和Rt△QAP中
,
∴Rt△ACB≌Rt△QAP(HL),
②当AP=10=AC时,
在Rt△ACB和Rt△PAQ中
,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:5或10.
分析:根据直角三角形全等的判定定理,分别证明三角形全等,即可得到答案。
13. 12
考点:直角三角形全等的判定
解:连接BE,
∵D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,
∴∠A=∠BDE=90°,
∴在Rt△DBE和Rt△ABE中,
BD=AB(已知),BE=EB(公共边),
∴Rt△DBE≌Rt△ABE(HL),
∴AE=ED,
又∵AE=12cm,
∴ED=12cm.
故填12.
分析:根据直角三角形全等的判定定理容易证得Rt△DBE≌Rt△ABE(HL),从而可以得出结论
14. 8
考点:全等三角形的性质,直角三角形全等的判定(HL),角平分线的性质
解:∵∠C=90?,BD平分∠CBA,DE⊥AB,
∴CD=DE,
在Rt△BCD和Rt△BED中,
∵
∴Rt△BCD≌Rt△BED(HL),
∴BC=BE,
∴△ADE的周长=AE+AD+DE=AE+AD+CD=AE+AC=AE+BC=AE+BE=AB,
∵△ADE的周长为8cm,
∴AB=8cm.
故答案为:8cm.
分析:根据题意,结合角平分线的性质,即可得到CD=DE,在题目中,结合已知条件证明直角三角形BCD≌直角三角形BED,即可根据全等三角形的性质得到BC=BE,将△ADE的周长转化为三角形ACB中已知边的长度求出答案即可。
15.
考点:三角形的外角性质,直角三角形全等的判定,角平分线的性质
解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD?∠BPC=(x?40)°,
∴∠BAC=∠ACD?∠ABC=2x°?(x°?40°)?(x°?40°)=80°,
∴∠CAF=100°,
在Rt△PFA和Rt△PMA中,
PA=PA
PM=PF,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=50°.
分析: 根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP,即可得出答案.
三、解答题
16. 证明:∵AC⊥AB于点A,BD⊥AB于点B,
∴∠A=∠B=90°,
∵AF=BE,
∴AE=BF,
∵CE=DF,
∴Rt△ACE≌Rt△BDF(HL),
∴∠C=∠D.
考点:直角三角形全等的判定
分析:先根据等量加等量和相等得出 AE=BF, 然后利用“HL”判断Rt△ACE≌Rt△BDF,由全等三角形的对应角相等可得 ∠C=∠D.
17. 证明:∵AB∥DC
∴∠ACD=∠BAC
∵AE⊥BC
∴∠AEC=90°
在Rt△ACE和Rt△ACD中
∴Rt△ACE≌Rt△ACD(HL)
∴∠ACB=∠ACD.
∴∠ACB=∠BAC.
考点:直角三角形全等的判定
分析:根据直角三角形的判定定理(HL)可判断出三角形全等,根据全等三角形的性质可得出对应角相等。
18. (1)Rt△ADE与Rt△BEC全等 ,
证明:∵ ∠A=∠B=90 °,
AE=BC,
∵∠1=∠2 ,
则DE=CE,
∴ Rt△ADE≌Rt△BEC(HL);
(2)证明,∵Rt△ADE≌Rt△BEC,
则AD=BE,AE=BC,
∴AE+EB=AD+BC,
即AB=AD+BC.
(3)解:∵Rt△ADE≌Rt△BEC,
∴ ∠AED=∠BCE,
∵ ∠AED+∠BEC=?∠BCE+∠BEC=90°,
∴∠DEC=90°.
考点:直角三角形全等的判定
分析:(1)利用斜边直角边定理,证明两三角形全等即可;
(2)由全等三角形对应边分别相等,结合等式的性质,即可证得AB=AD+BC;
(3)由全等三角形对应角相等,结合等式的性质,求得∠AED和∠BEC之和等于90°,则∠DEC等于90°。
19. (1)证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°
∴△ABF与ADCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF=Rt△DCE(HL),
∴AF=DE
(2)证明:∵Rt△ABF=Rt△DCE(已证),
∴∠AFB=∠DEC,
∴OE=OF,
∵OP⊥FE
∴OP平分∠EOF
考点:直角三角形全等的判定
分析:(1)由BE=CF,可得到BF=CE,在Rt △ABF与Rt△ADC中,利用“HL”定理即可证得Rt△ABF=Rt△DCE,可得AF=DE;
(2)由(1)中结论可判断∠AFB=∠DEC,△OEF是等腰三角形,根据“三线合一”即可判断OP平分∠EOF。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
