2.6.1 直角三角形同步练习(含解析）

中小学教育资源及组卷应用平台
初中数学浙教版八年级上册2.6 直角三角形（1）同步练习
一、单选题
1.如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3 cm，则AB的长度是(?? )
A.?3cm????????????????????????????????????B.?6cm????????????????????????????????????C.?9cm????????????????????????????????????D.?12cm
2.如图，在△ABC中，∠ACB=90°，CD是AB边上的高线，图中与∠A互余的角有（?? ）
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
3.如图，一根竹竿AB，斜靠在竖直的墙上，P是AB中点，A'B'表示竹竿AB端沿墙上、下滑动过程中的某个位置，则在竹竿AB滑动过程中OP(??? )

A.?下滑时，OP增大?????? B.?上升时，OP减小??????
C.?无论怎样滑动，OP不变?????? D.?只要滑动，OP就变化
4.如图所示，已知∠1=∠2，AD=BD=4，CE⊥AD，2CE=AC，那么CD的长是（??? ）
A.?2??????????????????????????????????????????B.?3??????????????????????????????????????????C.?1??????????????????????????????????????????D.?1.5
5.如果一个三角形的三边长分别为 3、4、5 ，那么它的斜边上的高为（? ??）
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
6.如图，Rt△ACB中，∠ACB=90°，∠A=60°，CD，CE分别是△ABC的高和中线，下列说法错误的是(??? )

A.?AD=DE???????????????????????????????????????????????????????????? B.?S△CEB=S△ACE
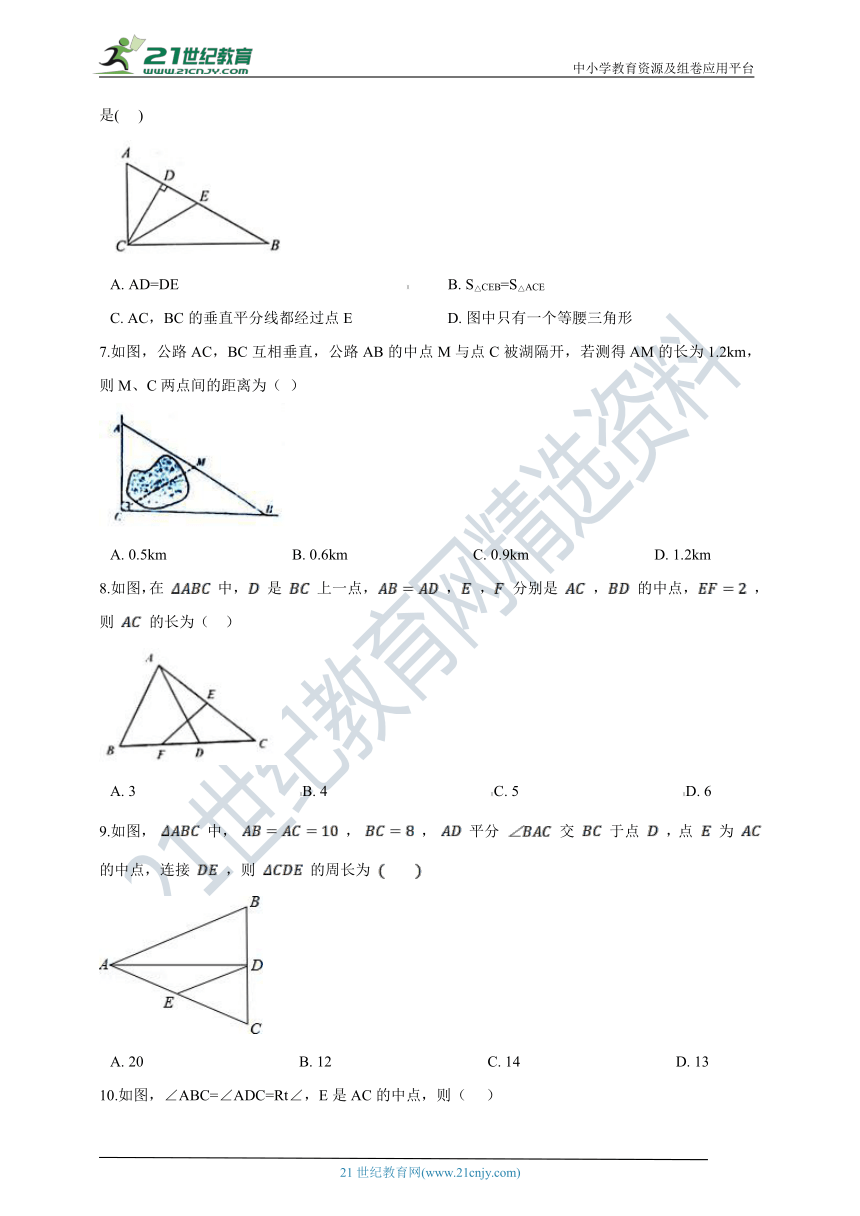
C.?AC，BC的垂直平分线都经过点E?????????????????????????D.?图中只有一个等腰三角形
7.如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AM的长为1.2km，则M、C两点间的距离为（ ）
A.?0.5km?????????????????????????????????B.?0.6km?????????????????????????????????C.?0.9km?????????????????????????????????D.?1.2km
8.如图，在 中， 是 上一点， ， ， 分别是 ， 的中点， ，则 的长为（?? ）
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
9.如图， 中， ， ， 平分 交 于点 ，点 为 的中点，连接 ，则 的周长为 ??
A.?20?????????????????????????????????????????B.?12?????????????????????????????????????????C.?14?????????????????????????????????????????D.?13
10.如图，∠ABC=∠ADC=Rt∠，E是AC的中点，则（??? ）
A.?∠1＞∠2????????????????????B.?∠1=∠2????????????????????C.?∠1＜∠2????????????????????D.?∠1与∠2大小关系不能确定
二、填空题
11.如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD平分∠ABC，P点是BD的中点，若AD=10，则CP的长为________.
12.在Rt ABC中，∠C=90°，∠A=65°，则∠B=________.
13.如图，已知AB是Rt△ABC和Rt△ABD的斜边，O是AB的中点，其中OC是2 cm，则OD＝________.
14.如图：在 中，CD是斜边AB上的中线，若 ，则 ________．
15.如图，已知在 中， ，点D在边 上，且 ， .则 的度数为________°．
三、解答题
16.已知：如图， ， 分别是 、 的中点. 求证： .
17.已知：如图，在△ABC中，D是BC上的点，AD=AB，E，F分别是AC，BD的中点，AC=6．求EF的长。

18.如图，在△ABC中，∠B＝2∠C，AE平分∠BAC交BC于点E.
（1）如图①，若AD⊥BC于点D，∠C＝40°，求∠DAE的度数；
（2）如图②，若EF⊥AE交AC于点F，求证：∠C＝2∠FEC.
19.已知：如图∠ABC=∠ADC=90°，M，N分别是AC、BD的中点.
（1）试判断△BMD的形状，并说明理由.
（2）求证： MN⊥BD.
20.如图，在△ABC中，AD是△ABC的高线，CE是△ABC的角平分线，它们相交于点P．
（1）若∠B＝40°，∠AEC＝75°，求证：AB＝BC；
（2）若∠BAC＝90°，AP为△AEC边EC上中线，求∠B的度数．
答案解析部分
一、单选题
1. D
考点：含30度角的直角三角形，直角三角形的性质
解：在Rt△ABC中，∵CD是斜边AB上的高，∴∠ADC=90°，
∴∠ACD+∠DCB=90°，∠B+∠DCB=90°，
∴∠ACD=∠B=30°.
∵AD=3cm.
在Rt△ACD中，AC=2AD=6cm，
在Rt△ABC中，AB=2AC=12cm，
∴AB的长度是12cm.
故答案为：D.
分析：根据直角三角形的两锐角互余及同角的余角相等得出∠ACD=∠B=30°，进而根据含30°直角三角形的边之间的关系即可得出AB=2AC=2AD=12cm.
2. C
考点：直角三角形的性质
解：∵∠ACB=90°，CD是AB边上的高线，
∴∠A+∠B=90°，∠A+∠ACD=90°，
∴与∠A互余的角有2个，
故答案为：C.
分析：根据和为90度的两个角互为余角并结合已知条件可判断求解.
3. C
考点：直角三角形斜边上的中线
解：∵AO⊥BO，点P为AB的中点
∴OP=AB
∴在滑动的过程中，OP的长度不变
故答案为：C.
分析：根据直角三角形斜边上的中线等于斜边的一半，即可得到OP的长度。
4. A
考点：三角形内角和定理，含30度角的直角三角形
解：在Rt△AEC中，∵ = ，∴∠1=∠2=30°，
∵AD=BD=4，∴∠B=∠2=30°，∴∠ACD=180°﹣30°×3=90°，∴CD= AD=2.
故答案为：A.
分析：在Rt△AEC中，由于 = ，可以得到∠1=∠2=30°，又AD=BD=4，得到∠B=∠2=30°，从而求出∠ACD=90°，然后由直角三角形的性质求出CD.
5. A
考点：三角形的面积，直角三角形的性质
解：∵
∴斜边是5，
设斜边上的高是h，根据直角三角形的面积可得：
，
解得： ．
故答案为：A．
分析：在一个直角三角形中，斜边最长，即斜边是5，设斜边上的高是h，根据面积公式即可求得高的长．
6. D
考点：三角形的面积，直角三角形的性质
解：A.∵CE为直角三角形ABC的斜边上的中线，∴CE=AE=EB
在△ACE中，∵∠A=60°，∴△ACE为等边三角形
又∵CD⊥AE
∴AD=DE，选项正确。
B.∵AE=EB，△ACE和△CEB有共同的高CD，
∴S△ACE=S△CEB，选项正确。
C.在等边三角形ACE中，AC边上的垂直平分线经过点E，在等腰三角形CEB中，BC边上的垂直平分线经过点E，选项正确。
D.图中存在两个等腰三角形，△ACE和△CEB，选项错误。
故答案为：D.
分析：根据直角三角形的性质，结合等腰三角形的性质进行判断即可。
7. D
考点：直角三角形斜边上的中线
解：根据直角三角形斜边上的中线等于斜边的一半即可求得距离为1.2km.
故答案为：D
分析：直角三角形斜边上的中线等于斜边的一半。
8. B
考点：等腰三角形的性质，直角三角形斜边上的中线
解：如图，连结AF．
∵AB=AD，F是BD的中点，
∴AF⊥BD．
又∵在Rt△ACF中，∠AFC=90°，E是AC的中点，EF=2，
∴AC=2EF=4．
故选：B．
分析：连结AF．由AB=AD，F是BD的中点，根据等腰三角形三线合一的性质得出AF⊥BD．再根据直角三角形斜边上的中线等于斜边的一半求得AC=2EF=4．
9. C
考点：等腰三角形的性质，直角三角形的性质
解： ， 平分 ， ，
， ，
点 为 的中点，
，
的周长 ．
故选：
分析：根据等腰三角形三线合一的性质可得 ， ，再根据直角三角形斜边上的中线等于斜边的一半可得 ，然后根据三角形的周长公式列式计算即可得解.
10. B
考点：等腰三角形的性质，直角三角形斜边上的中线
解：∵∠ABC=∠ADC=90°，E是AC的中点，
∴DE= AC，BE= AC，
∴DE=BE，
∴∠1=∠2．
故答案为：B．
分析：根据直角三角形斜边上的中线等于斜边的一半，可以证明DE=BE，再根据等腰三角形的性质即可解答．
二、填空题
11. 5
考点：三角形内角和定理，等腰三角形的性质，直角三角形斜边上的中线
解：∵在△ABC中，∠ACB=90°，∠ABC=60°，
∴∠A=30°，
∵BD平分∠ABC，
∴∠ABD=∠A=30°，
∴BD=AD=10，
∵点P是BD中点，∠ACB=90°，
∴CP= BD=5，
故答案为：5.
分析：根据三角形的内角和定理及角平分线的定义算出∠ABD=∠A=30°，然后根据等角对等边得出BD=AD=10，进而根据直角三角形斜边上的中线等于斜边的一半即可算出答案.
12. 25°
考点：直角三角形的性质
解：如图，在直角三角形ABC中，∠C=90°，∠A=65°，
则∠B=90°-∠A=25°（直角三角形中，两个锐角互余）.
故答案是：25°.
分析：根据直角三角形中，两个锐角互余即可算出∠B的度数.
13. 2cm
考点：直角三角形斜边上的中线
解：∵AB是Rt△ABC和Rt△ABD的斜边，O是AB的中点，∴OC=OD.
∵OC=2cm，∴OD=2cm.
故答案为：2cm.
分析：根据直角三角形斜边上的中线等于斜边的一半得出OC=OD=AB，从而即可得出答案.
14. 40°
考点：三角形的外角性质，等腰三角形的性质，直角三角形斜边上的中线
解：∵在 中，CD是斜边AB上的中线，，
∴ ．
∵ ，
∴ ，
∴ ．
故答案为：40°
分析：先根据直角三角形斜边中线的性质得出 ，则有 ，最后利用三角形外角的性质即可得出答案．
15. 105
考点：三角形内角和定理，三角形的外角性质，等腰三角形的性质，直角三角形斜边上的中线
解：取线段CD的中点E，连接AE，
∵∠DAC=90°，
∴AE=EC=DE= DC，（直角三角形斜边上的中线等于斜边的一半），
∴∠EAC=∠C，
∵∠C=25°，
∴∠AEB=∠EAC+∠C=50°，
∵AB= DC，
∴AB=AE（等量代换），
∴∠B=∠AEB=50°，
∵∠B+∠C+∠BAC=180°，
即50°+25°+∠BAC=180°，
∴∠BAC=105°．
故答案为：105.
分析：取线段CD的中点E，连接AE，根据直角三角形斜边上的中线等于斜边的一半可得AE=EC=DE= DC，再根据等边对等角的性质可得∠EAC=∠C，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEB，再求出AB=AE，根据等边对等角的性质求出∠B=∠AEB，然后利用三角形的内角和等于180°列式进行计算即可得解．
三、解答题
16. 证明：如图，连接BE、DE，
∵∠ABC=∠ADC=90°，E是AC的中点，
∴BE=DE= AC，
∵F是BD的中点，
∴EF⊥BD
考点：等腰三角形的性质，直角三角形斜边上的中线
分析： 如图，连接BE、DE， 根据直角三角形斜边上的中线等于斜边上的一半得出 BE=DE= AC， 进而根据等腰三角形的三线合一得出EF⊥BD .
17. 解：连结AF，
∵AB=AD，F是BD的中点，∴AF⊥BD，
又∵E是AC的中点， ∴EF= AC，∵AC=6，∴EF=3．
考点：等腰三角形的性质，直角三角形斜边上的中线
分析：根据等腰三角形的三线合一定理得出AF⊥BD，然后利用直角三角形斜边上的中线等于斜边的一半即可求出EF的长度.
18. （1）解：(1) ∵ ,
∴ , ,
?∴
?∴
（2）解：∵ ∴
∵AE平分∠BAC
∴ ,
∵ EF⊥AE,
∴
∴
?即：∠C＝2∠FEC
考点：三角形内角和定理，直角三角形的性质
分析：(1)首先计算出 的度数，可得出 ，再根据直角三角形两锐角互余得出 的度数，从而得到答案；(2)通过已知条件找出 ，进一步得出 ，从而得出结论.
19. （1）解：△BDM是等腰三角形，理由如下：
∵∠ABC=∠ADC=90°，M是AC的中点，
∴BM= AC，DM= AC，
∴BM=DM
∴△BDM是等腰三角形
（2）解：由（1）得BM=DM，
∵N为BD的中点，
∴MN⊥BD（三线合一）.
考点：等腰三角形的判定与性质，直角三角形斜边上的中线
分析：（1）由题知∠ABC=∠ADC=90°，M是AC的中点，则根据直角三角形中斜边上的中线等于斜边的一半，则BM= AC，DM= AC即可判断；（2）N为BD的中点，再由（1）知BM=DM，根据三线合一即可证明.
20. （1）证明：∵∠B＝40°，∠AEC＝75°，
∴∠∠ECB＝∠AEC﹣∠B＝35°，
∵CE平分∠ACB，
∴∠ACB＝2∠BCE＝70°，
∠BAC＝180°﹣∠B﹣∠ACB＝180°﹣40°﹣70°＝70°，
∴∠BAC＝∠BCA，
∴AB＝AC．
（2）解：∵∠BAC＝90°，AP是△AEC边EC上的中线，
∴AP＝PC，
∴∠PAC＝∠PCA，
∵CE是∠ACB的平分线，
∴ ∠PAC=∠PCA=∠ECD ，
∵∠ADC＝90°，
∴∠PAC＝∠PCA＝∠PCD＝90°÷3＝30°，
∴∠BAD＝60°，
∵∠ADB＝90°，
∴∠B＝90°﹣60°＝30°
考点：等腰三角形的性质，直角三角形斜边上的中线
分析：（1）利用∠B和∠AEC的度数求出∠ECB的度数，利用角平分线的定义求出∠ACB的度数；再利用三角形内角和定理求出∠BAC的值，从而可以推出∠BAC=∠BCA，然后利用等角对等边，可证得结论。
（2）利用直角三角形斜边上的中线等于斜边的一半，易证AP=PC，利用等边对等角，可推出∠PAC=∠PCA，结合角平分线的定义可得到∠PAC＝∠PCA＝∠ECD，利用直角三角形的两锐角互余，求出∠PAC的度数，由此可求出∠BAD的度数，然后求出∠B的度数。
_21?????????è?????(www.21cnjy.com)_