7.3 线段的长短比较（2）

(共24张PPT)
A
B
C
D
哦，好美味呀！
关注生活
小狗和小猫为什么选择直的路，是巧合吗？
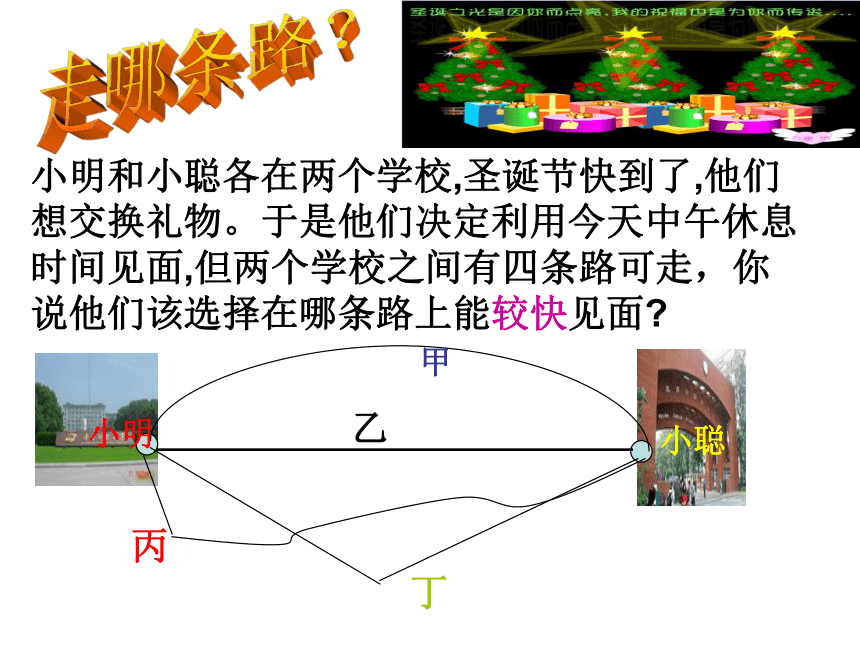
小明和小聪各在两个学校,圣诞节快到了,他们想交换礼物。于是他们决定利用今天中午休息时间见面,但两个学校之间有四条路可走，你说他们该选择在哪条路上能较快见面
小明
小聪
甲
乙
丁
丙
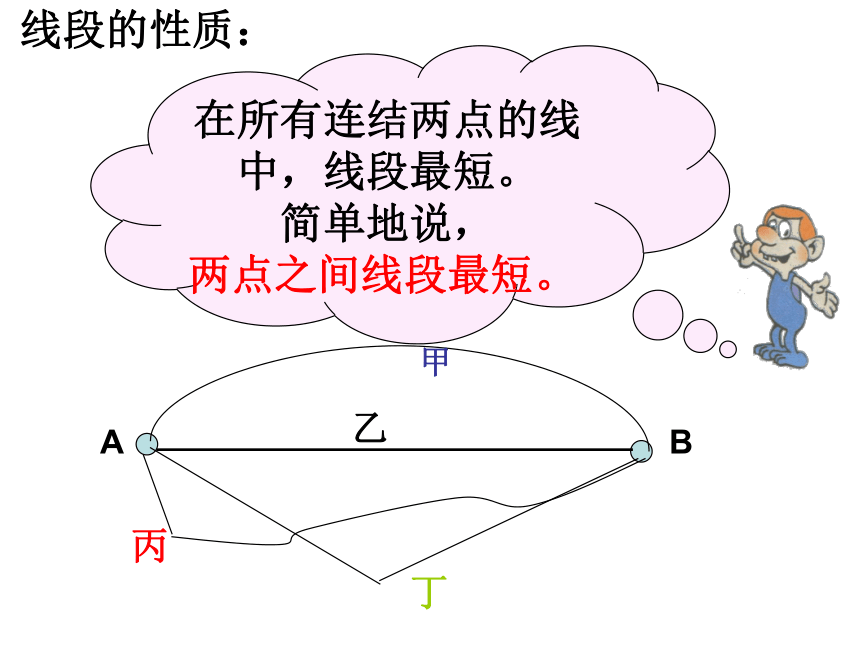
在所有连结两点的线中，线段最短。
简单地说，
两点之间线段最短。
线段的性质：
A
B
甲
乙
丁
丙
走进生活
你能举出利用“两点之间线段最短”的例子吗？
村庄A
村庄B
大桥P
河流
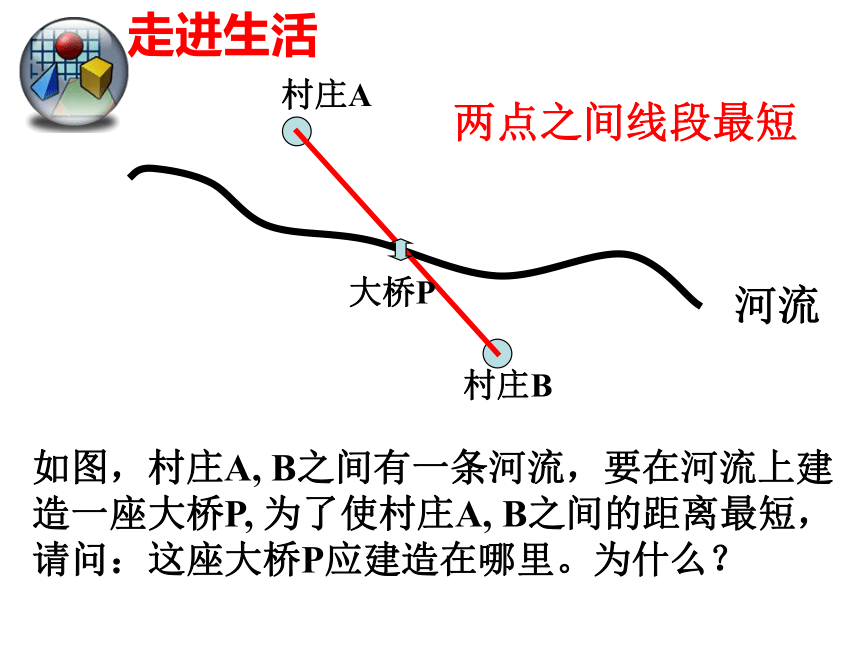
如图，村庄A, B之间有一条河流，要在河流上建造一座大桥P, 为了使村庄A, B之间的距离最短，请问：这座大桥P应建造在哪里。为什么？
两点之间线段最短
走进生活
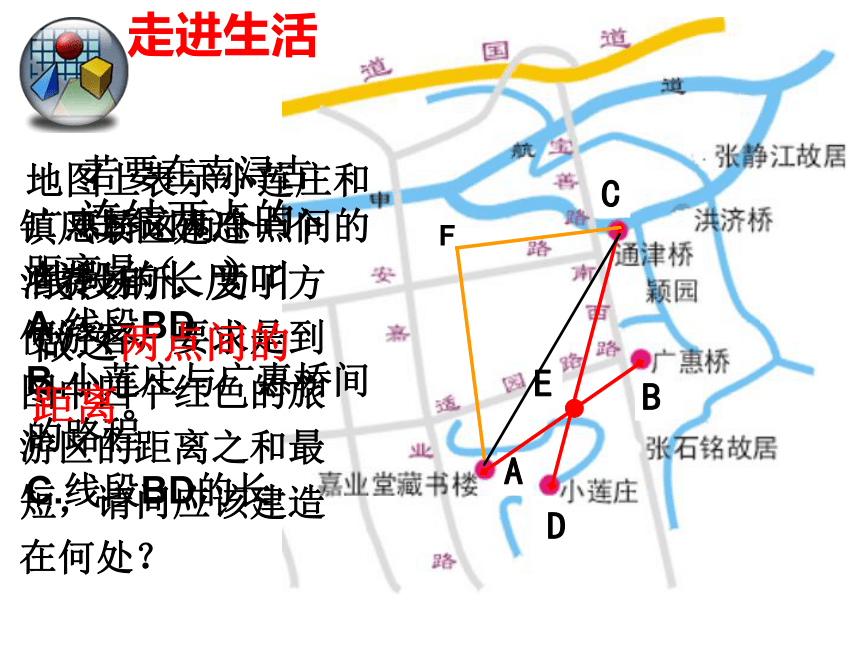
若要在南浔古镇风景区建造一个消费场所，为了方便游客，要求是到图中四个红色的旅游区的距离之和最短，请问应该建造在何处？
A
B
C
D
E
走进生活
F
地图上表示小莲庄和广惠桥这两个点间的距离是（ ）
A.线段BD
B.小莲庄与广惠桥间的路程
C.线段BD的长
连结两点的线段的长度叫做这两点间的距离。
小明和小聪他们都是讲公平有原则的人,希望见面的地点离各自学校的路程大致相等。他们该在何处见面
小明
小聪
O
任意画一条线段，你能画出它的中点吗？
点C把线段AB分成相等的两条线段AC 和BC，点C叫做线段AB的中点。
线段中点的定义：
A
B
C
A
B
C
若点C为线段AB的中点，则
AB=2AC=2BC
如上图,若AC=2cm,
则线段AB= cm,
线段BC= cm
（1）如果点P是AB的中点，则AP= _ _ AB
（2）如果点C，D三等分AB，则AC=CD= _ _ = _ _ AB
A
B
C
D
P
DB
（3）CP可以表示成哪两条线段的差？你有几种不同的表示？
1
2
1
3
例3、如图，点P是线段AB的中点，点C、D把线段AB三等分。已知线段CP的长为1.5cm，求线段AB的长？
A
B
A
D
C
P
如图，已知线段AB=a,延长BA至点C，使AC= AB。点D为线段BC的中点。
（1）求CD的长。
（2）若AD=3cm，求AB的长。
A
B
C
D
课堂小结：
这节课你学会了什么？
1.线段的基本性质：两点之间线段最短。
2.两点之间的距离：两点之间线段的长度。
3.线段的中点的概念。
作业：作业本(1)
探究：
A
P
如图，立方体纸盒P处粘有一粒糖，A处有一只蚂蚁沿着纸盒表面爬向糖粒。你能帮助蚂蚁找到一条最短的路线吗？请在图上画出这条最短路线，并说明理由。
P
A
两点之间线段最短
线段的基本性质：
A
P
作业友情提示
（1）作业本(1)第37页
（2）课本第173页作业题1---5
（3）预习：P173---177页
下课了！
合 作 学 习
请按下面的步骤操作：
1、在一张透明纸上画一条线段AB；
2、对折这张纸，使线段AB的两个
端点重合；
3、把纸展开铺平，标明折痕点C。
问：你能发现什么吗？
升级探究
已知线段AC=1，BC=3
则线段AB的长度是( )
A.4 B.2 C.2或4 D.非以上答案
D
做一做
1、如图，点C是线段AB的中点，
AC=8cm, 则BC= cm,
AB= cm.
A
B
C
8
16
2.已知线段AB的长度为2cm，延长线段AB至点C，
使BC＝AB.
A
B
C
A
B
则AC=
点B是线段AC的
4cm
中点
在这个图中，如何延长使点A成为线段的中点？
D
问题征答
下列说法正确的是(　　)
过A、B两点的直线长是A、B两点间的距离
B.线段AB就是A、B两点间的距离
C.乘火车从杭州到上海要走210千米，这就是说
　杭州站与上海站间的距离为210千米
D. 连结A、B两点的所有线中，其中最短的线的长度就是A、B两点间的距离
D
例3、如图，点P是线段AB的中点，点C、D把线段AB三等分。已知线段CP=1.5cm，求线段AB的长。
A
B
C
A
D
解：
∵ 点P是线段AB的中点，
∵ 点 C、D把线 段AB三等分，
∵ CP=AP －AC
即 AB的长是9cm
∴ AB=6PC
AB=6×1.5　　　
C
P
问：若要在西湖风景区建造一个消费场所，为了方便游客，要求是到图中四个红色的旅游区的距离之和最短，请问应该建造在何处？
A
B
C
D
E
F
如图，线段AB与线段CD的交点E为所求的点，即消费场所建在E点位置最合适。
解：
例3、如图，点P是线段AB的中点，点C、D把线段AB三等分。已知线段CP的长为1.5cm，求线段AB的长？
A
B
A
D
C
P