第2章 有理数的运算单元测试卷(含解析)
文档属性
| 名称 | 第2章 有理数的运算单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 321.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-01 20:09:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
七年级数学上册有理数的运算单元测试卷
(满分100分)
题号
一
二
三
四
总分
得分
一、选择题(本大题共10小题,共30.0分)
小明做了这样一道计算题:|(-3)+■|,其中“■”表示被墨水污染看不到的一个数,他分析了后边的答案得知该题的计算结果为16,那么“■”表示的数应该是(
)
A.
13
B.
-13
C.
19
D.
-13或19
在下列式子:①5×(-4)×(-2);②;③(-4)4;④(-3)5中.其中,计算结果是负数的有?
(???
)
①②
B.
①②③
C.
①③④
D.
②④
某市人口数约是305600人,这个数用科学记数法表示为(
)
A.
30.56×104
B.
3.056×105
C.
3.06×105
D.
3.1×105
若数m用四舍五入法取得近似数为1.6,则m的取值范围是(
)
.
A.
m=1.6
B.
1.55≤m<1.65
C.
1.55<m≤1.65
D.
1.55≤m<1.56
用式子表示“引入相反数后,加减混合运算可以统一为加法运算”,正确的是(
)
A.
a+b-c=a+b+c
B.
a-b+c=a+b-c
C.
a+b-c=a+(-b)+(-c)
D.
a+b-c=a+b+(-c)
下列各组数中数值相等的是(
)
A.
32与23
B.
-23与(-2)3
C.
-32与(-3)2
D.
[-2×(-3)]2与2×(-3)2
一辆汽车行驶10km,耗油2L,根据下面里程表推算,汽车在这段路程中耗油(
)??L。
A.
39
B.
74
C.
113
D.
1170
现规定一种运算“△”,x△y=2x·2y,如3△2=23·22=25=32,则4△8的结果是(
)
A.
211
B.
212
C.
232
D.
32
一根绳子剪成两段,第一段长米,第二段占全长的,那么下列三种说法正确的是(
)。
A.
第一段长
B.
第二段长
C.
两段一样长
D.
无法确定
一个池塘的水浮莲,每天都在生长,且每天的面积是前一天的2倍,如果12天就能把整个池塘遮满,那么水浮莲长到遮住半个池塘需要(
)
A.
6天
B.
8天
C.
10天
D.
11天
二、填空题(本大题共9小题,共30.0分)
若有理数a,b满足|3a-1|+(b-2)2=0,则ab的值为________.
以“万”为单位,准确数5万与近似数5万最多相差________.
近似数2.12×104精确到_______位.
若a、b互为相反数,c、d互为倒数,则2a+2b-cd=______.
若两个数的积得-1,称它们互为负倒数,则-0.125的负倒数是________.
_________.
若,则用把连接起来为????????????
.
公交车从起点开始经过A,B,C,D四站到达终点,各站上下车人数如下(上车为正,下车为负)例如(7,-4)表示该站上车7人,下车4人.现在起点站有15人,A(4,-8),B(6,-5),C(7,-3),D(1,-4).车上乘客最多时有_____名.
观察下列等式1,,,
将以上三个等式两边分别相加得:11.
(1)猜想并写出:____;
(2)直接写出下列各式的计算结果:____;
(3)探究并计算:____.
三、计算题(本大题共1小题,共8.0分)
计算:
(1)(-6)-(-)18.
(2)(-)3.
-+|5-9|+243.
(4)-50(-)-1.
四、解答题(本大题共5小题,共32.0分)
某超市进了240瓶绿茶饮料,第一天卖出这批饮料总数的,第二夫卖出这批饮料总数的,问还有多少瓶绿茶饮料没卖出?
小王和小明利用温差法测量某山峰的高度,他们于同一时刻测得山顶温度为-1.1℃,山脚温度为1.6℃.已知该地区山峰的高度每增加100m,气温大约降低0.6℃,问这个山峰的高度大约是多少米?
用一批纸装订同样的练习本,如果每本30页,可以装订80本.如果每本页数减少,这批纸可以装订多少本?
一份书稿,甲单独打字要12小时完成,乙单独打字要18小时完成。如果先由甲打1小时,然后由乙接替甲打1小时,再由甲接替乙打1小时……两人如此交替工作。那么,打完这份书稿,甲、乙二人共用多少小时?
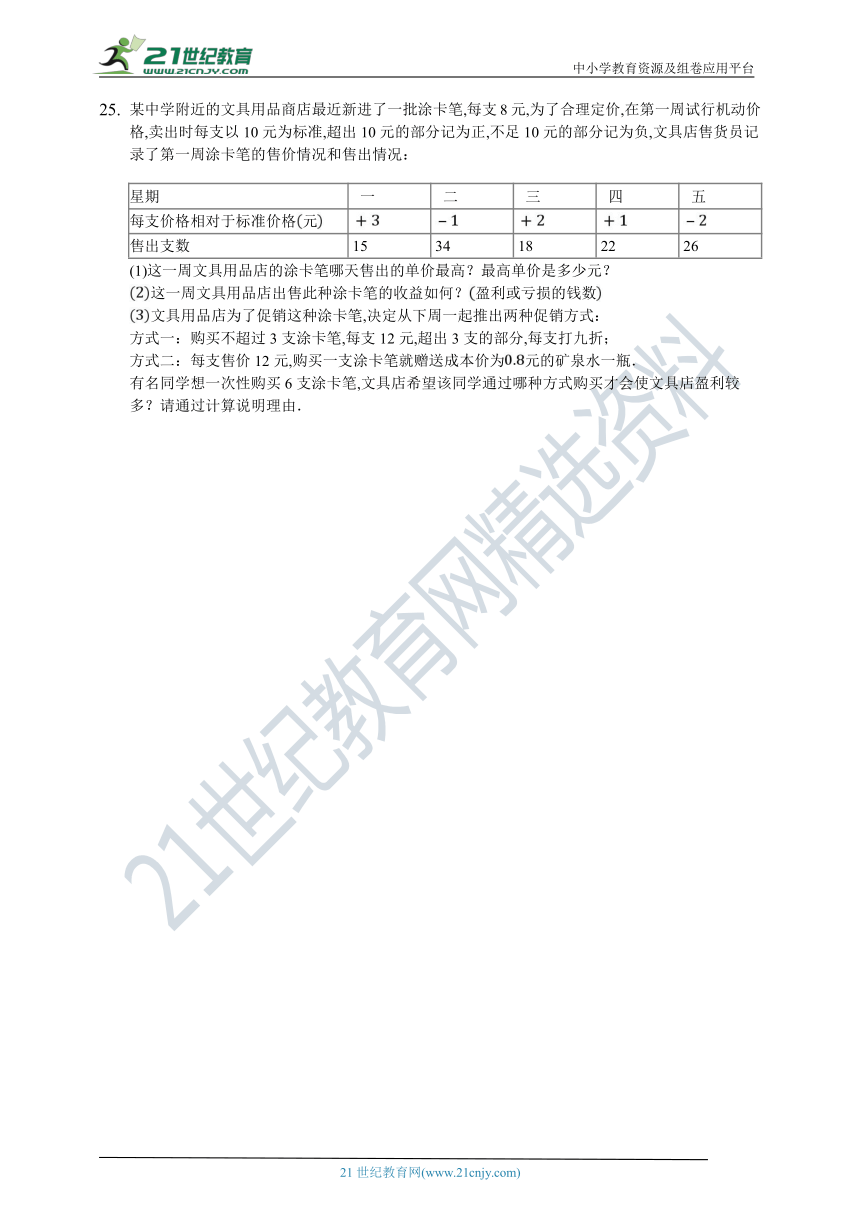
某中学附近的文具用品商店最近新进了一批涂卡笔,每支8元,为了合理定价,在第一周试行机动价格,卖出时每支以10元为标准,超出10元的部分记为正,不足10元的部分记为负,文具店售货员记录了第一周涂卡笔的售价情况和售出情况:
星期
?
一
?
二
?
三
?
四
?
五
每支价格相对于标准价格元
?
?
?
?
?
售出支数
?15
?34
?18
?22
?26
(1)这一周文具用品店的涂卡笔哪天售出的单价最高?最高单价是多少元?
这一周文具用品店出售此种涂卡笔的收益如何?盈利或亏损的钱数
文具用品店为了促销这种涂卡笔,决定从下周一起推出两种促销方式:
方式一:购买不超过3支涂卡笔,每支12元,超出3支的部分,每支打九折;
方式二:每支售价12元,购买一支涂卡笔就赠送成本价为元的矿泉水一瓶.
有名同学想一次性购买6支涂卡笔,文具店希望该同学通过哪种方式购买才会使文具店盈利较多?请通过计算说明理由.
答案和解析
1.【答案】D
【解析】此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.设“■”表示的数是x,根据题意列出方程,求出方程的解即可得到结果.
2.【答案】D
【解析】略
3.【答案】B
【解析】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.?
4.【答案】B
【解析】本题考查了四舍五入取近似值的方法,注意十分位上的6,有可能是百分位上舍去得到的,也有可能是百分位上进位得到的.根据四舍五入的方法,十分位有可能是5,则百分位是不小于5的数,若十分位是6,则百分位是不大于4的数.正确理解四舍五入法,解答本题应该思考近似数等于1.6的最小的数不能小于多少,最大的数不能大于多少,从这个角度即可得解.
5.【答案】D
【解析】本题考查的是有理数的加、减混合运算,注意相反数概念的利用.
利用减去一个数等于加上这个数的相反数,进行变化即可.
6.【答案】B
【解析】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.原式各项利用乘方的意义计算得到结果,即可做出判断.
7.【答案】A
【解析】本题考查有理数的混合运算,属于基础题,比较简单.
根据题意得:(L),故选A.
8.【答案】B
【解析】略
9.【答案】B
【解析】本题考查有理数的减法及有理数的大小比较.根据第二段占全长的可知第一段占全长的,据此即可知第二段比第一段长.
10.【答案】D
【解析】本题考查有理数的乘方,涉及数字规律问题.设第一天水浮莲的面积为a,根据题意可知第二天水浮莲的面积为:2a,第三天的面积为4a,如此类推可知:第12天水浮莲的面积即为池塘面积为212-1a,进而可求解.
11.【答案】
【解析】本题考查的知识点是非负数的性质-绝对值和偶次方,代数式求值,首先根据绝对值和偶次方非负数的性质求出a,b,再代入代数式求值即可.
a=,b=2,∴
12.【答案】5000
【解析】本题主要考查了近似数,关键是熟练掌握四舍五入法,根据四舍五入法确定近似数的范围,然后计算差即可.
近似数5万可以由最小45000和最大54999四舍五入得到,又因为50000-45000=5000,54999-50000=4999,5000>4999,
所以准确数5万与近似数5万最多相差5000.
13.【答案】百
【解析】本题考查的是近似数有关知识,掌握确定一个近似数精确到哪位的方法,即可完成.确定近似数精确到哪一位,就是看这个数的最后一位是什么位.
精确到百位.
14.【答案】-1
【解析】根据题意得:a+b=0,cd=1,则原式=2(a+b)-cd=-1
利用相反数,倒数的性质求出各自的值,代入原式计算即可求出值.
此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
15.【答案】8
【解析】本题主要考查了倒数,关键是熟练掌握负倒数的定义.根据乘积为-1的两个数互为负倒数可得结果.
16.【答案】-
【解析】此题考查有理数的混合运算的灵活应用,关键是总结规律,还要会确定符号.可把括号里的数通分,再确定符号,由于有1998-1000+1=999个因式,所以符号为负,最后约分即可.
原式=-?.
17.【答案】a<-b<b<-a.
【解析】本题考查了相反数,绝对值,有理数加法法则、有理数大小的比较等知识点,熟练掌握各知识点是解题的关键.
18.【答案】16
【解析】本题考查正负数,解答本题的关键是明确正负数在题目中的实际意义.根据题意可以算出各个阶段对应的乘客人数,从而可以解答本题.
由题意可得,起点到A站之间,车上有15人,
A站到B站之间,车上有:15+4-8=11(人),
B站到C站之间,车上有:11+6-5=12(人),
C站到D站之间,车上有:12+7-3=16(人),
D站到终点之间,车上有:16+1-4=13(人),
由上可得,车上乘客最多有16人
19.【答案】,,???
【解析】本题综合考查了有理数的混合运算,数字变化中的恒等变形裂项法,互为相反数的两个数和为0等知识点,重点掌握数字变化中的恒等变形裂项相消法.
(1)由已知等式猜想;
(2)由一项变成两项,根据两个数互为相反数,最后所求加数的和等于首项、尾项的和,即为1=;
(3)由第(2)小题的方法可得
20.【答案】(1)原式=(-6)×-(-)18
=-9+12
=3;
(2)原式=×-×
=-1
=;
(3)原式=-9+4+8
=3;
(4)原式=8-50×(-)-1
=8+-1
=.
【解析】本题考查有理数的混合运算,掌握有理数的混合运算法则是解题的关键,注意有理数的运算顺序.(1)先算乘法和除法,再加减即可;
(2)运用分配律分别相乘后,再相减即可;
(3)先算乘方再算绝对值和除法,最后相加即可;
(4)先算乘方,再算乘除,最后加减即可.
21.【答案】100瓶
(瓶),
即还有100瓶绿茶饮料没卖出.
【解析】本题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
根据题意表示出第一天与第二天卖出饮料,即可求出没有卖出的饮料.
22.【答案】450米?
[1.6-(-1.1)]÷0.6×100=2.7÷0.6×100=450(米)
【解析】本题利用了正负数的意义和有理数的乘除运算.
山顶与山脚的温度差可表示为1.6-(-1.1),再除以0.6后乘以100,即为山顶高度.
23.【答案】100本
30×80=2400(页),30×(1-?)=24(页),2400÷24=100(本).?
【解析】本题考查分数的混合运算的应用,解答的关键是求出这批纸一共有多少页.根据“如果每本30页,可以装订80本”,用乘法即可求出总页数,根据“每本页数减少”,用乘法即可求得每本的页数,最后用除法求出装订的本数即可.
24.【答案】小时
甲乙合作,需要的天数:(小时),
各干7个小时后,还剩,
甲来完成这,用的时间:(小时),
所以总共用(小时)
【解析】本题考查的是有理数的混合运算有关知识,首先根据题意找出题目中的关系,然后列式进行计算即可解答.
25.【答案】(1)根据表格可得:星期一的售价最高,售价是:10+3=13(元);
(2)15×3+2×18+1×22-34×1-26×2=17(元),
(15+34+18+22+26)×(10-8)=230(元),
230+17=247(元),故盈利247元;
(3)方式一的花费:12×3+(6-3)×12×0.9=68.4(元),
方式二的花费:12×6-0.8×6=67.2(元),
∵68.4>67.2,
∴文具店希望该同学通过方式一购买才会使文具店盈利较多.
【解析】此题主要考查了正负数的意义和有理数的混合运算,关键是掌握正负数表示两种具有相反意义的量.(1)根据表格数据可直接得到答案;(2)首先算出以10元为标准时的赢利情况,再算出10元一支时的盈利情况,然后相加即可;(3)分别以两种收费方式计算出这名同学一次性购买6支涂卡笔的花费,然后进行比较即可得到答案.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
七年级数学上册有理数的运算单元测试卷
(满分100分)
题号
一
二
三
四
总分
得分
一、选择题(本大题共10小题,共30.0分)
小明做了这样一道计算题:|(-3)+■|,其中“■”表示被墨水污染看不到的一个数,他分析了后边的答案得知该题的计算结果为16,那么“■”表示的数应该是(
)
A.
13
B.
-13
C.
19
D.
-13或19
在下列式子:①5×(-4)×(-2);②;③(-4)4;④(-3)5中.其中,计算结果是负数的有?
(???
)
①②
B.
①②③
C.
①③④
D.
②④
某市人口数约是305600人,这个数用科学记数法表示为(
)
A.
30.56×104
B.
3.056×105
C.
3.06×105
D.
3.1×105
若数m用四舍五入法取得近似数为1.6,则m的取值范围是(
)
.
A.
m=1.6
B.
1.55≤m<1.65
C.
1.55<m≤1.65
D.
1.55≤m<1.56
用式子表示“引入相反数后,加减混合运算可以统一为加法运算”,正确的是(
)
A.
a+b-c=a+b+c
B.
a-b+c=a+b-c
C.
a+b-c=a+(-b)+(-c)
D.
a+b-c=a+b+(-c)
下列各组数中数值相等的是(
)
A.
32与23
B.
-23与(-2)3
C.
-32与(-3)2
D.
[-2×(-3)]2与2×(-3)2
一辆汽车行驶10km,耗油2L,根据下面里程表推算,汽车在这段路程中耗油(
)??L。
A.
39
B.
74
C.
113
D.
1170
现规定一种运算“△”,x△y=2x·2y,如3△2=23·22=25=32,则4△8的结果是(
)
A.
211
B.
212
C.
232
D.
32
一根绳子剪成两段,第一段长米,第二段占全长的,那么下列三种说法正确的是(
)。
A.
第一段长
B.
第二段长
C.
两段一样长
D.
无法确定
一个池塘的水浮莲,每天都在生长,且每天的面积是前一天的2倍,如果12天就能把整个池塘遮满,那么水浮莲长到遮住半个池塘需要(
)
A.
6天
B.
8天
C.
10天
D.
11天
二、填空题(本大题共9小题,共30.0分)
若有理数a,b满足|3a-1|+(b-2)2=0,则ab的值为________.
以“万”为单位,准确数5万与近似数5万最多相差________.
近似数2.12×104精确到_______位.
若a、b互为相反数,c、d互为倒数,则2a+2b-cd=______.
若两个数的积得-1,称它们互为负倒数,则-0.125的负倒数是________.
_________.
若,则用把连接起来为????????????
.
公交车从起点开始经过A,B,C,D四站到达终点,各站上下车人数如下(上车为正,下车为负)例如(7,-4)表示该站上车7人,下车4人.现在起点站有15人,A(4,-8),B(6,-5),C(7,-3),D(1,-4).车上乘客最多时有_____名.
观察下列等式1,,,
将以上三个等式两边分别相加得:11.
(1)猜想并写出:____;
(2)直接写出下列各式的计算结果:____;
(3)探究并计算:____.
三、计算题(本大题共1小题,共8.0分)
计算:
(1)(-6)-(-)18.
(2)(-)3.
-+|5-9|+243.
(4)-50(-)-1.
四、解答题(本大题共5小题,共32.0分)
某超市进了240瓶绿茶饮料,第一天卖出这批饮料总数的,第二夫卖出这批饮料总数的,问还有多少瓶绿茶饮料没卖出?
小王和小明利用温差法测量某山峰的高度,他们于同一时刻测得山顶温度为-1.1℃,山脚温度为1.6℃.已知该地区山峰的高度每增加100m,气温大约降低0.6℃,问这个山峰的高度大约是多少米?
用一批纸装订同样的练习本,如果每本30页,可以装订80本.如果每本页数减少,这批纸可以装订多少本?
一份书稿,甲单独打字要12小时完成,乙单独打字要18小时完成。如果先由甲打1小时,然后由乙接替甲打1小时,再由甲接替乙打1小时……两人如此交替工作。那么,打完这份书稿,甲、乙二人共用多少小时?
某中学附近的文具用品商店最近新进了一批涂卡笔,每支8元,为了合理定价,在第一周试行机动价格,卖出时每支以10元为标准,超出10元的部分记为正,不足10元的部分记为负,文具店售货员记录了第一周涂卡笔的售价情况和售出情况:
星期
?
一
?
二
?
三
?
四
?
五
每支价格相对于标准价格元
?
?
?
?
?
售出支数
?15
?34
?18
?22
?26
(1)这一周文具用品店的涂卡笔哪天售出的单价最高?最高单价是多少元?
这一周文具用品店出售此种涂卡笔的收益如何?盈利或亏损的钱数
文具用品店为了促销这种涂卡笔,决定从下周一起推出两种促销方式:
方式一:购买不超过3支涂卡笔,每支12元,超出3支的部分,每支打九折;
方式二:每支售价12元,购买一支涂卡笔就赠送成本价为元的矿泉水一瓶.
有名同学想一次性购买6支涂卡笔,文具店希望该同学通过哪种方式购买才会使文具店盈利较多?请通过计算说明理由.
答案和解析
1.【答案】D
【解析】此题考查了有理数的加法,熟练掌握运算法则是解本题的关键.设“■”表示的数是x,根据题意列出方程,求出方程的解即可得到结果.
2.【答案】D
【解析】略
3.【答案】B
【解析】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.?
4.【答案】B
【解析】本题考查了四舍五入取近似值的方法,注意十分位上的6,有可能是百分位上舍去得到的,也有可能是百分位上进位得到的.根据四舍五入的方法,十分位有可能是5,则百分位是不小于5的数,若十分位是6,则百分位是不大于4的数.正确理解四舍五入法,解答本题应该思考近似数等于1.6的最小的数不能小于多少,最大的数不能大于多少,从这个角度即可得解.
5.【答案】D
【解析】本题考查的是有理数的加、减混合运算,注意相反数概念的利用.
利用减去一个数等于加上这个数的相反数,进行变化即可.
6.【答案】B
【解析】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.原式各项利用乘方的意义计算得到结果,即可做出判断.
7.【答案】A
【解析】本题考查有理数的混合运算,属于基础题,比较简单.
根据题意得:(L),故选A.
8.【答案】B
【解析】略
9.【答案】B
【解析】本题考查有理数的减法及有理数的大小比较.根据第二段占全长的可知第一段占全长的,据此即可知第二段比第一段长.
10.【答案】D
【解析】本题考查有理数的乘方,涉及数字规律问题.设第一天水浮莲的面积为a,根据题意可知第二天水浮莲的面积为:2a,第三天的面积为4a,如此类推可知:第12天水浮莲的面积即为池塘面积为212-1a,进而可求解.
11.【答案】
【解析】本题考查的知识点是非负数的性质-绝对值和偶次方,代数式求值,首先根据绝对值和偶次方非负数的性质求出a,b,再代入代数式求值即可.
a=,b=2,∴
12.【答案】5000
【解析】本题主要考查了近似数,关键是熟练掌握四舍五入法,根据四舍五入法确定近似数的范围,然后计算差即可.
近似数5万可以由最小45000和最大54999四舍五入得到,又因为50000-45000=5000,54999-50000=4999,5000>4999,
所以准确数5万与近似数5万最多相差5000.
13.【答案】百
【解析】本题考查的是近似数有关知识,掌握确定一个近似数精确到哪位的方法,即可完成.确定近似数精确到哪一位,就是看这个数的最后一位是什么位.
精确到百位.
14.【答案】-1
【解析】根据题意得:a+b=0,cd=1,则原式=2(a+b)-cd=-1
利用相反数,倒数的性质求出各自的值,代入原式计算即可求出值.
此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
15.【答案】8
【解析】本题主要考查了倒数,关键是熟练掌握负倒数的定义.根据乘积为-1的两个数互为负倒数可得结果.
16.【答案】-
【解析】此题考查有理数的混合运算的灵活应用,关键是总结规律,还要会确定符号.可把括号里的数通分,再确定符号,由于有1998-1000+1=999个因式,所以符号为负,最后约分即可.
原式=-?.
17.【答案】a<-b<b<-a.
【解析】本题考查了相反数,绝对值,有理数加法法则、有理数大小的比较等知识点,熟练掌握各知识点是解题的关键.
18.【答案】16
【解析】本题考查正负数,解答本题的关键是明确正负数在题目中的实际意义.根据题意可以算出各个阶段对应的乘客人数,从而可以解答本题.
由题意可得,起点到A站之间,车上有15人,
A站到B站之间,车上有:15+4-8=11(人),
B站到C站之间,车上有:11+6-5=12(人),
C站到D站之间,车上有:12+7-3=16(人),
D站到终点之间,车上有:16+1-4=13(人),
由上可得,车上乘客最多有16人
19.【答案】,,???
【解析】本题综合考查了有理数的混合运算,数字变化中的恒等变形裂项法,互为相反数的两个数和为0等知识点,重点掌握数字变化中的恒等变形裂项相消法.
(1)由已知等式猜想;
(2)由一项变成两项,根据两个数互为相反数,最后所求加数的和等于首项、尾项的和,即为1=;
(3)由第(2)小题的方法可得
20.【答案】(1)原式=(-6)×-(-)18
=-9+12
=3;
(2)原式=×-×
=-1
=;
(3)原式=-9+4+8
=3;
(4)原式=8-50×(-)-1
=8+-1
=.
【解析】本题考查有理数的混合运算,掌握有理数的混合运算法则是解题的关键,注意有理数的运算顺序.(1)先算乘法和除法,再加减即可;
(2)运用分配律分别相乘后,再相减即可;
(3)先算乘方再算绝对值和除法,最后相加即可;
(4)先算乘方,再算乘除,最后加减即可.
21.【答案】100瓶
(瓶),
即还有100瓶绿茶饮料没卖出.
【解析】本题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
根据题意表示出第一天与第二天卖出饮料,即可求出没有卖出的饮料.
22.【答案】450米?
[1.6-(-1.1)]÷0.6×100=2.7÷0.6×100=450(米)
【解析】本题利用了正负数的意义和有理数的乘除运算.
山顶与山脚的温度差可表示为1.6-(-1.1),再除以0.6后乘以100,即为山顶高度.
23.【答案】100本
30×80=2400(页),30×(1-?)=24(页),2400÷24=100(本).?
【解析】本题考查分数的混合运算的应用,解答的关键是求出这批纸一共有多少页.根据“如果每本30页,可以装订80本”,用乘法即可求出总页数,根据“每本页数减少”,用乘法即可求得每本的页数,最后用除法求出装订的本数即可.
24.【答案】小时
甲乙合作,需要的天数:(小时),
各干7个小时后,还剩,
甲来完成这,用的时间:(小时),
所以总共用(小时)
【解析】本题考查的是有理数的混合运算有关知识,首先根据题意找出题目中的关系,然后列式进行计算即可解答.
25.【答案】(1)根据表格可得:星期一的售价最高,售价是:10+3=13(元);
(2)15×3+2×18+1×22-34×1-26×2=17(元),
(15+34+18+22+26)×(10-8)=230(元),
230+17=247(元),故盈利247元;
(3)方式一的花费:12×3+(6-3)×12×0.9=68.4(元),
方式二的花费:12×6-0.8×6=67.2(元),
∵68.4>67.2,
∴文具店希望该同学通过方式一购买才会使文具店盈利较多.
【解析】此题主要考查了正负数的意义和有理数的混合运算,关键是掌握正负数表示两种具有相反意义的量.(1)根据表格数据可直接得到答案;(2)首先算出以10元为标准时的赢利情况,再算出10元一支时的盈利情况,然后相加即可;(3)分别以两种收费方式计算出这名同学一次性购买6支涂卡笔的花费,然后进行比较即可得到答案.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
