第二章 简单事件的概率单元测试题(含解析)
文档属性
| 名称 | 第二章 简单事件的概率单元测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-02 16:13:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上第二章简单事件的概率
习题精选
一.选择题(共15小题)
1.(2020?恩施州)“彩缕碧筠粽,香粳白玉团”.端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是( )
A. B. C. D.
2.(2020?营口)某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
3.(2020?呼和浩特)已知电流在一定时间段内正常通过电子元件“”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.05 D.025
4.(2020?绥化)在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )
A. B. C. D.
5.(2019?齐齐哈尔)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为( )
A.27 B.23 C.22 D.18
6.(2019?泰州)小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20 B.300 C.500 D.800
7.(2020?绍兴)如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球从E出口落出的概率是( )
A. B. C. D.
8.(2019?宜昌)在“践行生态文明,你我一起行动”主题有奖竞赛活动中,903班共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,如果参赛同学抽到每一类别的可能性相同,那么小宇参赛时抽到“生态知识”的概率是( )
A. B. C. D.
9.(2019?台湾)箱子内装有53颗白球及2颗红球,小芬打算从箱子内抽球,以每次抽出一球后将球再放回的方式抽53次球.若箱子内每颗球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小芬抽到红球的机率为何?( )
A. B. C. D.
10.(2018?玉林)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
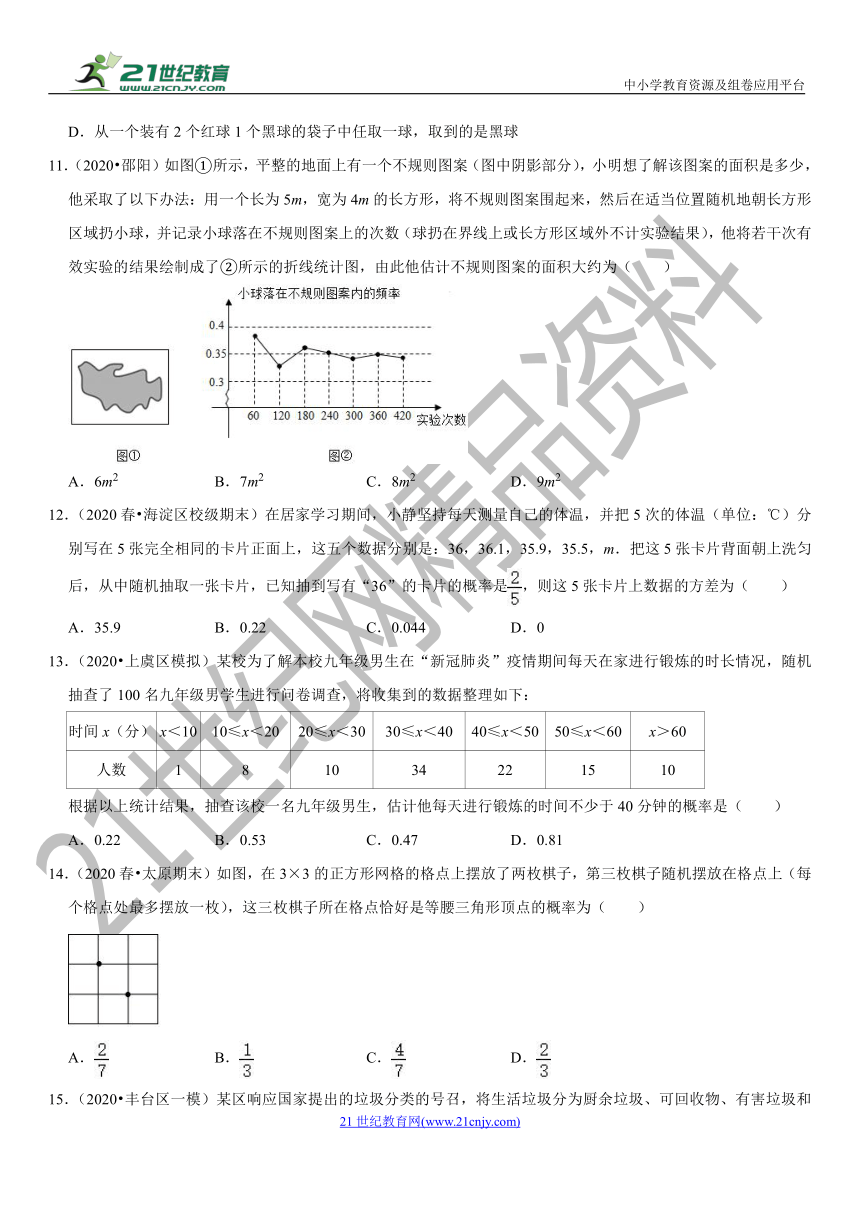
11.(2020?邵阳)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计实验结果),他将若干次有效实验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2 B.7m2 C.8m2 D.9m2
12.(2020春?海淀区校级期末)在居家学习期间,小静坚持每天测量自己的体温,并把5次的体温(单位:℃)分别写在5张完全相同的卡片正面上,这五个数据分别是:36,36.1,35.9,35.5,m.把这5张卡片背面朝上洗匀后,从中随机抽取一张卡片,已知抽到写有“36”的卡片的概率是,则这5张卡片上数据的方差为( )
A.35.9 B.0.22 C.0.044 D.0
13.(2020?上虞区模拟)某校为了解本校九年级男生在“新冠肺炎”疫情期间每天在家进行锻炼的时长情况,随机抽查了100名九年级男学生进行问卷调查,将收集到的数据整理如下:
时间x(分) x<10 10≤x<20 20≤x<30 30≤x<40 40≤x<50 50≤x<60 x>60
人数 1 8 10 34 22 15 10
根据以上统计结果,抽查该校一名九年级男生,估计他每天进行锻炼的时间不少于40分钟的概率是( )
A.0.22 B.0.53 C.0.47 D.0.81
14.(2020春?太原期末)如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是等腰三角形顶点的概率为( )
A. B. C. D.
15.(2020?丰台区一模)某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类 垃圾量
垃圾种类(吨) “厨余垃圾”箱 “可回收物”箱 “有害垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 40 60
可回收物 30 140 10 20
有害垃圾 5 20 60 15
其他垃圾 25 15 20 40
下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是( )
A.0 B.1 C.2 D.3
二.填空题(共10小题)
16.(2020?益阳)小朋友甲的口袋中有6粒弹珠,其中2粒红色,4粒绿色,他随机拿出1颗送给小朋友乙,则送出的弹珠颜色为红色的概率是 .
17.(2020?张家界)新学期开学,刚刚组建的七年级(1)班有男生30人,女生24人,欲从该班级中选出一名值日班长,任何人都有同样的机会,则这班选中一名男生当值日班长的概率是 .
18.(2020?新疆)表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数n 200 500 800 2000 12000
成活的棵数m 187 446 730 1790 10836
成活的频率 0.935 0.892 0.913 0.895 0.903
由此估计这种苹果树苗移植成活的概率约为 .(精确到0.1)
19.(2020?宜昌)技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 .(结果要求保留两位小数)
20.(2020?雅安)从﹣,﹣1,1,2,5中任取一数作为a,使抛物线y=ax2+bx+c的开口向上的概率为 .
21.(2019?湘潭)为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是 .
22.(2020春?沙坪坝区校级期末)在四张完全相同的卡片上分别写上﹣,0,1,2四个数字,然后放入一个不透明的袋子中摇匀,现从中随机抽取第一张卡片记下数字a,放回摇匀.然后随机抽取第二张卡片记下数字b,且a+b=m,则m的值使关于x的一元二次方程(m﹣)x2+2x+1=0有实数解的概率是 .
23.(2020春?成都期末)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.现再将n个白球放入布袋,搅匀后,使摸出1个红球的概率为,则n的值为 .
24.(2020春?沙坪坝区校级期末)设计一个摸球游戏,先在一个不透明的盒子中放入2个白球,如果希望从中任意摸出1个球是白球的概率为,那么应该向盒子中再放入 个其他颜色的球.(游戏用球除颜色外均相同)
25.(2020春?锦江区期末)已知m是不等式组的正整数解,则分式方程=有整数解的概率为 .
三.解答题(共8小题)
26.(2020春?市中区校级期末)已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
(1)求从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入2个白球,求从口袋中随机收出一个白球的概率是多少?
27.(2020?荆门)如图是某商场第二季度某品牌运动服装的S号,M号,L号,XL号,XXL号销售情况的扇形统计图和条形统计图.
根据图中信息解答下列问题:
(1)求XL号,XXL号运动服装销量的百分比;
(2)补全条形统计图;
(3)按照M号,XL号运动服装的销量比,从M号、XL号运动服装中分别取出x件、y件,若再取2件XL号运动服装,将它们放在一起,现从这(x+y+2)件运动服装中,随机取出1件,取得M号运动服装的概率为,求x,y的值.
28.(2019?雅安)某校为了解本校学生对课后服务情况的评价,随机抽取了部分学生进行调查,根据调查结果制成了如下不完整的统计图.
根据统计图:
(1)求该校被调查的学生总数及评价为“满意”的人数;
(2)补全折线统计图;
(3)根据调查结果,若要在全校学生中随机抽1名学生,估计该学生的评价为“非常满意”或“满意”的概率是多少?
29.(2020春?沈河区期末)某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是 ;
(2)该班小丽同学能有幸去参加游学活动的概率是 ;
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?
30.(2020春?姑苏区期末)某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生.其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 .扇形统计图中喜欢“戏曲”部分扇形的圆心角为 度.
(2)请你补全条形统计图.
(3)某班7位同学中,1人喜欢舞蹈,2人喜欢乐器,1人喜欢声乐,3人喜欢乐曲,李老师要从这7人中任选1人参加学校社团展演,则恰好选出1人喜欢乐器的概率是 .
31.(2020春?彭州市期末)如图,现有一个均匀的转盘被平均分成8等份,分别标有2、4、6、8、10、12、14、16这8个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,无效,重转).
(1)转动转盘,转出的数字是4的倍数的概率是多少;
(2)小明和小红进行游戏:各自转相同的次数,指针指向3的倍数则小明胜,指针指向4的倍数则小红胜,这个游戏公平吗?为什么?如果让你根据这个转盘来设计一个公平的游戏,你会怎么设计呢?
32.(2020?黑龙江)为了提高学生体质,战胜疫情,某中学组织全校学生宅家一分钟跳绳比赛,全校跳绳平均成绩是每分钟99次,某班班长统计了全班50名学生一分钟跳绳成绩,列出的频数分布直方图如图所示,(每个小组包括左端点,不包括右端点).
求:(1)该班一分钟跳绳的平均次数至少是多少,是否超过全校的平均次数;
(2)该班的一个学生说:“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围;
(3)从该班中任选一人,其跳绳次数超过全校平均数的概率是多少.
33.(2020春?江阴市期中)在一个不透明的盒子里装有黑、白两种颜色的球共100只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 70 124 190 325 538 670 2004
摸到白球的频率 0.70 0.62 0.633 0.65 0.6725 0.670 0.668
(1)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为 ;(精确到0.01)
(2)试估算盒子里黑球有 只;
(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是 .A.从一副扑克牌中任意抽取一张,这张牌是“红色的”B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5.
浙教版九年级上第二章简单事件的概率
习题精选
参考答案与试题解析
一.选择题(共15小题)
1.(2020?恩施州)“彩缕碧筠粽,香粳白玉团”.端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是( )
A. B. C. D.
【解答】解:由题意可得:粽子总数为11个,其中6个为甜粽,
所以选到甜粽的概率为:,
故选:D.
2.(2020?营口)某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
【解答】解:∵从频率的波动情况可以发现频率稳定在0.82附近,
∴这名运动员射击一次时“射中九环以上”的概率是0.82.
故选:B.
3.(2020?呼和浩特)已知电流在一定时间段内正常通过电子元件“”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.05 D.025
【解答】解:根据题意,电流在一定时间段内正常通过电子元件的概率是0.5,
即某一个电子元件不正常工作的概率为0.5,
则两个元件同时不正常工作的概率为0.25;
故在一定时间段内AB之间电流能够正常通过的概率为=0.75,
故选:A.
4.(2020?绥化)在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )
A. B. C. D.
【解答】解:∵袋子中一共有(m+n+3)个小球,其中红球有3个,
∴任意摸出一个球是红球的概率是,
故选:B.
5.(2019?齐齐哈尔)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为( )
A.27 B.23 C.22 D.18
【解答】解:设袋中黑球的个数为x,
根据题意得=,解得x=22,
即袋中黑球的个数为22个.
故选:C.
6.(2019?泰州)小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20 B.300 C.500 D.800
【解答】解:观察表格发现:随着实验次数的增加,正面朝上的频率逐渐稳定到0.5附近,
所以抛掷硬币的次数为1000,则“正面朝上”的频数最接近1000×0.5=500次,
故选:C.
7.(2020?绍兴)如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球从E出口落出的概率是( )
A. B. C. D.
【解答】解:由图可知,在每个交叉口都有向左或向右两种可能,且可能性相等,
小球最终落出的点共有E、F、G、H四个,
所以小球从E出口落出的概率是:;
故选:C.
8.(2019?宜昌)在“践行生态文明,你我一起行动”主题有奖竞赛活动中,903班共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,如果参赛同学抽到每一类别的可能性相同,那么小宇参赛时抽到“生态知识”的概率是( )
A. B. C. D.
【解答】解:∵共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,参赛同学抽到每一类别的可能性相同,
∴小宇参赛时抽到“生态知识”的概率是:.
故选:B.
9.(2019?台湾)箱子内装有53颗白球及2颗红球,小芬打算从箱子内抽球,以每次抽出一球后将球再放回的方式抽53次球.若箱子内每颗球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小芬抽到红球的机率为何?( )
A. B. C. D.
【解答】解:∵一个盒子内装有大小、形状相同的53+2=55个球,其中红球2个,白球53个,
∴小芬抽到红球的概率是:=.
故选:D.
10.(2018?玉林)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
【解答】解:A、抛一枚硬币,出现正面朝上的概率为0.5,不符合这一结果,故此选项错误;
B、掷一个正六面体的骰子,出现3点朝上为,不符合这一结果,故此选项错误;
C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为:0.25,不符合这一结果,故此选项错误;
D、从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球的概率为:,符合这一结果,故此选项正确.
故选:D.
11.(2020?邵阳)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计实验结果),他将若干次有效实验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2 B.7m2 C.8m2 D.9m2
【解答】解:假设不规则图案面积为x,
由已知得:长方形面积为20,
根据几何概率公式小球落在不规则图案的概率为:,
当事件A实验次数足够多,即样本足够大时,其频率可作为事件A发生的概率估计值,故由折线图可知,小球落在不规则图案的概率大约为0.35,
综上有:,解得x=7.
故选:B.
12.(2020春?海淀区校级期末)在居家学习期间,小静坚持每天测量自己的体温,并把5次的体温(单位:℃)分别写在5张完全相同的卡片正面上,这五个数据分别是:36,36.1,35.9,35.5,m.把这5张卡片背面朝上洗匀后,从中随机抽取一张卡片,已知抽到写有“36”的卡片的概率是,则这5张卡片上数据的方差为( )
A.35.9 B.0.22 C.0.044 D.0
【解答】解:∵抽到写有“36”的卡片的概率是,
∴卡片中36的个数为5×=2,
则这组数据为36,36.1,35.9,35.5,36,
∵==35.9,
∴方差为×[2×(36﹣35.9)2+(36.1﹣35.9)2+(35.9﹣35.9)2+(35.5﹣35.9)2]=0.044,
故选:C.
13.(2020?上虞区模拟)某校为了解本校九年级男生在“新冠肺炎”疫情期间每天在家进行锻炼的时长情况,随机抽查了100名九年级男学生进行问卷调查,将收集到的数据整理如下:
时间x(分) x<10 10≤x<20 20≤x<30 30≤x<40 40≤x<50 50≤x<60 x>60
人数 1 8 10 34 22 15 10
根据以上统计结果,抽查该校一名九年级男生,估计他每天进行锻炼的时间不少于40分钟的概率是( )
A.0.22 B.0.53 C.0.47 D.0.81
【解答】解:估计他每天进行锻炼的时间不少于40分钟的概率是=0.47,
故选:C.
14.(2020春?太原期末)如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是等腰三角形顶点的概率为( )
A. B. C. D.
【解答】解:由图知第三枚棋子可摆放的位置共有14种,其中这三枚棋子所在格点恰好是等腰三角形顶点的有8种,
∴这三枚棋子所在格点恰好是等腰三角形顶点的概率为=,
故选:C.
15.(2020?丰台区一模)某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类 垃圾量
垃圾种类(吨) “厨余垃圾”箱 “可回收物”箱 “有害垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 40 60
可回收物 30 140 10 20
有害垃圾 5 20 60 15
其他垃圾 25 15 20 40
下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【解答】解:(1)厨余垃圾投放错误的有100+40+60=200t;故错误;
(2)估计可回收物投放正确的概率约为=;故正确;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普,故正确.
故选:C.
二.填空题(共10小题)
16.(2020?益阳)小朋友甲的口袋中有6粒弹珠,其中2粒红色,4粒绿色,他随机拿出1颗送给小朋友乙,则送出的弹珠颜色为红色的概率是 .
【解答】解:∵口袋中有6粒弹珠,随机拿出1颗共有6种等可能结果,其中送出的弹珠颜色为红色的有2种结果,
∴送出的弹珠颜色为红色的概率是=,
故答案为:.
17.(2020?张家界)新学期开学,刚刚组建的七年级(1)班有男生30人,女生24人,欲从该班级中选出一名值日班长,任何人都有同样的机会,则这班选中一名男生当值日班长的概率是 .
【解答】解:全班共有学生30+24=54(人),
其中男生30人,
则这班选中一名男生当值日班长的概率是=.
故答案为:.
18.(2020?新疆)表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数n 200 500 800 2000 12000
成活的棵数m 187 446 730 1790 10836
成活的频率 0.935 0.892 0.913 0.895 0.903
由此估计这种苹果树苗移植成活的概率约为 0.9 .(精确到0.1)
【解答】解:根据表格数据可知:
苹果树苗移植成活的频率近似值为0.9,
所以估计这种苹果树苗移植成活的概率约为0.9.
故答案为:0.9.
19.(2020?宜昌)技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 0.99 .(结果要求保留两位小数)
【解答】解:∵抽检某一产品2020件,发现产品合格的频率已达到0.9911,
∴依此我们可以估计该产品合格的概率为0.99,
故答案为:0.99.
20.(2020?雅安)从﹣,﹣1,1,2,5中任取一数作为a,使抛物线y=ax2+bx+c的开口向上的概率为 .
【解答】解:在所列的5个数中任取一个数有5种等可能结果,其中使抛物线y=ax2+bx+c的开口向上的有3种结果,
∴使抛物线y=ax2+bx+c的开口向上的概率为,
故答案为:.
21.(2019?湘潭)为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是 .
【解答】解:选出的恰为女生的概率为,
故答案为.
22.(2020春?沙坪坝区校级期末)在四张完全相同的卡片上分别写上﹣,0,1,2四个数字,然后放入一个不透明的袋子中摇匀,现从中随机抽取第一张卡片记下数字a,放回摇匀.然后随机抽取第二张卡片记下数字b,且a+b=m,则m的值使关于x的一元二次方程(m﹣)x2+2x+1=0有实数解的概率是 .
【解答】解:∴关于x的一元二次方程(m﹣)x2+2x+1=0有实数解,
∴b2﹣4ac≥0,且m﹣≠0,
即:4﹣4(m﹣)≥0,且m﹣≠0,
∴m≤且m≠,
由列表法表示m所有等可能出现的结果情况如下:
共有16种等可能出现的结果,其中m≤且m≠的有11种,
∴m的值使关于x的一元二次方程(m﹣)x2+2x+1=0有实数解的概率为.
23.(2020春?成都期末)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.现再将n个白球放入布袋,搅匀后,使摸出1个红球的概率为,则n的值为 3 .
【解答】解:由题意得,
=,
解得,n=3,
经检验,n=3是原方程的解,
所以原方程的解为n=3,
故答案为:3.
24.(2020春?沙坪坝区校级期末)设计一个摸球游戏,先在一个不透明的盒子中放入2个白球,如果希望从中任意摸出1个球是白球的概率为,那么应该向盒子中再放入 6 个其他颜色的球.(游戏用球除颜色外均相同)
【解答】解:由题意知袋子中共有小球2÷=8(个),
∴需要向盒子放入其它颜色的球的个数为8﹣2=6(个),
故答案为:6.
25.(2020春?锦江区期末)已知m是不等式组的正整数解,则分式方程=有整数解的概率为 .
【解答】解:解不等式m﹣2≤3m﹣10,得m≥4,
所以不等式组的解集为4≤m<8,
∴正整数m=4,5,6,7.
分式方程去分母得:2(x+1)=m(x﹣2),
整理,得(m﹣2)x=2m+2,
当m﹣2≠0即m≠2时,x=,
即x=2+,
∵分式方程有整数解,且x≠2,x≠﹣1,
∴m=4,5,
∴分式方程=有整数解的概率为:=.
故答案为:.
三.解答题(共8小题)
26.(2020春?市中区校级期末)已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
(1)求从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入2个白球,求从口袋中随机收出一个白球的概率是多少?
【解答】解:(1)∵一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球,
∴从中随机抽取出一个黑球的概率是:;
(2)∵往口袋中再放入2个白球,
∴共有9个球,其中白球有5个,
∴往口袋中再放入2个白球,从口袋中随机收出一个白球的概率是.
27.(2020?荆门)如图是某商场第二季度某品牌运动服装的S号,M号,L号,XL号,XXL号销售情况的扇形统计图和条形统计图.
根据图中信息解答下列问题:
(1)求XL号,XXL号运动服装销量的百分比;
(2)补全条形统计图;
(3)按照M号,XL号运动服装的销量比,从M号、XL号运动服装中分别取出x件、y件,若再取2件XL号运动服装,将它们放在一起,现从这(x+y+2)件运动服装中,随机取出1件,取得M号运动服装的概率为,求x,y的值.
【解答】解:(1)60÷30%=200(件),
×100%=10%,
1﹣25%﹣30%﹣20%﹣10%=15%.
故XL号,XXL号运动服装销量的百分比分别为15%,10%;
(2)S号服装销量:200×25%=50(件),
L号服装销量:200×20%=40(件),
XL号服装销量:200×15%=30(件),
条形统计图补充如下:
(3)由题意,得,
解得.
故所求x,y的值分别为12,6.
28.(2019?雅安)某校为了解本校学生对课后服务情况的评价,随机抽取了部分学生进行调查,根据调查结果制成了如下不完整的统计图.
根据统计图:
(1)求该校被调查的学生总数及评价为“满意”的人数;
(2)补全折线统计图;
(3)根据调查结果,若要在全校学生中随机抽1名学生,估计该学生的评价为“非常满意”或“满意”的概率是多少?
【解答】解:(1)由折线统计图知“非常满意”9人,由扇形统计图知“非常满意”占15%,所以被调查学生总数为9÷15%=60(人),所以“满意”的人数为60﹣(9+21+3)=27(人);
(2)如图:
(3)所求概率为=.
29.(2020春?沈河区期末)某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是 ;
(2)该班小丽同学能有幸去参加游学活动的概率是 ;
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?
【解答】解:(1)该班小明同学恰好抽到丙类名额的概率==.
故答案为:;
(2)该班小丽同学能有幸去参加实践活动的概率==.
故答案为:;
(3)设还要争取甲类名额x个,
根据题意得=24%,解得x=8,
答:要求抽到甲类的概率要达到24%,则还要争取甲类名额8个.
30.(2020春?姑苏区期末)某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 50 名学生.其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 24% .扇形统计图中喜欢“戏曲”部分扇形的圆心角为 28.8 度.
(2)请你补全条形统计图.
(3)某班7位同学中,1人喜欢舞蹈,2人喜欢乐器,1人喜欢声乐,3人喜欢乐曲,李老师要从这7人中任选1人参加学校社团展演,则恰好选出1人喜欢乐器的概率是 .
【解答】解:(1)在这次调查中,一共抽查了8÷16%=50名学生,
其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为:×100%=24%,
扇形统计图中喜欢“戏曲”部分扇形的圆心角为:360°×=28.8°,
故答案为:50,24%,28.8;
(2)喜欢戏曲的学生有:50﹣12﹣16﹣8﹣10=4(人),
补全的条形统计图如右图所示;
(3)∵某班7位同学中,1人喜欢舞蹈,2人喜欢乐器,1人喜欢声乐,3人喜欢乐曲,
∴李老师要从这7人中任选1人参加学校社团展演,则恰好选出1人喜欢乐器的概率是,
故答案为:.
31.(2020春?彭州市期末)如图,现有一个均匀的转盘被平均分成8等份,分别标有2、4、6、8、10、12、14、16这8个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,无效,重转).
(1)转动转盘,转出的数字是4的倍数的概率是多少;
(2)小明和小红进行游戏:各自转相同的次数,指针指向3的倍数则小明胜,指针指向4的倍数则小红胜,这个游戏公平吗?为什么?如果让你根据这个转盘来设计一个公平的游戏,你会怎么设计呢?
【解答】解:(1)转动转盘,转出的数字是4的倍数的概率==;
(2)这个游戏不公平.
理由如下:转动一次,指针指向3的倍数的结果数为2,所以小明胜的概率==,
指针指向4的倍数的结果数为4,所以小红胜的概率==,
而>,
所以这个游戏不公平.
设计一个公平的游戏可为:各自转相同的次数,指针指向不是4的倍数则小明胜,指针指向是4的倍数则小红胜.
32.(2020?黑龙江)为了提高学生体质,战胜疫情,某中学组织全校学生宅家一分钟跳绳比赛,全校跳绳平均成绩是每分钟99次,某班班长统计了全班50名学生一分钟跳绳成绩,列出的频数分布直方图如图所示,(每个小组包括左端点,不包括右端点).
求:(1)该班一分钟跳绳的平均次数至少是多少,是否超过全校的平均次数;
(2)该班的一个学生说:“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围;
(3)从该班中任选一人,其跳绳次数超过全校平均数的概率是多少.
【解答】解:(1)该班一分钟跳绳的平均次数至少是:=100.8,
∵100.8>100,
∴超过全校的平均次数;
(2)这个学生的跳绳成绩在该班是中位数,因为4+13+19=36,所以中位数一定在100~120范围内;
(3)该班60秒跳绳成绩大于或等于100次的有:19+7+5+2=33(人),
故从该班中任选一人,其跳绳次数超过全校平均数的概率是.
33.(2020春?江阴市期中)在一个不透明的盒子里装有黑、白两种颜色的球共100只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 70 124 190 325 538 670 2004
摸到白球的频率 0.70 0.62 0.633 0.65 0.6725 0.670 0.668
(1)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为 0.67 ;(精确到0.01)
(2)试估算盒子里黑球有 33 只;
(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是 C .A.从一副扑克牌中任意抽取一张,这张牌是“红色的”B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5.
【解答】解:(1)由表可知,若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为0.67,
故答案为:0.67;
(2)根据题意得:
100×(1﹣0.67)=33(只),
答:盒子里黑球有33只;
故答案为:33;
(3)A.从一副扑克牌中任意抽取一张,这张牌是“红色的”的概率为==0.5<0.67,故此选项不符合题意;
B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”的概率为=0.5,不符合题意;
C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5的概率为≈0.67,符合题意;
所以某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是C,
故答案为:C.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/8/2 13:06:54;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
浙教版九年级上第二章简单事件的概率
习题精选
一.选择题(共15小题)
1.(2020?恩施州)“彩缕碧筠粽,香粳白玉团”.端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是( )
A. B. C. D.
2.(2020?营口)某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
3.(2020?呼和浩特)已知电流在一定时间段内正常通过电子元件“”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.05 D.025
4.(2020?绥化)在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )
A. B. C. D.
5.(2019?齐齐哈尔)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为( )
A.27 B.23 C.22 D.18
6.(2019?泰州)小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20 B.300 C.500 D.800
7.(2020?绍兴)如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球从E出口落出的概率是( )
A. B. C. D.
8.(2019?宜昌)在“践行生态文明,你我一起行动”主题有奖竞赛活动中,903班共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,如果参赛同学抽到每一类别的可能性相同,那么小宇参赛时抽到“生态知识”的概率是( )
A. B. C. D.
9.(2019?台湾)箱子内装有53颗白球及2颗红球,小芬打算从箱子内抽球,以每次抽出一球后将球再放回的方式抽53次球.若箱子内每颗球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小芬抽到红球的机率为何?( )
A. B. C. D.
10.(2018?玉林)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
11.(2020?邵阳)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计实验结果),他将若干次有效实验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2 B.7m2 C.8m2 D.9m2
12.(2020春?海淀区校级期末)在居家学习期间,小静坚持每天测量自己的体温,并把5次的体温(单位:℃)分别写在5张完全相同的卡片正面上,这五个数据分别是:36,36.1,35.9,35.5,m.把这5张卡片背面朝上洗匀后,从中随机抽取一张卡片,已知抽到写有“36”的卡片的概率是,则这5张卡片上数据的方差为( )
A.35.9 B.0.22 C.0.044 D.0
13.(2020?上虞区模拟)某校为了解本校九年级男生在“新冠肺炎”疫情期间每天在家进行锻炼的时长情况,随机抽查了100名九年级男学生进行问卷调查,将收集到的数据整理如下:
时间x(分) x<10 10≤x<20 20≤x<30 30≤x<40 40≤x<50 50≤x<60 x>60
人数 1 8 10 34 22 15 10
根据以上统计结果,抽查该校一名九年级男生,估计他每天进行锻炼的时间不少于40分钟的概率是( )
A.0.22 B.0.53 C.0.47 D.0.81
14.(2020春?太原期末)如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是等腰三角形顶点的概率为( )
A. B. C. D.
15.(2020?丰台区一模)某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类 垃圾量
垃圾种类(吨) “厨余垃圾”箱 “可回收物”箱 “有害垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 40 60
可回收物 30 140 10 20
有害垃圾 5 20 60 15
其他垃圾 25 15 20 40
下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是( )
A.0 B.1 C.2 D.3
二.填空题(共10小题)
16.(2020?益阳)小朋友甲的口袋中有6粒弹珠,其中2粒红色,4粒绿色,他随机拿出1颗送给小朋友乙,则送出的弹珠颜色为红色的概率是 .
17.(2020?张家界)新学期开学,刚刚组建的七年级(1)班有男生30人,女生24人,欲从该班级中选出一名值日班长,任何人都有同样的机会,则这班选中一名男生当值日班长的概率是 .
18.(2020?新疆)表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数n 200 500 800 2000 12000
成活的棵数m 187 446 730 1790 10836
成活的频率 0.935 0.892 0.913 0.895 0.903
由此估计这种苹果树苗移植成活的概率约为 .(精确到0.1)
19.(2020?宜昌)技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 .(结果要求保留两位小数)
20.(2020?雅安)从﹣,﹣1,1,2,5中任取一数作为a,使抛物线y=ax2+bx+c的开口向上的概率为 .
21.(2019?湘潭)为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是 .
22.(2020春?沙坪坝区校级期末)在四张完全相同的卡片上分别写上﹣,0,1,2四个数字,然后放入一个不透明的袋子中摇匀,现从中随机抽取第一张卡片记下数字a,放回摇匀.然后随机抽取第二张卡片记下数字b,且a+b=m,则m的值使关于x的一元二次方程(m﹣)x2+2x+1=0有实数解的概率是 .
23.(2020春?成都期末)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.现再将n个白球放入布袋,搅匀后,使摸出1个红球的概率为,则n的值为 .
24.(2020春?沙坪坝区校级期末)设计一个摸球游戏,先在一个不透明的盒子中放入2个白球,如果希望从中任意摸出1个球是白球的概率为,那么应该向盒子中再放入 个其他颜色的球.(游戏用球除颜色外均相同)
25.(2020春?锦江区期末)已知m是不等式组的正整数解,则分式方程=有整数解的概率为 .
三.解答题(共8小题)
26.(2020春?市中区校级期末)已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
(1)求从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入2个白球,求从口袋中随机收出一个白球的概率是多少?
27.(2020?荆门)如图是某商场第二季度某品牌运动服装的S号,M号,L号,XL号,XXL号销售情况的扇形统计图和条形统计图.
根据图中信息解答下列问题:
(1)求XL号,XXL号运动服装销量的百分比;
(2)补全条形统计图;
(3)按照M号,XL号运动服装的销量比,从M号、XL号运动服装中分别取出x件、y件,若再取2件XL号运动服装,将它们放在一起,现从这(x+y+2)件运动服装中,随机取出1件,取得M号运动服装的概率为,求x,y的值.
28.(2019?雅安)某校为了解本校学生对课后服务情况的评价,随机抽取了部分学生进行调查,根据调查结果制成了如下不完整的统计图.
根据统计图:
(1)求该校被调查的学生总数及评价为“满意”的人数;
(2)补全折线统计图;
(3)根据调查结果,若要在全校学生中随机抽1名学生,估计该学生的评价为“非常满意”或“满意”的概率是多少?
29.(2020春?沈河区期末)某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是 ;
(2)该班小丽同学能有幸去参加游学活动的概率是 ;
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?
30.(2020春?姑苏区期末)某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生.其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 .扇形统计图中喜欢“戏曲”部分扇形的圆心角为 度.
(2)请你补全条形统计图.
(3)某班7位同学中,1人喜欢舞蹈,2人喜欢乐器,1人喜欢声乐,3人喜欢乐曲,李老师要从这7人中任选1人参加学校社团展演,则恰好选出1人喜欢乐器的概率是 .
31.(2020春?彭州市期末)如图,现有一个均匀的转盘被平均分成8等份,分别标有2、4、6、8、10、12、14、16这8个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,无效,重转).
(1)转动转盘,转出的数字是4的倍数的概率是多少;
(2)小明和小红进行游戏:各自转相同的次数,指针指向3的倍数则小明胜,指针指向4的倍数则小红胜,这个游戏公平吗?为什么?如果让你根据这个转盘来设计一个公平的游戏,你会怎么设计呢?
32.(2020?黑龙江)为了提高学生体质,战胜疫情,某中学组织全校学生宅家一分钟跳绳比赛,全校跳绳平均成绩是每分钟99次,某班班长统计了全班50名学生一分钟跳绳成绩,列出的频数分布直方图如图所示,(每个小组包括左端点,不包括右端点).
求:(1)该班一分钟跳绳的平均次数至少是多少,是否超过全校的平均次数;
(2)该班的一个学生说:“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围;
(3)从该班中任选一人,其跳绳次数超过全校平均数的概率是多少.
33.(2020春?江阴市期中)在一个不透明的盒子里装有黑、白两种颜色的球共100只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 70 124 190 325 538 670 2004
摸到白球的频率 0.70 0.62 0.633 0.65 0.6725 0.670 0.668
(1)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为 ;(精确到0.01)
(2)试估算盒子里黑球有 只;
(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是 .A.从一副扑克牌中任意抽取一张,这张牌是“红色的”B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5.
浙教版九年级上第二章简单事件的概率
习题精选
参考答案与试题解析
一.选择题(共15小题)
1.(2020?恩施州)“彩缕碧筠粽,香粳白玉团”.端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是( )
A. B. C. D.
【解答】解:由题意可得:粽子总数为11个,其中6个为甜粽,
所以选到甜粽的概率为:,
故选:D.
2.(2020?营口)某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
【解答】解:∵从频率的波动情况可以发现频率稳定在0.82附近,
∴这名运动员射击一次时“射中九环以上”的概率是0.82.
故选:B.
3.(2020?呼和浩特)已知电流在一定时间段内正常通过电子元件“”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.05 D.025
【解答】解:根据题意,电流在一定时间段内正常通过电子元件的概率是0.5,
即某一个电子元件不正常工作的概率为0.5,
则两个元件同时不正常工作的概率为0.25;
故在一定时间段内AB之间电流能够正常通过的概率为=0.75,
故选:A.
4.(2020?绥化)在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )
A. B. C. D.
【解答】解:∵袋子中一共有(m+n+3)个小球,其中红球有3个,
∴任意摸出一个球是红球的概率是,
故选:B.
5.(2019?齐齐哈尔)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为( )
A.27 B.23 C.22 D.18
【解答】解:设袋中黑球的个数为x,
根据题意得=,解得x=22,
即袋中黑球的个数为22个.
故选:C.
6.(2019?泰州)小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20 B.300 C.500 D.800
【解答】解:观察表格发现:随着实验次数的增加,正面朝上的频率逐渐稳定到0.5附近,
所以抛掷硬币的次数为1000,则“正面朝上”的频数最接近1000×0.5=500次,
故选:C.
7.(2020?绍兴)如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球从E出口落出的概率是( )
A. B. C. D.
【解答】解:由图可知,在每个交叉口都有向左或向右两种可能,且可能性相等,
小球最终落出的点共有E、F、G、H四个,
所以小球从E出口落出的概率是:;
故选:C.
8.(2019?宜昌)在“践行生态文明,你我一起行动”主题有奖竞赛活动中,903班共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,如果参赛同学抽到每一类别的可能性相同,那么小宇参赛时抽到“生态知识”的概率是( )
A. B. C. D.
【解答】解:∵共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,参赛同学抽到每一类别的可能性相同,
∴小宇参赛时抽到“生态知识”的概率是:.
故选:B.
9.(2019?台湾)箱子内装有53颗白球及2颗红球,小芬打算从箱子内抽球,以每次抽出一球后将球再放回的方式抽53次球.若箱子内每颗球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小芬抽到红球的机率为何?( )
A. B. C. D.
【解答】解:∵一个盒子内装有大小、形状相同的53+2=55个球,其中红球2个,白球53个,
∴小芬抽到红球的概率是:=.
故选:D.
10.(2018?玉林)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
【解答】解:A、抛一枚硬币,出现正面朝上的概率为0.5,不符合这一结果,故此选项错误;
B、掷一个正六面体的骰子,出现3点朝上为,不符合这一结果,故此选项错误;
C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为:0.25,不符合这一结果,故此选项错误;
D、从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球的概率为:,符合这一结果,故此选项正确.
故选:D.
11.(2020?邵阳)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计实验结果),他将若干次有效实验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2 B.7m2 C.8m2 D.9m2
【解答】解:假设不规则图案面积为x,
由已知得:长方形面积为20,
根据几何概率公式小球落在不规则图案的概率为:,
当事件A实验次数足够多,即样本足够大时,其频率可作为事件A发生的概率估计值,故由折线图可知,小球落在不规则图案的概率大约为0.35,
综上有:,解得x=7.
故选:B.
12.(2020春?海淀区校级期末)在居家学习期间,小静坚持每天测量自己的体温,并把5次的体温(单位:℃)分别写在5张完全相同的卡片正面上,这五个数据分别是:36,36.1,35.9,35.5,m.把这5张卡片背面朝上洗匀后,从中随机抽取一张卡片,已知抽到写有“36”的卡片的概率是,则这5张卡片上数据的方差为( )
A.35.9 B.0.22 C.0.044 D.0
【解答】解:∵抽到写有“36”的卡片的概率是,
∴卡片中36的个数为5×=2,
则这组数据为36,36.1,35.9,35.5,36,
∵==35.9,
∴方差为×[2×(36﹣35.9)2+(36.1﹣35.9)2+(35.9﹣35.9)2+(35.5﹣35.9)2]=0.044,
故选:C.
13.(2020?上虞区模拟)某校为了解本校九年级男生在“新冠肺炎”疫情期间每天在家进行锻炼的时长情况,随机抽查了100名九年级男学生进行问卷调查,将收集到的数据整理如下:
时间x(分) x<10 10≤x<20 20≤x<30 30≤x<40 40≤x<50 50≤x<60 x>60
人数 1 8 10 34 22 15 10
根据以上统计结果,抽查该校一名九年级男生,估计他每天进行锻炼的时间不少于40分钟的概率是( )
A.0.22 B.0.53 C.0.47 D.0.81
【解答】解:估计他每天进行锻炼的时间不少于40分钟的概率是=0.47,
故选:C.
14.(2020春?太原期末)如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是等腰三角形顶点的概率为( )
A. B. C. D.
【解答】解:由图知第三枚棋子可摆放的位置共有14种,其中这三枚棋子所在格点恰好是等腰三角形顶点的有8种,
∴这三枚棋子所在格点恰好是等腰三角形顶点的概率为=,
故选:C.
15.(2020?丰台区一模)某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类 垃圾量
垃圾种类(吨) “厨余垃圾”箱 “可回收物”箱 “有害垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 40 60
可回收物 30 140 10 20
有害垃圾 5 20 60 15
其他垃圾 25 15 20 40
下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【解答】解:(1)厨余垃圾投放错误的有100+40+60=200t;故错误;
(2)估计可回收物投放正确的概率约为=;故正确;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普,故正确.
故选:C.
二.填空题(共10小题)
16.(2020?益阳)小朋友甲的口袋中有6粒弹珠,其中2粒红色,4粒绿色,他随机拿出1颗送给小朋友乙,则送出的弹珠颜色为红色的概率是 .
【解答】解:∵口袋中有6粒弹珠,随机拿出1颗共有6种等可能结果,其中送出的弹珠颜色为红色的有2种结果,
∴送出的弹珠颜色为红色的概率是=,
故答案为:.
17.(2020?张家界)新学期开学,刚刚组建的七年级(1)班有男生30人,女生24人,欲从该班级中选出一名值日班长,任何人都有同样的机会,则这班选中一名男生当值日班长的概率是 .
【解答】解:全班共有学生30+24=54(人),
其中男生30人,
则这班选中一名男生当值日班长的概率是=.
故答案为:.
18.(2020?新疆)表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数n 200 500 800 2000 12000
成活的棵数m 187 446 730 1790 10836
成活的频率 0.935 0.892 0.913 0.895 0.903
由此估计这种苹果树苗移植成活的概率约为 0.9 .(精确到0.1)
【解答】解:根据表格数据可知:
苹果树苗移植成活的频率近似值为0.9,
所以估计这种苹果树苗移植成活的概率约为0.9.
故答案为:0.9.
19.(2020?宜昌)技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 0.99 .(结果要求保留两位小数)
【解答】解:∵抽检某一产品2020件,发现产品合格的频率已达到0.9911,
∴依此我们可以估计该产品合格的概率为0.99,
故答案为:0.99.
20.(2020?雅安)从﹣,﹣1,1,2,5中任取一数作为a,使抛物线y=ax2+bx+c的开口向上的概率为 .
【解答】解:在所列的5个数中任取一个数有5种等可能结果,其中使抛物线y=ax2+bx+c的开口向上的有3种结果,
∴使抛物线y=ax2+bx+c的开口向上的概率为,
故答案为:.
21.(2019?湘潭)为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是 .
【解答】解:选出的恰为女生的概率为,
故答案为.
22.(2020春?沙坪坝区校级期末)在四张完全相同的卡片上分别写上﹣,0,1,2四个数字,然后放入一个不透明的袋子中摇匀,现从中随机抽取第一张卡片记下数字a,放回摇匀.然后随机抽取第二张卡片记下数字b,且a+b=m,则m的值使关于x的一元二次方程(m﹣)x2+2x+1=0有实数解的概率是 .
【解答】解:∴关于x的一元二次方程(m﹣)x2+2x+1=0有实数解,
∴b2﹣4ac≥0,且m﹣≠0,
即:4﹣4(m﹣)≥0,且m﹣≠0,
∴m≤且m≠,
由列表法表示m所有等可能出现的结果情况如下:
共有16种等可能出现的结果,其中m≤且m≠的有11种,
∴m的值使关于x的一元二次方程(m﹣)x2+2x+1=0有实数解的概率为.
23.(2020春?成都期末)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.现再将n个白球放入布袋,搅匀后,使摸出1个红球的概率为,则n的值为 3 .
【解答】解:由题意得,
=,
解得,n=3,
经检验,n=3是原方程的解,
所以原方程的解为n=3,
故答案为:3.
24.(2020春?沙坪坝区校级期末)设计一个摸球游戏,先在一个不透明的盒子中放入2个白球,如果希望从中任意摸出1个球是白球的概率为,那么应该向盒子中再放入 6 个其他颜色的球.(游戏用球除颜色外均相同)
【解答】解:由题意知袋子中共有小球2÷=8(个),
∴需要向盒子放入其它颜色的球的个数为8﹣2=6(个),
故答案为:6.
25.(2020春?锦江区期末)已知m是不等式组的正整数解,则分式方程=有整数解的概率为 .
【解答】解:解不等式m﹣2≤3m﹣10,得m≥4,
所以不等式组的解集为4≤m<8,
∴正整数m=4,5,6,7.
分式方程去分母得:2(x+1)=m(x﹣2),
整理,得(m﹣2)x=2m+2,
当m﹣2≠0即m≠2时,x=,
即x=2+,
∵分式方程有整数解,且x≠2,x≠﹣1,
∴m=4,5,
∴分式方程=有整数解的概率为:=.
故答案为:.
三.解答题(共8小题)
26.(2020春?市中区校级期末)已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
(1)求从中随机抽取出一个黑球的概率是多少?
(2)若往口袋中再放入2个白球,求从口袋中随机收出一个白球的概率是多少?
【解答】解:(1)∵一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球,
∴从中随机抽取出一个黑球的概率是:;
(2)∵往口袋中再放入2个白球,
∴共有9个球,其中白球有5个,
∴往口袋中再放入2个白球,从口袋中随机收出一个白球的概率是.
27.(2020?荆门)如图是某商场第二季度某品牌运动服装的S号,M号,L号,XL号,XXL号销售情况的扇形统计图和条形统计图.
根据图中信息解答下列问题:
(1)求XL号,XXL号运动服装销量的百分比;
(2)补全条形统计图;
(3)按照M号,XL号运动服装的销量比,从M号、XL号运动服装中分别取出x件、y件,若再取2件XL号运动服装,将它们放在一起,现从这(x+y+2)件运动服装中,随机取出1件,取得M号运动服装的概率为,求x,y的值.
【解答】解:(1)60÷30%=200(件),
×100%=10%,
1﹣25%﹣30%﹣20%﹣10%=15%.
故XL号,XXL号运动服装销量的百分比分别为15%,10%;
(2)S号服装销量:200×25%=50(件),
L号服装销量:200×20%=40(件),
XL号服装销量:200×15%=30(件),
条形统计图补充如下:
(3)由题意,得,
解得.
故所求x,y的值分别为12,6.
28.(2019?雅安)某校为了解本校学生对课后服务情况的评价,随机抽取了部分学生进行调查,根据调查结果制成了如下不完整的统计图.
根据统计图:
(1)求该校被调查的学生总数及评价为“满意”的人数;
(2)补全折线统计图;
(3)根据调查结果,若要在全校学生中随机抽1名学生,估计该学生的评价为“非常满意”或“满意”的概率是多少?
【解答】解:(1)由折线统计图知“非常满意”9人,由扇形统计图知“非常满意”占15%,所以被调查学生总数为9÷15%=60(人),所以“满意”的人数为60﹣(9+21+3)=27(人);
(2)如图:
(3)所求概率为=.
29.(2020春?沈河区期末)某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是 ;
(2)该班小丽同学能有幸去参加游学活动的概率是 ;
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?
【解答】解:(1)该班小明同学恰好抽到丙类名额的概率==.
故答案为:;
(2)该班小丽同学能有幸去参加实践活动的概率==.
故答案为:;
(3)设还要争取甲类名额x个,
根据题意得=24%,解得x=8,
答:要求抽到甲类的概率要达到24%,则还要争取甲类名额8个.
30.(2020春?姑苏区期末)某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 50 名学生.其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 24% .扇形统计图中喜欢“戏曲”部分扇形的圆心角为 28.8 度.
(2)请你补全条形统计图.
(3)某班7位同学中,1人喜欢舞蹈,2人喜欢乐器,1人喜欢声乐,3人喜欢乐曲,李老师要从这7人中任选1人参加学校社团展演,则恰好选出1人喜欢乐器的概率是 .
【解答】解:(1)在这次调查中,一共抽查了8÷16%=50名学生,
其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为:×100%=24%,
扇形统计图中喜欢“戏曲”部分扇形的圆心角为:360°×=28.8°,
故答案为:50,24%,28.8;
(2)喜欢戏曲的学生有:50﹣12﹣16﹣8﹣10=4(人),
补全的条形统计图如右图所示;
(3)∵某班7位同学中,1人喜欢舞蹈,2人喜欢乐器,1人喜欢声乐,3人喜欢乐曲,
∴李老师要从这7人中任选1人参加学校社团展演,则恰好选出1人喜欢乐器的概率是,
故答案为:.
31.(2020春?彭州市期末)如图,现有一个均匀的转盘被平均分成8等份,分别标有2、4、6、8、10、12、14、16这8个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,无效,重转).
(1)转动转盘,转出的数字是4的倍数的概率是多少;
(2)小明和小红进行游戏:各自转相同的次数,指针指向3的倍数则小明胜,指针指向4的倍数则小红胜,这个游戏公平吗?为什么?如果让你根据这个转盘来设计一个公平的游戏,你会怎么设计呢?
【解答】解:(1)转动转盘,转出的数字是4的倍数的概率==;
(2)这个游戏不公平.
理由如下:转动一次,指针指向3的倍数的结果数为2,所以小明胜的概率==,
指针指向4的倍数的结果数为4,所以小红胜的概率==,
而>,
所以这个游戏不公平.
设计一个公平的游戏可为:各自转相同的次数,指针指向不是4的倍数则小明胜,指针指向是4的倍数则小红胜.
32.(2020?黑龙江)为了提高学生体质,战胜疫情,某中学组织全校学生宅家一分钟跳绳比赛,全校跳绳平均成绩是每分钟99次,某班班长统计了全班50名学生一分钟跳绳成绩,列出的频数分布直方图如图所示,(每个小组包括左端点,不包括右端点).
求:(1)该班一分钟跳绳的平均次数至少是多少,是否超过全校的平均次数;
(2)该班的一个学生说:“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围;
(3)从该班中任选一人,其跳绳次数超过全校平均数的概率是多少.
【解答】解:(1)该班一分钟跳绳的平均次数至少是:=100.8,
∵100.8>100,
∴超过全校的平均次数;
(2)这个学生的跳绳成绩在该班是中位数,因为4+13+19=36,所以中位数一定在100~120范围内;
(3)该班60秒跳绳成绩大于或等于100次的有:19+7+5+2=33(人),
故从该班中任选一人,其跳绳次数超过全校平均数的概率是.
33.(2020春?江阴市期中)在一个不透明的盒子里装有黑、白两种颜色的球共100只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 70 124 190 325 538 670 2004
摸到白球的频率 0.70 0.62 0.633 0.65 0.6725 0.670 0.668
(1)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为 0.67 ;(精确到0.01)
(2)试估算盒子里黑球有 33 只;
(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是 C .A.从一副扑克牌中任意抽取一张,这张牌是“红色的”B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5.
【解答】解:(1)由表可知,若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为0.67,
故答案为:0.67;
(2)根据题意得:
100×(1﹣0.67)=33(只),
答:盒子里黑球有33只;
故答案为:33;
(3)A.从一副扑克牌中任意抽取一张,这张牌是“红色的”的概率为==0.5<0.67,故此选项不符合题意;
B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”的概率为=0.5,不符合题意;
C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5的概率为≈0.67,符合题意;
所以某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是C,
故答案为:C.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/8/2 13:06:54;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
同课章节目录
