3.4圆心角-3.5圆周角小节培优精选试题(含解析)
文档属性
| 名称 | 3.4圆心角-3.5圆周角小节培优精选试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-02 16:24:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上第三章3.4—3.5圆心角圆周角习题精选
一.选择题(共12小题)
1.如图,AB是⊙O的直径,若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
2.(2019秋?柯桥区期末)如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
3.(2019秋?吴兴区期中)如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AC=2,BD=2,则⊙O的半径为( )
A. B. C. D.
4.(2020?项城市三模)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
5.(2020?烟台)量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
6.(2020?碑林区校级二模)如图,⊙O的直径AB垂直于弦CD于点E,∠BCD=22.5°,OC=6,则CD的长为( )
A.3 B.6 C.6 D.12
7.(2020?雁塔区校级一模)如图,B、C两点在以AD为直径的半圆O上,若∠ABC=4∠D,且=3,则∠A的度数为( )
A.60° B.66° C.72° D.78°
8.(2020?牡丹江)如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125° B.130° C.135° D.140°
9.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99° B.108° C.110° D.117°
10.(2020?北海模拟)如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
A.2 B.4 C.4 D.8
11.(2020?道里区二模)如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是( )
A. B.3 C.2 D.4
12.(2020?恩平市模拟)如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,=2,点P是OC上的一个动点,则BP+DP的最小值为( )
A.2 B.2 C.2 D.3
二.填空题(共10小题)
13.(2020?望花区二模)如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°圆弧多次复制并首尾连接而成,现有一点P从A(A为坐标原点),以每秒米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为 .
14.(2019秋?蕲春县期中)如图,AB⊙O的直径,CD为⊙O的弦,若AB⊥CD于E,下列结论:①CE=DE,②=.③=,④AC=AD.其中正确的有 (填序号).
15.(2020?聊城)如图,在⊙O中,四边形OABC为菱形,点D在上,则∠ADC的度数是 .
16.(2020?徐州模拟)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=35°,则∠BOC的度数为 °.
17.(2020?徐州模拟)如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,OC长为 .
18.(2020?德阳模拟)如图,⊙O的半径为5cm,弦AB=cm,CD=cm,则弦AC、BD的夹角∠APB的度数为 .
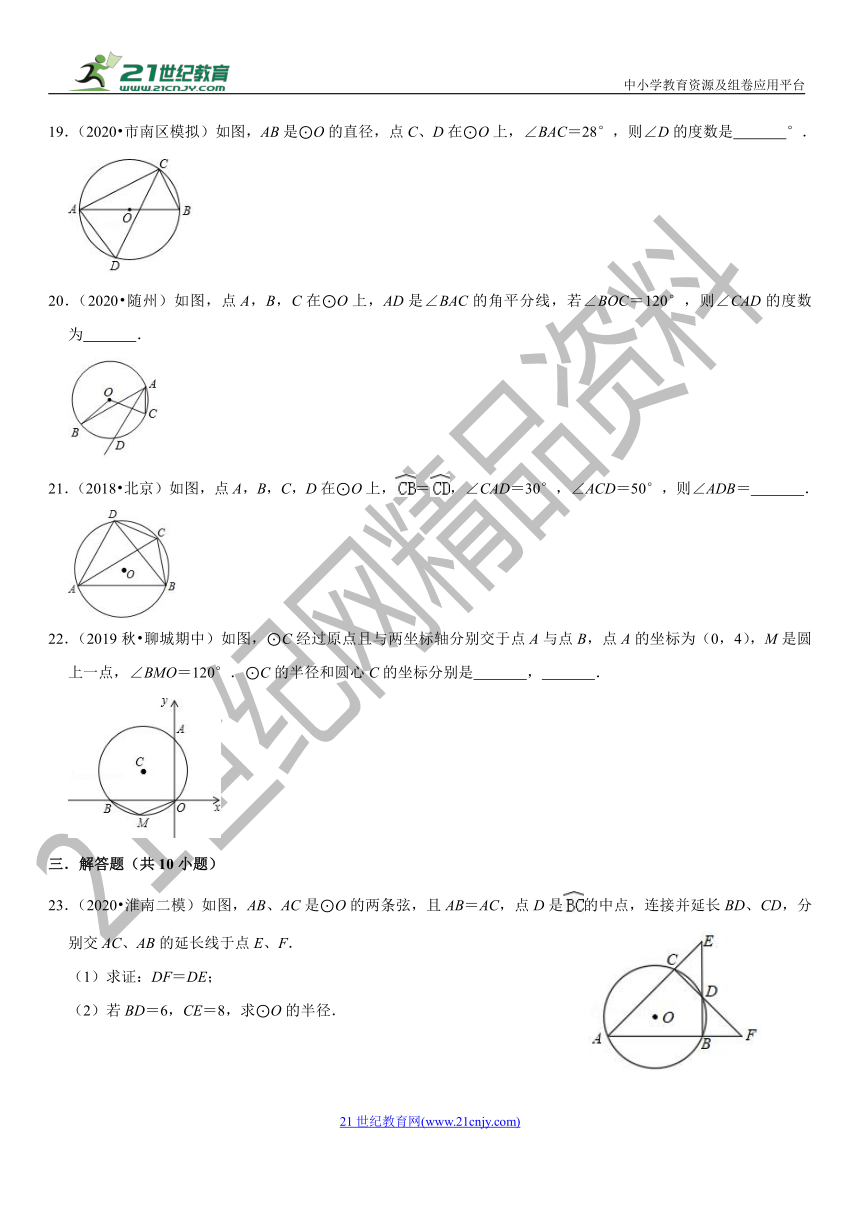
19.(2020?市南区模拟)如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=28°,则∠D的度数是 °.
20.(2020?随州)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120°,则∠CAD的度数为 .
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
22.(2019秋?聊城期中)如图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.⊙C的半径和圆心C的坐标分别是 , .
三.解答题(共10小题)
23.(2020?淮南二模)如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
24.(2020?武汉模拟)如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
25.(2020?南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
26.(2019?包头)如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O半径的长;
(2)求证:AB+BC=BM.
27.(2020?河北区一模)四边形ABCD内接于⊙O,AC为其中一条对角线.
(Ⅰ)如图①,若∠BAD=70°,BC=CD.求∠CAD的大小;
(Ⅱ)如图②,若AD经过圆心O,连接OC,AB=BC,OC∥AB,求∠ACO的大小.
28.(2019秋?襄阳期末)如图,⊙O的半径OA⊥弦BC于E,D是⊙O上一点.
(1)求证:∠ADC=∠AOB;
(2)求AE=2,BC=6,求OA的长.
29.(2020?凉山州一模)如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
30.(2019秋?崇川区校级月考)如图,四边形ABCD内接于⊙O,点E在对角线AC上,若EC=BC,且∠1=∠2.求证:DC=BC.
31.(2019秋?东西湖区期中)如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
32.(2018秋?醴陵市期末)如图,AB是半圆O的直径,C是半圆上一点,=,DH⊥AB于点H,AC分别交BD、DH于E、F.
(1)已知AB=10,AD=6,求AH.
(2)求证:DF=EF
浙教版九年级上第三章3.4—3.5圆心角圆周角
参考答案与试题解析
一.选择题(共12小题)
1.如图,AB是⊙O的直径,若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
【解答】解:∵AD∥OC,
∴∠DAO=∠AOC=70°,
∵OA=OD,
∴∠D=∠A=70°,
∴∠AOD=180°﹣70°﹣70°=40°,
故选:D.
2.(2019秋?柯桥区期末)如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
【解答】解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
3.(2019秋?吴兴区期中)如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AC=2,BD=2,则⊙O的半径为( )
A. B. C. D.
【解答】解:作半径OE⊥AB,连接DE,作BF⊥DE于F,如图,
∵∠DOC=90°,∠BOE=90°,
∴∠DOE=∠AOC,
∴DE=AC=2,
∵∠BDE=180°﹣×90°=135°,
∴∠BDF=45°,
∴DF=BF=BD=×2=2,
在Rt△BEF,BE==2,
∵△BOE为等腰直角三角形,
∴OB=×2=.
故选:D.
4.(2020?项城市三模)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
【解答】解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
5.(2020?烟台)量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
【解答】解:∵OA=OB,∠AOB=140°,
∴∠A=∠B=(180°﹣140°)=20°,
∵∠AOC=60°,
∴∠ADC=∠A+∠AOC=20°+60°=80°,
故选:C.
6.(2020?碑林区校级二模)如图,⊙O的直径AB垂直于弦CD于点E,∠BCD=22.5°,OC=6,则CD的长为( )
A.3 B.6 C.6 D.12
【解答】解:∵AB⊥CD,
∴CE=DE,=,
∴∠BOC=2∠BCD=2×22.5°=45°,
∴△OCE为等腰直角三角形,
∴CE=OC=6×=3,
∴CD=2CE=6.
故选:B.
7.(2020?雁塔区校级一模)如图,B、C两点在以AD为直径的半圆O上,若∠ABC=4∠D,且=3,则∠A的度数为( )
A.60° B.66° C.72° D.78°
【解答】解:连接OC,OB.
∵∠ABC+∠D=180°,∠ABC=4∠D,
∴∠D=36°,
∵OC=DO,
∴∠OCD=∠D=36°,
∴∠DOC=180°﹣36°﹣36°=108°,
∵=3,
∴∠COD=3∠BOC,
∴∠BOC=36°,
∴∠BOD=36°+108°=144°,
∴∠A=∠DOB=72°,
故选:C.
8.(2020?牡丹江)如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125° B.130° C.135° D.140°
【解答】解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵,
∴∠BOC=∠AOC=100°,
∴∠ABC=∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
9.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99° B.108° C.110° D.117°
【解答】解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵=,
∴∠B=∠D=45°,
∵∠DAC=∠COD=×126°=63°,
∴∠AGB=∠DAC+∠D=63°+45°=108°.
故选:B.
10.(2020?北海模拟)如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
A.2 B.4 C.4 D.8
【解答】解:∵AB⊥CD,
∴CE=DE,
∵∠BOC=2∠A=2×22.5°=45°,
∴△OCE为等腰直角三角形,
∴CE=OE=OC=×2=2,
∴CD=2CE=4.
故选:B.
11.(2020?道里区二模)如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是( )
A. B.3 C.2 D.4
【解答】解:设半径OC⊥弦AB于点E,
∴=,
∴∠D=∠BOC=30°,
∴∠BO4=60°,
∴△ODB是等腰直角三角形,
∵OB=2,
∴AE=EB=OB?sin60°=,
∴AB=2AE=2,
故选:C.
12.(2020?恩平市模拟)如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,=2,点P是OC上的一个动点,则BP+DP的最小值为( )
A.2 B.2 C.2 D.3
【解答】解:如图,连接AD,PA,PD,OD.
∵OC⊥AB,OA=OB,
∴PA=PB,∠COB=90°,
∵=2,
∴∠DOB=×90°=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠ABD=60°
∵AB是直径,
∴∠ADB=90°,
∴AD=AB?sin∠ABD=2,
∵PB+PD=PA+PD≥AD,
∴PD+PB≥2,
∴PD+PB的最小值为2,
故选:A.
二.填空题(共10小题)
13.(2020?望花区二模)如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°圆弧多次复制并首尾连接而成,现有一点P从A(A为坐标原点),以每秒米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为 0 .
【解答】解:点运动一个用时为÷π=2秒.
如图,作CD⊥AB于D,与交于点E.
在Rt△ACD中,∵∠ADC=90°,∠ACD=∠ACB=60°,
∴∠CAD=30°,
∴CD=AC=×2=1,
∴DE=CE﹣CD=2﹣1=1,
∴第1秒时点P运动到点E,纵坐标为1;
第2秒时点P运动到点B,纵坐标为0;
第3秒时点P运动到点F,纵坐标为﹣1;
第4秒时点P运动到点G,纵坐标为0;
第5秒时点P运动到点H,纵坐标为1;
…,
∴点P的纵坐标以1,0,﹣1,0四个数为一个周期依次循环,
∵2020÷4=505,
∴第2020秒时点P的纵坐标为是0.
故答案为0.
14.(2019秋?蕲春县期中)如图,AB⊙O的直径,CD为⊙O的弦,若AB⊥CD于E,下列结论:①CE=DE,②=.③=,④AC=AD.其中正确的有 ①②③④ (填序号).
【解答】解:∵AB⊙O的直径,CD为⊙O的弦,AB⊥CD,
∴CE=DE,=,=,①②③正确,
∵=,
∴AC=AD,④正确,
故答案为:①②③④.
15.(2020?聊城)如图,在⊙O中,四边形OABC为菱形,点D在上,则∠ADC的度数是 60° .
【解答】解:∵四边形ABCD内接于⊙O,
∴∠B+∠D=180°,
∵四边形OABC为菱形,
∴∠B=∠AOC,
∴∠D+∠AOC=180°,
∵∠AOC=2∠D,
∴3∠D=180°,
∴∠ADC=60°,
故答案为60°.
16.(2020?徐州模拟)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=35°,则∠BOC的度数为 70 °.
【解答】解:∵OC⊥AB,
∴=,
∴∠BOC=2∠ADC=2×35°=70°.
故答案为70.
17.(2020?徐州模拟)如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,OC长为 .
【解答】解:∵四边形OCDB是平行四边形,点B的坐标为(8,0),
CD∥OA,CD=OB=8,
过点M作MF⊥CD于F,则CF=CD=4,
过C作CE⊥OA于E,
∵A(10,0),
∴OA=10,OM=5,
∴OE=OM﹣ME=OM﹣CF=5﹣4=1,
连接MC,MC=OA=5
∴在Rt△CMF中,
MF===3,
∴CE=MF=3,
∴OC===,
故答案为:.
18.(2020?德阳模拟)如图,⊙O的半径为5cm,弦AB=cm,CD=cm,则弦AC、BD的夹角∠APB的度数为 105° .
【解答】解:连接OA、OB、BC,作直径CE,连接DE,如图,
∵OA=OB=5,AB=5,
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,
∴∠AOB=90°,
∴∠ACB=∠AOB=45°,
∵CE为直径,
∴∠CDE=90°,
∵sin∠E===,
∴∠E=60°,
∴∠PBC=∠E=60°,
∴∠APB=45°+60°=105°.
故答案为105°.
19.(2020?市南区模拟)如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=28°,则∠D的度数是 62 °.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠BAC=28°,
∴∠B=62°
∴∠D=∠B=62°.
故答案为:62.
20.(2020?随州)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120°,则∠CAD的度数为 30° .
【解答】解:∵∠BAC=∠BOC=×120°=60°,
而AD是∠BAC的角平分线,
∴∠CAD=∠BAC=30°.
故答案为30°.
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= 70° .
【解答】解:∵=,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ADB=∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故答案为:70°.
22.(2019秋?聊城期中)如图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.⊙C的半径和圆心C的坐标分别是 4 , (,2) .
【解答】解:连接AB,OC,
∵∠AOB=90°,
∴AB为⊙C的直径,
∵∠BMO=120°,
∴∠BCO=120°,∠BAO=60°,
∵AC=OC,∠BAO=60°,
∴△AOC是等边三角形,
∴⊙C的半径=OA=4;
过C作CD⊥OB于D,则OD=OB,
∵∠BAO=60°,
∴∠ABO=30°,
∴OD===2,CD=BC=×4=2,
∴D点坐标为(﹣2,0),
∴C点坐标为(﹣2,2).
故答案为:4,C(﹣2,2).
三.解答题(共10小题)
23.(2020?淮南二模)如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
【解答】(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
24.(2020?武汉模拟)如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
【解答】证明:∵AB=CD,
∴=,
∴+=+,
∴=,
∴AD=BC.
25.(2020?南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
【解答】证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AF=EF.
26.(2019?包头)如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O半径的长;
(2)求证:AB+BC=BM.
【解答】解:(1)连接OA、OC,过O作OH⊥AC于点H,如图1,
∵∠ABC=120°,
∴∠AMC=180°﹣∠ABC=60°,
∴∠AOC=2∠AMC=120°,
∴∠AOH=∠AOC=60°,
∵AH=AC=,
∴OA=,
故⊙O的半径为2.
(2)证明:在BM上截取BE=BC,连接CE,如图2,
∵∠MBC=60°,BE=BC,
∴△EBC是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°,
∵∠ACM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD,
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°,
∴∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,
∴△ACM是等边三角形,
∴AC=CM,
∴△ACB≌△MCE,
∴AB=ME,
∵ME+EB=BM,
∴AB+BC=BM.
27.(2020?河北区一模)四边形ABCD内接于⊙O,AC为其中一条对角线.
(Ⅰ)如图①,若∠BAD=70°,BC=CD.求∠CAD的大小;
(Ⅱ)如图②,若AD经过圆心O,连接OC,AB=BC,OC∥AB,求∠ACO的大小.
【解答】解:(1)∵BC=CD,
∴=,
∴∠CAD=∠CAB=∠BAD=35°;
(2)连接BD,
∵AB=BC,
∴∠BAC=∠BCA,
∵OC∥AB,
∴∠BAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BAC=∠BCA=∠OAC,
由圆周角定理得,∠BCA=∠BDA,
∴∠BAC=∠BDA=∠OAC,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠ACO=30°.
28.(2019秋?襄阳期末)如图,⊙O的半径OA⊥弦BC于E,D是⊙O上一点.
(1)求证:∠ADC=∠AOB;
(2)求AE=2,BC=6,求OA的长.
【解答】(1)证明:∵OA⊥BC,
∴=,
∴∠ADC=∠AOB;
(2)解:∵OA⊥BC,
∴BE=CE=BC=×6=3,
设⊙O的半径为r,则OA=OB=r,OE=r﹣2,
在Rt△OBE中,32+(r﹣2)2=r2,解得r=,
即OA的长为.
29.(2020?凉山州一模)如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
【解答】解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
30.(2019秋?崇川区校级月考)如图,四边形ABCD内接于⊙O,点E在对角线AC上,若EC=BC,且∠1=∠2.求证:DC=BC.
【解答】证明:∵EC=BC,
∴∠CBE=∠CEB,
∴∠1+∠CBD=∠2+∠BAC,
∵∠1=∠2,
∴∠CBD=∠BAC,
∵∠BAC=∠BDC,
∴∠CBD=∠BDC,
∴BC=CD.
31.(2019秋?东西湖区期中)如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
【解答】证明:(1)连接OB、OC,
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42
解得:x=5,OE=3,
∴半径OA的长=5.
32.(2018秋?醴陵市期末)如图,AB是半圆O的直径,C是半圆上一点,=,DH⊥AB于点H,AC分别交BD、DH于E、F.
(1)已知AB=10,AD=6,求AH.
(2)求证:DF=EF
【解答】(1)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵DH⊥AB,
∴∠DHA=∠ADB=90°,
又∵∠DAB=∠HAD,
∴△DAB∽△HAD,
∴=即=,
∴AH=3.6.
(2)证明:∵=,
∴∠DAC=∠DBA,
∵DH⊥AB,
∴∠FDE+∠B=90°,
∵∠ADB=90°,
∴∠DEF+∠DAC=90°,
∴∠DEF=∠FDE,
∴DF=EF.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/8/2 15:33:35;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
浙教版九年级上第三章3.4—3.5圆心角圆周角习题精选
一.选择题(共12小题)
1.如图,AB是⊙O的直径,若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
2.(2019秋?柯桥区期末)如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
3.(2019秋?吴兴区期中)如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AC=2,BD=2,则⊙O的半径为( )
A. B. C. D.
4.(2020?项城市三模)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
5.(2020?烟台)量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
6.(2020?碑林区校级二模)如图,⊙O的直径AB垂直于弦CD于点E,∠BCD=22.5°,OC=6,则CD的长为( )
A.3 B.6 C.6 D.12
7.(2020?雁塔区校级一模)如图,B、C两点在以AD为直径的半圆O上,若∠ABC=4∠D,且=3,则∠A的度数为( )
A.60° B.66° C.72° D.78°
8.(2020?牡丹江)如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125° B.130° C.135° D.140°
9.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99° B.108° C.110° D.117°
10.(2020?北海模拟)如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
A.2 B.4 C.4 D.8
11.(2020?道里区二模)如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是( )
A. B.3 C.2 D.4
12.(2020?恩平市模拟)如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,=2,点P是OC上的一个动点,则BP+DP的最小值为( )
A.2 B.2 C.2 D.3
二.填空题(共10小题)
13.(2020?望花区二模)如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°圆弧多次复制并首尾连接而成,现有一点P从A(A为坐标原点),以每秒米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为 .
14.(2019秋?蕲春县期中)如图,AB⊙O的直径,CD为⊙O的弦,若AB⊥CD于E,下列结论:①CE=DE,②=.③=,④AC=AD.其中正确的有 (填序号).
15.(2020?聊城)如图,在⊙O中,四边形OABC为菱形,点D在上,则∠ADC的度数是 .
16.(2020?徐州模拟)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=35°,则∠BOC的度数为 °.
17.(2020?徐州模拟)如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,OC长为 .
18.(2020?德阳模拟)如图,⊙O的半径为5cm,弦AB=cm,CD=cm,则弦AC、BD的夹角∠APB的度数为 .
19.(2020?市南区模拟)如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=28°,则∠D的度数是 °.
20.(2020?随州)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120°,则∠CAD的度数为 .
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
22.(2019秋?聊城期中)如图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.⊙C的半径和圆心C的坐标分别是 , .
三.解答题(共10小题)
23.(2020?淮南二模)如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
24.(2020?武汉模拟)如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
25.(2020?南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
26.(2019?包头)如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O半径的长;
(2)求证:AB+BC=BM.
27.(2020?河北区一模)四边形ABCD内接于⊙O,AC为其中一条对角线.
(Ⅰ)如图①,若∠BAD=70°,BC=CD.求∠CAD的大小;
(Ⅱ)如图②,若AD经过圆心O,连接OC,AB=BC,OC∥AB,求∠ACO的大小.
28.(2019秋?襄阳期末)如图,⊙O的半径OA⊥弦BC于E,D是⊙O上一点.
(1)求证:∠ADC=∠AOB;
(2)求AE=2,BC=6,求OA的长.
29.(2020?凉山州一模)如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
30.(2019秋?崇川区校级月考)如图,四边形ABCD内接于⊙O,点E在对角线AC上,若EC=BC,且∠1=∠2.求证:DC=BC.
31.(2019秋?东西湖区期中)如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
32.(2018秋?醴陵市期末)如图,AB是半圆O的直径,C是半圆上一点,=,DH⊥AB于点H,AC分别交BD、DH于E、F.
(1)已知AB=10,AD=6,求AH.
(2)求证:DF=EF
浙教版九年级上第三章3.4—3.5圆心角圆周角
参考答案与试题解析
一.选择题(共12小题)
1.如图,AB是⊙O的直径,若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
【解答】解:∵AD∥OC,
∴∠DAO=∠AOC=70°,
∵OA=OD,
∴∠D=∠A=70°,
∴∠AOD=180°﹣70°﹣70°=40°,
故选:D.
2.(2019秋?柯桥区期末)如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
【解答】解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
3.(2019秋?吴兴区期中)如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AC=2,BD=2,则⊙O的半径为( )
A. B. C. D.
【解答】解:作半径OE⊥AB,连接DE,作BF⊥DE于F,如图,
∵∠DOC=90°,∠BOE=90°,
∴∠DOE=∠AOC,
∴DE=AC=2,
∵∠BDE=180°﹣×90°=135°,
∴∠BDF=45°,
∴DF=BF=BD=×2=2,
在Rt△BEF,BE==2,
∵△BOE为等腰直角三角形,
∴OB=×2=.
故选:D.
4.(2020?项城市三模)如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
【解答】解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
5.(2020?烟台)量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
【解答】解:∵OA=OB,∠AOB=140°,
∴∠A=∠B=(180°﹣140°)=20°,
∵∠AOC=60°,
∴∠ADC=∠A+∠AOC=20°+60°=80°,
故选:C.
6.(2020?碑林区校级二模)如图,⊙O的直径AB垂直于弦CD于点E,∠BCD=22.5°,OC=6,则CD的长为( )
A.3 B.6 C.6 D.12
【解答】解:∵AB⊥CD,
∴CE=DE,=,
∴∠BOC=2∠BCD=2×22.5°=45°,
∴△OCE为等腰直角三角形,
∴CE=OC=6×=3,
∴CD=2CE=6.
故选:B.
7.(2020?雁塔区校级一模)如图,B、C两点在以AD为直径的半圆O上,若∠ABC=4∠D,且=3,则∠A的度数为( )
A.60° B.66° C.72° D.78°
【解答】解:连接OC,OB.
∵∠ABC+∠D=180°,∠ABC=4∠D,
∴∠D=36°,
∵OC=DO,
∴∠OCD=∠D=36°,
∴∠DOC=180°﹣36°﹣36°=108°,
∵=3,
∴∠COD=3∠BOC,
∴∠BOC=36°,
∴∠BOD=36°+108°=144°,
∴∠A=∠DOB=72°,
故选:C.
8.(2020?牡丹江)如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125° B.130° C.135° D.140°
【解答】解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵,
∴∠BOC=∠AOC=100°,
∴∠ABC=∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
9.(2020?青岛)如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99° B.108° C.110° D.117°
【解答】解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵=,
∴∠B=∠D=45°,
∵∠DAC=∠COD=×126°=63°,
∴∠AGB=∠DAC+∠D=63°+45°=108°.
故选:B.
10.(2020?北海模拟)如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
A.2 B.4 C.4 D.8
【解答】解:∵AB⊥CD,
∴CE=DE,
∵∠BOC=2∠A=2×22.5°=45°,
∴△OCE为等腰直角三角形,
∴CE=OE=OC=×2=2,
∴CD=2CE=4.
故选:B.
11.(2020?道里区二模)如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是( )
A. B.3 C.2 D.4
【解答】解:设半径OC⊥弦AB于点E,
∴=,
∴∠D=∠BOC=30°,
∴∠BO4=60°,
∴△ODB是等腰直角三角形,
∵OB=2,
∴AE=EB=OB?sin60°=,
∴AB=2AE=2,
故选:C.
12.(2020?恩平市模拟)如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,=2,点P是OC上的一个动点,则BP+DP的最小值为( )
A.2 B.2 C.2 D.3
【解答】解:如图,连接AD,PA,PD,OD.
∵OC⊥AB,OA=OB,
∴PA=PB,∠COB=90°,
∵=2,
∴∠DOB=×90°=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠ABD=60°
∵AB是直径,
∴∠ADB=90°,
∴AD=AB?sin∠ABD=2,
∵PB+PD=PA+PD≥AD,
∴PD+PB≥2,
∴PD+PB的最小值为2,
故选:A.
二.填空题(共10小题)
13.(2020?望花区二模)如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°圆弧多次复制并首尾连接而成,现有一点P从A(A为坐标原点),以每秒米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为 0 .
【解答】解:点运动一个用时为÷π=2秒.
如图,作CD⊥AB于D,与交于点E.
在Rt△ACD中,∵∠ADC=90°,∠ACD=∠ACB=60°,
∴∠CAD=30°,
∴CD=AC=×2=1,
∴DE=CE﹣CD=2﹣1=1,
∴第1秒时点P运动到点E,纵坐标为1;
第2秒时点P运动到点B,纵坐标为0;
第3秒时点P运动到点F,纵坐标为﹣1;
第4秒时点P运动到点G,纵坐标为0;
第5秒时点P运动到点H,纵坐标为1;
…,
∴点P的纵坐标以1,0,﹣1,0四个数为一个周期依次循环,
∵2020÷4=505,
∴第2020秒时点P的纵坐标为是0.
故答案为0.
14.(2019秋?蕲春县期中)如图,AB⊙O的直径,CD为⊙O的弦,若AB⊥CD于E,下列结论:①CE=DE,②=.③=,④AC=AD.其中正确的有 ①②③④ (填序号).
【解答】解:∵AB⊙O的直径,CD为⊙O的弦,AB⊥CD,
∴CE=DE,=,=,①②③正确,
∵=,
∴AC=AD,④正确,
故答案为:①②③④.
15.(2020?聊城)如图,在⊙O中,四边形OABC为菱形,点D在上,则∠ADC的度数是 60° .
【解答】解:∵四边形ABCD内接于⊙O,
∴∠B+∠D=180°,
∵四边形OABC为菱形,
∴∠B=∠AOC,
∴∠D+∠AOC=180°,
∵∠AOC=2∠D,
∴3∠D=180°,
∴∠ADC=60°,
故答案为60°.
16.(2020?徐州模拟)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=35°,则∠BOC的度数为 70 °.
【解答】解:∵OC⊥AB,
∴=,
∴∠BOC=2∠ADC=2×35°=70°.
故答案为70.
17.(2020?徐州模拟)如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,OC长为 .
【解答】解:∵四边形OCDB是平行四边形,点B的坐标为(8,0),
CD∥OA,CD=OB=8,
过点M作MF⊥CD于F,则CF=CD=4,
过C作CE⊥OA于E,
∵A(10,0),
∴OA=10,OM=5,
∴OE=OM﹣ME=OM﹣CF=5﹣4=1,
连接MC,MC=OA=5
∴在Rt△CMF中,
MF===3,
∴CE=MF=3,
∴OC===,
故答案为:.
18.(2020?德阳模拟)如图,⊙O的半径为5cm,弦AB=cm,CD=cm,则弦AC、BD的夹角∠APB的度数为 105° .
【解答】解:连接OA、OB、BC,作直径CE,连接DE,如图,
∵OA=OB=5,AB=5,
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,
∴∠AOB=90°,
∴∠ACB=∠AOB=45°,
∵CE为直径,
∴∠CDE=90°,
∵sin∠E===,
∴∠E=60°,
∴∠PBC=∠E=60°,
∴∠APB=45°+60°=105°.
故答案为105°.
19.(2020?市南区模拟)如图,AB是⊙O的直径,点C、D在⊙O上,∠BAC=28°,则∠D的度数是 62 °.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠BAC=28°,
∴∠B=62°
∴∠D=∠B=62°.
故答案为:62.
20.(2020?随州)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120°,则∠CAD的度数为 30° .
【解答】解:∵∠BAC=∠BOC=×120°=60°,
而AD是∠BAC的角平分线,
∴∠CAD=∠BAC=30°.
故答案为30°.
21.(2018?北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= 70° .
【解答】解:∵=,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ADB=∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故答案为:70°.
22.(2019秋?聊城期中)如图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.⊙C的半径和圆心C的坐标分别是 4 , (,2) .
【解答】解:连接AB,OC,
∵∠AOB=90°,
∴AB为⊙C的直径,
∵∠BMO=120°,
∴∠BCO=120°,∠BAO=60°,
∵AC=OC,∠BAO=60°,
∴△AOC是等边三角形,
∴⊙C的半径=OA=4;
过C作CD⊥OB于D,则OD=OB,
∵∠BAO=60°,
∴∠ABO=30°,
∴OD===2,CD=BC=×4=2,
∴D点坐标为(﹣2,0),
∴C点坐标为(﹣2,2).
故答案为:4,C(﹣2,2).
三.解答题(共10小题)
23.(2020?淮南二模)如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
【解答】(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
24.(2020?武汉模拟)如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
【解答】证明:∵AB=CD,
∴=,
∴+=+,
∴=,
∴AD=BC.
25.(2020?南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
【解答】证明:(1)∵AC=BC,
∴∠BAC=∠B,
∵DF∥BC,
∴∠ADF=∠B,
∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形;
(2)连接AE,
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B,
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°,
∵BD∥CF,
∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,
∴AF=EF.
26.(2019?包头)如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O半径的长;
(2)求证:AB+BC=BM.
【解答】解:(1)连接OA、OC,过O作OH⊥AC于点H,如图1,
∵∠ABC=120°,
∴∠AMC=180°﹣∠ABC=60°,
∴∠AOC=2∠AMC=120°,
∴∠AOH=∠AOC=60°,
∵AH=AC=,
∴OA=,
故⊙O的半径为2.
(2)证明:在BM上截取BE=BC,连接CE,如图2,
∵∠MBC=60°,BE=BC,
∴△EBC是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°,
∵∠ACM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD,
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°,
∴∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,
∴△ACM是等边三角形,
∴AC=CM,
∴△ACB≌△MCE,
∴AB=ME,
∵ME+EB=BM,
∴AB+BC=BM.
27.(2020?河北区一模)四边形ABCD内接于⊙O,AC为其中一条对角线.
(Ⅰ)如图①,若∠BAD=70°,BC=CD.求∠CAD的大小;
(Ⅱ)如图②,若AD经过圆心O,连接OC,AB=BC,OC∥AB,求∠ACO的大小.
【解答】解:(1)∵BC=CD,
∴=,
∴∠CAD=∠CAB=∠BAD=35°;
(2)连接BD,
∵AB=BC,
∴∠BAC=∠BCA,
∵OC∥AB,
∴∠BAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BAC=∠BCA=∠OAC,
由圆周角定理得,∠BCA=∠BDA,
∴∠BAC=∠BDA=∠OAC,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠ACO=30°.
28.(2019秋?襄阳期末)如图,⊙O的半径OA⊥弦BC于E,D是⊙O上一点.
(1)求证:∠ADC=∠AOB;
(2)求AE=2,BC=6,求OA的长.
【解答】(1)证明:∵OA⊥BC,
∴=,
∴∠ADC=∠AOB;
(2)解:∵OA⊥BC,
∴BE=CE=BC=×6=3,
设⊙O的半径为r,则OA=OB=r,OE=r﹣2,
在Rt△OBE中,32+(r﹣2)2=r2,解得r=,
即OA的长为.
29.(2020?凉山州一模)如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
【解答】解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
30.(2019秋?崇川区校级月考)如图,四边形ABCD内接于⊙O,点E在对角线AC上,若EC=BC,且∠1=∠2.求证:DC=BC.
【解答】证明:∵EC=BC,
∴∠CBE=∠CEB,
∴∠1+∠CBD=∠2+∠BAC,
∵∠1=∠2,
∴∠CBD=∠BAC,
∵∠BAC=∠BDC,
∴∠CBD=∠BDC,
∴BC=CD.
31.(2019秋?东西湖区期中)如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
【解答】证明:(1)连接OB、OC,
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42
解得:x=5,OE=3,
∴半径OA的长=5.
32.(2018秋?醴陵市期末)如图,AB是半圆O的直径,C是半圆上一点,=,DH⊥AB于点H,AC分别交BD、DH于E、F.
(1)已知AB=10,AD=6,求AH.
(2)求证:DF=EF
【解答】(1)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵DH⊥AB,
∴∠DHA=∠ADB=90°,
又∵∠DAB=∠HAD,
∴△DAB∽△HAD,
∴=即=,
∴AH=3.6.
(2)证明:∵=,
∴∠DAC=∠DBA,
∵DH⊥AB,
∴∠FDE+∠B=90°,
∵∠ADB=90°,
∴∠DEF+∠DAC=90°,
∴∠DEF=∠FDE,
∴DF=EF.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/8/2 15:33:35;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
同课章节目录
