平行线的性质和判定

平行线的性质和判定精品资料
教学过程：
一、基础知识点：
1、平行线的性质：
性质1：两条直线被第三条直线所截，如果两条直线平行，那么同位角相等。
简单说成：两直线平行，同位角相等。
几何语言：∵ AB//CD
∴ ∠PMA=∠MNC
性质2：两条直线被第三条直线所截，如果两条直线平行，那么内错角相等。
简单说成：两直线平行，内错角相等。
几何语言：∵ AB//CD
∴ ∠BMN=∠CNM
性质3：两条直线被第三条直线所截，如果两条直线平行，那么同旁内角互补。
简单说成：两直线平行，同旁内角互补。
几何语言：∵ AB//CD
∴ ∠AMN+∠CNM=180°
2、平行线的判定：
几何符号语言：
　（1）∵　∠3＝∠2
　 ∴　AB∥CD（同位角相等，两直线平行）
　（2）∵　∠1＝∠2
　 ∴　AB∥CD（内错角相等，两直线平行）
　（3）∵　∠4＋∠2＝180°
　 ∴　AB∥CD（同旁内角互补，两直线平行）　　　　　　　　　　　　　
3、两条平行线的距离
　如图，直线AB∥CD，EF⊥AB于E，EF⊥CD于F，则称线段EF的长度为两平行线AB与CD间的距离。
　注意：直线AB∥CD，在直线AB上任取一点G，过点G作CD的垂线段GH，则垂线段GH的长度也就是直线AB与CD间的距离。
4、命题：
⑴命题的概念：
判断一件事情的语句，叫做命题。
⑵命题的组成
每个命题都是题设、结论两部分组成。题设是已知事项；结论是由已知事项推出的事项。命题常写成“如果……，那么……”的形式。具有这种形式的命题中，用“如果”开始的部分是题设，用“那么”开始的部分是结论。
　有些命题，没有写成“如果……，那么……”的形式，题设和结论不明显。对于这样的命题，要经过分析才能找出题设和结论，也可以将它们改写成“如果……，那么……”的形式。
注意：命题的题设（条件）部分，有时也可用“已知……”或者“若……”等形式表述；命题的结论部分，有时也可用“求证……”或“则……”等形式表述。
5、平移
（1）、平移变换
　①把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同。
　②新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点
　③连接各组对应点的线段平行且相等
（2）、平移的特征：
　①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化。
　②经过平移后，对应点所连的线段平行（或在同一直线上）且相等。
二、课前小测试：
1．下列命题中，不正确的是____ [ ]
A．两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行
B．两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行
C．两条直线被第三条直线所截，那么这两条直线平行
D．如果两条直线都和第三条直线平行，那么这两条直线也互相平行
2．如图，可以得到DE∥BC的条件是______ [ ]
A．∠ACB=∠BAC B．∠ABC+∠BAE=180° C．∠ACB+∠BAD=180° D．∠ACB=∠BAD
3．如图，直线a、b被直线c所截，现给出下列四个条件:
(1)∠1=∠2，(2)∠3=∠6，(3)∠4+∠7=180°，(4)∠5+∠8=180°，
其中能判定a∥b的条件是_________[ ]
A．(1)(3) B．(2)(4) C．(1)(3)(4) D．(1)(2)(3)(4)
4．一辆汽车在笔直的公路上行驶，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是________[ ]
A．第一次向右拐40°，第二次向左拐40° B．第一次向右拐50°，第二次向左拐130°
C．第一次向右拐50°，第二次向右拐130° D．第一次向左拐50°，第二次向左拐130°
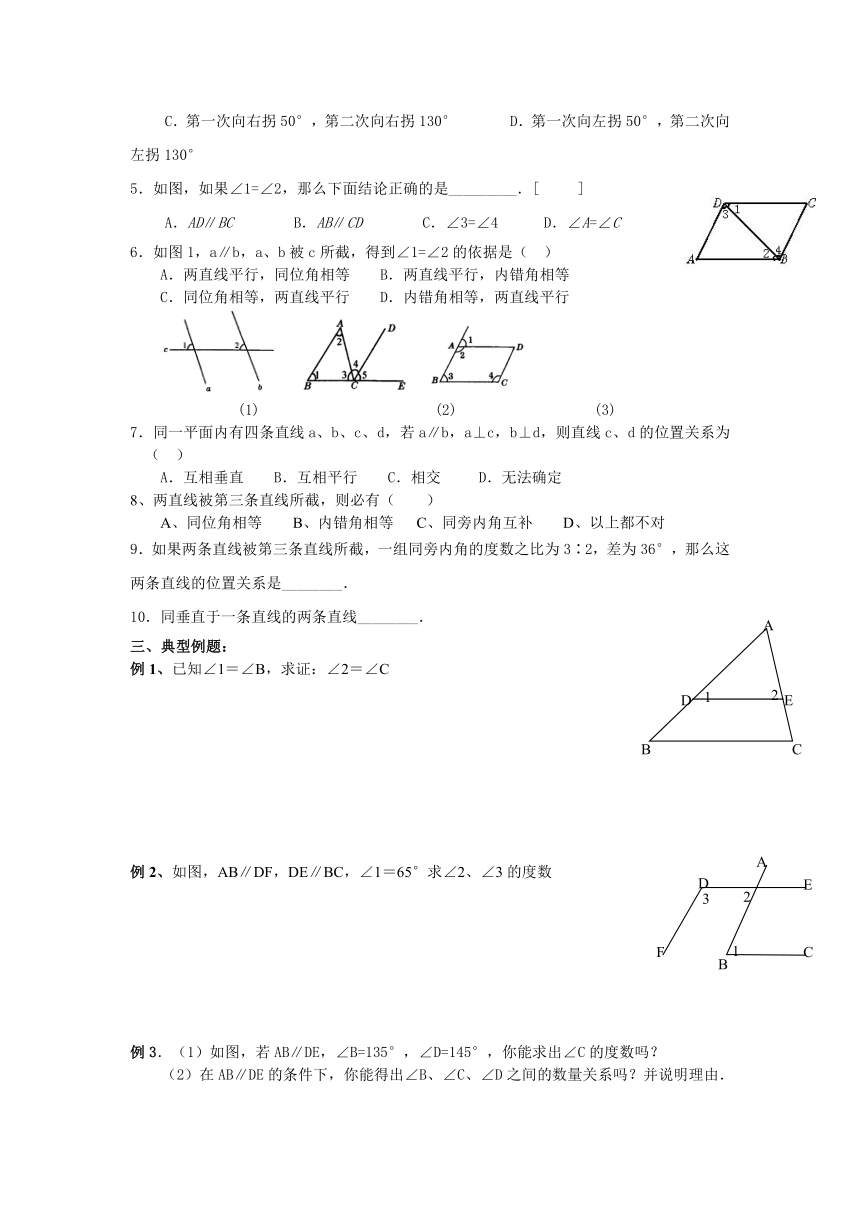
5．如图，如果∠1=∠2，那么下面结论正确的是_________．[ ]
A．AD∥BC B．AB∥CD C．∠3=∠4 D．∠A=∠C
6．如图1，a∥b，a、b被c所截，得到∠1=∠2的依据是（ ）
A．两直线平行，同位角相等 B．两直线平行，内错角相等
C．同位角相等，两直线平行 D．内错角相等，两直线平行
(1) (2) (3)
7．同一平面内有四条直线a、b、c、d，若a∥b，a⊥c，b⊥d，则直线c、d的位置关系为（ ）
A．互相垂直 B．互相平行 C．相交 D．无法确定
8、两直线被第三条直线所截，则必有（ ）
A、同位角相等 B、内错角相等 C、同旁内角互补 D、以上都不对
9．如果两条直线被第三条直线所截，一组同旁内角的度数之比为3∶2，差为36°，那么这两条直线的位置关系是________．
10．同垂直于一条直线的两条直线________．
三、典型例题：
例1、已知∠1＝∠B，求证：∠2＝∠C
例2、如图，AB∥DF，DE∥BC，∠1＝65°求∠2、∠3的度数
例3．（1）如图，若AB∥DE，∠B=135°，∠D=145°，你能求出∠C的度数吗？
（2）在AB∥DE的条件下，你能得出∠B、∠C、∠D之间的数量关系吗？并说明理由．
例4、如图，△ABC经过平移之后成为△DEF，那么：
⑴点A的对应点是点＿＿＿＿＿＿＿＿＿；
⑵点B的对应点是点＿＿＿＿＿＿。
⑶点＿＿＿＿＿的对应点是点F；
⑷线段AB的对应线段是线段＿＿＿＿＿＿＿；
⑸线段BC的对应线段是线段＿＿＿＿＿＿＿；
⑹∠A的对应角是＿＿＿＿＿＿。
　　⑺＿＿＿＿的对应角是∠F。
四、巩固练习：
1、如图，在AB两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48度，A、B两地同时开工，若干天后公路准确接通。
① B地所修公路的走向是南偏西多少度？
② 若公路AB长8千米，另一条公路BC长6千米且BC的走向是北偏西42度，试求A地到公路BC的距离。
2、如图：把一张长方形的纸片ABCD沿EF折叠后，ED交BC于G，点D、C分别落在P、Q位置上，若∠EFG＝55度，求∠1、∠2的度数
3、如图：已知∠1和∠D互余，CF⊥DF，试证明AB∥CD
4、如图已知：AB∥CD，∠1＝40度，∠2＝70度，求∠3的度数
如图所示的是重叠的两个直角三角形，将其中一个三角形沿方向平移得到三角形，如果，则图中阴影部分的面积为
6． 已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DFE的平分线相交于点P．说明∠P＝．
五、课后练习
1．（北京海淀区）已知：如图，AB∥CD，CE平分∠ACD，∠A＝110°，则
∠ECD的度数等于（　　 ）
A、110°　　 B、70°　　 C、55°　　 D、35°
2．（福建福州）如图，已知：l1//l2，∠1=100°，则∠2= 　　 ．
3．（山西省）如图，直线a、b被直线c所截，且a//b，若∠1=118°，则∠2的度数为_________．
4．（龙岩市）如图AB∥CD，若∠ACD=69°，则∠CAB= __________
5．（苏州市）如图AB∥CD，直线EF分别交AB、CD于点E、F，ED平分∠BEF, 若∠1=72°，则∠2=_______
6．（仙桃市）如图直线L1∥L2、L3分别与L1，L2相交,则∠1与∠2的关系为（　 ）
　　A、∠1=∠2　　 B、∠1+∠2=180°　　 C、∠1+∠2=90°　　 D、∠1+∠2=360°
7．（镇江市）如图l1∥l2, ∠α是∠β的2倍, 则∠α等于 （　 ）
　　A：60°　　 B：90°　　 C：120°　　 D：150°
8．（临沂市）如图AB∥CD，那么∠1+∠2+∠3=（　 ）
　　A、180°　　 B、360°　　 C、540°　　 D、720°
9．（呼和浩特市）如图DE∥BC，EF∥AB，图中与∠BFE互补的角共有（　 ）
　　A、3个　　 B、2个　　 C、5个　　 D、4个
10.如图AB//CD,则的度数为
11.如图，己知AB//DE,,则__
12.如图，AB//CD,若,则 度.
13.如图试探索之间具备什么关系时，AB//CD,并说明理由。
A
B
C
D
E
F
1
2
3
4
A
E
G
B
C
F
H
D
A
D
E
B
C
1
2
A
D
F
B
E
C
1
2
3
A
D
B
E
C
F