3.8 弧长及扇形的面积培优精选试题(含解析)
文档属性
| 名称 | 3.8 弧长及扇形的面积培优精选试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-08 21:45:17 | ||
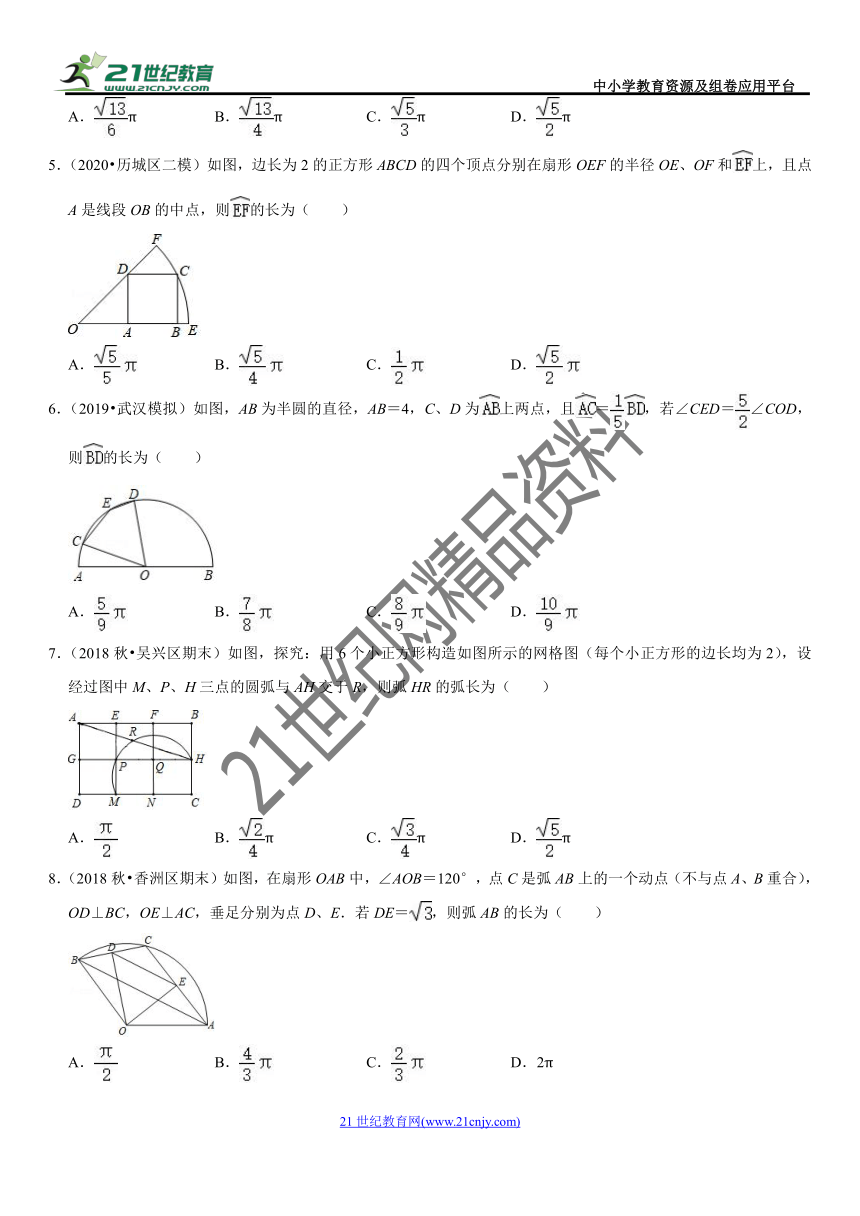
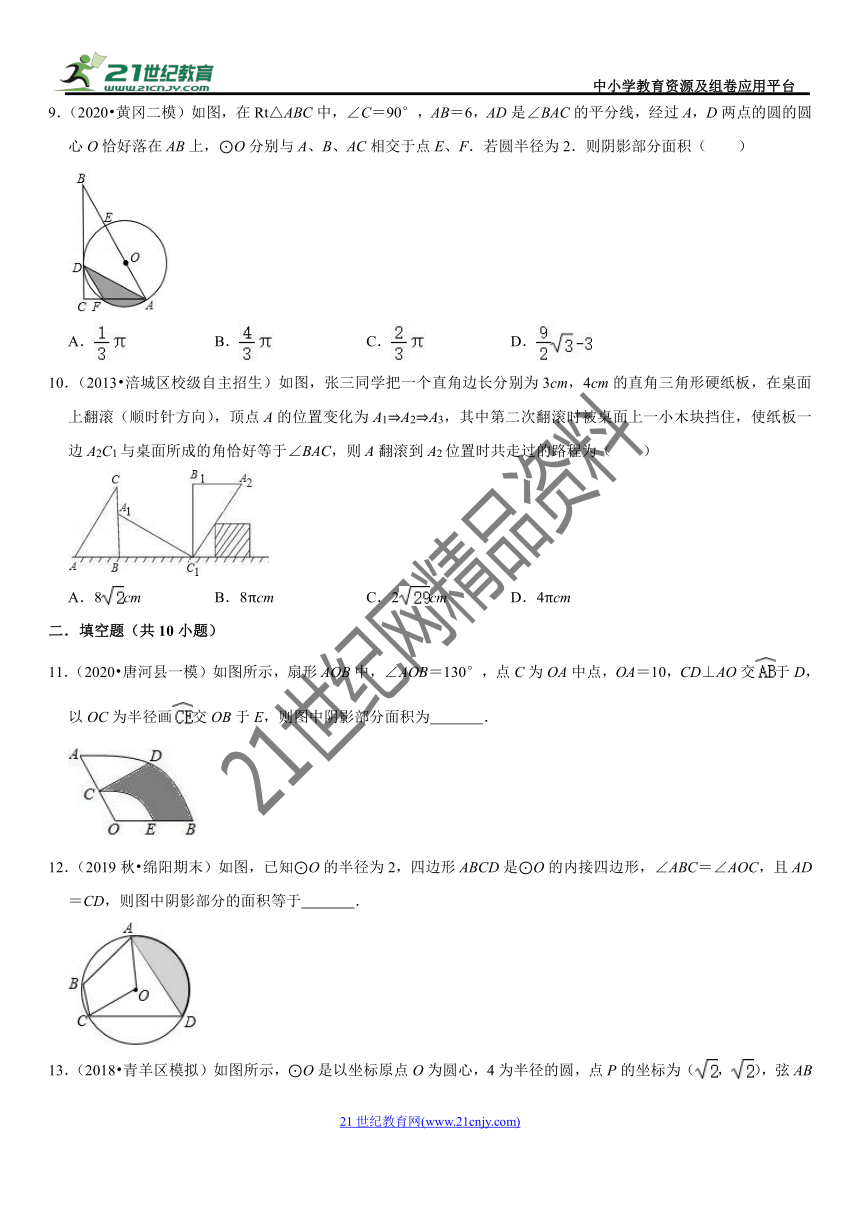
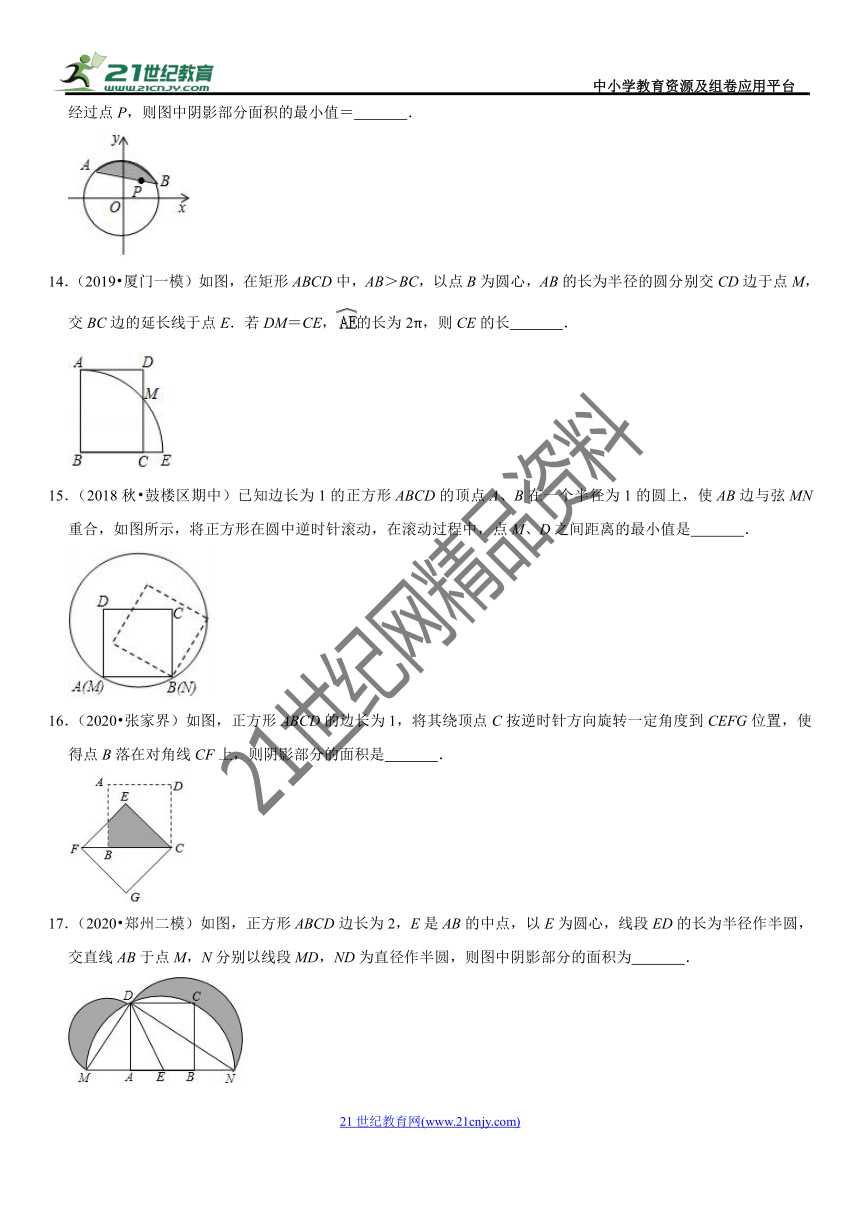
图片预览


文档简介
中小学教育资源及组卷应用平台
3.8弧长与面积公式小节习题精选(培优篇)
一.选择题(共10小题)
1.(2020?武汉模拟)如图,点A,B,C是⊙O上三点,AC=BC,点M为⊙O上一点,CE⊥AM,垂足为点E,AE=2,BM=,CM=,则的长为( )
A.π B.π C.π D.π
2.(2018?辉县市二模)如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧点D、E,则阴影部分的面积为( )
A.π﹣2 B.π+2 C.2﹣π D.+π
3.(2017?温州二模)如图,在△ABC中,∠C=90°,AB=,分别以A、B为圆心,AC,BC为半径在△ABC的外侧构造扇形CAE,扇形CBD,且点E,C,D在同一条直线上,若BC=2AC,且的长度恰好是的倍,则图中阴影部分的面积为( )
A.π B.π C.π D.π
4.(2020?镇海区模拟)如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于H,则弧AH的弧长为( )
A.π B.π C.π D.π
5.(2020?历城区二模)如图,边长为2的正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和上,且点A是线段OB的中点,则的长为( )
A. B. C. D.
6.(2019?武汉模拟)如图,AB为半圆的直径,AB=4,C、D为上两点,且=,若∠CED=∠COD,则的长为( )
A. B. C. D.
7.(2018秋?吴兴区期末)如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )
A. B.π C.π D.π
8.(2018秋?香洲区期末)如图,在扇形OAB中,∠AOB=120°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为点D、E.若DE=,则弧AB的长为( )
A. B. C. D.2π
9.(2020?黄冈二模)如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D两点的圆的圆心O恰好落在AB上,⊙O分别与A、B、AC相交于点E、F.若圆半径为2.则阴影部分面积( )
A. B. C. D.
10.(2013?涪城区校级自主招生)如图,张三同学把一个直角边长分别为3cm,4cm的直角三角形硬纸板,在桌面上翻滚(顺时针方向),顶点A的位置变化为A1?A2?A3,其中第二次翻滚时被桌面上一小木块挡住,使纸板一边A2C1与桌面所成的角恰好等于∠BAC,则A翻滚到A2位置时共走过的路程为( )
A.8cm B.8πcm C.2cm D.4πcm
二.填空题(共10小题)
11.(2020?唐河县一模)如图所示,扇形AOB中,∠AOB=130°,点C为OA中点,OA=10,CD⊥AO交于D,以OC为半径画交OB于E,则图中阴影部分面积为 .
12.(2019秋?绵阳期末)如图,已知⊙O的半径为2,四边形ABCD是⊙O的内接四边形,∠ABC=∠AOC,且AD=CD,则图中阴影部分的面积等于 .
13.(2018?青羊区模拟)如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为(,),弦AB经过点P,则图中阴影部分面积的最小值= .
14.(2019?厦门一模)如图,在矩形ABCD中,AB>BC,以点B为圆心,AB的长为半径的圆分别交CD边于点M,交BC边的延长线于点E.若DM=CE,的长为2π,则CE的长 .
15.(2018秋?鼓楼区期中)已知边长为1的正方形ABCD的顶点A、B在一个半径为1的圆上,使AB边与弦MN重合,如图所示,将正方形在圆中逆时针滚动,在滚动过程中,点M、D之间距离的最小值是 .
16.(2020?张家界)如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,则阴影部分的面积是 .
17.(2020?郑州二模)如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为 .
18.(2019秋?中山市期末)如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=,CD=2,则、和EF围成的阴影部分面积是 .
19.(2020?萧山区一模)如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是 .
20.(2020?铁西区二模)以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为 .
三.解答题(共10小题)
21.(2019秋?伊通县期末)如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
22.(2019?长春一模)如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接OD、DE.
(1)求证:OD⊥DE.
(2)若∠BAC=30°,AB=8,求阴影部分的面积.
23.(2019秋?曲阜市校级月考)如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?
24.(2017秋?嵊州市期末)如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
25.(2017秋?费县期末)如图,四边形ABCD内接于圆O,对角线AC是圆O的直径,DB平分∠ADC,AC长10cm.
(1)求点O到AB的距离;
(2)求阴影部分的面积.
26.(2017秋?鄞州区校级月考)如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
(1)求证:点C是劣弧的中点;
(2)如图②,连结EC,若AE=2AC=6,求阴影部分的面积.
27.(2017秋?东台市期中)如图,点P是正方形ABCD内一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置.
(1)设AB=m,PB=n(m>n),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
28.(2017?平邑县校级模拟)如图,菱形ABCO的顶点A的坐标为(﹣4,0),∠ABC=60°,将菱形ABCO绕点O顺时针旋转270°得到菱形A′B′C′O,图中阴影部分是菱形ABCO旋转时所扫过的面积,该圆弧与x轴的负半轴交于点M.
(1)求点C′的坐标和空白部分的∠AOC′的度数;
(2)试判断点M是否在A′B′所在的直线上,并说明理由;
(3)求图中阴影部分的面积.
29.(2016秋?鄱阳县校级期末)已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°得到△P'CB,若AB=m,PB=n(n<m).求△PAB旋转过程中边PA扫过区域(阴影部分)的面积;
(2)若PA=,PB=2,∠APB=135°,求PC的长.
3.8弧长与面积公式小节习题精选(培优篇)
参考答案与试题解析
一.选择题(共10小题)
1.(2020?武汉模拟)如图,点A,B,C是⊙O上三点,AC=BC,点M为⊙O上一点,CE⊥AM,垂足为点E,AE=2,BM=,CM=,则的长为( )
A.π B.π C.π D.π
【解答】解:在AE上截取AG=BM,连接CG,
∵AC=BC,∠A=∠B,
∴△ACG≌△BCM(SAS),
∴CG=CM=,
∵AE=2,AG=BM=,
∴GE=,
∵CE⊥AM,
∴CE===2,
∴tan∠A==,
∴∠A=30°,
∴∠COM=60°,
连接OM,CO,
∵OC=OM,
∴△COM是等边三角形,
∴OC=,
∴的长==,
故选:A.
2.(2018?辉县市二模)如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧点D、E,则阴影部分的面积为( )
A.π﹣2 B.π+2 C.2﹣π D.+π
【解答】解:连接OE,
∵∠BOA=90°,点C为BD的中点,CE∥OA,OA=4
∴∠ECO+∠COA=180°,OB=OE=4,OC=2,
∴∠OCE=90°,OE=2OC,
∴∠EOC=60°,CE=2,
∴阴影部分的面积为:=,
故选:A.
3.(2017?温州二模)如图,在△ABC中,∠C=90°,AB=,分别以A、B为圆心,AC,BC为半径在△ABC的外侧构造扇形CAE,扇形CBD,且点E,C,D在同一条直线上,若BC=2AC,且的长度恰好是的倍,则图中阴影部分的面积为( )
A.π B.π C.π D.π
【解答】解:如图,连接ED,作AM⊥EC于M,BN⊥CD于N.
∵BC=2AC,
∴设AC=x,BC=2x,
∵∠C=90°,
∴x2+(2x)2=5,
∴x=1,2x=2,
AC=1,BC=2,
∵∠AMC=∠BNC=∠ACB=90°,
∴∠ACM+∠CAM=90°,∠ACM+∠BCN=90°,
∴∠BCN=∠CAM,
∵∠CBN+∠BCN=90°,
∴∠CAM+∠CBN=90°,
∵AE=AC,AM⊥EC,BC=BD,BN⊥CD,
∴∠CAE=2∠CAM,∠CBD=2∠CBN,
∴∠CAE+∠CBD=180°,
∵的长度恰好是的倍,设∠CBD=m,∠CAE=n,
∴=×,
∴4m=5n,
∵m+n=180°,
∴m=100°,n=80°,
∴S阴=+=,
故选:B.
4.(2020?镇海区模拟)如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于H,则弧AH的弧长为( )
A.π B.π C.π D.π
【解答】解:连接EB,BH,AB,
∵BE=AB==,AE==,
∴BE2+AB2=AE2,
∴∠ABE=90°,
∴△ABE是等腰直角三角形,
∵∠ACB=90°,
∴AB是圆的直径,
∴∠AHB=90°,
∴BH⊥AH,
∴∠ABH=∠BAH=45°,
∴弧AH所对的圆心角为90°,
∴的长==.
故选:B.
5.(2020?历城区二模)如图,边长为2的正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和上,且点A是线段OB的中点,则的长为( )
A. B. C. D.
【解答】解:连接OC,
∵四边形ABCD是正方形,
∴AD=AB=BC=2,∠ABC=∠DAB=90°=∠DAO,
∵A为OB的中点,
∴OB=2AB=4,
在Rt△OBC中,由勾股定理得:OC===2,
∵A为OB的中点,AB=AD=2,
∴OA=AD=2,
∵∠DAO=90°,
∴∠DOA=∠ADO=45°,
∴的长为=π,
故选:D.
6.(2019?武汉模拟)如图,AB为半圆的直径,AB=4,C、D为上两点,且=,若∠CED=∠COD,则的长为( )
A. B. C. D.
【解答】解:设的度数为x°,则∠AOC=x,∠BOD=5x,∠COD=180°﹣6x,
∵∠CED=∠COD,
∴∠CED=(180°﹣6x),
∵∠CED+∠COD=180°,
∴(180°﹣6x)+90°﹣3x=180°,
解得x=20,
∴∠DOB=100°,
∴的长==π,
故选:D.
7.(2018秋?吴兴区期末)如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )
A. B.π C.π D.π
【解答】解:连接AM,MH,MR.
∵AM=MH=2,AH=2,
∴AM2+MH2=AH2,
∴∠AMH=90°,
∴△AMH是等腰直角三角形,
∵∠MPH=90°,
∴MH是圆的直径,
∴∠MRH=90°,
∴MR⊥AH,
∴∠RMH=∠RMA=45°,
∴弧RH所对的圆心角为90°,
∴的长==.
故选:D.
8.(2018秋?香洲区期末)如图,在扇形OAB中,∠AOB=120°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为点D、E.若DE=,则弧AB的长为( )
A. B. C. D.2π
【解答】解:如图作OH⊥AB于H.
∵OD⊥BC,OE⊥AC,
∴CD=DB,CE=AE,
∴AB=2DE=2,
∵OH⊥AB,
∴BH=AH=,
∵OA=OB,
∴∠AOH=∠BOH=60°,
OB==2,
∴的长==,
故选:B.
9.(2020?黄冈二模)如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D两点的圆的圆心O恰好落在AB上,⊙O分别与A、B、AC相交于点E、F.若圆半径为2.则阴影部分面积( )
A. B. C. D.
【解答】解:连接OD,OF.
∵AD是∠BAC的平分线,
∴∠DAB=∠DAC,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠ODA=∠DAC,
∴OD∥AC,
∴∠ODB=∠C=90°,
∴S△AFD=S△OFA,
∴S阴=S扇形OFA,
∵OD=OA=2,AB=6,
∴OB=4,
∴OB=2OD,
∴∠B=30°,
∴∠A=60°,
∵OF=OA,
∴△AOF是等边三角形,
∴∠AOF=60°,
∴S阴=S扇形OFA==.
故选:C.
10.(2013?涪城区校级自主招生)如图,张三同学把一个直角边长分别为3cm,4cm的直角三角形硬纸板,在桌面上翻滚(顺时针方向),顶点A的位置变化为A1?A2?A3,其中第二次翻滚时被桌面上一小木块挡住,使纸板一边A2C1与桌面所成的角恰好等于∠BAC,则A翻滚到A2位置时共走过的路程为( )
A.8cm B.8πcm C.2cm D.4πcm
【解答】解:根据题意得:=4πcm,
故选:D.
二.填空题(共10小题)
11.(2020?唐河县一模)如图所示,扇形AOB中,∠AOB=130°,点C为OA中点,OA=10,CD⊥AO交于D,以OC为半径画交OB于E,则图中阴影部分面积为 + .
【解答】解:如图,连接OD.
∵CD⊥OA,AC=OC,
∴OAO=2OC,
∴∠CDO=30°,
∴∠COD=60°,
∴S阴=S扇形OAB﹣S扇形OCE﹣(S扇形OAD﹣S△OCD)
=﹣﹣(﹣×5×5)
=+,
故答案为:+.
12.(2019秋?绵阳期末)如图,已知⊙O的半径为2,四边形ABCD是⊙O的内接四边形,∠ABC=∠AOC,且AD=CD,则图中阴影部分的面积等于 .
【解答】解:连接AC,OD,过点O作OE⊥AD,垂足为E,
∵∠ABC=∠AOC,∠AOC=2∠ADC,∠ABC+∠ADC=180°,
∴∠ABC=120°,∠ADC=60°,
∵AD=CD,
∴△ACD是正三角形,
∴∠AOD=120°,OE=2×cos60°=1,AD=2×sin60°×2=2,
∴S阴影部分=S扇形OAD﹣S△AOD=×π×22﹣×2×1=π﹣,
故答案为:π﹣.
13.(2018?青羊区模拟)如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为(,),弦AB经过点P,则图中阴影部分面积的最小值= .
【解答】解:由题意当OP⊥A'B'时,阴影部分的面积最小,
∵P(,),
∴OP=2,∵OA'=OB'=4,
∴PA'=PB'=2,
∴tan∠A'OP=tan∠B'OP=,
∴∠A'OP=∠B'OP=60°,
∴∠A'OB'=120°,
∴S阴=S扇形OA'B'﹣S△A'OB'=,
故答案为:.
14.(2019?厦门一模)如图,在矩形ABCD中,AB>BC,以点B为圆心,AB的长为半径的圆分别交CD边于点M,交BC边的延长线于点E.若DM=CE,的长为2π,则CE的长 4﹣2 .
【解答】解:连接BM,则AB=BE=BM,设BM=R,
∵四边形ABCD是矩形,
∴AB=CD=BE,∠B=∠BCD=90°,
∵DM=VE,
∴CM=BC,
∵的长为2π,
∴=2π,
解得:R=4,
即BM=BE=CD=AB=4,
在Rt△BCM中,由勾股定理得:BC2+CM2=BM2,
BC=CM=2,
∴CE=4﹣2,
故答案为:4﹣2.
15.(2018秋?鼓楼区期中)已知边长为1的正方形ABCD的顶点A、B在一个半径为1的圆上,使AB边与弦MN重合,如图所示,将正方形在圆中逆时针滚动,在滚动过程中,点M、D之间距离的最小值是 2﹣ .
【解答】解:如图,点D的运动轨迹是图中的红线.
观察图象可知M、D之间的最小距离是线段AD′的长=AE﹣EF=2﹣,
故答案为2﹣.
16.(2020?张家界)如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,则阴影部分的面积是 .
【解答】解:方法一:正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,
∴EF=CE=1,
∴CF=,
∴BF=﹣1,
∵∠BFE=45°,
∴阴影部分的面积=×1×1﹣×(﹣1)2=﹣1;
方法二:∵过E点作MN∥BC交AB、CD于M、N点,设AB与EF交于点P点,连接CP,如下图所示,
∵B在对角线CF上,
∴∠DCE=∠ECF=45°,EC=1,
∴△ENC为等腰直角三角形,
∴MB=CN=EC=,
又BC=AD=CD=CE,且CP=CP,△PEC和△PBC均为直角三角形,
∴Rt△PEC≌Rt△PBC(HL),
∴PB=PE,
又∠PFB=45°,
∴∠FPB=45°=∠MPE,
∴△MPE为等腰直角三角形,
设MP=x,则EP=BP=,
∵MP+BP=MB,
∴,解得,
∴BP=,
∴阴影部分的面积=.
故答案为:.
17.(2020?郑州二模)如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为 2 .
【解答】解:∵正方形ABCD边长为2,E是AB的中点,
∴∠DAE=90°,AE=1,AD=2,
∴DE=,
∴AN=AE+EN=1+,AM=﹣1,
∴MD==,ND==,
∴阴影部分的面积是:+﹣=2,
故答案为:2.
18.(2019秋?中山市期末)如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=,CD=2,则、和EF围成的阴影部分面积是 π+1﹣2 .
【解答】解:如图,连接EC.
∵四边形ABCD是矩形,
∴AD=BC=,CD=AB=EC=2,∠B=∠A=∠DCB=90°,
∴BE===,
∴BC=BE=,
∴∠BEC=∠BCE=45°,
∴∠ECD=45°,
∴S阴=S矩形ABCD﹣(S矩形ABCD﹣S扇形ADF)﹣(S矩形ABCD﹣S扇形CDE﹣S△EBC)
=S扇形ADF+S扇形CDE+S△EBC﹣S矩形ABCD
=++××﹣2×,
=π+1﹣2.
故答案为:π+1﹣2.
19.(2020?萧山区一模)如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是 ﹣ .
【解答】解:作EF⊥CD于F,
由旋转变换的性质可知,EF=BC=1,CD=CB+BD=4,
由勾股定理得,CA===,
则图中阴影部分的面积=△ABC的面积+扇形ABD的面积+△ECD的面积﹣扇形ACE的面积
=×1×3++﹣
=﹣,
故答案为:﹣.
20.(2020?铁西区二模)以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为 π﹣36 .
【解答】解:π×92+π×42﹣9×4
=π+π﹣36
=π﹣36.
答:图中阴影部分的面积为π﹣36.
故答案为:π﹣36.
三.解答题(共10小题)
21.(2019秋?伊通县期末)如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
【解答】(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O时AB的中点,
∴S△POB=S△PAB=×AP?PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
22.(2019?长春一模)如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接OD、DE.
(1)求证:OD⊥DE.
(2)若∠BAC=30°,AB=8,求阴影部分的面积.
【解答】(1)证明:连接DB.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°,
∵点E是BC的中点,
∴DE=CE=BC,
∴∠EDC=∠C,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠A+∠C=90°,
∴∠ADO+∠EDC=90°,
∴∠ODE=90°,
∴OD⊥DE;
(2)∵AB=8,∠BAC=30°,
∴AD=4,
阴影部分的面积=﹣×4×2
=π﹣4.
23.(2019秋?曲阜市校级月考)如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?
【解答】解:由图可得,5个扇形的圆心角之和为:(5﹣2)×180°=540°,
则五个阴影部分的面积之和==6π.
24.(2017秋?嵊州市期末)如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
【解答】(1)证明:连接OD,OC,
∵C、D是半圆O上的三等分点,
∴==,度数都是60°,
∴∠AOD=∠DOC=∠COB=60°,
∴∠DAC=30°,∠CAB=30°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠ADE=180°﹣90°﹣30°﹣30°=30°,
∴∠DAC∠ADE=30°,
∴AF=DF;
(2)解:由(1)知,∠AOD=60°,
∵OA=OD,AB=4,
∴△AOD是等边三角形,OA=2,
∵DE⊥AO,
∴DE=,
∴S阴影=S扇形AOD﹣S△AOD=﹣×2×=π﹣.
25.(2017秋?费县期末)如图,四边形ABCD内接于圆O,对角线AC是圆O的直径,DB平分∠ADC,AC长10cm.
(1)求点O到AB的距离;
(2)求阴影部分的面积.
【解答】解:(1)过点O作OE⊥AB于点E,
∵对角线AC是圆O的直径,DB平分∠ADC,
∴∠ADC=90°,则∠ADB=∠CDB=45°,
∴∠AOB=90°,
∵AO=BO,
∴△AOB是等腰直角三角形,
则EO=AO?sin45°=5×=(cm);
(2)阴影部分的面积为:﹣×5×5=﹣.
26.(2017秋?鄞州区校级月考)如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
(1)求证:点C是劣弧的中点;
(2)如图②,连结EC,若AE=2AC=6,求阴影部分的面积.
【解答】解:(1)连接CE,
∵AE是⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴AE=ED,
∴∠AEC=∠DEC,
∴=;
∴点C是劣弧 的中点;
(2)连接BC,OB,OC,
∵AE=2AC=6,
∴∠AEC=30°,AE=AD,
∴∠AED=60°,
∴△AED是等边三角形,
∴∠A=60°,
∵=,
∴==,
∴AE∥BC,∠BOC=60°,
∴S△OBC=S△EBC,
∴S阴影=S扇形==π.
27.(2017秋?东台市期中)如图,点P是正方形ABCD内一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置.
(1)设AB=m,PB=n(m>n),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
【解答】解:
(1)∵将△PAB绕点B顺时针旋转90°到△P′CB的位置,
∴△PAB≌△P'CB,
∴S△PAB=S△P'CB,S阴影=S扇形BAC﹣S扇形BPP′=(m2﹣n2);
(2)连接PP′,根据旋转的性质可知:△APB≌△CP′B,
∴BP=BP′=4,P′C=PA=2,∠PBP′=90°,
∴△PBP'是等腰直角三角形,P′P2=PB2+P'B2=32.
又∵∠BP′C=∠BPA=135°,
∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣45°=90°,
即△PP′C是直角三角形,
∴PC==6.
28.(2017?平邑县校级模拟)如图,菱形ABCO的顶点A的坐标为(﹣4,0),∠ABC=60°,将菱形ABCO绕点O顺时针旋转270°得到菱形A′B′C′O,图中阴影部分是菱形ABCO旋转时所扫过的面积,该圆弧与x轴的负半轴交于点M.
(1)求点C′的坐标和空白部分的∠AOC′的度数;
(2)试判断点M是否在A′B′所在的直线上,并说明理由;
(3)求图中阴影部分的面积.
【解答】解:(1)∵菱形ABCO的顶点A的坐标为(﹣4,0),∠ABC=60°,
∴∠AOC=60°,
∴∠COA′=30°,
∴∠A′OC′=60°,
∴点C′的横坐标是:4×sin60°=2,纵坐标是:﹣4×cos60°=﹣2,
∴点C′的坐标是(2,﹣2),
由题意可得,∠AOC′=∠AOA′+∠A′OC′=90°+60°=150°,
即点C′的坐标是(2,﹣2),∠AOC′=150°;
(2)点M在点A′、B′所在的直线上,
理由:由题意可得,
点A′的坐标是(0,﹣4),
点B′的横坐标是:4×sin60°=2,纵坐标是:﹣4+(﹣4×cos60°)=﹣6,
即点B′的坐标是(2,﹣6),
设过点A′、B′所在的直线的解析式为y=kx+b,
,得,
∴过点A′、B′所在的直线的解析式为y=,
∵OB的长度为:,
∴点M的坐标为(﹣,0),
将x=﹣4代入y=,得y=0,
∴点M在点A′、B′所在的直线上;
(3)∵OB的长度为4,OA=4,
∴阴影部分的面积是:﹣=36π﹣.
29.(2016秋?鄱阳县校级期末)已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°得到△P'CB,若AB=m,PB=n(n<m).求△PAB旋转过程中边PA扫过区域(阴影部分)的面积;
(2)若PA=,PB=2,∠APB=135°,求PC的长.
【解答】解:(1)由旋转的性质可知,S△ABP=S△CBP′,
∴△PAB旋转过程中边PA扫过区域面积=﹣=(m2﹣n2);
(2)连接PP′,
由旋转的性质可知,∠BP′C=∠APB=135°,∠PBP′=90°,BP′=BP=2,P′C=PA=,
∴PP′==4,∠PP′C=90°,
∴PC==3.
明: 属1所有,未经书面同意,不得复制发日期:2020/8/2 20:36:54;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
3.8弧长与面积公式小节习题精选(培优篇)
一.选择题(共10小题)
1.(2020?武汉模拟)如图,点A,B,C是⊙O上三点,AC=BC,点M为⊙O上一点,CE⊥AM,垂足为点E,AE=2,BM=,CM=,则的长为( )
A.π B.π C.π D.π
2.(2018?辉县市二模)如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧点D、E,则阴影部分的面积为( )
A.π﹣2 B.π+2 C.2﹣π D.+π
3.(2017?温州二模)如图,在△ABC中,∠C=90°,AB=,分别以A、B为圆心,AC,BC为半径在△ABC的外侧构造扇形CAE,扇形CBD,且点E,C,D在同一条直线上,若BC=2AC,且的长度恰好是的倍,则图中阴影部分的面积为( )
A.π B.π C.π D.π
4.(2020?镇海区模拟)如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于H,则弧AH的弧长为( )
A.π B.π C.π D.π
5.(2020?历城区二模)如图,边长为2的正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和上,且点A是线段OB的中点,则的长为( )
A. B. C. D.
6.(2019?武汉模拟)如图,AB为半圆的直径,AB=4,C、D为上两点,且=,若∠CED=∠COD,则的长为( )
A. B. C. D.
7.(2018秋?吴兴区期末)如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )
A. B.π C.π D.π
8.(2018秋?香洲区期末)如图,在扇形OAB中,∠AOB=120°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为点D、E.若DE=,则弧AB的长为( )
A. B. C. D.2π
9.(2020?黄冈二模)如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D两点的圆的圆心O恰好落在AB上,⊙O分别与A、B、AC相交于点E、F.若圆半径为2.则阴影部分面积( )
A. B. C. D.
10.(2013?涪城区校级自主招生)如图,张三同学把一个直角边长分别为3cm,4cm的直角三角形硬纸板,在桌面上翻滚(顺时针方向),顶点A的位置变化为A1?A2?A3,其中第二次翻滚时被桌面上一小木块挡住,使纸板一边A2C1与桌面所成的角恰好等于∠BAC,则A翻滚到A2位置时共走过的路程为( )
A.8cm B.8πcm C.2cm D.4πcm
二.填空题(共10小题)
11.(2020?唐河县一模)如图所示,扇形AOB中,∠AOB=130°,点C为OA中点,OA=10,CD⊥AO交于D,以OC为半径画交OB于E,则图中阴影部分面积为 .
12.(2019秋?绵阳期末)如图,已知⊙O的半径为2,四边形ABCD是⊙O的内接四边形,∠ABC=∠AOC,且AD=CD,则图中阴影部分的面积等于 .
13.(2018?青羊区模拟)如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为(,),弦AB经过点P,则图中阴影部分面积的最小值= .
14.(2019?厦门一模)如图,在矩形ABCD中,AB>BC,以点B为圆心,AB的长为半径的圆分别交CD边于点M,交BC边的延长线于点E.若DM=CE,的长为2π,则CE的长 .
15.(2018秋?鼓楼区期中)已知边长为1的正方形ABCD的顶点A、B在一个半径为1的圆上,使AB边与弦MN重合,如图所示,将正方形在圆中逆时针滚动,在滚动过程中,点M、D之间距离的最小值是 .
16.(2020?张家界)如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,则阴影部分的面积是 .
17.(2020?郑州二模)如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为 .
18.(2019秋?中山市期末)如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=,CD=2,则、和EF围成的阴影部分面积是 .
19.(2020?萧山区一模)如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是 .
20.(2020?铁西区二模)以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为 .
三.解答题(共10小题)
21.(2019秋?伊通县期末)如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
22.(2019?长春一模)如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接OD、DE.
(1)求证:OD⊥DE.
(2)若∠BAC=30°,AB=8,求阴影部分的面积.
23.(2019秋?曲阜市校级月考)如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?
24.(2017秋?嵊州市期末)如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
25.(2017秋?费县期末)如图,四边形ABCD内接于圆O,对角线AC是圆O的直径,DB平分∠ADC,AC长10cm.
(1)求点O到AB的距离;
(2)求阴影部分的面积.
26.(2017秋?鄞州区校级月考)如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
(1)求证:点C是劣弧的中点;
(2)如图②,连结EC,若AE=2AC=6,求阴影部分的面积.
27.(2017秋?东台市期中)如图,点P是正方形ABCD内一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置.
(1)设AB=m,PB=n(m>n),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
28.(2017?平邑县校级模拟)如图,菱形ABCO的顶点A的坐标为(﹣4,0),∠ABC=60°,将菱形ABCO绕点O顺时针旋转270°得到菱形A′B′C′O,图中阴影部分是菱形ABCO旋转时所扫过的面积,该圆弧与x轴的负半轴交于点M.
(1)求点C′的坐标和空白部分的∠AOC′的度数;
(2)试判断点M是否在A′B′所在的直线上,并说明理由;
(3)求图中阴影部分的面积.
29.(2016秋?鄱阳县校级期末)已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°得到△P'CB,若AB=m,PB=n(n<m).求△PAB旋转过程中边PA扫过区域(阴影部分)的面积;
(2)若PA=,PB=2,∠APB=135°,求PC的长.
3.8弧长与面积公式小节习题精选(培优篇)
参考答案与试题解析
一.选择题(共10小题)
1.(2020?武汉模拟)如图,点A,B,C是⊙O上三点,AC=BC,点M为⊙O上一点,CE⊥AM,垂足为点E,AE=2,BM=,CM=,则的长为( )
A.π B.π C.π D.π
【解答】解:在AE上截取AG=BM,连接CG,
∵AC=BC,∠A=∠B,
∴△ACG≌△BCM(SAS),
∴CG=CM=,
∵AE=2,AG=BM=,
∴GE=,
∵CE⊥AM,
∴CE===2,
∴tan∠A==,
∴∠A=30°,
∴∠COM=60°,
连接OM,CO,
∵OC=OM,
∴△COM是等边三角形,
∴OC=,
∴的长==,
故选:A.
2.(2018?辉县市二模)如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧点D、E,则阴影部分的面积为( )
A.π﹣2 B.π+2 C.2﹣π D.+π
【解答】解:连接OE,
∵∠BOA=90°,点C为BD的中点,CE∥OA,OA=4
∴∠ECO+∠COA=180°,OB=OE=4,OC=2,
∴∠OCE=90°,OE=2OC,
∴∠EOC=60°,CE=2,
∴阴影部分的面积为:=,
故选:A.
3.(2017?温州二模)如图,在△ABC中,∠C=90°,AB=,分别以A、B为圆心,AC,BC为半径在△ABC的外侧构造扇形CAE,扇形CBD,且点E,C,D在同一条直线上,若BC=2AC,且的长度恰好是的倍,则图中阴影部分的面积为( )
A.π B.π C.π D.π
【解答】解:如图,连接ED,作AM⊥EC于M,BN⊥CD于N.
∵BC=2AC,
∴设AC=x,BC=2x,
∵∠C=90°,
∴x2+(2x)2=5,
∴x=1,2x=2,
AC=1,BC=2,
∵∠AMC=∠BNC=∠ACB=90°,
∴∠ACM+∠CAM=90°,∠ACM+∠BCN=90°,
∴∠BCN=∠CAM,
∵∠CBN+∠BCN=90°,
∴∠CAM+∠CBN=90°,
∵AE=AC,AM⊥EC,BC=BD,BN⊥CD,
∴∠CAE=2∠CAM,∠CBD=2∠CBN,
∴∠CAE+∠CBD=180°,
∵的长度恰好是的倍,设∠CBD=m,∠CAE=n,
∴=×,
∴4m=5n,
∵m+n=180°,
∴m=100°,n=80°,
∴S阴=+=,
故选:B.
4.(2020?镇海区模拟)如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于H,则弧AH的弧长为( )
A.π B.π C.π D.π
【解答】解:连接EB,BH,AB,
∵BE=AB==,AE==,
∴BE2+AB2=AE2,
∴∠ABE=90°,
∴△ABE是等腰直角三角形,
∵∠ACB=90°,
∴AB是圆的直径,
∴∠AHB=90°,
∴BH⊥AH,
∴∠ABH=∠BAH=45°,
∴弧AH所对的圆心角为90°,
∴的长==.
故选:B.
5.(2020?历城区二模)如图,边长为2的正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和上,且点A是线段OB的中点,则的长为( )
A. B. C. D.
【解答】解:连接OC,
∵四边形ABCD是正方形,
∴AD=AB=BC=2,∠ABC=∠DAB=90°=∠DAO,
∵A为OB的中点,
∴OB=2AB=4,
在Rt△OBC中,由勾股定理得:OC===2,
∵A为OB的中点,AB=AD=2,
∴OA=AD=2,
∵∠DAO=90°,
∴∠DOA=∠ADO=45°,
∴的长为=π,
故选:D.
6.(2019?武汉模拟)如图,AB为半圆的直径,AB=4,C、D为上两点,且=,若∠CED=∠COD,则的长为( )
A. B. C. D.
【解答】解:设的度数为x°,则∠AOC=x,∠BOD=5x,∠COD=180°﹣6x,
∵∠CED=∠COD,
∴∠CED=(180°﹣6x),
∵∠CED+∠COD=180°,
∴(180°﹣6x)+90°﹣3x=180°,
解得x=20,
∴∠DOB=100°,
∴的长==π,
故选:D.
7.(2018秋?吴兴区期末)如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )
A. B.π C.π D.π
【解答】解:连接AM,MH,MR.
∵AM=MH=2,AH=2,
∴AM2+MH2=AH2,
∴∠AMH=90°,
∴△AMH是等腰直角三角形,
∵∠MPH=90°,
∴MH是圆的直径,
∴∠MRH=90°,
∴MR⊥AH,
∴∠RMH=∠RMA=45°,
∴弧RH所对的圆心角为90°,
∴的长==.
故选:D.
8.(2018秋?香洲区期末)如图,在扇形OAB中,∠AOB=120°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为点D、E.若DE=,则弧AB的长为( )
A. B. C. D.2π
【解答】解:如图作OH⊥AB于H.
∵OD⊥BC,OE⊥AC,
∴CD=DB,CE=AE,
∴AB=2DE=2,
∵OH⊥AB,
∴BH=AH=,
∵OA=OB,
∴∠AOH=∠BOH=60°,
OB==2,
∴的长==,
故选:B.
9.(2020?黄冈二模)如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D两点的圆的圆心O恰好落在AB上,⊙O分别与A、B、AC相交于点E、F.若圆半径为2.则阴影部分面积( )
A. B. C. D.
【解答】解:连接OD,OF.
∵AD是∠BAC的平分线,
∴∠DAB=∠DAC,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠ODA=∠DAC,
∴OD∥AC,
∴∠ODB=∠C=90°,
∴S△AFD=S△OFA,
∴S阴=S扇形OFA,
∵OD=OA=2,AB=6,
∴OB=4,
∴OB=2OD,
∴∠B=30°,
∴∠A=60°,
∵OF=OA,
∴△AOF是等边三角形,
∴∠AOF=60°,
∴S阴=S扇形OFA==.
故选:C.
10.(2013?涪城区校级自主招生)如图,张三同学把一个直角边长分别为3cm,4cm的直角三角形硬纸板,在桌面上翻滚(顺时针方向),顶点A的位置变化为A1?A2?A3,其中第二次翻滚时被桌面上一小木块挡住,使纸板一边A2C1与桌面所成的角恰好等于∠BAC,则A翻滚到A2位置时共走过的路程为( )
A.8cm B.8πcm C.2cm D.4πcm
【解答】解:根据题意得:=4πcm,
故选:D.
二.填空题(共10小题)
11.(2020?唐河县一模)如图所示,扇形AOB中,∠AOB=130°,点C为OA中点,OA=10,CD⊥AO交于D,以OC为半径画交OB于E,则图中阴影部分面积为 + .
【解答】解:如图,连接OD.
∵CD⊥OA,AC=OC,
∴OAO=2OC,
∴∠CDO=30°,
∴∠COD=60°,
∴S阴=S扇形OAB﹣S扇形OCE﹣(S扇形OAD﹣S△OCD)
=﹣﹣(﹣×5×5)
=+,
故答案为:+.
12.(2019秋?绵阳期末)如图,已知⊙O的半径为2,四边形ABCD是⊙O的内接四边形,∠ABC=∠AOC,且AD=CD,则图中阴影部分的面积等于 .
【解答】解:连接AC,OD,过点O作OE⊥AD,垂足为E,
∵∠ABC=∠AOC,∠AOC=2∠ADC,∠ABC+∠ADC=180°,
∴∠ABC=120°,∠ADC=60°,
∵AD=CD,
∴△ACD是正三角形,
∴∠AOD=120°,OE=2×cos60°=1,AD=2×sin60°×2=2,
∴S阴影部分=S扇形OAD﹣S△AOD=×π×22﹣×2×1=π﹣,
故答案为:π﹣.
13.(2018?青羊区模拟)如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为(,),弦AB经过点P,则图中阴影部分面积的最小值= .
【解答】解:由题意当OP⊥A'B'时,阴影部分的面积最小,
∵P(,),
∴OP=2,∵OA'=OB'=4,
∴PA'=PB'=2,
∴tan∠A'OP=tan∠B'OP=,
∴∠A'OP=∠B'OP=60°,
∴∠A'OB'=120°,
∴S阴=S扇形OA'B'﹣S△A'OB'=,
故答案为:.
14.(2019?厦门一模)如图,在矩形ABCD中,AB>BC,以点B为圆心,AB的长为半径的圆分别交CD边于点M,交BC边的延长线于点E.若DM=CE,的长为2π,则CE的长 4﹣2 .
【解答】解:连接BM,则AB=BE=BM,设BM=R,
∵四边形ABCD是矩形,
∴AB=CD=BE,∠B=∠BCD=90°,
∵DM=VE,
∴CM=BC,
∵的长为2π,
∴=2π,
解得:R=4,
即BM=BE=CD=AB=4,
在Rt△BCM中,由勾股定理得:BC2+CM2=BM2,
BC=CM=2,
∴CE=4﹣2,
故答案为:4﹣2.
15.(2018秋?鼓楼区期中)已知边长为1的正方形ABCD的顶点A、B在一个半径为1的圆上,使AB边与弦MN重合,如图所示,将正方形在圆中逆时针滚动,在滚动过程中,点M、D之间距离的最小值是 2﹣ .
【解答】解:如图,点D的运动轨迹是图中的红线.
观察图象可知M、D之间的最小距离是线段AD′的长=AE﹣EF=2﹣,
故答案为2﹣.
16.(2020?张家界)如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,则阴影部分的面积是 .
【解答】解:方法一:正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,
∴EF=CE=1,
∴CF=,
∴BF=﹣1,
∵∠BFE=45°,
∴阴影部分的面积=×1×1﹣×(﹣1)2=﹣1;
方法二:∵过E点作MN∥BC交AB、CD于M、N点,设AB与EF交于点P点,连接CP,如下图所示,
∵B在对角线CF上,
∴∠DCE=∠ECF=45°,EC=1,
∴△ENC为等腰直角三角形,
∴MB=CN=EC=,
又BC=AD=CD=CE,且CP=CP,△PEC和△PBC均为直角三角形,
∴Rt△PEC≌Rt△PBC(HL),
∴PB=PE,
又∠PFB=45°,
∴∠FPB=45°=∠MPE,
∴△MPE为等腰直角三角形,
设MP=x,则EP=BP=,
∵MP+BP=MB,
∴,解得,
∴BP=,
∴阴影部分的面积=.
故答案为:.
17.(2020?郑州二模)如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为 2 .
【解答】解:∵正方形ABCD边长为2,E是AB的中点,
∴∠DAE=90°,AE=1,AD=2,
∴DE=,
∴AN=AE+EN=1+,AM=﹣1,
∴MD==,ND==,
∴阴影部分的面积是:+﹣=2,
故答案为:2.
18.(2019秋?中山市期末)如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=,CD=2,则、和EF围成的阴影部分面积是 π+1﹣2 .
【解答】解:如图,连接EC.
∵四边形ABCD是矩形,
∴AD=BC=,CD=AB=EC=2,∠B=∠A=∠DCB=90°,
∴BE===,
∴BC=BE=,
∴∠BEC=∠BCE=45°,
∴∠ECD=45°,
∴S阴=S矩形ABCD﹣(S矩形ABCD﹣S扇形ADF)﹣(S矩形ABCD﹣S扇形CDE﹣S△EBC)
=S扇形ADF+S扇形CDE+S△EBC﹣S矩形ABCD
=++××﹣2×,
=π+1﹣2.
故答案为:π+1﹣2.
19.(2020?萧山区一模)如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是 ﹣ .
【解答】解:作EF⊥CD于F,
由旋转变换的性质可知,EF=BC=1,CD=CB+BD=4,
由勾股定理得,CA===,
则图中阴影部分的面积=△ABC的面积+扇形ABD的面积+△ECD的面积﹣扇形ACE的面积
=×1×3++﹣
=﹣,
故答案为:﹣.
20.(2020?铁西区二模)以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为 π﹣36 .
【解答】解:π×92+π×42﹣9×4
=π+π﹣36
=π﹣36.
答:图中阴影部分的面积为π﹣36.
故答案为:π﹣36.
三.解答题(共10小题)
21.(2019秋?伊通县期末)如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
【解答】(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O时AB的中点,
∴S△POB=S△PAB=×AP?PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
22.(2019?长春一模)如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接OD、DE.
(1)求证:OD⊥DE.
(2)若∠BAC=30°,AB=8,求阴影部分的面积.
【解答】(1)证明:连接DB.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°,
∵点E是BC的中点,
∴DE=CE=BC,
∴∠EDC=∠C,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠A+∠C=90°,
∴∠ADO+∠EDC=90°,
∴∠ODE=90°,
∴OD⊥DE;
(2)∵AB=8,∠BAC=30°,
∴AD=4,
阴影部分的面积=﹣×4×2
=π﹣4.
23.(2019秋?曲阜市校级月考)如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?
【解答】解:由图可得,5个扇形的圆心角之和为:(5﹣2)×180°=540°,
则五个阴影部分的面积之和==6π.
24.(2017秋?嵊州市期末)如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
【解答】(1)证明:连接OD,OC,
∵C、D是半圆O上的三等分点,
∴==,度数都是60°,
∴∠AOD=∠DOC=∠COB=60°,
∴∠DAC=30°,∠CAB=30°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠ADE=180°﹣90°﹣30°﹣30°=30°,
∴∠DAC∠ADE=30°,
∴AF=DF;
(2)解:由(1)知,∠AOD=60°,
∵OA=OD,AB=4,
∴△AOD是等边三角形,OA=2,
∵DE⊥AO,
∴DE=,
∴S阴影=S扇形AOD﹣S△AOD=﹣×2×=π﹣.
25.(2017秋?费县期末)如图,四边形ABCD内接于圆O,对角线AC是圆O的直径,DB平分∠ADC,AC长10cm.
(1)求点O到AB的距离;
(2)求阴影部分的面积.
【解答】解:(1)过点O作OE⊥AB于点E,
∵对角线AC是圆O的直径,DB平分∠ADC,
∴∠ADC=90°,则∠ADB=∠CDB=45°,
∴∠AOB=90°,
∵AO=BO,
∴△AOB是等腰直角三角形,
则EO=AO?sin45°=5×=(cm);
(2)阴影部分的面积为:﹣×5×5=﹣.
26.(2017秋?鄞州区校级月考)如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
(1)求证:点C是劣弧的中点;
(2)如图②,连结EC,若AE=2AC=6,求阴影部分的面积.
【解答】解:(1)连接CE,
∵AE是⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴AE=ED,
∴∠AEC=∠DEC,
∴=;
∴点C是劣弧 的中点;
(2)连接BC,OB,OC,
∵AE=2AC=6,
∴∠AEC=30°,AE=AD,
∴∠AED=60°,
∴△AED是等边三角形,
∴∠A=60°,
∵=,
∴==,
∴AE∥BC,∠BOC=60°,
∴S△OBC=S△EBC,
∴S阴影=S扇形==π.
27.(2017秋?东台市期中)如图,点P是正方形ABCD内一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置.
(1)设AB=m,PB=n(m>n),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
【解答】解:
(1)∵将△PAB绕点B顺时针旋转90°到△P′CB的位置,
∴△PAB≌△P'CB,
∴S△PAB=S△P'CB,S阴影=S扇形BAC﹣S扇形BPP′=(m2﹣n2);
(2)连接PP′,根据旋转的性质可知:△APB≌△CP′B,
∴BP=BP′=4,P′C=PA=2,∠PBP′=90°,
∴△PBP'是等腰直角三角形,P′P2=PB2+P'B2=32.
又∵∠BP′C=∠BPA=135°,
∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣45°=90°,
即△PP′C是直角三角形,
∴PC==6.
28.(2017?平邑县校级模拟)如图,菱形ABCO的顶点A的坐标为(﹣4,0),∠ABC=60°,将菱形ABCO绕点O顺时针旋转270°得到菱形A′B′C′O,图中阴影部分是菱形ABCO旋转时所扫过的面积,该圆弧与x轴的负半轴交于点M.
(1)求点C′的坐标和空白部分的∠AOC′的度数;
(2)试判断点M是否在A′B′所在的直线上,并说明理由;
(3)求图中阴影部分的面积.
【解答】解:(1)∵菱形ABCO的顶点A的坐标为(﹣4,0),∠ABC=60°,
∴∠AOC=60°,
∴∠COA′=30°,
∴∠A′OC′=60°,
∴点C′的横坐标是:4×sin60°=2,纵坐标是:﹣4×cos60°=﹣2,
∴点C′的坐标是(2,﹣2),
由题意可得,∠AOC′=∠AOA′+∠A′OC′=90°+60°=150°,
即点C′的坐标是(2,﹣2),∠AOC′=150°;
(2)点M在点A′、B′所在的直线上,
理由:由题意可得,
点A′的坐标是(0,﹣4),
点B′的横坐标是:4×sin60°=2,纵坐标是:﹣4+(﹣4×cos60°)=﹣6,
即点B′的坐标是(2,﹣6),
设过点A′、B′所在的直线的解析式为y=kx+b,
,得,
∴过点A′、B′所在的直线的解析式为y=,
∵OB的长度为:,
∴点M的坐标为(﹣,0),
将x=﹣4代入y=,得y=0,
∴点M在点A′、B′所在的直线上;
(3)∵OB的长度为4,OA=4,
∴阴影部分的面积是:﹣=36π﹣.
29.(2016秋?鄱阳县校级期末)已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°得到△P'CB,若AB=m,PB=n(n<m).求△PAB旋转过程中边PA扫过区域(阴影部分)的面积;
(2)若PA=,PB=2,∠APB=135°,求PC的长.
【解答】解:(1)由旋转的性质可知,S△ABP=S△CBP′,
∴△PAB旋转过程中边PA扫过区域面积=﹣=(m2﹣n2);
(2)连接PP′,
由旋转的性质可知,∠BP′C=∠APB=135°,∠PBP′=90°,BP′=BP=2,P′C=PA=,
∴PP′==4,∠PP′C=90°,
∴PC==3.
明: 属1所有,未经书面同意,不得复制发日期:2020/8/2 20:36:54;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
同课章节目录
