1.1.2从自然数到有理数 教学课件(共22张PPT)
文档属性
| 名称 | 1.1.2从自然数到有理数 教学课件(共22张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 15:18:51 | ||
图片预览






文档简介
(共22张PPT)
人教版
七上
1.1.2从自然数到有理数
知识回顾
1.自然数可以用来计数、测量、标号或排序;分数和小数在实际生活中的应用.
2.数的运算在人们分析、判断、解决实际问题过程中的重要作用
.
3.小学学过的数不够用了,数的范围需要扩展.
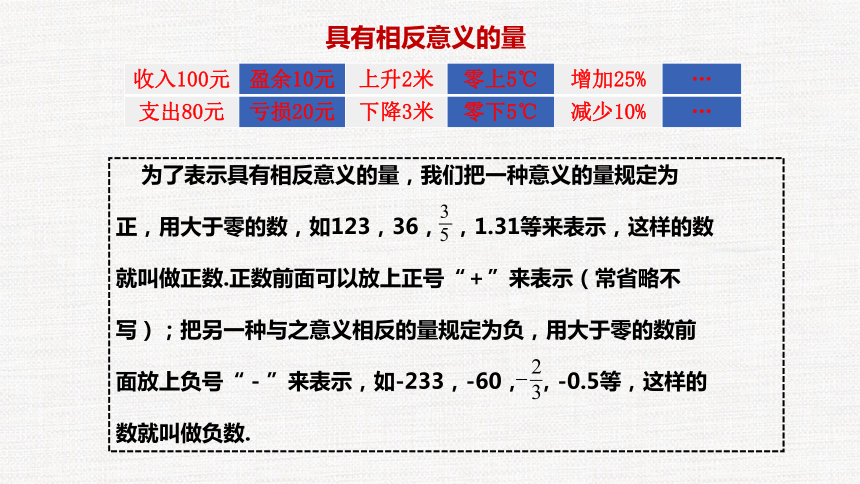
具有相反意义的量
收入100元
盈余10元
上升2米
零上5℃
增加25%
…
支出80元
亏损20元
下降3米
零下5℃
减少10%
…
为了表示具有相反意义的量,我们把一种意义的量规定为
正,用大于零的数,如123,36,
,1.31等来表示,这样的数
就叫做正数.正数前面可以放上正号“+”来表示(常省略不
写);把另一种与之意义相反的量规定为负,用大于零的数前
面放上负号“-”来表示,如-233,-60,
,-0.5等,这样的
数就叫做负数.
为了表示具有相反意义的量,我们把其中的一种意义的量规定为正,小学学过的数(零除外),如123,25,2.5等数叫做正数(positive
number).正数前面可以放上“+”号(常省略不写).
零既不是正数,也不是负数.
“-”不可以省略!
把另一种与之意义相反的量规定为负,在前面放上负
号“?”来表示,如?233,?60,-0.5等叫做负数
(negative
number).
注意
1.下列四个数中,正整数是( )
A.﹣2
B.﹣1
C.0
D.1
【分析】正整数是指既是正数还是整数,由此即可判定求解.
解:A、﹣2是负整数,故选项错误;
B、﹣1是负整数,故选项错误;
C、0是非正整数,故选项错误;
D、1是正整数,故选项正确.
故选D.
我们把1,2,3,4,…称为正整数;
-1,-2,-3,-4,…称为负整数;
,
,
,4.5,…称为正分数;
,
,
,-4.5,…称为负分数.
有理数的分类
知识小结
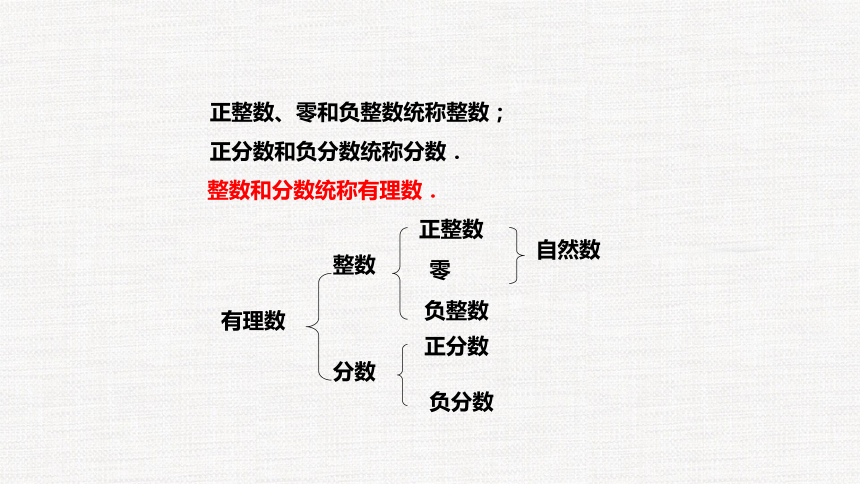
正整数、零和负整数统称整数;
整数和分数统称有理数.
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
正分数和负分数统称分数.
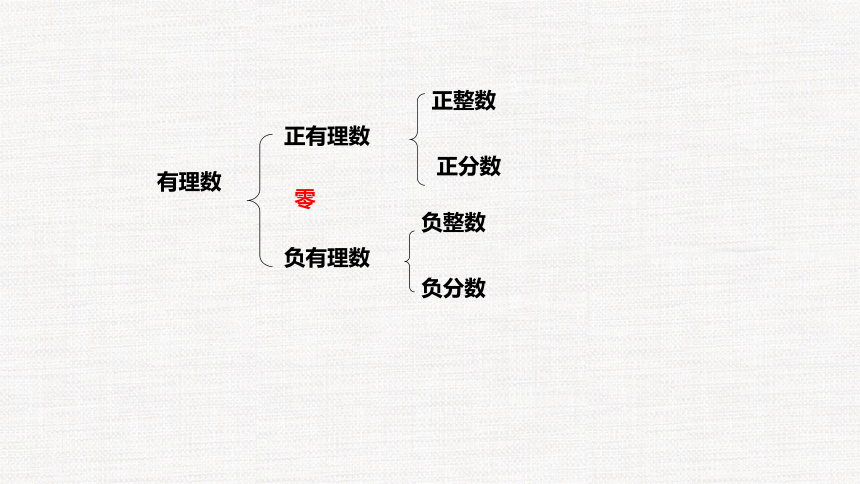
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
非负数是
,
非正数是
,
非负整数是
,
非正整数是
.
零和正数
零和正整数
零和负数
零和负整数
(1)零是______________________________;
(2)零不是_____________________________;
正数,
不是负数,
也不是分数
自然数,
是整数,
是有理数
合作探究
解:
22
,
,
0.33是正数;
-8.4
,
,
-9
是负数;
22
,
0,
-9
是整数;
以上所给各数均为有理数.
-8.4
,
,
0.33
,
是分数;
例
下列给出的各数,哪些是正数?哪些是负数?哪些是整数?哪些是分数?哪些是有理数?
-8.4,22,
,0.33,0,
,-9.
例题讲解
3.把下列各数分别填在相应的集合里:
-1,
,0.3,0,-1.7,21,-2,1.01001,+6.
(1)正数集合{
…}
(2)负数集合{
…}
(3)正整数集合{
…}
(4)分数集合{
…}.
解:(1)正数集合{
,0.3,21,1.01001,+6,…}
(2)负数集合{-1,-1.7,-2,…}
(3)正整数集合{21,+6,…}
(4)分数集合{
,0.3,-1.7,1.01001,…}
变式练习
(1)汽车在一条南北走向的高速公路上行驶,规定向北行驶的路程为正.汽车向北行驶75
km,记做______km(或____km),汽车向南行驶100km,记做________km;
(2)如果向银行存入50元记为50元,那么-30.50元表示______________________;
(3)规定增加的百分比为正,增加25%记做_______,-12%表示___________;
1、填空:
75
+75
-100
从银行取出30.50元
25%
减少12%
(4)规定温度零上为正,月球白天气温高达零上123℃
,记为__________,夜晚气温低至零下233
℃,记为________.阿波罗11号宇航员登上月球后不得不穿着御寒又防热的太空服.
+123℃
-233
℃
课内练习
课堂练习
4.下列说法正确的是( )
A.有理数是指整数、分数、零、正有理数、负有理数这五类
B.一个有理数不是正数就是负数
C.一个有理数不是整数就是分数
D.以上说法都正确
6.下列说法不正确的是( )
A.0既不是正数,也不是负数
B.0的绝对值是0
C.一个有理数不是整数就是分数
D.1是绝对值最小的正数
11.观察下列数的规律,填上合适的数:1,﹣4,9,﹣16,25,﹣36,49,
.
解:根据题意,第几个数的绝对值就是序数几的平方,且序数是奇数时是正数,序数是偶数时是负数;要填的是第八个,所以应该是﹣82=﹣64;故应填﹣64.
14.将下列各数填在相应的圆圈里:
+6,﹣8,75,﹣0.4,0,23%,,﹣2006,﹣1.8;
﹣
解:故答案为:
15.把几个数用大括号围起来,中间用逗号断开,如:{1,2,﹣3},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数﹣a+10也必是这个集合的元素,这样的集合我们称为和谐的集合.例如集合{10,0}就是一个和谐集合.(1)请你判断集合{﹣1,2},{﹣2,1,5,9,12}是不是和谐集合?
(2)请你再写出两个和谐的集合(至少有一个集合含有三个元素).
(3)写出所有和谐的集合中,元素个数最少的集合.
【分析】(1)根据和谐集合的定义,只要判断两数相加是否等于10即可.
(2)根据和谐集合的定义,即可写出两个和谐的集合(至少有一个集合含有三个元素).
(3)根据和谐集合的定义,确定元素个数最少的集合.
15.
解:(1)若a=﹣1,则﹣a+10=11不在集合{﹣1,2}内,
∴{﹣1,2}不是和谐集合.
∵﹣2+12=10,1+9=10,5+5=10,
∴{﹣2,1,5,9,12}是和谐集合.
(2)根据和谐集合的定义可知a+10﹣a=10,只要集合中两个数之和为10即可,∵1+9=2+8=3+7=4+6,
∴{2,5,8}和{1,9,2,8,3,7}是和谐集合.
(3)∵5+5=10,
∴要使素个数最少,则集合{5},满足条件.
课堂总结
1、正数与负数都来自于实际生活;用正、负数可以表示实际问题中具有相反意义的量,例如…
2、小学里学过的大于零的数都是正数;正数前面添放上“-”号的数是负数;0既不是正数,也不是负数,它表示正、负数的界限.
3、有理数的分类方法不是唯一的,可以按整数和分数分成两大类,也可以按正有理数、零、负有理数分成三大类.
教材练习题1—3题.
课后作业
https://www.21cnjy.com/help/help_extract.php
人教版
七上
1.1.2从自然数到有理数
知识回顾
1.自然数可以用来计数、测量、标号或排序;分数和小数在实际生活中的应用.
2.数的运算在人们分析、判断、解决实际问题过程中的重要作用
.
3.小学学过的数不够用了,数的范围需要扩展.
具有相反意义的量
收入100元
盈余10元
上升2米
零上5℃
增加25%
…
支出80元
亏损20元
下降3米
零下5℃
减少10%
…
为了表示具有相反意义的量,我们把一种意义的量规定为
正,用大于零的数,如123,36,
,1.31等来表示,这样的数
就叫做正数.正数前面可以放上正号“+”来表示(常省略不
写);把另一种与之意义相反的量规定为负,用大于零的数前
面放上负号“-”来表示,如-233,-60,
,-0.5等,这样的
数就叫做负数.
为了表示具有相反意义的量,我们把其中的一种意义的量规定为正,小学学过的数(零除外),如123,25,2.5等数叫做正数(positive
number).正数前面可以放上“+”号(常省略不写).
零既不是正数,也不是负数.
“-”不可以省略!
把另一种与之意义相反的量规定为负,在前面放上负
号“?”来表示,如?233,?60,-0.5等叫做负数
(negative
number).
注意
1.下列四个数中,正整数是( )
A.﹣2
B.﹣1
C.0
D.1
【分析】正整数是指既是正数还是整数,由此即可判定求解.
解:A、﹣2是负整数,故选项错误;
B、﹣1是负整数,故选项错误;
C、0是非正整数,故选项错误;
D、1是正整数,故选项正确.
故选D.
我们把1,2,3,4,…称为正整数;
-1,-2,-3,-4,…称为负整数;
,
,
,4.5,…称为正分数;
,
,
,-4.5,…称为负分数.
有理数的分类
知识小结
正整数、零和负整数统称整数;
整数和分数统称有理数.
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
正分数和负分数统称分数.
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
非负数是
,
非正数是
,
非负整数是
,
非正整数是
.
零和正数
零和正整数
零和负数
零和负整数
(1)零是______________________________;
(2)零不是_____________________________;
正数,
不是负数,
也不是分数
自然数,
是整数,
是有理数
合作探究
解:
22
,
,
0.33是正数;
-8.4
,
,
-9
是负数;
22
,
0,
-9
是整数;
以上所给各数均为有理数.
-8.4
,
,
0.33
,
是分数;
例
下列给出的各数,哪些是正数?哪些是负数?哪些是整数?哪些是分数?哪些是有理数?
-8.4,22,
,0.33,0,
,-9.
例题讲解
3.把下列各数分别填在相应的集合里:
-1,
,0.3,0,-1.7,21,-2,1.01001,+6.
(1)正数集合{
…}
(2)负数集合{
…}
(3)正整数集合{
…}
(4)分数集合{
…}.
解:(1)正数集合{
,0.3,21,1.01001,+6,…}
(2)负数集合{-1,-1.7,-2,…}
(3)正整数集合{21,+6,…}
(4)分数集合{
,0.3,-1.7,1.01001,…}
变式练习
(1)汽车在一条南北走向的高速公路上行驶,规定向北行驶的路程为正.汽车向北行驶75
km,记做______km(或____km),汽车向南行驶100km,记做________km;
(2)如果向银行存入50元记为50元,那么-30.50元表示______________________;
(3)规定增加的百分比为正,增加25%记做_______,-12%表示___________;
1、填空:
75
+75
-100
从银行取出30.50元
25%
减少12%
(4)规定温度零上为正,月球白天气温高达零上123℃
,记为__________,夜晚气温低至零下233
℃,记为________.阿波罗11号宇航员登上月球后不得不穿着御寒又防热的太空服.
+123℃
-233
℃
课内练习
课堂练习
4.下列说法正确的是( )
A.有理数是指整数、分数、零、正有理数、负有理数这五类
B.一个有理数不是正数就是负数
C.一个有理数不是整数就是分数
D.以上说法都正确
6.下列说法不正确的是( )
A.0既不是正数,也不是负数
B.0的绝对值是0
C.一个有理数不是整数就是分数
D.1是绝对值最小的正数
11.观察下列数的规律,填上合适的数:1,﹣4,9,﹣16,25,﹣36,49,
.
解:根据题意,第几个数的绝对值就是序数几的平方,且序数是奇数时是正数,序数是偶数时是负数;要填的是第八个,所以应该是﹣82=﹣64;故应填﹣64.
14.将下列各数填在相应的圆圈里:
+6,﹣8,75,﹣0.4,0,23%,,﹣2006,﹣1.8;
﹣
解:故答案为:
15.把几个数用大括号围起来,中间用逗号断开,如:{1,2,﹣3},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数﹣a+10也必是这个集合的元素,这样的集合我们称为和谐的集合.例如集合{10,0}就是一个和谐集合.(1)请你判断集合{﹣1,2},{﹣2,1,5,9,12}是不是和谐集合?
(2)请你再写出两个和谐的集合(至少有一个集合含有三个元素).
(3)写出所有和谐的集合中,元素个数最少的集合.
【分析】(1)根据和谐集合的定义,只要判断两数相加是否等于10即可.
(2)根据和谐集合的定义,即可写出两个和谐的集合(至少有一个集合含有三个元素).
(3)根据和谐集合的定义,确定元素个数最少的集合.
15.
解:(1)若a=﹣1,则﹣a+10=11不在集合{﹣1,2}内,
∴{﹣1,2}不是和谐集合.
∵﹣2+12=10,1+9=10,5+5=10,
∴{﹣2,1,5,9,12}是和谐集合.
(2)根据和谐集合的定义可知a+10﹣a=10,只要集合中两个数之和为10即可,∵1+9=2+8=3+7=4+6,
∴{2,5,8}和{1,9,2,8,3,7}是和谐集合.
(3)∵5+5=10,
∴要使素个数最少,则集合{5},满足条件.
课堂总结
1、正数与负数都来自于实际生活;用正、负数可以表示实际问题中具有相反意义的量,例如…
2、小学里学过的大于零的数都是正数;正数前面添放上“-”号的数是负数;0既不是正数,也不是负数,它表示正、负数的界限.
3、有理数的分类方法不是唯一的,可以按整数和分数分成两大类,也可以按正有理数、零、负有理数分成三大类.
教材练习题1—3题.
课后作业
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
