浙教版八年级上册数学课件:1.1认识三角形(共21张PPT)
文档属性
| 名称 | 浙教版八年级上册数学课件:1.1认识三角形(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 848.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
2
1.1认识三角形
第一课时
学习目标
1、认识三角形的概念及其基本要素。
2、能证出三角形内角和是180°
3、熟练掌握三角形的内角和是180°及其应用。
2
请大家仔细观察一组图片,看看主要是有那种几何图形构成?
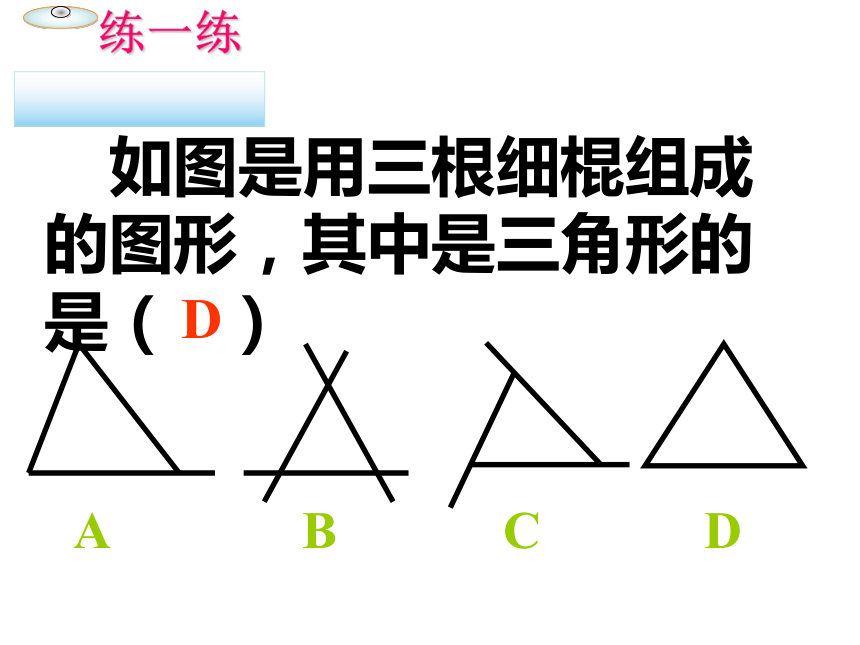
如图是用三根细棍组成的图形,其中是三角形的是(
)
D
三角形的概念:
观察下图三角形是由什么图形怎样构成的?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
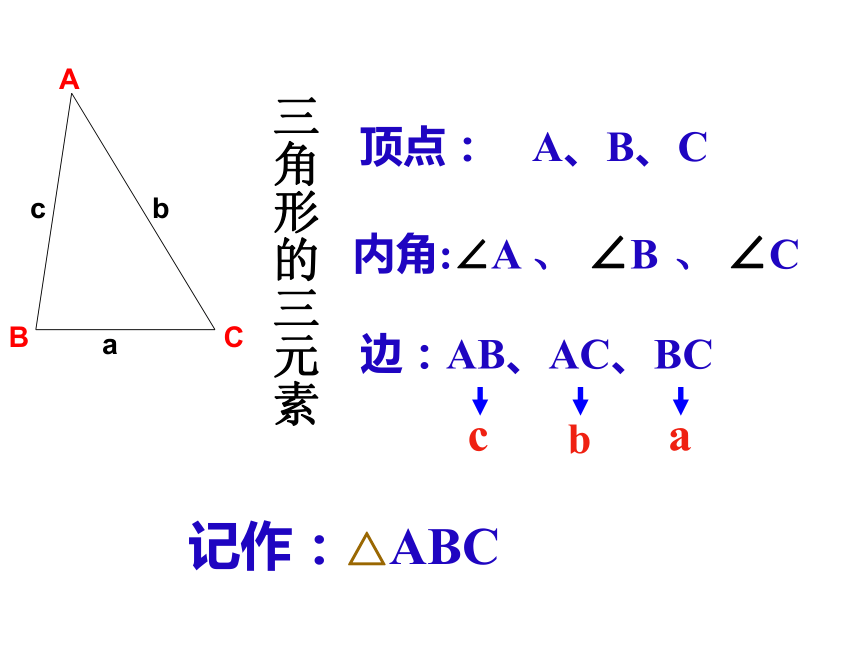
记作:△ABC
顶点:
A、B、C
边:AB、AC、BC
内角:∠A
、
∠B
、
∠C
c
b
a
三角形的三元素
c
b
a
A
B
C
自主学习
三角形的三个内角和是多少?
把三个角拼在一起试试看
有什么办法可以验证呢?
A
B
D
C
如图,撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
拼一拼,说一说
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180?”吗?
结论:三角形的三个内角之和等于180?。
三角形的三个内角和等于180°
结论对任意三角形都成立吗?
如何证明呢?
A
过C作CE∥BA,
)
E
1
。
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(两直线平行,同位角相等)
)
B
C
(等量代换)
证法1:
作BC的延长线CD,
证法2:
A
B
C
过A作ED∥BC,
E
D
∴∠B=∠BAE
(两直线平行,内错角相等)
∠C=∠CAD
(两直线平行,内错角相等)
又∵∠BAE+∠CAD+∠BAC=180°
∴∠B+∠C+∠BAC=180°
(平角的定义)
(等量代换)
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
三角形内角和定理:
三角形的内角和等于1800.
证法3:
C
B
A
过C作CD∥BA,
D
∴∠B=∠BCD
(两直线平行,内错角相等)
∠BCD+∠BCA+∠A=180°
(两直线平行,同旁内角互补)
∴∠B+∠BCA+∠A=180°
(等量代换)
例
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,
C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
检验一下自己吧!
1、
在△ABC中,∠A=80°,∠B=∠C
,
求∠C的度数。
解:在△ABC中,
∠A+∠B+∠C=180°,
∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
2、已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为20°,60°,100°。
达标测试
1△ABC中,若∠A+∠B=∠C,则△ABC是()
A、锐角△ B、直角△ C、钝角△ D、等腰△
2
一个三角形至少有()
A、一个锐角 B、两个锐角 C、一个钝角
D、一个直角
3
如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,
∠B=50°,求∠BDC的度数。
动脑筋,你能行!
如图△ABC中,∠ABC、∠ACB的平分线交于点O,
⑴若∠A=70°,求∠BOC。
⑵若∠A=x°,求∠BOC。
动脑筋,你能行!
能力提高
2
1.1认识三角形
第一课时
学习目标
1、认识三角形的概念及其基本要素。
2、能证出三角形内角和是180°
3、熟练掌握三角形的内角和是180°及其应用。
2
请大家仔细观察一组图片,看看主要是有那种几何图形构成?
如图是用三根细棍组成的图形,其中是三角形的是(
)
D
三角形的概念:
观察下图三角形是由什么图形怎样构成的?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
记作:△ABC
顶点:
A、B、C
边:AB、AC、BC
内角:∠A
、
∠B
、
∠C
c
b
a
三角形的三元素
c
b
a
A
B
C
自主学习
三角形的三个内角和是多少?
把三个角拼在一起试试看
有什么办法可以验证呢?
A
B
D
C
如图,撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
拼一拼,说一说
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180?”吗?
结论:三角形的三个内角之和等于180?。
三角形的三个内角和等于180°
结论对任意三角形都成立吗?
如何证明呢?
A
过C作CE∥BA,
)
E
1
。
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(两直线平行,同位角相等)
)
B
C
(等量代换)
证法1:
作BC的延长线CD,
证法2:
A
B
C
过A作ED∥BC,
E
D
∴∠B=∠BAE
(两直线平行,内错角相等)
∠C=∠CAD
(两直线平行,内错角相等)
又∵∠BAE+∠CAD+∠BAC=180°
∴∠B+∠C+∠BAC=180°
(平角的定义)
(等量代换)
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
三角形内角和定理:
三角形的内角和等于1800.
证法3:
C
B
A
过C作CD∥BA,
D
∴∠B=∠BCD
(两直线平行,内错角相等)
∠BCD+∠BCA+∠A=180°
(两直线平行,同旁内角互补)
∴∠B+∠BCA+∠A=180°
(等量代换)
例
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,
C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度?
检验一下自己吧!
1、
在△ABC中,∠A=80°,∠B=∠C
,
求∠C的度数。
解:在△ABC中,
∠A+∠B+∠C=180°,
∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
2、已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为20°,60°,100°。
达标测试
1△ABC中,若∠A+∠B=∠C,则△ABC是()
A、锐角△ B、直角△ C、钝角△ D、等腰△
2
一个三角形至少有()
A、一个锐角 B、两个锐角 C、一个钝角
D、一个直角
3
如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,
∠B=50°,求∠BDC的度数。
动脑筋,你能行!
如图△ABC中,∠ABC、∠ACB的平分线交于点O,
⑴若∠A=70°,求∠BOC。
⑵若∠A=x°,求∠BOC。
动脑筋,你能行!
能力提高
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
