二次函数系数与图象的关系
图片预览






文档简介
(共22张PPT)
图象与系数的关系
3、感悟数形结合的意义。
1、理解二次函数的图象与a 、b、c符号之间的关系。
2、能根据二次函数的图像正确判断a 、b、c的符号。
字母的符号 图象的特征
a
ab
c
Δ
a>0
a<0
开口向上
b=0
ab>0
ab<0
c=0
c>0
c<0
Δ=0
Δ>0
Δ<0
开口向下
对称轴为y轴
对称轴在y轴的左侧
对称轴在y轴的右侧
抛物线过原点
与y轴正半轴相交
与y轴负半轴相交
与x轴有唯一交点
与x轴有两个交点
与x轴没有交点
字母的符号 图象的特征
a+b+c
a-b+c
a+b+c>0
X=1时抛物线上的点位于x轴的上方
X=1时抛物线上的点位于x轴上
X=1时抛物线上的点位于x轴的下方
X=-1时抛物线上的点位于x轴的上方
X=-1时抛物线上的点位于x轴上
X=-1时抛物线上的点位于x轴的下方
a+b+c=0
a+b+c<0
a-b+c>0
a-b+c=0
a-b+c<0
你还可想到啥?
利用以上知识主要解决以下几方面问题:
(1)由a,b,c, 的符号确定抛物线在坐标系中的大 致位置;
(2)由抛物线的位置确定系数a,b,c, 等符号及有关a,b,c的代数式的符号;
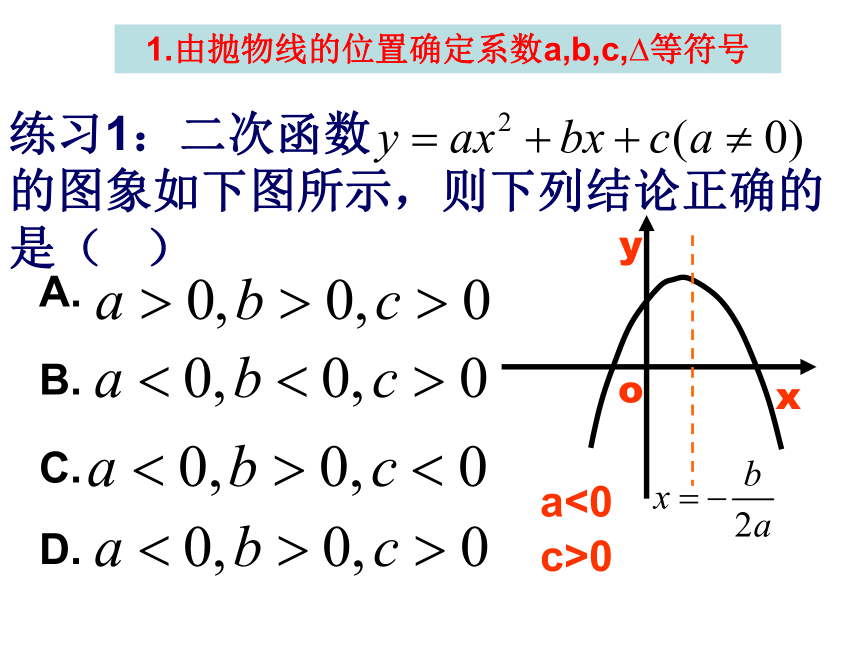
练习1:二次函数 的图象如下图所示,则下列结论正确的是( )
1.由抛物线的位置确定系数a,b,c, 等符号
o
y
x
A.
B.
C.
D.
a<0
c>0
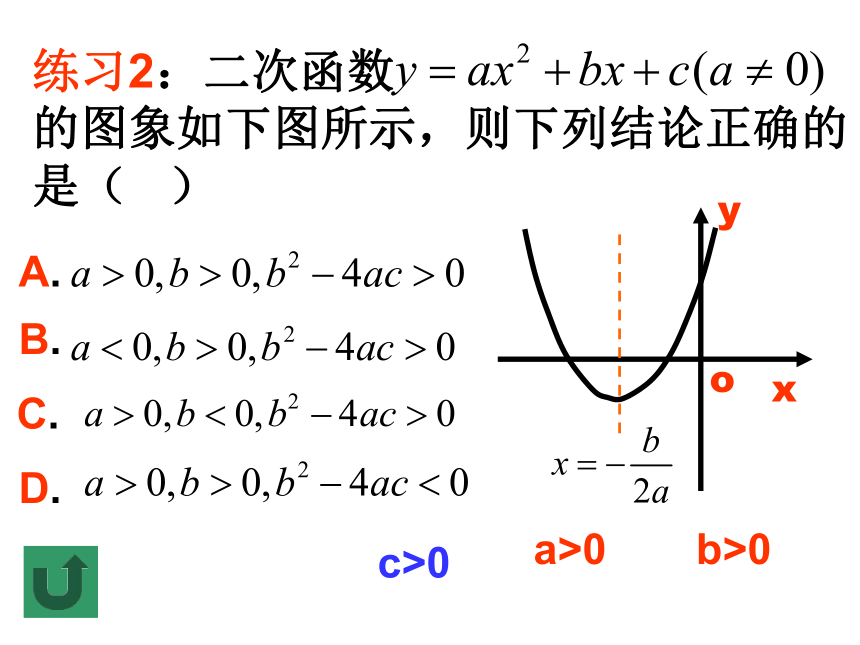
练习2:二次函数 的图象如下图所示,则下列结论正确的是( )
A.
B.
C.
D.
o
y
x
a>0
c>0
b>0
练习3: 抛物线 的图象如下图所示,试确定下列各式的符号:
(1)a ;(2) b; (3)c;
o
y
x
-1
1
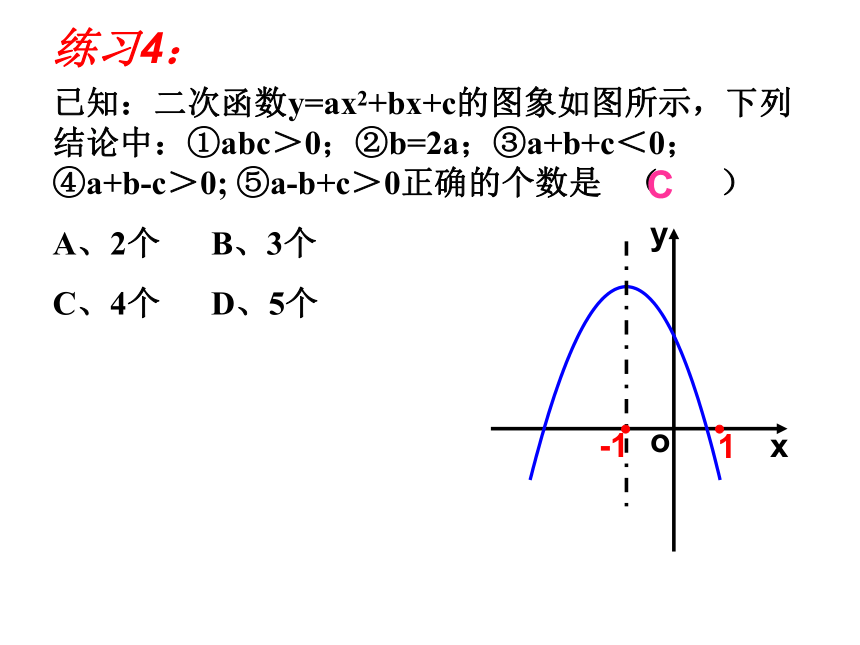
练习4:
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
练习4:如下图,满足b<0,c<0的
的大致图象是( )
2.由解析式确定函数大致图象
o
y
x
o
y
x
o
y
x
o
y
x
A.
B.
C.
D.
驶向胜利的彼岸
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
这节课你有哪些体会?
1.a,b,c等符号与二次函数y=ax2+bx+c有密切的联系;
2.解决这类问题的关键是运用数形结合思想,即会观察图象;如遇到2a+b,2a-b要与对称轴联系等;
3.要注意灵活运用数学知识,具体问题具体分析……
数学因规律而不再枯燥,
数学因思维而耐人寻味。
让我们热爱数学吧!
作业.如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于A点.
(1)根据图象确定a、b、c的符号,并说明理由;
(2)如果点A的坐标
(0,3),∠ABC=45°,∠ACB=60°,
求这个二次函数的解析式.
课堂检测
2.已知:二次函数y=ax2+bx+c的图象如
图所示,判断点M( ,a)在第几象限
x
o
y
3、已知:二次函数y=ax2+bx+c的图象
如图所示,下列结论中:①b>0;
②c<0;③4a+2b+c > 0;④(a+c)2<b2,
判断正误,并说明理由.
x
o
y
x=1
图象与系数的关系
3、感悟数形结合的意义。
1、理解二次函数的图象与a 、b、c符号之间的关系。
2、能根据二次函数的图像正确判断a 、b、c的符号。
字母的符号 图象的特征
a
ab
c
Δ
a>0
a<0
开口向上
b=0
ab>0
ab<0
c=0
c>0
c<0
Δ=0
Δ>0
Δ<0
开口向下
对称轴为y轴
对称轴在y轴的左侧
对称轴在y轴的右侧
抛物线过原点
与y轴正半轴相交
与y轴负半轴相交
与x轴有唯一交点
与x轴有两个交点
与x轴没有交点
字母的符号 图象的特征
a+b+c
a-b+c
a+b+c>0
X=1时抛物线上的点位于x轴的上方
X=1时抛物线上的点位于x轴上
X=1时抛物线上的点位于x轴的下方
X=-1时抛物线上的点位于x轴的上方
X=-1时抛物线上的点位于x轴上
X=-1时抛物线上的点位于x轴的下方
a+b+c=0
a+b+c<0
a-b+c>0
a-b+c=0
a-b+c<0
你还可想到啥?
利用以上知识主要解决以下几方面问题:
(1)由a,b,c, 的符号确定抛物线在坐标系中的大 致位置;
(2)由抛物线的位置确定系数a,b,c, 等符号及有关a,b,c的代数式的符号;
练习1:二次函数 的图象如下图所示,则下列结论正确的是( )
1.由抛物线的位置确定系数a,b,c, 等符号
o
y
x
A.
B.
C.
D.
a<0
c>0
练习2:二次函数 的图象如下图所示,则下列结论正确的是( )
A.
B.
C.
D.
o
y
x
a>0
c>0
b>0
练习3: 抛物线 的图象如下图所示,试确定下列各式的符号:
(1)a ;(2) b; (3)c;
o
y
x
-1
1
练习4:
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
练习4:如下图,满足b<0,c<0的
的大致图象是( )
2.由解析式确定函数大致图象
o
y
x
o
y
x
o
y
x
o
y
x
A.
B.
C.
D.
驶向胜利的彼岸
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
这节课你有哪些体会?
1.a,b,c等符号与二次函数y=ax2+bx+c有密切的联系;
2.解决这类问题的关键是运用数形结合思想,即会观察图象;如遇到2a+b,2a-b要与对称轴联系等;
3.要注意灵活运用数学知识,具体问题具体分析……
数学因规律而不再枯燥,
数学因思维而耐人寻味。
让我们热爱数学吧!
作业.如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于A点.
(1)根据图象确定a、b、c的符号,并说明理由;
(2)如果点A的坐标
(0,3),∠ABC=45°,∠ACB=60°,
求这个二次函数的解析式.
课堂检测
2.已知:二次函数y=ax2+bx+c的图象如
图所示,判断点M( ,a)在第几象限
x
o
y
3、已知:二次函数y=ax2+bx+c的图象
如图所示,下列结论中:①b>0;
②c<0;③4a+2b+c > 0;④(a+c)2<b2,
判断正误,并说明理由.
x
o
y
x=1
