浙教版初中数学八年级上册第1章《三角形的初步认识》测试题(word版含答案)
文档属性
| 名称 | 浙教版初中数学八年级上册第1章《三角形的初步认识》测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 105.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 18:35:45 | ||
图片预览

文档简介
浙教版初中数学八年级上册第1章《三角形的初步认识》测试题
时间:90分钟
满分:100
一、精心选一选,慧眼识金!(每小题3分,共30分)
1、以长为3cm.5cn,7cm,10cm,的四根木棍为边,可以构成三角形的个数是()
A.1个
B.
2个
C.
3个
D.
4个
2、下列说法正确的是(
)
A.三角形的高就是顶点到对边垂线段的长度
B.直角三角形有且仅有一条高
C.
三角形的高都在三角形的内部
D.三角形的三条高至少有一条高在三角形的内部
3、锐角三角形的三个内角是∠A,
∠B,
∠C,如果,,
,那么,,这三个角中()
A.没有锐角
B有1个锐角
C.
有2个锐角
D.
有3个锐角
4、如图1,AB=BD,BC=BE,要使△ABE≌△DBC,需添加条件()
A.
∠A=∠D
B.∠C=∠E
C.
∠D=∠E
D.
∠ABD=∠CBE
5、如图2所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有()
A.2对
B.3对
C.4对
D.
5对
6、要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D使CD=BC,在过点D作出DGF的垂线DE,使A,C,E三点在一条直线上,如图3,可以推出△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是()
A.边角边
B.角边角
C.边边边
D.
斜边、直角边
7、给出下列结论:①三条线段组成的图形叫三角形;②三角形相邻两边组成的角叫三角形的内角;③三角形的角平分线是射线;④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;⑤任何一个三角形都有三条高、三条中线、三条角平分线;⑥三角形的三条角平分线交于一点,且这点在三角形内,正确的结论有()
A.1个
B.
2个
C.
3个
D.
4个
8、如图4,在等腰直角△ABC中,∠B=90°,将△ABC
绕顶点A逆时针方向旋转60°后得到△AB′C′等于()
A.45°
B.
105°
C.
120°
D.
35°
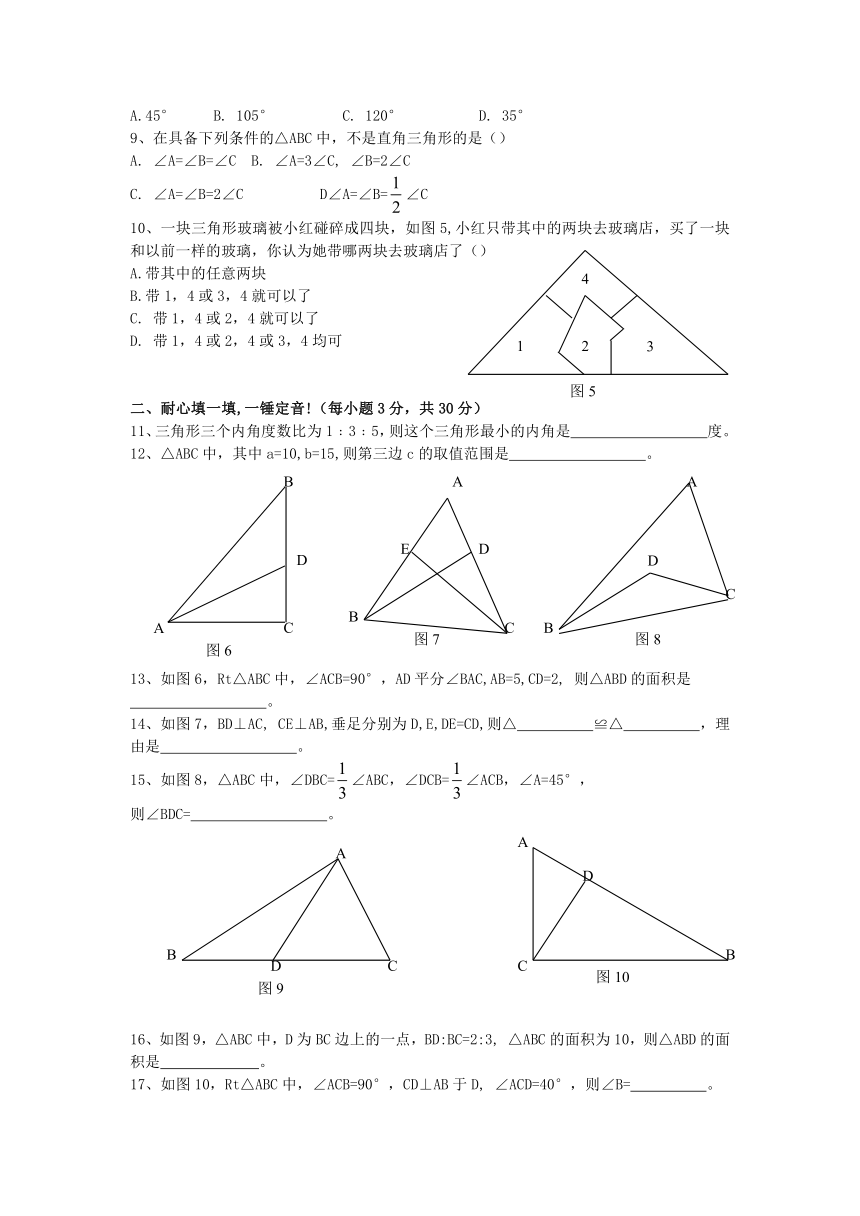
9、在具备下列条件的△ABC中,不是直角三角形的是()
A.
∠A=∠B=∠C
B.
∠A=3∠C,
∠B=2∠C
C.
∠A=∠B=2∠C
D∠A=∠B=∠C
10、一块三角形玻璃被小红碰碎成四块,如图5,小红只带其中的两块去玻璃店,买了一块和以前一样的玻璃,你认为她带哪两块去玻璃店了()
A.带其中的任意两块
B.带1,4或3,4就可以了
C.
带1,4或2,4就可以了
D.
带1,4或2,4或3,4均可
二、耐心填一填,一锤定音!(每小题3分,共30分)
11、三角形三个内角度数比为1﹕3﹕5,则这个三角形最小的内角是
度。
12、△ABC中,其中a=10,b=15,则第三边c的取值范围是
。
13、如图6,Rt△ABC中,∠ACB=90°,AD平分∠BAC,AB=5,CD=2,
则△ABD的面积是
。
14、如图7,BD⊥AC,
CE⊥AB,垂足分别为D,E,DE=CD,则△
≌△
,理由是
。
15、如图8,△ABC中,∠DBC=∠ABC,∠DCB=∠ACB,∠A=45°,
则∠BDC=
。
16、如图9,△ABC中,D为BC边上的一点,BD:BC=2:3,
△ABC的面积为10,则△ABD的面积是
。
17、如图10,Rt△ABC中,∠ACB=90°,CD⊥AB于D,
∠ACD=40°,则∠B=
。
18、如图11,在BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大,若∠A减少度,∠B增加度,∠C增加度,则三者之间的关系是
。
19、如图12,∠1+∠2+∠3+∠4=
度。
20、如图13,△ABC中,AD为中线,
DE⊥AB于E,
DF⊥AC于F,AB=3,AC=4,DF=1.5,则DE=
。
三、专心解一解,马到成功!(每题8分,共40分)
21、如图14,AD⊥BD,AE平分∠BAC,
∠B=30°,∠ACD=70°,求∠DAE的度数。
22、如图16,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE,试说明:
⑴△ABC≌△DEF;
⑵GF=GC.
23、如图17,△ABC中,∠B:∠C=3:4,FD⊥BC,DE⊥AB,且∠AFD=146°,求∠EDF的度数。
24、如图18,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案。
25、如图19,Rt△ABC中,AB=AC,
∠BAC=90°,直线L为经过点A的任一直线,BD⊥L于D,CE⊥L于E,若BD>CE,试问:⑴AD与CE的大小关系如何?请说明理由;
⑵线段BD,DE,CE之间的数量之间关系如何?并说明理由。
参考答案
一、1、B;;2、D;;3、A;4、D;5、B;6、B;7、C;8、A;9、C;10、D。
二、11、20;
12、5<c<25;;
13、5;
14、BEC,CDB,HL;
15、135°;
16、4;
17、40°;
18、;
19、280;
20、2
三、21、∠DAE=40°;
22、⑴因为BF=CE,所以BF+FC=CE+FC,即BC=EF,
又因为AB⊥BE,DE⊥BE,所以∠B=∠E=90°,又因为AB=DE,所以△ABC≌△DEF;
⑵因为△ABC≌△DEF,所以∠ACB=∠DFE,所以GF=GC。
23、因为∠AFD=146°,所以∠DFC=34°,
因为FD⊥BC,所以∠FDC=90°,所以∠C=56°,因为∠B:∠C=3:4,所以∠B=42°,
因为,DE⊥AB,所以∠BED=90°,所以∠EDB=48°,
因为∠EDB+∠EDF=90°,所以∠EDF=42°。
24、设计方案如下:
25、⑴AD=CE,理由:因为BD⊥L于D,CE⊥L于E,所以∠BDA=∠AEC=90°(垂直的定义),
又∠BAD+∠ABD=90°,∠BAD+∠CAE=90°,所以∠ABD=∠CAE(同角的余角相等),
因为AB=CA,所以△ABD≌△CAE(AAS),所以AD=CE(全等三角形的对应边相等)
⑵BD=CE+DE.因为△ABD≌△CAE(已证),所以BD=AE(全等三角形的对应边相等),又因为AE=DE+AD,而AD=CE,所以BD=CE+DE.
A
B
C
D
E
F
图2
A
D
B
E
C
图1
A
B
C
D
E
F
图3
A
B
C
B′
C′
图4
1
2
3
4
图5
A
B
C
E
D
图7
A
B
C
D
图8
A
B
C
D
图6
A
C
B
D
图10
A
B
C
D
图9
A
B
C
图11
图12
A
B
C
D
E
40°
1
2
3
4
A
E
B
D
C
F
图13
A
D
C
E
B
图14
A
B
G
F
C
D
E
图16
A
B
C
D
E
F
图17
图18
A
B
C
D
E
图19
时间:90分钟
满分:100
一、精心选一选,慧眼识金!(每小题3分,共30分)
1、以长为3cm.5cn,7cm,10cm,的四根木棍为边,可以构成三角形的个数是()
A.1个
B.
2个
C.
3个
D.
4个
2、下列说法正确的是(
)
A.三角形的高就是顶点到对边垂线段的长度
B.直角三角形有且仅有一条高
C.
三角形的高都在三角形的内部
D.三角形的三条高至少有一条高在三角形的内部
3、锐角三角形的三个内角是∠A,
∠B,
∠C,如果,,
,那么,,这三个角中()
A.没有锐角
B有1个锐角
C.
有2个锐角
D.
有3个锐角
4、如图1,AB=BD,BC=BE,要使△ABE≌△DBC,需添加条件()
A.
∠A=∠D
B.∠C=∠E
C.
∠D=∠E
D.
∠ABD=∠CBE
5、如图2所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有()
A.2对
B.3对
C.4对
D.
5对
6、要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D使CD=BC,在过点D作出DGF的垂线DE,使A,C,E三点在一条直线上,如图3,可以推出△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是()
A.边角边
B.角边角
C.边边边
D.
斜边、直角边
7、给出下列结论:①三条线段组成的图形叫三角形;②三角形相邻两边组成的角叫三角形的内角;③三角形的角平分线是射线;④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;⑤任何一个三角形都有三条高、三条中线、三条角平分线;⑥三角形的三条角平分线交于一点,且这点在三角形内,正确的结论有()
A.1个
B.
2个
C.
3个
D.
4个
8、如图4,在等腰直角△ABC中,∠B=90°,将△ABC
绕顶点A逆时针方向旋转60°后得到△AB′C′等于()
A.45°
B.
105°
C.
120°
D.
35°
9、在具备下列条件的△ABC中,不是直角三角形的是()
A.
∠A=∠B=∠C
B.
∠A=3∠C,
∠B=2∠C
C.
∠A=∠B=2∠C
D∠A=∠B=∠C
10、一块三角形玻璃被小红碰碎成四块,如图5,小红只带其中的两块去玻璃店,买了一块和以前一样的玻璃,你认为她带哪两块去玻璃店了()
A.带其中的任意两块
B.带1,4或3,4就可以了
C.
带1,4或2,4就可以了
D.
带1,4或2,4或3,4均可
二、耐心填一填,一锤定音!(每小题3分,共30分)
11、三角形三个内角度数比为1﹕3﹕5,则这个三角形最小的内角是
度。
12、△ABC中,其中a=10,b=15,则第三边c的取值范围是
。
13、如图6,Rt△ABC中,∠ACB=90°,AD平分∠BAC,AB=5,CD=2,
则△ABD的面积是
。
14、如图7,BD⊥AC,
CE⊥AB,垂足分别为D,E,DE=CD,则△
≌△
,理由是
。
15、如图8,△ABC中,∠DBC=∠ABC,∠DCB=∠ACB,∠A=45°,
则∠BDC=
。
16、如图9,△ABC中,D为BC边上的一点,BD:BC=2:3,
△ABC的面积为10,则△ABD的面积是
。
17、如图10,Rt△ABC中,∠ACB=90°,CD⊥AB于D,
∠ACD=40°,则∠B=
。
18、如图11,在BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大,若∠A减少度,∠B增加度,∠C增加度,则三者之间的关系是
。
19、如图12,∠1+∠2+∠3+∠4=
度。
20、如图13,△ABC中,AD为中线,
DE⊥AB于E,
DF⊥AC于F,AB=3,AC=4,DF=1.5,则DE=
。
三、专心解一解,马到成功!(每题8分,共40分)
21、如图14,AD⊥BD,AE平分∠BAC,
∠B=30°,∠ACD=70°,求∠DAE的度数。
22、如图16,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE,试说明:
⑴△ABC≌△DEF;
⑵GF=GC.
23、如图17,△ABC中,∠B:∠C=3:4,FD⊥BC,DE⊥AB,且∠AFD=146°,求∠EDF的度数。
24、如图18,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案。
25、如图19,Rt△ABC中,AB=AC,
∠BAC=90°,直线L为经过点A的任一直线,BD⊥L于D,CE⊥L于E,若BD>CE,试问:⑴AD与CE的大小关系如何?请说明理由;
⑵线段BD,DE,CE之间的数量之间关系如何?并说明理由。
参考答案
一、1、B;;2、D;;3、A;4、D;5、B;6、B;7、C;8、A;9、C;10、D。
二、11、20;
12、5<c<25;;
13、5;
14、BEC,CDB,HL;
15、135°;
16、4;
17、40°;
18、;
19、280;
20、2
三、21、∠DAE=40°;
22、⑴因为BF=CE,所以BF+FC=CE+FC,即BC=EF,
又因为AB⊥BE,DE⊥BE,所以∠B=∠E=90°,又因为AB=DE,所以△ABC≌△DEF;
⑵因为△ABC≌△DEF,所以∠ACB=∠DFE,所以GF=GC。
23、因为∠AFD=146°,所以∠DFC=34°,
因为FD⊥BC,所以∠FDC=90°,所以∠C=56°,因为∠B:∠C=3:4,所以∠B=42°,
因为,DE⊥AB,所以∠BED=90°,所以∠EDB=48°,
因为∠EDB+∠EDF=90°,所以∠EDF=42°。
24、设计方案如下:
25、⑴AD=CE,理由:因为BD⊥L于D,CE⊥L于E,所以∠BDA=∠AEC=90°(垂直的定义),
又∠BAD+∠ABD=90°,∠BAD+∠CAE=90°,所以∠ABD=∠CAE(同角的余角相等),
因为AB=CA,所以△ABD≌△CAE(AAS),所以AD=CE(全等三角形的对应边相等)
⑵BD=CE+DE.因为△ABD≌△CAE(已证),所以BD=AE(全等三角形的对应边相等),又因为AE=DE+AD,而AD=CE,所以BD=CE+DE.
A
B
C
D
E
F
图2
A
D
B
E
C
图1
A
B
C
D
E
F
图3
A
B
C
B′
C′
图4
1
2
3
4
图5
A
B
C
E
D
图7
A
B
C
D
图8
A
B
C
D
图6
A
C
B
D
图10
A
B
C
D
图9
A
B
C
图11
图12
A
B
C
D
E
40°
1
2
3
4
A
E
B
D
C
F
图13
A
D
C
E
B
图14
A
B
G
F
C
D
E
图16
A
B
C
D
E
F
图17
图18
A
B
C
D
E
图19
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
