1.3 绝对值 教学课件(共21张PPT)
文档属性
| 名称 | 1.3 绝对值 教学课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 18:40:54 | ||
图片预览







文档简介
绝对值
新知导入
城市里出租车一般按实际载客行驶的里程收费,与行驶的路线、方向无关.
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶6 km到达A处,记______km,乙车向西行驶6 km到达B处,记做_______km.
以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
+6
-6
A、B两点与原点距离分别是6 km,它们的实际意义是甲、乙两辆出租车距出发地6 km.
(2)数轴上表示-4和4的点到原点的距离分别是多少?表示 的和 点呢?
数轴上表示-4和4的点到原点的距离分别是4,表示 的 和 点到原点的距离分别是 .
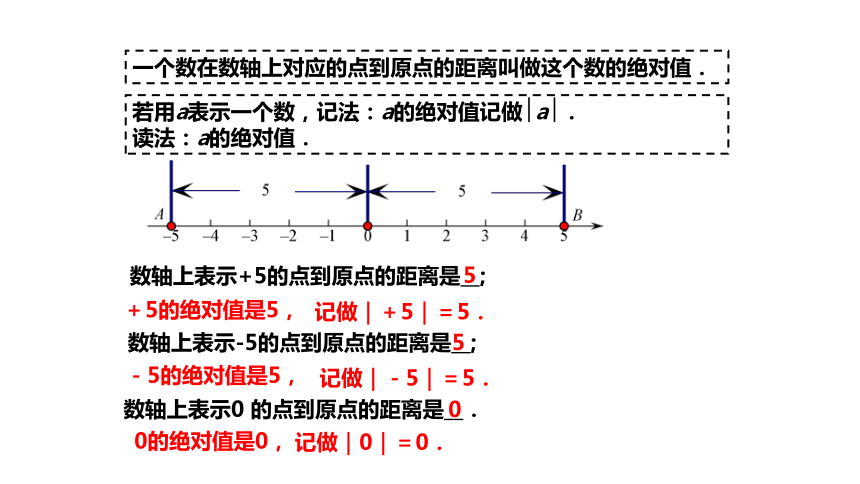
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
数轴上表示+5的点到原点的距离是__;
数轴上表示-5的点到原点的距离是__;
数轴上表示0 的点到原点的距离是__.
+5的绝对值是5,
记做|+5|=5.
-5的绝对值是5,
记做|-5|=5.
0的绝对值是0,
记做|0|=0.
5
5
0
若用a表示一个数,记法:a的绝对值记做?a?.
读法:a的绝对值.
例1 求下列各数的绝对值:
解:在数轴上表示各数如图所示:
∵表示-1.6的点到原点的距离是1.6,∴
∵表示 的点到原点的距离是 ,∴
∵表示0的点到原点的距离是0,∴
∵表示-10的点到原点的距离是10,∴
∵表示10的点到原点的距离是10,∴
例题讲解
例题讲解
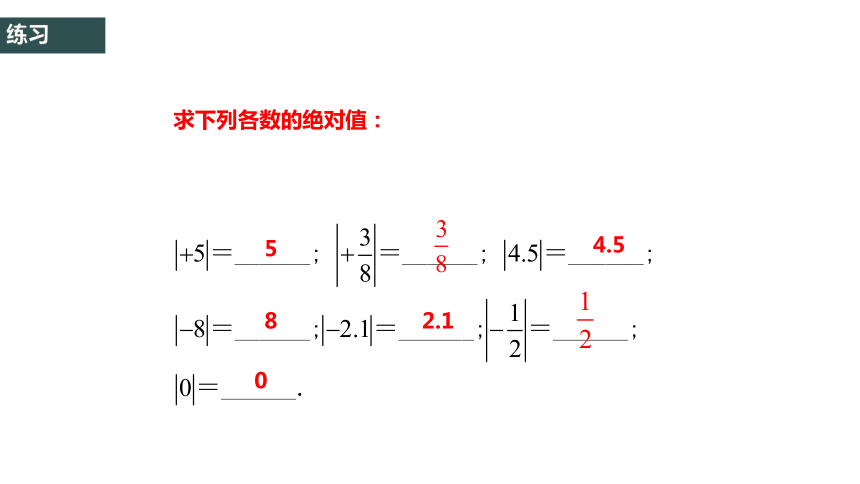
5
4.5
8
2.1
0
求下列各数的绝对值:
练习
1.正数的绝对值是它本身;
如果a>0,那么|a|=a;
2.负数的绝对值是它的相反数;
如果a<0,那么|a|=-a;
3.0的绝对值是0;
如果a=0,那么|a|=0;
4.互为相反数的两个数的绝对值相等.
如果a与b互为相反数,那么|a|=|b|.
总结
| a | =
( a > 0 )
a
( a = 0 )
0
( a < 0 )
-a
任一有理数的绝对值是一个非负数.
有绝对值小于本身的数吗?一个数的绝对值是什么数?由此你能得到绝对值的什么性质?
例2 求绝对值等于4的数.
解:因为数轴上到原点的距离等于4个单位长度的点有两个(如图),即表示+4的点和表示-4的点,所以绝对值等于4的数是+4和-4.
例题讲解
绝对值等于0的数是___,
绝对值等于3.14的正数是 ,
绝对值等于2的负数是______,
绝对值等于1的数是_______.
0
3.14
-2
1或-1
练习
课堂练习
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.如果一个数是负数,那么这个数的绝对值是它的相反数
D.绝对值越大,这个数就越大
2.已知|a+1|与|b﹣4|互为相反数,则ab的值是( )
A.﹣1 B.1 C.﹣4 D.4
3.设x是有理数,那么下列各式中一定表示正数的是( )
A.2015x B.x+2015 C.|2015x| D.|x|+2015
4.若|x﹣1|+|y+2|+|z﹣3|=0.则x+y+z的值为( )
A.2 B.﹣2 C.0 D.6
5.同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)求|4﹣(﹣2)|= ;
(2)若|x﹣2|=5,则x= ;
(3)请你找出所有符合条件的整数x,使得|1﹣x|+|x+2|=3.
解:(1)原式=6;
5.同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)求|4﹣(﹣2)|= ;
(2)若|x﹣2|=5,则x= ;
(3)请你找出所有符合条件的整数x,使得|1﹣x|+|x+2|=3.
(2)∵|x﹣2|=5,
∴x﹣2=±5,
∴x=7或﹣3;
5.同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)求|4﹣(﹣2)|= ;
(2)若|x﹣2|=5,则x= ;
(3)请你找出所有符合条件的整数x,使得|1﹣x|+|x+2|=3.
(3)由题意可知:|1﹣x|+|x+2|表示数x到1和﹣2的距离之和,
∴﹣2≤x≤1,
∴x=﹣2或﹣1或0或1.
故答案为(1)6;(2)7或﹣3;
课堂总结
1.绝对值的意义.
代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;零的绝对值是零.
几何意义:数轴上表示这个数的点到原点的距离.
2.绝对值的非负性:|a|≥0
3.绝对值与相反数的关系:
互为相反数的两个数的绝对值相等.
4.绝对值等于本身的数是:0和正数(即非负数)
5.绝对值为正数,则原数有2个,且互为相反数.
课后作业
教材练习题
谢
谢
观
看
新知导入
城市里出租车一般按实际载客行驶的里程收费,与行驶的路线、方向无关.
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶6 km到达A处,记______km,乙车向西行驶6 km到达B处,记做_______km.
以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
+6
-6
A、B两点与原点距离分别是6 km,它们的实际意义是甲、乙两辆出租车距出发地6 km.
(2)数轴上表示-4和4的点到原点的距离分别是多少?表示 的和 点呢?
数轴上表示-4和4的点到原点的距离分别是4,表示 的 和 点到原点的距离分别是 .
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
数轴上表示+5的点到原点的距离是__;
数轴上表示-5的点到原点的距离是__;
数轴上表示0 的点到原点的距离是__.
+5的绝对值是5,
记做|+5|=5.
-5的绝对值是5,
记做|-5|=5.
0的绝对值是0,
记做|0|=0.
5
5
0
若用a表示一个数,记法:a的绝对值记做?a?.
读法:a的绝对值.
例1 求下列各数的绝对值:
解:在数轴上表示各数如图所示:
∵表示-1.6的点到原点的距离是1.6,∴
∵表示 的点到原点的距离是 ,∴
∵表示0的点到原点的距离是0,∴
∵表示-10的点到原点的距离是10,∴
∵表示10的点到原点的距离是10,∴
例题讲解
例题讲解
5
4.5
8
2.1
0
求下列各数的绝对值:
练习
1.正数的绝对值是它本身;
如果a>0,那么|a|=a;
2.负数的绝对值是它的相反数;
如果a<0,那么|a|=-a;
3.0的绝对值是0;
如果a=0,那么|a|=0;
4.互为相反数的两个数的绝对值相等.
如果a与b互为相反数,那么|a|=|b|.
总结
| a | =
( a > 0 )
a
( a = 0 )
0
( a < 0 )
-a
任一有理数的绝对值是一个非负数.
有绝对值小于本身的数吗?一个数的绝对值是什么数?由此你能得到绝对值的什么性质?
例2 求绝对值等于4的数.
解:因为数轴上到原点的距离等于4个单位长度的点有两个(如图),即表示+4的点和表示-4的点,所以绝对值等于4的数是+4和-4.
例题讲解
绝对值等于0的数是___,
绝对值等于3.14的正数是 ,
绝对值等于2的负数是______,
绝对值等于1的数是_______.
0
3.14
-2
1或-1
练习
课堂练习
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.如果一个数是负数,那么这个数的绝对值是它的相反数
D.绝对值越大,这个数就越大
2.已知|a+1|与|b﹣4|互为相反数,则ab的值是( )
A.﹣1 B.1 C.﹣4 D.4
3.设x是有理数,那么下列各式中一定表示正数的是( )
A.2015x B.x+2015 C.|2015x| D.|x|+2015
4.若|x﹣1|+|y+2|+|z﹣3|=0.则x+y+z的值为( )
A.2 B.﹣2 C.0 D.6
5.同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)求|4﹣(﹣2)|= ;
(2)若|x﹣2|=5,则x= ;
(3)请你找出所有符合条件的整数x,使得|1﹣x|+|x+2|=3.
解:(1)原式=6;
5.同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)求|4﹣(﹣2)|= ;
(2)若|x﹣2|=5,则x= ;
(3)请你找出所有符合条件的整数x,使得|1﹣x|+|x+2|=3.
(2)∵|x﹣2|=5,
∴x﹣2=±5,
∴x=7或﹣3;
5.同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)求|4﹣(﹣2)|= ;
(2)若|x﹣2|=5,则x= ;
(3)请你找出所有符合条件的整数x,使得|1﹣x|+|x+2|=3.
(3)由题意可知:|1﹣x|+|x+2|表示数x到1和﹣2的距离之和,
∴﹣2≤x≤1,
∴x=﹣2或﹣1或0或1.
故答案为(1)6;(2)7或﹣3;
课堂总结
1.绝对值的意义.
代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;零的绝对值是零.
几何意义:数轴上表示这个数的点到原点的距离.
2.绝对值的非负性:|a|≥0
3.绝对值与相反数的关系:
互为相反数的两个数的绝对值相等.
4.绝对值等于本身的数是:0和正数(即非负数)
5.绝对值为正数,则原数有2个,且互为相反数.
课后作业
教材练习题
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
