第4章 代数式单元测试卷（含解析）

中小学教育资源及组卷应用平台
七年级数学上册
代数式
单元测试卷
（满分100分）
题号
一
二
三
四
总分
得分
一、选择题（本大题共10小题，共30.0分）
m与的积，应写成????
A.
B.
C.
D.
一个两位数，十位数字是a，个位数字是b，则这个两位数为（
）．
A.
ab
B.
10a
+b
C.
10b
+a
D.
a
+b
如图，用代数式表示图中阴影部分的面积为（
）
A.
B.
C.
D.
下列计算中：①；②；③；④；⑤若.错误的个数有（
）
A.
1个
B.
2个
C.
3个
D.
4个
下列说法正确的是（
）
A.
单项式的系数是-3
B.
单项式的次数是7
C.
多项式是四次三项式
D.
多项式的项分别是
若单项式2xmy3与单项式-5xyn是同类项，则m和n的值为（?
?）.
A.
m=0，n=3
B.
m=-5，n=2
C.
m=0，n=2
D.
m=1，n=3
今年某药品的单价比去年上涨了10％，若今年的单价是a元，则去年的单价为（
）
A.
(1＋10％)a元
B.
(1－10％)a元
C.
元
D.
元
已知多项式mx+nx合并同类项后，结果为零，则下列说法正确的是（
）
A.
m=n=0
B.
m=n
C.
m-n=0
D.
m+n=0
若时，的值为10，则当时，的值为（?????
）
A.
-10
B.
0
C.
6
D.
10
如果从一卷粗细均匀的电线上截取1m长的电线，称得它的质量为ag，再称得剩余电线的质量为bg，那么原来这卷电线的总长度是（
）
A.
B.
C.
D.
二、填空题（本大题共10小题，共30.0分）
若a，b互为相反数，c，d互为倒数，则(a＋b﹣1)(cd＋1)的值为_________．
若a2＋5ab－b2＝0(ab≠0)，则－的值为??????????．
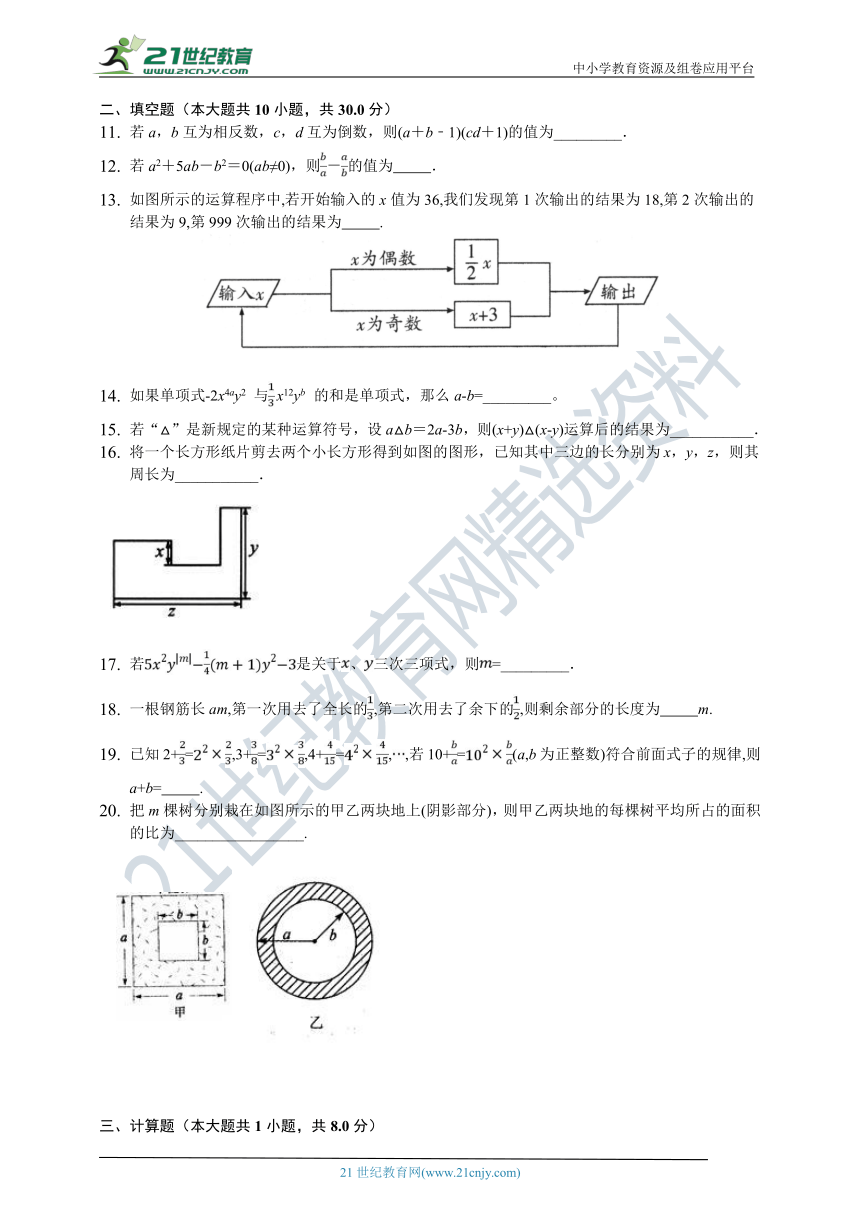
如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,第999次输出的结果为??????????.
如果单项式-2x4ay2?
与?x12yb
?的和是单项式，那么a-b=_________。
若“△”是新规定的某种运算符号，设a△b＝2a-3b，则(x+y)△(x-y)运算后的结果为___________．
将一个长方形纸片剪去两个小长方形得到如图的图形，已知其中三边的长分别为x，y，z，则其周长为___________．
若是关于、三次三项式，则=_________．
一根钢筋长am,第一次用去了全长的,第二次用去了余下的,则剩余部分的长度为??????????m.
已知2+=,3+=,4+=,,若10+=(a,b为正整数)符合前面式子的规律,则a+b=??????????.
把m棵树分别栽在如图所示的甲乙两块地上(阴影部分)，则甲乙两块地的每棵树平均所占的面积的比为_________________.
三、计算题（本大题共1小题，共8.0分）
先化简，再求值．
（1）（
3x2+y2-5xy）+（-4xy-y2+7x2），其中x=2，．
（2）-8m2+[7m2-2m-（3m2-4m）]，其中．
四、解答题（本大题共5小题，共32.0分）
树的高度与树生长的年数有关，测得某棵树的有关数据如下表：（树苗原高100厘米）
年数a
高度h（单位：厘米）
1
115
2
130
3
145
4
…
……
（1）在上表中，填出第4年树苗可能达到的高度；
（2）请用含a的代数式表示高度h＝____________。
（3）用你得到的代数式求生长了10年后的树苗可能达到的高度。
某校团委组织了有奖征文活动，并设立了一、二、三等奖，根据设奖情况买了50件奖品，其二等奖奖品的件数比一等奖奖品的件数的2倍少10，各种奖品的单价如下表所示：
一等奖奖品
二等奖奖品
三等奖奖品
单价/元
13
8
5
数量/件
如果计划一等奖奖品买件，买50件奖品的总花费是y元.
（1）先填表，再用含的代数式表示y并化简；
（2）若一等奖奖品买10件，则共花费多少？
如图，有长为m米的铁栏杆，利用它和一面墙围成一个长方形的花圃，其中长方形的宽为n米．
（1）用含m、n的代数式表示花圃的面积；
（2）当m=24，n=6时，求花圃的面积．
一种蔬菜有x(kg)，不加工直接出售，每千克可卖y元；如果经过加工质量减少了20%，价格增加了40%.问：
(1)x(kg)这种蔬菜加工后可卖多少钱？
(2)如果有这种蔬菜1000
kg，不加工直接出售，每千克可卖1.50元.1000
kg这种蔬菜加工后可卖多少钱？比加工前多卖多少钱？
已知多项式A.
B,其中,某同学在计算A+B时,由于粗心把A+B看成了A?B求得结果为，请你算出A+B的正确结果。
答案和解析
1.【答案】C
【解析】本题考查了列代数式，代数式的书写规则，根据书写规则对各项进行判定即可.本题较为简单，对各选项进行分析，看是否符合代数式正确的书写要求，即可求出答案.
2.【答案】B
【解析】此题考查了列代数式，以及两位数的表示方法，数字的表示方法要牢记．两位数字的表示方法：十位数字×10+个位数字.用十位上的数字乘以10，加上个位上的数字，即可列出这个两位数．
3.【答案】B
【解析】本题考查的知识点是列代数式，把原图形还原成一个矩形，再把阴影部分面积分割在两个矩形中，由此得出阴影部分面积恰好是长为a，宽为5的矩形面积的一半，由此表示阴影部分面积即可．
，
4.【答案】D
【解析】本题主要考查合并同类，熟练掌握合并同类法则是解题的关键，分别利用合并同类项法则判断得出即可．
5.【答案】C
【解析】本题考查了单项式及多项式的定义，解题的关键是牢记单项式的系数、次数及多项式的次数、项数，难度不大.利用多项式及单项式的有关定义分别判断后即可确定正确的选项.
6.【答案】D
【解析】本题考查同类项，根据同类项的概念：含有相同的字母，相同字母的指数相同进行判断.
7.【答案】C
【解析】本题考查列代数式，属于基础题．可根据题意设去年单价为x元，然后根据题意列出等式即可．
8.【答案】D
9.【答案】A
10.【答案】B
【解析】本题主要考查了列代数式的知识点，解决问题的关键是读懂题意，找到所求量的等量关系列出代数式；首先根据1m长的电线，称得它的质量为ag，则剩余电线的质量为bg，其长度是m，所以这卷电线的总长度是（+1）m．
11.【答案】-2
【解析】本题考查了相反数，倒数的定义，代数式求值，根据相反数和倒数的定义得到a+b=0，cd=1，整体代入到代数式中解答即可.
12.【答案】5
13.【答案】3
【解析】本题主要考查的是求代数式的值，找出其中的规律是解题的关键．?
第3次，把x=9代入运算程序中,得9+3=12;
第4次，把x=12代入运算程序中,得12=6;
第5次，把x=6代入运算程序中,得6=3;
第6次，把x=3代入运算程序中,得3+3=6;
依此类推，第999次输出的结果为3.
14.【答案】1
【解析】本题考查了同类项的定义，同类项定义中的两个“相同”：相同字母的指数相同，是易混点，因此成了中考的常考点．根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程，求出a，b的值，再代入代数式计算即可．
15.【答案】?-x+5y
【解析】本题考查的是整式的加减，熟知整式的加减，去括号、合并同类项是解答此题的关键．根据题意得出关于x与y的式子，再去括号，合并同类项即可．
16.【答案】2x+2y+2z
【解析】本题考查了列代数式，正确找出各边之间的关系是解题的关键.根据题意及图示，找出各边之间的对应关系，列出多边形周长的代数式即可.
17.【答案】1
【解析】此题主要考查了多项式的定义，得出关于m的等式和不等式是解题关键．直接利用多项式的概念得出，m+1≠0求出m的值即可．
18.【答案】a
【解析】本题考查了列代数式，解决问题的关键是读懂题意，找到所求量的等量关系．
先求第一次剩下了（1-）a米，再求第二次用去了余下的后剩下：（1-）a×=a．
19.【答案】109
【解析】本题主要考查数字规律问题，解题的关键是根据题意得出规律.根据已知可得等式，据此得出a、b的值，继而可得答案.
20.【答案】?1：π.
【解析】本题考查列代数式有关知识，甲块地阴影部分的面积等于大正方形的面积减去小正方形的面积；乙块地阴影部分的面积等于大圆的面积减去小圆的面积；先求出它们的面积，进一步即可求解．
=1：π．
21.【答案】（1）原式=3x2+y2-5xy-4xy-y2+7x2=10x2-9xy，
当x=2，y=时，原式=40-27=13；
（2）原式=-8m2+7m2-2m-3m2+4m=-4m2+2m，
当m=-时，原式=-1-1=-2．
【解析】此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
22.【答案】???
（1）160；
（2）15a+100；
（3）当a=10时，h=15×10+100=250（厘米）.
答：生长了10年后的树苗可能达到的高度是250厘米.
【解析】本题考查了代数式求值，正确理解高度每年增加15厘米这一规律是关键．
23.【答案】（1）二等奖是：2x-10（件），
三等奖是：50-x-（2x-10）=50-x-2x+10=60-3x（件），
用含有x的代数式表示y是：
y=12x+（2x-10）×10+（60-3x）×5
=
12x+20x-200+300-15x
=
17x+100；
（2）当x=10时，y=17×10+200=370（元），
答：若一等奖奖品买10件，共花费370元.
【解析】此题主要是考查统计表的填写、用含有字母的式子表示数及单价、数量、总价之间的关系等
24.【答案】（1）花圃的面积为：n（m-2n）．
（2）当m=24，n=6时，
原式=6×（24-2×6）=72（米2）．
答：花圃的面积为72米2．
【解析】本题考查的是列代数式和求代数式的值，正确表示出矩形的长是解题的关键．
25.【答案】
（1）x千克这种蔬菜加工后的重量为x（1-20%）千克，价格为y（1+40%）元，
x千克这种蔬菜加工后可卖：x（1-20%）·y（1+40%）＝1.12xy（元）；
（2）当x=1000，y=1.50时，
1.12xy=1.12×1000×1.50＝1680（元），
∴加工后可卖1680元；
又∵1.12xy-xy＝0.12xy，
当x=1000，y=1.50时，
0.12xy＝0.12×1000×1.50＝180（元），
∴比加工前多卖180元.
答：1000kg这种蔬菜加工后可卖1680元，比加工前多卖180元.
【解析】本题考查了列代数式，代数式求值，解题的关键是读懂题意，找到所求的量的等量关系，还要掌握销售问题的价格和重量之间的关系.
26.【答案】
解：∵A=x2+2x-1，A-B=-3x2+2x-1，
∴B
=A
-（A-B）
A+B=2A-（A-B）=2x2+4x-2-（-3x2+2x-1）=2x2+4x-2+3x2-2x+1=5x2+2x-1．
【解析】此题考查了整式的加减，熟练掌握运算法则是解本题的关键．
根据题意列出关系式，去括号合并即可得到结果．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)