浙教版八年级下册 第4章 平行四边形 培优讲义(含解析)
文档属性
| 名称 | 浙教版八年级下册 第4章 平行四边形 培优讲义(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 423.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-14 00:00:00 | ||
图片预览




文档简介
平行四边形
第1讲
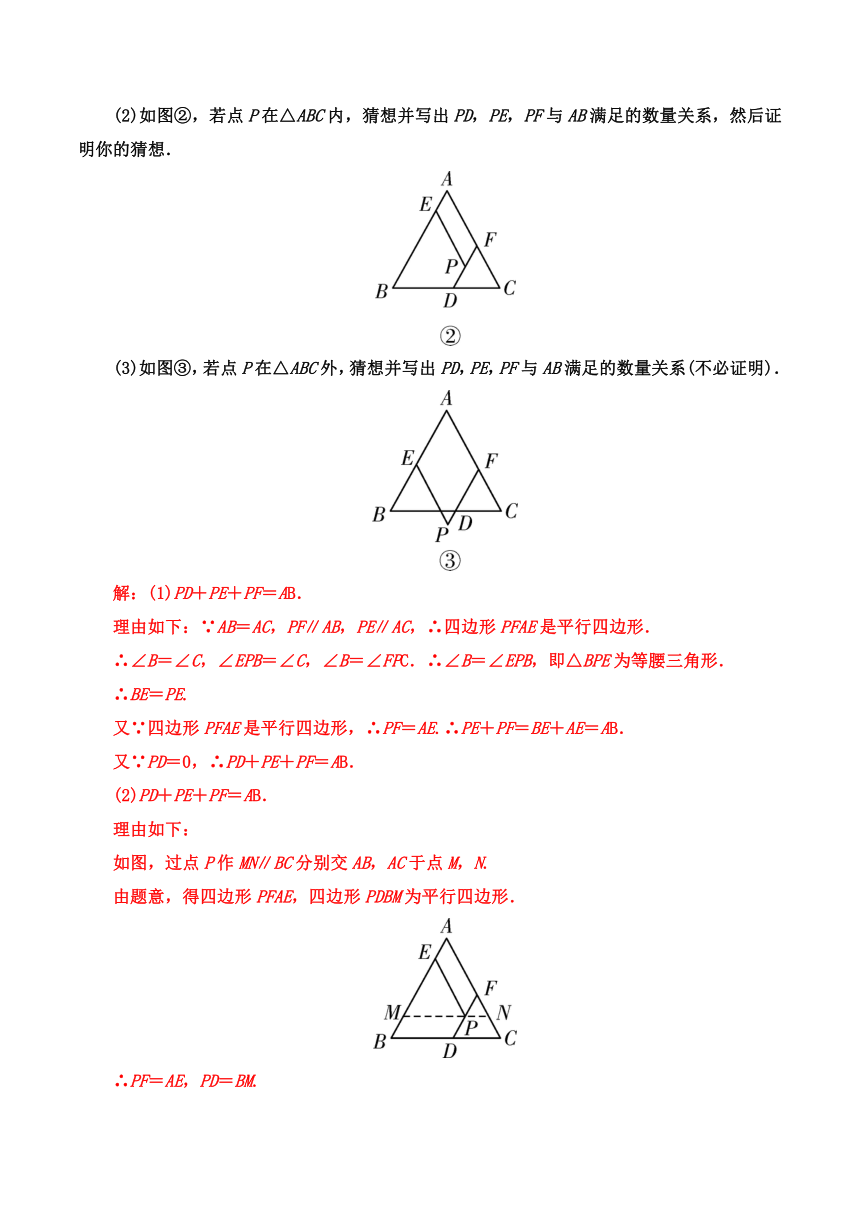
命题点一:利用多边形内(外)角和定理求边角问题
【思路点拨】
(1)多边形内角和定理:n边形的内角和为(n-2)×180°(n≥3)且n为整数.此公式推导的基本方法是从n边形的一个顶点出发引出(n-3)条对角线,将n边形分割为(n-2)个三角形,这(n-2)个三角形的所有内角之和正好是n边形的内角和.除此方法之外还有其他几种方法,但这些方法的基本思想是一样的.即将多边形转化为三角形,这也是研究多边形
(2)多边形的外角和等于360°.
①多边形的外角和指在每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.
②借助内角和和邻补角概念共同推出以下结论:外角和=180°n-180°(n-2)=360°.
例1一块正六边形硬纸片(如图①),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,见图②),需在每一个顶点处剪去一个四边形,例如图①中的四边形AGA′H,那么∠GA′H的大小是
60°
.
例2(保送生模拟题)E,F是四边形ABCD边AD,BC上的点,连结EF,将四边形ABFE沿直线EF折叠,使点A,点B落在四边形ABCD的内部,分别为A′,B′,再折叠将点D与点A′重合,折痕为GH,则下列结论一定正确的是( C )
A.∠1+∠2+∠3+∠4=2∠C
B.∠1+∠2+∠3+∠4=180°+∠C
C.∠1+∠2+∠3+∠4=360°-2∠C
D.∠1+∠2+∠3+∠4=540°-2∠C
命题点二:平行四边形的定义与性质
例3(2019·武汉期中改编)(1)在图①,②,③中,给出?ABCD的顶点A,B,D的坐标(如图所示),写出图①,②,③中的顶点C的坐标,它们分别是
(5,2)
,
(c+e,d)
,
(c+e-a,d)
.
(2)通过对图①,②,③,④的观察和顶点C的坐标的探究,你会发现:无论?ABCD处于直角坐标系中哪个位置,当其顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)时,则四个顶点的横坐标a,c,m,e之间的等量关系为
m+a=c+e
;纵坐标b,d,n,f之间的等量关系为
n+b=d+f
.
例4在△ABC中,AB=AC,P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
(1)如图①,若点P在BC边上,此时PD=0,猜想并写出PD,PE,PF与AB满足的数量关系,然后证明你的猜想.
(2)如图②,若点P在△ABC内,猜想并写出PD,PE,PF与AB满足的数量关系,然后证明你的猜想.
(3)如图③,若点P在△ABC外,猜想并写出PD,PE,PF与AB满足的数量关系(不必证明).
解:(1)PD+PE+PF=AB.
理由如下:∵AB=AC,PF∥AB,PE∥AC,∴四边形PFAE是平行四边形.
∴∠B=∠C,∠EPB=∠C,∠B=∠FPC.∴∠B=∠EPB,即△BPE为等腰三角形.
∴BE=PE.
又∵四边形PFAE是平行四边形,∴PF=AE.∴PE+PF=BE+AE=AB.
又∵PD=0,∴PD+PE+PF=AB.
(2)PD+PE+PF=AB.
理由如下:
如图,过点P作MN∥BC分别交AB,AC于点M,N.
由题意,得四边形PFAE,四边形PDBM为平行四边形.
∴PF=AE,PD=BM.
由题(1)的证明方法可同证△MEP为等腰三角形.
∴PE=ME.∴PD+PE+PF=BM+EM+AE=AB.
(3)PE+PF-PD=AB.
命题点三:利用平行四边形的性质解决边、角问题
【思路点拨】
本题考查的知识比较综合,包括平行四边形的性质、全等三角形的性质和判定以及等边三角形的性质.要解答本题,可以参照下面的思路:在等边三角形中,三条边相等,三个角都是60°,则可由60°角及平行四边形对角相等的性质可得∠DAE=∠1,即△DAE≌△FCD,得出DF=DE,同理可得出三条边都相等,进而可得出结论.
例5(浙江省自主招生模拟题)如图所示,在?ABCD中,△ABE和△BCF都是等边三角形.求证:△DEF是等边三角形.
证明:∵△ABE和△BCF都是等边三角形,且四边形ABCD是平行四边形.
∴AE=AB=CD,CF=BC=AD.
∴∠BAE=∠BCF=60°,
即∠DAE+∠BAD=∠1+∠BCD=60°.
在?ABCD中,∠BAD=∠BCD,
∴∠DAE=∠1.∴△DAE≌△FCD.∴DF=DE.
∵∠2=180°-∠ABE-∠CBF-∠BCD=60°-∠BCD,∠1=60°-∠BCD,
∴∠1=∠2=∠EAD.
∵EA=EB,AD=BC=BF,∴△BEF≌△AED.∴DE=EF.
∴DE=DF=EF,即△DEF为等边三角形.
例6如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,AN=MC,AM与BN相交于点P,求证:∠BPM=45°.
解:如图,过点M作ME∥AN,且ME=AN,连结NE,BE,则四边形AMEN为平行四边形,从而得到NE=AM,ME⊥BC.
∵ME=CM,∠EMB=∠MCA=90°,BM=AC,
∴△BEM≌△AMC.
∴BE=AM=NE,∠1=∠2,∠3=∠4.
∵∠1+∠3=90°,
∴∠2+∠4=90°,且BE=NE.
∴△BEN为等腰直角三角形,∠BNE=45°.
∵AM∥NE,∴∠BPM=∠BNE=45°.
命题点四:中心对称的应用
【思路点拨】
本题主要考查了轴对称图形和中心对称图形的作法,在解题过程中,正确理解轴对称图形和中心对称图形的概念是解题的关键.
例7如图,A,B,C是由三个相同的小正方形拼成的图形,请你再添加一个同样大小的小正方形(要求新添加的小正方形与原小正方形至少有一边重合),使所得的新图形分别为下列(1)(2)(3)题要求的图形,请画出示意图.
(1)是中心对称图形,但不是轴对称图形.
(2)是轴对称图形,但不是中心对称图形.
(3)既是中心对称图形,又是轴对称图形.
解:(1)如图①,取其中一个涂色的小正方形,则构成的图形是中心对称图形,但不是轴对称图形.
(2)如图②,取其中一个涂色的小正方形,则构成的图形是轴对称图形,但不是中心对称图形.
(3)如图③,在右边一个正方形上侧画一个正方形,则构成的图形既是轴对称图形,又是中心对称图形.
例8图①、图②均为7×6的正方形网格,点A,B,C在格点上.
(1)在图①中确定格点D,并画出以A,B,C,D为顶点的四边形,使其为轴对称图形(画一个即可).
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形(画一个即可).
解:(1)
(2)
课后练习
1.在?ABCD中,∠BAD的平分线AE
交BC于点E,且BE=3,若?ABCD的周长是16,则EC的长度是( A )
A.2
B.3 C.4
D.6
2.在凸四边形ABCD中,AB∥CD,且AB+BC=CD+AD,则( C )
A.AD>BC
B.ADC.AD=BC
D.AD与BC的大小关系不能确定
3.如图,在?ABCD中,∠ABC=75°,AF⊥BC于点F,AF交BD于点E.若DE=2AB,则∠AED的大小是( B )
A.60°
B.65°
C.70°
D.75°
4.(武汉市自主招生模拟题)如图,在?ABCD中,BC=2AB,CE⊥AB于点E,F为AD的中点,若∠AEF=54°,则∠B等于
( D )
A.54°
B.60°
C.66°
D.72°
5.如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为28
cm2,四边形ABCD的面积是18
cm2,则①②③④四个平行四边形周长的总和为( B )
A.72
cm
B.64
cm
C.56
cm
D.48
cm
6.如图,在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为( C )
A.2
B.3
C.4
D.5
7.如图,在△ABC中,AB=AC,AP=QP=QB=BC,则∠A=
20°
.
8.如图,?OABC的顶点A,C分别在直线x=1和x=4上,O为坐标原点,则对角线OB长的最小值为
5
.
9.在面积为15的?ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=5,BC=6,则CE+CF的值为 11+或1+ .
10.如图,在?ABCD中,∠ABC=60°,AE⊥AD交BD于点E,若DE=2DC,则∠DBC的大小是
20°
.
11.(2019·吉林省“城市杯”初中数学应用能力展示真题)如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为16,则BC+CD=
8
.
12.如图,在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,∠EAF=45°,且AE+AF=2,求?ABCD的周长.
解:∵∠EAF=45°,
∴∠C=360°-∠AEC-∠AFC-∠EAF=135°.
∴∠B=∠D=180°-∠C=45°.
∴AE=BE,AF=DF.
设AE=x,则AF=2-x.
在Rt△ABE中,根据勾股定理,得AB==x.
同理可得AD=(2-x)=4-x.
∴?ABCD的周长为2(AB+AD)=2(x+4-x)=8.
13.如图,一个凸六边形的六个内角都是120°,六条边长分别为a,b,c,d,e,f,则下列等式中成立的是( C )
A.a+b+c=d+e+f
B.a+c+e=b+d+f
C.a+b=d+e
D.a+c=b+d
14.如图,在?ABCD中,AB=BC=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,点A的对应点为A′.当CA′的长度最小时,CQ的长为是
7
.
15.在?ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图①中,证明CE=CF.
(2)若∠ABC=90°,G是EF的中点(如图②),直接写出∠BDG的度数.
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连结DB,DG(如图③),求∠BDG的度数.
解:(1)∵AF平分∠BAD,
∴∠BAF=∠DAF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠DAF=∠CEF,∠BAF=∠F.
∴∠CEF=∠F.
∴CE=CF.
(2)∠BDG=45°.
(3)如图,延长AB至点H,使AH=AD,连结DH,则△AHD是等边三角形.
∵∠ABC=120°,AF平分∠BAD,
∴∠DAF=∠BAF=30°,∠ADC=120°,∠DFA=30°.∴AD=DF.
∵AH=AD=DF,
∴BH=CF=CE=GF.
又∵FG∥CE,∠BCD=60°,
∴∠GFC=60°.
又∵∠BHD=∠GFD=60°,DH=DF,
∴△DBH≌△DGF,∠BDH=∠GDF.
∴∠BDG=∠ADC-∠ADB-∠GDF=∠ADC-
(∠ADB+∠BDH)=120°-60°=60°.
第1讲
命题点一:利用多边形内(外)角和定理求边角问题
【思路点拨】
(1)多边形内角和定理:n边形的内角和为(n-2)×180°(n≥3)且n为整数.此公式推导的基本方法是从n边形的一个顶点出发引出(n-3)条对角线,将n边形分割为(n-2)个三角形,这(n-2)个三角形的所有内角之和正好是n边形的内角和.除此方法之外还有其他几种方法,但这些方法的基本思想是一样的.即将多边形转化为三角形,这也是研究多边形
(2)多边形的外角和等于360°.
①多边形的外角和指在每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.
②借助内角和和邻补角概念共同推出以下结论:外角和=180°n-180°(n-2)=360°.
例1一块正六边形硬纸片(如图①),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,见图②),需在每一个顶点处剪去一个四边形,例如图①中的四边形AGA′H,那么∠GA′H的大小是
60°
.
例2(保送生模拟题)E,F是四边形ABCD边AD,BC上的点,连结EF,将四边形ABFE沿直线EF折叠,使点A,点B落在四边形ABCD的内部,分别为A′,B′,再折叠将点D与点A′重合,折痕为GH,则下列结论一定正确的是( C )
A.∠1+∠2+∠3+∠4=2∠C
B.∠1+∠2+∠3+∠4=180°+∠C
C.∠1+∠2+∠3+∠4=360°-2∠C
D.∠1+∠2+∠3+∠4=540°-2∠C
命题点二:平行四边形的定义与性质
例3(2019·武汉期中改编)(1)在图①,②,③中,给出?ABCD的顶点A,B,D的坐标(如图所示),写出图①,②,③中的顶点C的坐标,它们分别是
(5,2)
,
(c+e,d)
,
(c+e-a,d)
.
(2)通过对图①,②,③,④的观察和顶点C的坐标的探究,你会发现:无论?ABCD处于直角坐标系中哪个位置,当其顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)时,则四个顶点的横坐标a,c,m,e之间的等量关系为
m+a=c+e
;纵坐标b,d,n,f之间的等量关系为
n+b=d+f
.
例4在△ABC中,AB=AC,P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
(1)如图①,若点P在BC边上,此时PD=0,猜想并写出PD,PE,PF与AB满足的数量关系,然后证明你的猜想.
(2)如图②,若点P在△ABC内,猜想并写出PD,PE,PF与AB满足的数量关系,然后证明你的猜想.
(3)如图③,若点P在△ABC外,猜想并写出PD,PE,PF与AB满足的数量关系(不必证明).
解:(1)PD+PE+PF=AB.
理由如下:∵AB=AC,PF∥AB,PE∥AC,∴四边形PFAE是平行四边形.
∴∠B=∠C,∠EPB=∠C,∠B=∠FPC.∴∠B=∠EPB,即△BPE为等腰三角形.
∴BE=PE.
又∵四边形PFAE是平行四边形,∴PF=AE.∴PE+PF=BE+AE=AB.
又∵PD=0,∴PD+PE+PF=AB.
(2)PD+PE+PF=AB.
理由如下:
如图,过点P作MN∥BC分别交AB,AC于点M,N.
由题意,得四边形PFAE,四边形PDBM为平行四边形.
∴PF=AE,PD=BM.
由题(1)的证明方法可同证△MEP为等腰三角形.
∴PE=ME.∴PD+PE+PF=BM+EM+AE=AB.
(3)PE+PF-PD=AB.
命题点三:利用平行四边形的性质解决边、角问题
【思路点拨】
本题考查的知识比较综合,包括平行四边形的性质、全等三角形的性质和判定以及等边三角形的性质.要解答本题,可以参照下面的思路:在等边三角形中,三条边相等,三个角都是60°,则可由60°角及平行四边形对角相等的性质可得∠DAE=∠1,即△DAE≌△FCD,得出DF=DE,同理可得出三条边都相等,进而可得出结论.
例5(浙江省自主招生模拟题)如图所示,在?ABCD中,△ABE和△BCF都是等边三角形.求证:△DEF是等边三角形.
证明:∵△ABE和△BCF都是等边三角形,且四边形ABCD是平行四边形.
∴AE=AB=CD,CF=BC=AD.
∴∠BAE=∠BCF=60°,
即∠DAE+∠BAD=∠1+∠BCD=60°.
在?ABCD中,∠BAD=∠BCD,
∴∠DAE=∠1.∴△DAE≌△FCD.∴DF=DE.
∵∠2=180°-∠ABE-∠CBF-∠BCD=60°-∠BCD,∠1=60°-∠BCD,
∴∠1=∠2=∠EAD.
∵EA=EB,AD=BC=BF,∴△BEF≌△AED.∴DE=EF.
∴DE=DF=EF,即△DEF为等边三角形.
例6如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,AN=MC,AM与BN相交于点P,求证:∠BPM=45°.
解:如图,过点M作ME∥AN,且ME=AN,连结NE,BE,则四边形AMEN为平行四边形,从而得到NE=AM,ME⊥BC.
∵ME=CM,∠EMB=∠MCA=90°,BM=AC,
∴△BEM≌△AMC.
∴BE=AM=NE,∠1=∠2,∠3=∠4.
∵∠1+∠3=90°,
∴∠2+∠4=90°,且BE=NE.
∴△BEN为等腰直角三角形,∠BNE=45°.
∵AM∥NE,∴∠BPM=∠BNE=45°.
命题点四:中心对称的应用
【思路点拨】
本题主要考查了轴对称图形和中心对称图形的作法,在解题过程中,正确理解轴对称图形和中心对称图形的概念是解题的关键.
例7如图,A,B,C是由三个相同的小正方形拼成的图形,请你再添加一个同样大小的小正方形(要求新添加的小正方形与原小正方形至少有一边重合),使所得的新图形分别为下列(1)(2)(3)题要求的图形,请画出示意图.
(1)是中心对称图形,但不是轴对称图形.
(2)是轴对称图形,但不是中心对称图形.
(3)既是中心对称图形,又是轴对称图形.
解:(1)如图①,取其中一个涂色的小正方形,则构成的图形是中心对称图形,但不是轴对称图形.
(2)如图②,取其中一个涂色的小正方形,则构成的图形是轴对称图形,但不是中心对称图形.
(3)如图③,在右边一个正方形上侧画一个正方形,则构成的图形既是轴对称图形,又是中心对称图形.
例8图①、图②均为7×6的正方形网格,点A,B,C在格点上.
(1)在图①中确定格点D,并画出以A,B,C,D为顶点的四边形,使其为轴对称图形(画一个即可).
(2)在图②中确定格点E,并画出以A,B,C,E为顶点的四边形,使其为中心对称图形(画一个即可).
解:(1)
(2)
课后练习
1.在?ABCD中,∠BAD的平分线AE
交BC于点E,且BE=3,若?ABCD的周长是16,则EC的长度是( A )
A.2
B.3 C.4
D.6
2.在凸四边形ABCD中,AB∥CD,且AB+BC=CD+AD,则( C )
A.AD>BC
B.AD
D.AD与BC的大小关系不能确定
3.如图,在?ABCD中,∠ABC=75°,AF⊥BC于点F,AF交BD于点E.若DE=2AB,则∠AED的大小是( B )
A.60°
B.65°
C.70°
D.75°
4.(武汉市自主招生模拟题)如图,在?ABCD中,BC=2AB,CE⊥AB于点E,F为AD的中点,若∠AEF=54°,则∠B等于
( D )
A.54°
B.60°
C.66°
D.72°
5.如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为28
cm2,四边形ABCD的面积是18
cm2,则①②③④四个平行四边形周长的总和为( B )
A.72
cm
B.64
cm
C.56
cm
D.48
cm
6.如图,在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为( C )
A.2
B.3
C.4
D.5
7.如图,在△ABC中,AB=AC,AP=QP=QB=BC,则∠A=
20°
.
8.如图,?OABC的顶点A,C分别在直线x=1和x=4上,O为坐标原点,则对角线OB长的最小值为
5
.
9.在面积为15的?ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=5,BC=6,则CE+CF的值为 11+或1+ .
10.如图,在?ABCD中,∠ABC=60°,AE⊥AD交BD于点E,若DE=2DC,则∠DBC的大小是
20°
.
11.(2019·吉林省“城市杯”初中数学应用能力展示真题)如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为16,则BC+CD=
8
.
12.如图,在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,∠EAF=45°,且AE+AF=2,求?ABCD的周长.
解:∵∠EAF=45°,
∴∠C=360°-∠AEC-∠AFC-∠EAF=135°.
∴∠B=∠D=180°-∠C=45°.
∴AE=BE,AF=DF.
设AE=x,则AF=2-x.
在Rt△ABE中,根据勾股定理,得AB==x.
同理可得AD=(2-x)=4-x.
∴?ABCD的周长为2(AB+AD)=2(x+4-x)=8.
13.如图,一个凸六边形的六个内角都是120°,六条边长分别为a,b,c,d,e,f,则下列等式中成立的是( C )
A.a+b+c=d+e+f
B.a+c+e=b+d+f
C.a+b=d+e
D.a+c=b+d
14.如图,在?ABCD中,AB=BC=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,点A的对应点为A′.当CA′的长度最小时,CQ的长为是
7
.
15.在?ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图①中,证明CE=CF.
(2)若∠ABC=90°,G是EF的中点(如图②),直接写出∠BDG的度数.
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连结DB,DG(如图③),求∠BDG的度数.
解:(1)∵AF平分∠BAD,
∴∠BAF=∠DAF.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠DAF=∠CEF,∠BAF=∠F.
∴∠CEF=∠F.
∴CE=CF.
(2)∠BDG=45°.
(3)如图,延长AB至点H,使AH=AD,连结DH,则△AHD是等边三角形.
∵∠ABC=120°,AF平分∠BAD,
∴∠DAF=∠BAF=30°,∠ADC=120°,∠DFA=30°.∴AD=DF.
∵AH=AD=DF,
∴BH=CF=CE=GF.
又∵FG∥CE,∠BCD=60°,
∴∠GFC=60°.
又∵∠BHD=∠GFD=60°,DH=DF,
∴△DBH≌△DGF,∠BDH=∠GDF.
∴∠BDG=∠ADC-∠ADB-∠GDF=∠ADC-
(∠ADB+∠BDH)=120°-60°=60°.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
