2.1.2 有理数的加法教学课件(共26张PPT)
文档属性
| 名称 | 2.1.2 有理数的加法教学课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-14 19:02:42 | ||
图片预览







文档简介
有理数的加法二
1、同号两数相加,取相同的符号,并把绝对值相加.
2、异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
3、互为相反数的两个数相加得0.
4、一个数同0相加,仍得这个数.
有理数加法法则
知识回顾
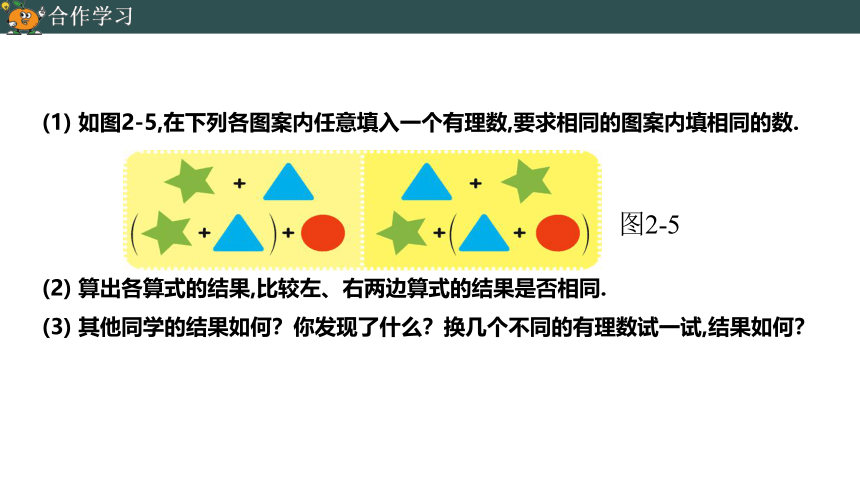
(1) 如图2-5,在下列各图案内任意填入一个有理数,要求相同的图案内填相同的数.
(2) 算出各算式的结果,比较左、右两边算式的结果是否相同.
(3) 其他同学的结果如何?你发现了什么?换几个不同的有理数试一试,结果如何?
合作学习
在有理数运算中,加法的交换律和结合律仍成立:
加法交换律:两个数相加,交换加数的位置,和不变.
a+b=b+a.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
(a+b)+c=a+(b+c).
合作学习
例3 计算:
(1)15+(-13)+18;
(2)(-2.48)+4.33+(-7.52)+(-4.33);
(3) .
解:(1)原式=15+18+(-13)
=33+(-13)
=20
=(15+18)+(-13)
加法交换律
加法结合律
(2)原式=(-2.48)+(-7.52)+(+4.33)+(-4.33)
=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
例题讲解
(3)原式=
=
=
例3 计算:
(1)15+(-13)+18;
(2)(-2.48)+4.33+(-7.52)+(-4.33);
(3)
例题讲解
使用运算律通常有下列几种方法:
(1)能凑整的先凑整简称凑整结合法;
(2)把正数与负数分别结合在一起再相加简称同号结合法;
(3)有相反数的先把相反数相加简称相反数结合法;
(4)遇到分数,先把同分母的数相加,简称同分母结合法.
归纳
(1)(-1.6)+(+2.3)+(-3.4)+(-12.7);
(2)(+11)+(-15)+(+6)+(-13);
(3)(+17)+(-30)+(-17)+(+30);
(4)
能凑整的数先相加
符号相同的数先相加
互为相反数先相加(凑0)
分母相同的数先相加
看谁算得快!
变式训练
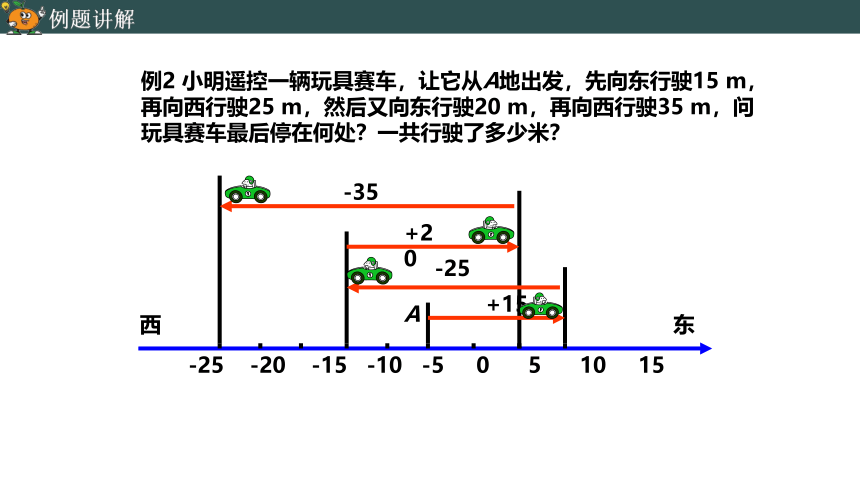
例2 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
A
-25 -20 -15 -10 -5 0 5 10 15
东
西
+15
-25
-35
+20
例题讲解
解:向东记为正,根据题意得:
(+15)+(-25)+(+20)+(-35)
=(15+20)+[(-25)+(-35)]
=-25(m);
|+15|+|-25|+|+20|+|-35|
=15+25+20+35
=95(m).
答:小明的遥控车最后停在小明的西边25 m处,一共行驶了95 m.
例题讲解
某升降机第一次上升8米,第二次又上升6米,第三次下降7米,第四次又下降了9米,这时升降机在初试位置的什么位置?升降机共运行了多少米?
解:向上记为正,向下记为负,根据题意,得
(+8)+(+6)+(-7)+(-9)=-2(m);
|+8|+|+6|+|-7|+|-9|=30(m).
答:这时升降机在初试位置的下方2 m处,升降机共运行了30 m.
变式训练
1. 计算(-20)+3????????+20+(-???????? ) ,比较合适的做法是( )
A. 把一、三两个加数结合,二、四两个加数结合
B. 把一、二两个加数结合,三、四两个加数结合
C. 把一、四两个加数结合,二、三两个加数结合
D. 把一、二、四这三个加数先结合
?
课堂练习
2、下列各式中正确利用了加法运算律的是( )
A.(+5)+(-7)+(-5)=(+5)+(-5)+(-7)
B.
C.(-1)+(-2)+(+3)=(-3)+(+l)+(-2)
D.(-1.5)+(+2.5)=(-2.5)+(+1.5)
课堂练习
3. 李老师的银行卡中有5500元,取出1800元,又存入1500元,又取出2200元,这时银行卡中还有 元钱.
3000
课堂练习
4.(1)(+26)+(﹣14)+(﹣16)+(+8).
(1)解:原式=(+26)+(+8)+(﹣14)+(﹣16)
=34+(﹣30)
=4.
课堂练习
4.(1)(+26)+(﹣14)+(﹣16)+(+8).
课堂练习
5.7箱橘子,标准质量为每箱15千克,每箱与标准质量差值如下(单位:千克,超过的用正数表示,不足的用负数表示):0.3,﹣0.4,0.25,﹣0.2,﹣0.7,1.1,﹣1,称得总质量与总标准质量相比超过或不足多少千克?7箱橘子共有多少千克?
【分析】利用有理数的加法法则把0.3,﹣0.4,0.25,﹣0.2,﹣0.7,1.1,﹣1,相加即可得到与总标准质量相比超过或不足的千克数,然后再利用15千克×7箱,然后再加上比超过或不足的千克数.
课堂练习
5.7箱橘子,标准质量为每箱15千克,每箱与标准质量差值如下(单位:千克,超过的用正数表示,不足的用负数表示):0.3,﹣0.4,0.25,﹣0.2,﹣0.7,1.1,﹣1,称得总质量与总标准质量相比超过或不足多少千克?7箱橘子共有多少千克?
解:0.3+0.25+1.1﹣0.4﹣0.2﹣0.7﹣1=﹣0.65(千克),
15×7﹣0.65=104.35(千克),
答:不足0.65千克,共104.35千克.
课堂练习
6.有6筐蔬菜,每筐质量分别为(单位:kg):
48,52,47,49,53,54.
(1)如果以50kg为基准,超过的千克数记为正数,不足的千克数记为负数,则用正、负数表示这6筐蔬菜的质量分别为(单位:kg):
_____,_____,_____,_____,_____,_____;
(2)试用两种不同的方法求出这6筐蔬菜的总质量.
-2
+2
-3
-1
+3
+4
解:(2)方法一:48+52+47+49+53+54=303;
方法二:
(-2)+(+2)+(-3)+(-1)+(+3)+(+4)=3
50×6 +3 =300+3=303
答:这6筐蔬菜的总质量是303kg.
课堂练习
7、在-49,-48,… , 0,1,2, …,2008,2009这一串连续整数中,前100个数的和是多少?
解:根据题意得:前100个连续整数为-49、-48、-47,…,-1,0,1,…49,50,
之和为:
(-49)+(-48)+(-47)+…+0+1+…+49+50 =50.
课堂练习
8. 某电动车厂本周计划每天生产电动车400辆,由于人数和操作的原因,每天实际生产量分别为405辆,393辆,397辆,410辆,391辆,385辆和405辆.
(1)用正、负数表示每天实际生产量与计划量相比的增减情况;
(2)该厂本周实际共生产多少辆电动车?
解:(1)把超过计划量的车的辆数记为正,低于计划量的车的辆数记为负,
可分别表示为+5,-7,-3,+10,-9,-15,+5.
课堂练习
8. 某电动车厂本周计划每天生产电动车400辆,由于人数和操作的原因,每天实际生产量分别为405辆,393辆,397辆,410辆,391辆,385辆和405辆.
(1)用正、负数表示每天实际生产量与计划量相比的增减情况;
(2)该厂本周实际共生产多少辆电动车?
(2)本周总增减量为(+5)+(-7)+(-3)+(+10)+(-9)+(-15)+(+5)
=[(+5)+(+10)+(+5)]+[(-7)+(-3)+(-9)+(-15)]
=20+(-34)=-14.
因此,该厂本周实际共产生电动车400×7+(-14)=2786(辆).
课堂练习
两个数相加的和,在什么条件下大于其中任何一个加数?在什么条件下等于其中任何一个加数?在什么条件下小于其中任何一个加数?
当两个加数都是正数时,和大于任何一个加数;
当两个加数都是 0 时,和等于任何一个加数;
当两个加数都是负数时,和小于任何一个加数.
归纳
一、加法的运算律
1、加法交换律:两个数相加,交换加数的位置,和不变.a+b=b+a
2、加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.(a+b)+c=a+(b+c)
二、使用运算律通常有下列几种方法:
(1)凑整结合法;
(2)同号结合法;
(3)相反数结合法;
(4)同分母结合法.
课堂总结
教材练习题
课后作业
谢
谢
观
看
1、同号两数相加,取相同的符号,并把绝对值相加.
2、异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
3、互为相反数的两个数相加得0.
4、一个数同0相加,仍得这个数.
有理数加法法则
知识回顾
(1) 如图2-5,在下列各图案内任意填入一个有理数,要求相同的图案内填相同的数.
(2) 算出各算式的结果,比较左、右两边算式的结果是否相同.
(3) 其他同学的结果如何?你发现了什么?换几个不同的有理数试一试,结果如何?
合作学习
在有理数运算中,加法的交换律和结合律仍成立:
加法交换律:两个数相加,交换加数的位置,和不变.
a+b=b+a.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
(a+b)+c=a+(b+c).
合作学习
例3 计算:
(1)15+(-13)+18;
(2)(-2.48)+4.33+(-7.52)+(-4.33);
(3) .
解:(1)原式=15+18+(-13)
=33+(-13)
=20
=(15+18)+(-13)
加法交换律
加法结合律
(2)原式=(-2.48)+(-7.52)+(+4.33)+(-4.33)
=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
例题讲解
(3)原式=
=
=
例3 计算:
(1)15+(-13)+18;
(2)(-2.48)+4.33+(-7.52)+(-4.33);
(3)
例题讲解
使用运算律通常有下列几种方法:
(1)能凑整的先凑整简称凑整结合法;
(2)把正数与负数分别结合在一起再相加简称同号结合法;
(3)有相反数的先把相反数相加简称相反数结合法;
(4)遇到分数,先把同分母的数相加,简称同分母结合法.
归纳
(1)(-1.6)+(+2.3)+(-3.4)+(-12.7);
(2)(+11)+(-15)+(+6)+(-13);
(3)(+17)+(-30)+(-17)+(+30);
(4)
能凑整的数先相加
符号相同的数先相加
互为相反数先相加(凑0)
分母相同的数先相加
看谁算得快!
变式训练
例2 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
A
-25 -20 -15 -10 -5 0 5 10 15
东
西
+15
-25
-35
+20
例题讲解
解:向东记为正,根据题意得:
(+15)+(-25)+(+20)+(-35)
=(15+20)+[(-25)+(-35)]
=-25(m);
|+15|+|-25|+|+20|+|-35|
=15+25+20+35
=95(m).
答:小明的遥控车最后停在小明的西边25 m处,一共行驶了95 m.
例题讲解
某升降机第一次上升8米,第二次又上升6米,第三次下降7米,第四次又下降了9米,这时升降机在初试位置的什么位置?升降机共运行了多少米?
解:向上记为正,向下记为负,根据题意,得
(+8)+(+6)+(-7)+(-9)=-2(m);
|+8|+|+6|+|-7|+|-9|=30(m).
答:这时升降机在初试位置的下方2 m处,升降机共运行了30 m.
变式训练
1. 计算(-20)+3????????+20+(-???????? ) ,比较合适的做法是( )
A. 把一、三两个加数结合,二、四两个加数结合
B. 把一、二两个加数结合,三、四两个加数结合
C. 把一、四两个加数结合,二、三两个加数结合
D. 把一、二、四这三个加数先结合
?
课堂练习
2、下列各式中正确利用了加法运算律的是( )
A.(+5)+(-7)+(-5)=(+5)+(-5)+(-7)
B.
C.(-1)+(-2)+(+3)=(-3)+(+l)+(-2)
D.(-1.5)+(+2.5)=(-2.5)+(+1.5)
课堂练习
3. 李老师的银行卡中有5500元,取出1800元,又存入1500元,又取出2200元,这时银行卡中还有 元钱.
3000
课堂练习
4.(1)(+26)+(﹣14)+(﹣16)+(+8).
(1)解:原式=(+26)+(+8)+(﹣14)+(﹣16)
=34+(﹣30)
=4.
课堂练习
4.(1)(+26)+(﹣14)+(﹣16)+(+8).
课堂练习
5.7箱橘子,标准质量为每箱15千克,每箱与标准质量差值如下(单位:千克,超过的用正数表示,不足的用负数表示):0.3,﹣0.4,0.25,﹣0.2,﹣0.7,1.1,﹣1,称得总质量与总标准质量相比超过或不足多少千克?7箱橘子共有多少千克?
【分析】利用有理数的加法法则把0.3,﹣0.4,0.25,﹣0.2,﹣0.7,1.1,﹣1,相加即可得到与总标准质量相比超过或不足的千克数,然后再利用15千克×7箱,然后再加上比超过或不足的千克数.
课堂练习
5.7箱橘子,标准质量为每箱15千克,每箱与标准质量差值如下(单位:千克,超过的用正数表示,不足的用负数表示):0.3,﹣0.4,0.25,﹣0.2,﹣0.7,1.1,﹣1,称得总质量与总标准质量相比超过或不足多少千克?7箱橘子共有多少千克?
解:0.3+0.25+1.1﹣0.4﹣0.2﹣0.7﹣1=﹣0.65(千克),
15×7﹣0.65=104.35(千克),
答:不足0.65千克,共104.35千克.
课堂练习
6.有6筐蔬菜,每筐质量分别为(单位:kg):
48,52,47,49,53,54.
(1)如果以50kg为基准,超过的千克数记为正数,不足的千克数记为负数,则用正、负数表示这6筐蔬菜的质量分别为(单位:kg):
_____,_____,_____,_____,_____,_____;
(2)试用两种不同的方法求出这6筐蔬菜的总质量.
-2
+2
-3
-1
+3
+4
解:(2)方法一:48+52+47+49+53+54=303;
方法二:
(-2)+(+2)+(-3)+(-1)+(+3)+(+4)=3
50×6 +3 =300+3=303
答:这6筐蔬菜的总质量是303kg.
课堂练习
7、在-49,-48,… , 0,1,2, …,2008,2009这一串连续整数中,前100个数的和是多少?
解:根据题意得:前100个连续整数为-49、-48、-47,…,-1,0,1,…49,50,
之和为:
(-49)+(-48)+(-47)+…+0+1+…+49+50 =50.
课堂练习
8. 某电动车厂本周计划每天生产电动车400辆,由于人数和操作的原因,每天实际生产量分别为405辆,393辆,397辆,410辆,391辆,385辆和405辆.
(1)用正、负数表示每天实际生产量与计划量相比的增减情况;
(2)该厂本周实际共生产多少辆电动车?
解:(1)把超过计划量的车的辆数记为正,低于计划量的车的辆数记为负,
可分别表示为+5,-7,-3,+10,-9,-15,+5.
课堂练习
8. 某电动车厂本周计划每天生产电动车400辆,由于人数和操作的原因,每天实际生产量分别为405辆,393辆,397辆,410辆,391辆,385辆和405辆.
(1)用正、负数表示每天实际生产量与计划量相比的增减情况;
(2)该厂本周实际共生产多少辆电动车?
(2)本周总增减量为(+5)+(-7)+(-3)+(+10)+(-9)+(-15)+(+5)
=[(+5)+(+10)+(+5)]+[(-7)+(-3)+(-9)+(-15)]
=20+(-34)=-14.
因此,该厂本周实际共产生电动车400×7+(-14)=2786(辆).
课堂练习
两个数相加的和,在什么条件下大于其中任何一个加数?在什么条件下等于其中任何一个加数?在什么条件下小于其中任何一个加数?
当两个加数都是正数时,和大于任何一个加数;
当两个加数都是 0 时,和等于任何一个加数;
当两个加数都是负数时,和小于任何一个加数.
归纳
一、加法的运算律
1、加法交换律:两个数相加,交换加数的位置,和不变.a+b=b+a
2、加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.(a+b)+c=a+(b+c)
二、使用运算律通常有下列几种方法:
(1)凑整结合法;
(2)同号结合法;
(3)相反数结合法;
(4)同分母结合法.
课堂总结
教材练习题
课后作业
谢
谢
观
看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
