4.1 比例线段 黄金分割+4.2 平行线分线段成比例配套练习(含解析)
文档属性
| 名称 | 4.1 比例线段 黄金分割+4.2 平行线分线段成比例配套练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-15 15:26:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.1比例线段黄金分割+4.2平行线分线段成比例练习(含解析)
一.选择题(共15小题)
1.(2019秋?越秀区期末)已知a=2b,那么下列等式中不一定成立的是( )
A.a+b=3b B.a﹣c=2b﹣c C.a=b D.=2
2.(2020春?万州区期末)若==,则的值是( )
A. B.﹣ C.﹣16 D.﹣
3.(2020春?芝罘区期中)在比例尺是1:200000的地图上,A、B两地间的距离为4cm,则A、B两地的实际距离是( )
A.8km B.5km C.80km D.0.5km
4.(2020?临潭县校级模拟)下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
5.(2020春?常熟市期末)点B是线段AC的黄金分割点,且AB<BC,若AC=2,则BC的长为( )
A. B. C.+1 D.﹣1
6.(2019秋?沙坪坝区校级期末)黄金分割数是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算2(﹣1)的值( )
A.在1和2之间 B.在2和3之间 C.在3和4之间 D.在4和5之间
7.(2020?金昌)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
8.(2019秋?杨浦区校级月考)直线DE交△ABC中的AB于D点,交AC于E点,那么能推出DE∥BC的条件是( )
A. B.
C. D.
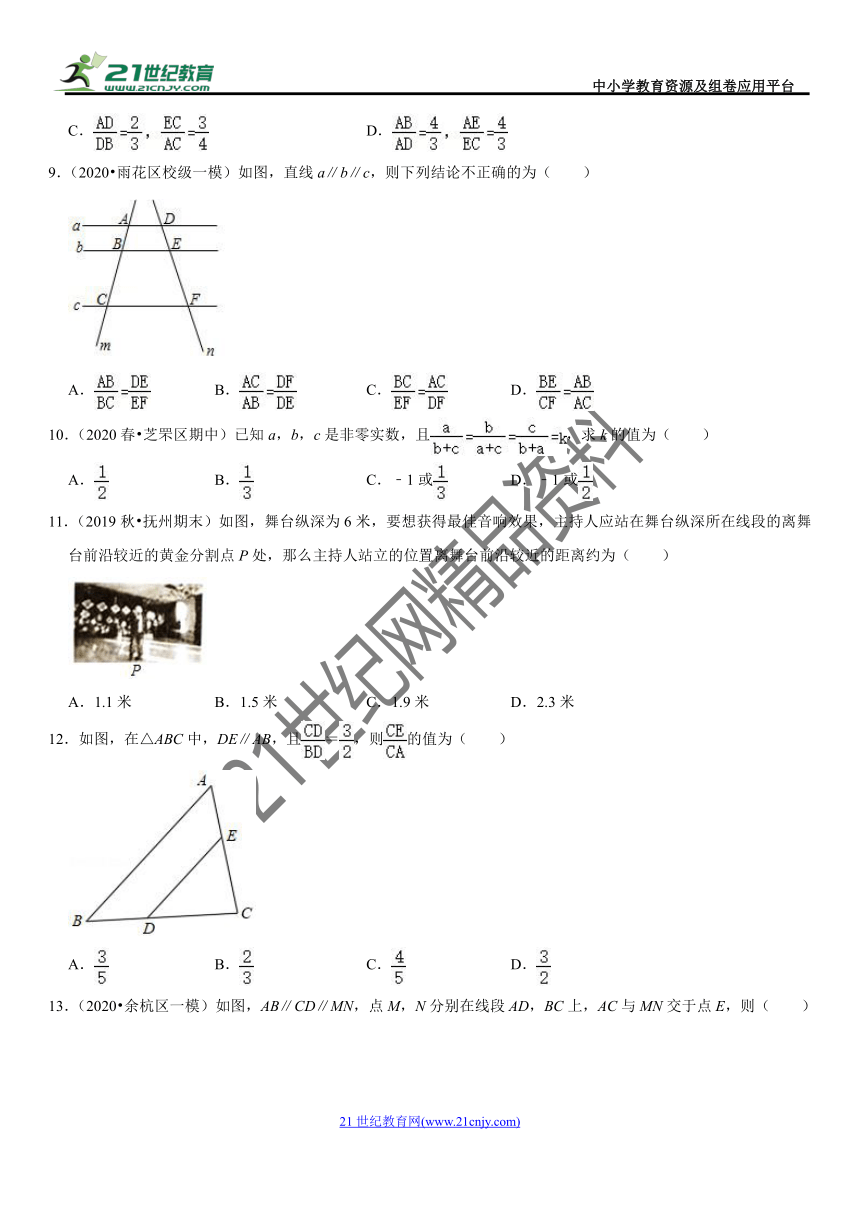
9.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
10.(2020春?芝罘区期中)已知a,b,c是非零实数,且,求k的值为( )
A. B. C.﹣1或 D.﹣1或
11.(2019秋?抚州期末)如图,舞台纵深为6米,要想获得最佳音响效果,主持人应站在舞台纵深所在线段的离舞台前沿较近的黄金分割点P处,那么主持人站立的位置离舞台前沿较近的距离约为( )
A.1.1米 B.1.5米 C.1.9米 D.2.3米
12.如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
13.(2020?余杭区一模)如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E,则( )
A.= B.= C.= D.=
14.(2019春?朝阳区校级月考)如图,直线L1∥L2∥L3,直线L1、L2、L3分别和直线m交于点A、B、C,和直线n交于点A1、B1、C1.若AB=6,AC=9,A1B1=8,则线段B1C1的长为( )
A.2 B.3 C.4 D.5
15.(2019?凉山州)如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=( )
A.1:2 B.1:3 C.1:4 D.2:3
二.填空题(共8小题)
16.(2020?庐阳区校级一模)已知,则的值为 .
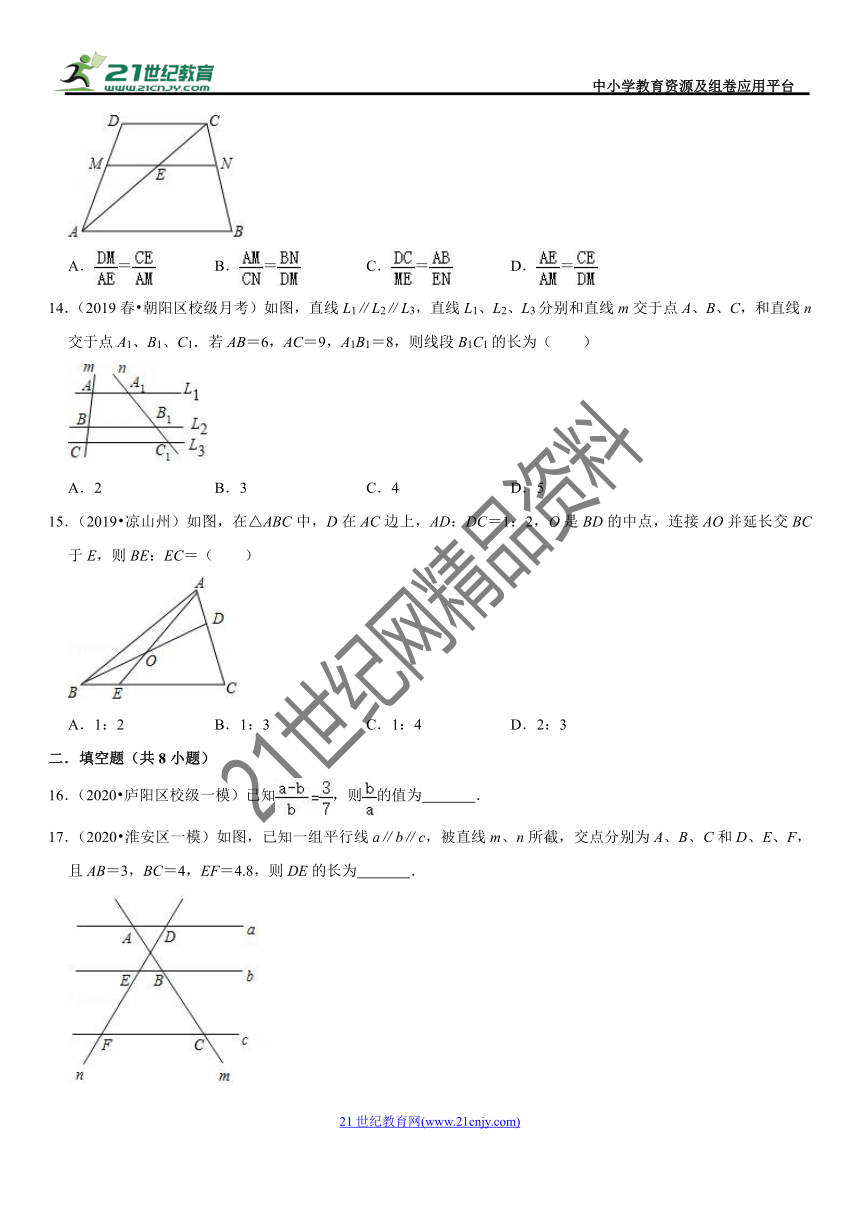
17.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 .
18.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= .
19.(2019秋?海陵区期末)如图,E是?ABCD的BC边的中点,BD与AE相交于F,则△ABF与四边形ECDF的面积之比等于 .
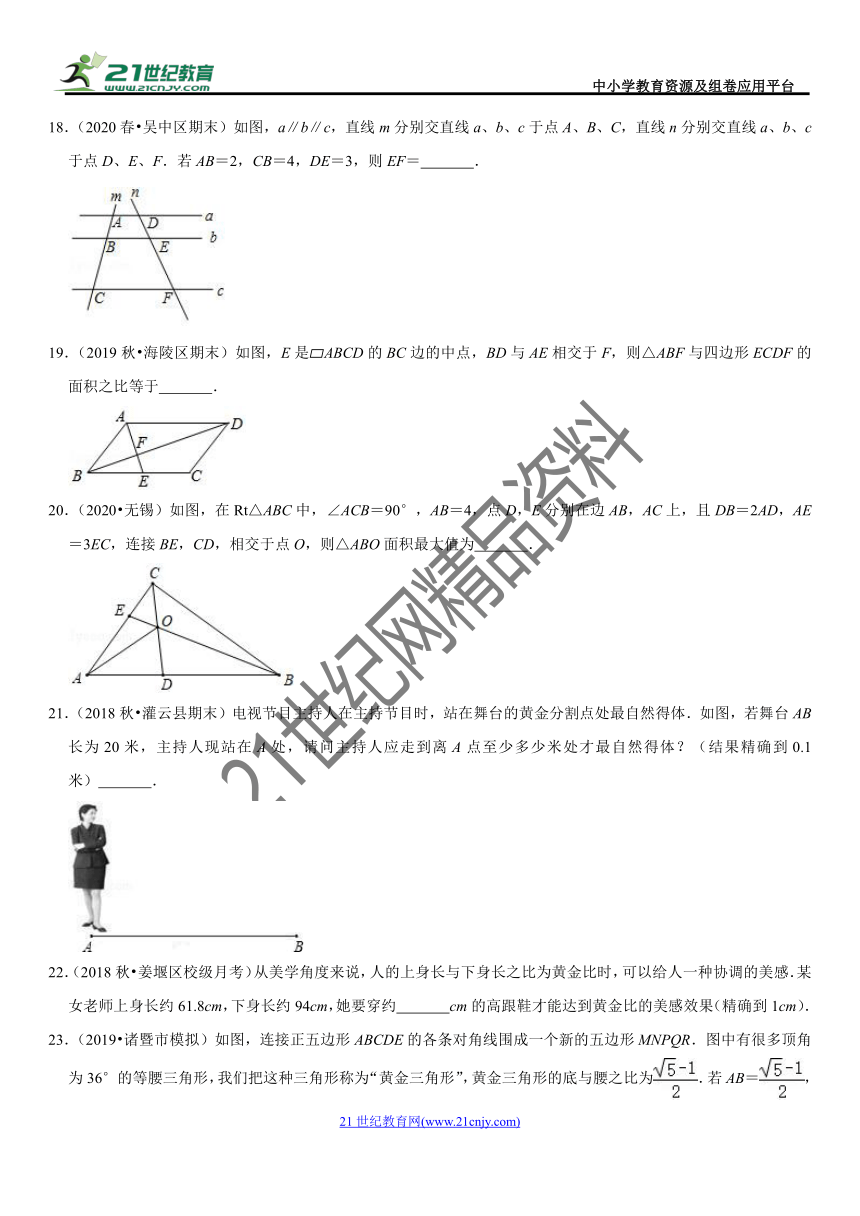
20.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
21.(2018秋?灌云县期末)电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB长为20米,主持人现站在A处,请问主持人应走到离A点至少多少米处才最自然得体?(结果精确到0.1米) .
22.(2018秋?姜堰区校级月考)从美学角度来说,人的上身长与下身长之比为黄金比时,可以给人一种协调的美感.某女老师上身长约61.8cm,下身长约94cm,她要穿约 cm的高跟鞋才能达到黄金比的美感效果(精确到1cm).
23.(2019?诸暨市模拟)如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若AB=,则MN= .
三.解答题(共9小题)
24.(2018秋?霍邱县期末)已知a:b:c=2:3:4,且2a+3b﹣2c=15,求a,b,c的值.
25.(2019秋?昭平县期中)已知:线段a、b、c,且==.
(1)求的值.
(2)如线段a、b、c满足a+b+c=27,求a﹣b+c的值.
26.(2019?思明区校级模拟)如图,点C将线段AB分成两部分,若AC2=BC?AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
27.(2017秋?霍邱县期末)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC?CD的大小关系;
(2)求证:△ABC∽△BDC.
28.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
29.(2019秋?长安区校级月考)如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
30.(2018秋?虹口区期中)如图,已知AD∥BE∥CF,它们依次交直线l1,l2于点A、B、C和点D、E、F,=,AC=10.
(1)求AB,BC的长;
(2)如果AD=7,CF=12,求BE的长.
31.(2018秋?长春期中)探究:如图①,在△ABC中,点D是BC的中点,点E在AB上,且=.过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,求的值.
应用:如图②,在△ABC中,点D是BC上的点=,点E在AB上,且=,过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,则= .
4.14.2参考答案与试题解析
一.选择题(共15小题)
1.(2019秋?越秀区期末)已知a=2b,那么下列等式中不一定成立的是( )
A.a+b=3b B.a﹣c=2b﹣c C.a=b D.=2
【解答】解:A、∵a=2b,∴a+b=3b,成立,不合题意;
B、∵a=2b,∴a﹣c=2b﹣c,成立,不合题意;
C、∵a=2b,∴a=b,成立,不合题意;
D、∵a=2b,∴=2(b≠0),原式不一定成立,符合题意.
故选:D.
2.(2020春?万州区期末)若==,则的值是( )
A. B.﹣ C.﹣16 D.﹣
【解答】解:∵==,
∴设a=2x,则b=3x,c=4x,
故原式=
=
=﹣.
故选:B.
3.(2020春?芝罘区期中)在比例尺是1:200000的地图上,A、B两地间的距离为4cm,则A、B两地的实际距离是( )
A.8km B.5km C.80km D.0.5km
【解答】解:设A、B两地的实际距离为xcm,
∵比例尺为1:200000,
∴4:x=1:200000,
∴x=800000,
800000cm=8km.
故选:A.
4.(2020?临潭县校级模拟)下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
【解答】解:A、∵2×5≠3×4,∴选项A不成比例;
B、∵2×8≠4×6,∴选项B不成比例;
C、∵3×12≠6×8,∴选项C不成比例;
D、∵1×15=3×5,∴选项D成比例.
故选:D.
5.(2020春?常熟市期末)点B是线段AC的黄金分割点,且AB<BC,若AC=2,则BC的长为( )
A. B. C.+1 D.﹣1
【解答】解:∵点B是线段AC的黄金分割点,且AB<BC,
∴BC=AC,
∵AC=2,
∴BC=﹣1.
故选:D.
6.(2019秋?沙坪坝区校级期末)黄金分割数是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算2(﹣1)的值( )
A.在1和2之间 B.在2和3之间 C.在3和4之间 D.在4和5之间
【解答】解:∵<,
又∵2(﹣1)=2﹣2,
∴4<2<5,
∴2<2﹣2<3,
∴2(﹣1)的值在2和3之间;
故选:B.
7.(2020?金昌)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
【解答】解:∵雕像的腰部以下a与全身b的高度比值接近0.618,
∴≈0.618,
∵b为2米,
∴a约为1.24米.
故选:A.
8.(2019秋?杨浦区校级月考)直线DE交△ABC中的AB于D点,交AC于E点,那么能推出DE∥BC的条件是( )
A. B.
C. D.
【解答】解:A.由不能得到对应线段成比例,即不能推出DE∥BC,不合题意;
B.由可得到对应线段成比例,即可推出DE∥BC,符合题意;
C.由不能得到对应线段成比例,即不能推出DE∥BC,不合题意;
D.由不能得到对应线段成比例,即不能推出DE∥BC,不合题意;
故选:B.
9.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
【解答】解:A、∵a∥b∥c,
∴=,本选项结论正确,不符合题意;
B、∵a∥b∥c,
∴=,本选项结论正确,不符合题意;
C、∵a∥b∥c,
∴=,本选项结论正确,不符合题意;
D、连接AF,交BE于H,
∵b∥c,
∴△ABH∽△ACF,
∴=≠,本选项结论不正确,符合题意;
故选:D.
10.(2020春?芝罘区期中)已知a,b,c是非零实数,且,求k的值为( )
A. B. C.﹣1或 D.﹣1或
【解答】解:∵,
∴a=(b+c)k,b=(a+c)k,c=(a+b)k,
∴a+b+c=2(a+b+c)k,
∴①当a+b+c≠0时,k=,
②当a+b+c=0时,a=﹣(b+c),
k==﹣1,
综上所述:k=﹣1或.
故选:D.
11.(2019秋?抚州期末)如图,舞台纵深为6米,要想获得最佳音响效果,主持人应站在舞台纵深所在线段的离舞台前沿较近的黄金分割点P处,那么主持人站立的位置离舞台前沿较近的距离约为( )
A.1.1米 B.1.5米 C.1.9米 D.2.3米
【解答】解:∵节目主持人应站在舞台的黄金分割处,
∴距前沿较近的距离 6×=9﹣3≈2.3(米),
故选:D.
12.如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
【解答】解:∵DE∥AB,
∴==,
∴的值为,
故选:A.
13.(2020?余杭区一模)如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E,则( )
A.= B.= C.= D.=
【解答】解:∵ME∥CD,
∴=,
∴=.
故选:D.
14.(2019春?朝阳区校级月考)如图,直线L1∥L2∥L3,直线L1、L2、L3分别和直线m交于点A、B、C,和直线n交于点A1、B1、C1.若AB=6,AC=9,A1B1=8,则线段B1C1的长为( )
A.2 B.3 C.4 D.5
【解答】解:∵直线L1∥L2∥L3,
∴=,
∵AB=6,AC=9,
∴BC=3,
∴=,
∴B1C1=4,
故选:C.
15.(2019?凉山州)如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=( )
A.1:2 B.1:3 C.1:4 D.2:3
【解答】解:如图,过O作OG∥BC,交AC于G,
法一:∵O是BD的中点,
∴G是DC的中点.
又AD:DC=1:2,
∴AD=DG=GC,
∴AG:GC=2:1,AO:OE=2:1,
∴S△AOB:S△BOE=2
设S△BOE=S,S△AOB=2S,又BO=OD,
∴S△AOD=2S,S△ABD=4S,
∵AD:DC=1:2,
∴S△BDC=2S△ABD=8S,S四边形CDOE=7S,
∴S△AEC=9S,S△ABE=3S,
∴
法二:∵OG∥BC,O为BD中点,
∴DG=CG,,
又∵AD:DC=1:2,
∴,
∴BE:EC=1:3.
故选:B.
二.填空题(共8小题)
16.(2020?庐阳区校级一模)已知,则的值为 .
【解答】解:∵,
∴7a﹣7b=3b,
则7a=10b,
则=.
故答案为:.
17.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 3.6 .
【解答】解:∵a∥b∥c,
∴=,
即=,
∴DE=3.6,
故答案为:3.6.
18.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= 6 .
【解答】解:∵a∥b∥c,
∴=,
∵AB=2,CB=4,DE=3,
∴=,
解得:EF=6,
故答案为:6.
19.(2019秋?海陵区期末)如图,E是?ABCD的BC边的中点,BD与AE相交于F,则△ABF与四边形ECDF的面积之比等于 .
【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵E是?ABCD的BC边的中点,
∴====,
∵△ABE和△ABF同高,
∴==,
∴S△ABE=S△ABF,
设?ABCD中,BC边上的高为h,
∵S△ABE=×BE×h,S?ABCD=BC×h=2×BE×h,
∴S?ABCD=4S△ABE=4×S△ABF=6S△ABF,
∵△ABF与△ADF等高,
∴==2,
∴S△ADF=2S△ABF,
∴S四边形ECDF=S?ABCD﹣S△ABE﹣S△ADF=S△ABF,
∴=,
故答案为:.
20.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【解答】解:如图,过点D作DF∥AE,
则==,
∵=,
∴DF=2EC,
∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
21.(2018秋?灌云县期末)电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB长为20米,主持人现站在A处,请问主持人应走到离A点至少多少米处才最自然得体?(结果精确到0.1米) 7.6米 .
【解答】解:根据黄金比得:20×(1﹣0.618)≈7.6米,
∵黄金分割点有2个,
∴20﹣7.6=12.4,
由于7.6<12.4米
∴主持人应走到离A点至少7.6米处才最自然得体.
故答案为:7.6米.
22.(2018秋?姜堰区校级月考)从美学角度来说,人的上身长与下身长之比为黄金比时,可以给人一种协调的美感.某女老师上身长约61.8cm,下身长约94cm,她要穿约 6 cm的高跟鞋才能达到黄金比的美感效果(精确到1cm).
【解答】解:设她要穿xcm的高跟鞋,
由题意得,=0.618,
解得x=6,
故答案为:6.
23.(2019?诸暨市模拟)如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若AB=,则MN= ﹣2 .
【解答】解:设MN=x.由题意可知DE=AB=,
∵∠EDM=∠ECD=36°,∠END=∠EDN=72°,
∴DE=EN,同理CD=CM,
∴EM=﹣x,EC=EN+CM﹣MN=﹣1﹣x,
∵∠DEM=∠DEC,
∴△DEM∽△CED,
∴DE2=EM?EC,
∴()2=(﹣x)(﹣1﹣x),
整理得x2﹣(﹣1)x+=0,
∴[x﹣(﹣1)]2=(﹣1)2,
∴x=﹣2或(﹣1)不合题意舍弃,
∴MN=﹣2.
故答案为:﹣2.
三.解答题(共9小题)
24.(2018秋?霍邱县期末)已知a:b:c=2:3:4,且2a+3b﹣2c=15,求a,b,c的值.
【解答】解:设a=2k,b=3k,c=4k,
∵2a+3b﹣2c=15,
∴4k+9k﹣8k=15,
解得k=3,
∴a=6,b=9,c=12.
25.(2019秋?昭平县期中)已知:线段a、b、c,且==.
(1)求的值.
(2)如线段a、b、c满足a+b+c=27,求a﹣b+c的值.
【解答】解:(1)∵=,
∴=,
∴=;
(2)设===k,则a=2k,b=3k,c=4k,
∵a+b+c=27,
∴2k+3k+4k=27,
∴k=3,
∴a=6,b=9,c=12,
∴a﹣b+c=6﹣9+12=9.
26.(2019?思明区校级模拟)如图,点C将线段AB分成两部分,若AC2=BC?AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
【解答】解:(Ⅰ)∵黄金抛物线的对称轴是直线x=2,
∴﹣=2,
∴b=﹣4a,又b2=ac
∴16a2=ac.
且与y轴交于点(0,8),
∴c=8.
∴a=,b=﹣2.
∴y=x2﹣2x+8
=(x﹣2)2+6,
∵>0,
∴y有最小值为6.
答:y的最小值为6.
(Ⅱ)原点是线段AB的黄金分割点.理由如下:
∵黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),
把它向下平移后与x轴交于A(+3,0),B(x0,0),
∴x0=﹣1﹣.
∴OA=3+,OB=1+,AB=4+2.
OA2=(3+)2=14+6.
OB?AB=(1+ )(4+2)=14+6.
∴OA2=OB?AB.
答:原点是线段AB的黄金分割点.
27.(2017秋?霍邱县期末)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC?CD的大小关系;
(2)求证:△ABC∽△BDC.
【解答】(1)解:AD2=AC?CD,理由如下:
∵AB=AC=1,AD=BC=,
∴CD=AC﹣AD
=1﹣
=,
∵AD2=()2=,AC?CD=,
∴AD2=AC?CD;
(2)由(1)知AD2=AC?CD,
∵AD=BC,
∴BC2=AC?CD,
∴=,
又∵∠C=∠C,
∴△ABC∽△BDC.
28.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
【解答】解:(1)∵l1∥l2∥l3,
∴,
即,
解得:AC=12;
(2)∵l1∥l2∥l3,
∴,
∵AB=4,AC=12,
∴BC=8,
∴OB=2,
∴.
29.(2019秋?长安区校级月考)如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
【解答】解:在△ABC中,因为EF∥AB,
所以EF:AB=CF:CB①,
同样,在△DBC中有EF:CD=BF:CB②,
①+②得EF:AB+EF:CD=CF:CB+BF:CB=1③.
设EF=x厘米,又已知AB=6厘米,CD=9厘米,代入③得
x:6+x:9=1,
解得x=.
故EF=厘米.
30.(2018秋?虹口区期中)如图,已知AD∥BE∥CF,它们依次交直线l1,l2于点A、B、C和点D、E、F,=,AC=10.
(1)求AB,BC的长;
(2)如果AD=7,CF=12,求BE的长.
【解答】解:(1)∵AD∥BE∥CF,
∴==,
∴=,
∵AC=10,
∴AB=4,
∴BC=10﹣4=6;
(2)如图所示:过点A作AG∥DF交BE于点H,交CF于点G,
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=12,
∴CG=12﹣7=5,
∵BE∥CF,
∴=,
∴BH=2,
∴BE=2+7=9.
31.(2018秋?长春期中)探究:如图①,在△ABC中,点D是BC的中点,点E在AB上,且=.过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,求的值.
应用:如图②,在△ABC中,点D是BC上的点=,点E在AB上,且=,过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,则= .
【解答】探究:解:∵DG∥BF,BD=CD,
∴CG=FG,
∴DG=BF,
∵BF∥AG,
∴==2,
∴AG=2BF,
∴==.
应用:解:∵DG∥BF,
∴==,
∴DG=
∵BF∥AG,
∴==2,
∴AG=2BF,
∴==,
故答案为.
_21?????????è?????(www.21cnjy.com)_
4.1比例线段黄金分割+4.2平行线分线段成比例练习(含解析)
一.选择题(共15小题)
1.(2019秋?越秀区期末)已知a=2b,那么下列等式中不一定成立的是( )
A.a+b=3b B.a﹣c=2b﹣c C.a=b D.=2
2.(2020春?万州区期末)若==,则的值是( )
A. B.﹣ C.﹣16 D.﹣
3.(2020春?芝罘区期中)在比例尺是1:200000的地图上,A、B两地间的距离为4cm,则A、B两地的实际距离是( )
A.8km B.5km C.80km D.0.5km
4.(2020?临潭县校级模拟)下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
5.(2020春?常熟市期末)点B是线段AC的黄金分割点,且AB<BC,若AC=2,则BC的长为( )
A. B. C.+1 D.﹣1
6.(2019秋?沙坪坝区校级期末)黄金分割数是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算2(﹣1)的值( )
A.在1和2之间 B.在2和3之间 C.在3和4之间 D.在4和5之间
7.(2020?金昌)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
8.(2019秋?杨浦区校级月考)直线DE交△ABC中的AB于D点,交AC于E点,那么能推出DE∥BC的条件是( )
A. B.
C. D.
9.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
10.(2020春?芝罘区期中)已知a,b,c是非零实数,且,求k的值为( )
A. B. C.﹣1或 D.﹣1或
11.(2019秋?抚州期末)如图,舞台纵深为6米,要想获得最佳音响效果,主持人应站在舞台纵深所在线段的离舞台前沿较近的黄金分割点P处,那么主持人站立的位置离舞台前沿较近的距离约为( )
A.1.1米 B.1.5米 C.1.9米 D.2.3米
12.如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
13.(2020?余杭区一模)如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E,则( )
A.= B.= C.= D.=
14.(2019春?朝阳区校级月考)如图,直线L1∥L2∥L3,直线L1、L2、L3分别和直线m交于点A、B、C,和直线n交于点A1、B1、C1.若AB=6,AC=9,A1B1=8,则线段B1C1的长为( )
A.2 B.3 C.4 D.5
15.(2019?凉山州)如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=( )
A.1:2 B.1:3 C.1:4 D.2:3
二.填空题(共8小题)
16.(2020?庐阳区校级一模)已知,则的值为 .
17.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 .
18.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= .
19.(2019秋?海陵区期末)如图,E是?ABCD的BC边的中点,BD与AE相交于F,则△ABF与四边形ECDF的面积之比等于 .
20.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
21.(2018秋?灌云县期末)电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB长为20米,主持人现站在A处,请问主持人应走到离A点至少多少米处才最自然得体?(结果精确到0.1米) .
22.(2018秋?姜堰区校级月考)从美学角度来说,人的上身长与下身长之比为黄金比时,可以给人一种协调的美感.某女老师上身长约61.8cm,下身长约94cm,她要穿约 cm的高跟鞋才能达到黄金比的美感效果(精确到1cm).
23.(2019?诸暨市模拟)如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若AB=,则MN= .
三.解答题(共9小题)
24.(2018秋?霍邱县期末)已知a:b:c=2:3:4,且2a+3b﹣2c=15,求a,b,c的值.
25.(2019秋?昭平县期中)已知:线段a、b、c,且==.
(1)求的值.
(2)如线段a、b、c满足a+b+c=27,求a﹣b+c的值.
26.(2019?思明区校级模拟)如图,点C将线段AB分成两部分,若AC2=BC?AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
27.(2017秋?霍邱县期末)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC?CD的大小关系;
(2)求证:△ABC∽△BDC.
28.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
29.(2019秋?长安区校级月考)如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
30.(2018秋?虹口区期中)如图,已知AD∥BE∥CF,它们依次交直线l1,l2于点A、B、C和点D、E、F,=,AC=10.
(1)求AB,BC的长;
(2)如果AD=7,CF=12,求BE的长.
31.(2018秋?长春期中)探究:如图①,在△ABC中,点D是BC的中点,点E在AB上,且=.过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,求的值.
应用:如图②,在△ABC中,点D是BC上的点=,点E在AB上,且=,过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,则= .
4.14.2参考答案与试题解析
一.选择题(共15小题)
1.(2019秋?越秀区期末)已知a=2b,那么下列等式中不一定成立的是( )
A.a+b=3b B.a﹣c=2b﹣c C.a=b D.=2
【解答】解:A、∵a=2b,∴a+b=3b,成立,不合题意;
B、∵a=2b,∴a﹣c=2b﹣c,成立,不合题意;
C、∵a=2b,∴a=b,成立,不合题意;
D、∵a=2b,∴=2(b≠0),原式不一定成立,符合题意.
故选:D.
2.(2020春?万州区期末)若==,则的值是( )
A. B.﹣ C.﹣16 D.﹣
【解答】解:∵==,
∴设a=2x,则b=3x,c=4x,
故原式=
=
=﹣.
故选:B.
3.(2020春?芝罘区期中)在比例尺是1:200000的地图上,A、B两地间的距离为4cm,则A、B两地的实际距离是( )
A.8km B.5km C.80km D.0.5km
【解答】解:设A、B两地的实际距离为xcm,
∵比例尺为1:200000,
∴4:x=1:200000,
∴x=800000,
800000cm=8km.
故选:A.
4.(2020?临潭县校级模拟)下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
【解答】解:A、∵2×5≠3×4,∴选项A不成比例;
B、∵2×8≠4×6,∴选项B不成比例;
C、∵3×12≠6×8,∴选项C不成比例;
D、∵1×15=3×5,∴选项D成比例.
故选:D.
5.(2020春?常熟市期末)点B是线段AC的黄金分割点,且AB<BC,若AC=2,则BC的长为( )
A. B. C.+1 D.﹣1
【解答】解:∵点B是线段AC的黄金分割点,且AB<BC,
∴BC=AC,
∵AC=2,
∴BC=﹣1.
故选:D.
6.(2019秋?沙坪坝区校级期末)黄金分割数是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算2(﹣1)的值( )
A.在1和2之间 B.在2和3之间 C.在3和4之间 D.在4和5之间
【解答】解:∵<,
又∵2(﹣1)=2﹣2,
∴4<2<5,
∴2<2﹣2<3,
∴2(﹣1)的值在2和3之间;
故选:B.
7.(2020?金昌)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
【解答】解:∵雕像的腰部以下a与全身b的高度比值接近0.618,
∴≈0.618,
∵b为2米,
∴a约为1.24米.
故选:A.
8.(2019秋?杨浦区校级月考)直线DE交△ABC中的AB于D点,交AC于E点,那么能推出DE∥BC的条件是( )
A. B.
C. D.
【解答】解:A.由不能得到对应线段成比例,即不能推出DE∥BC,不合题意;
B.由可得到对应线段成比例,即可推出DE∥BC,符合题意;
C.由不能得到对应线段成比例,即不能推出DE∥BC,不合题意;
D.由不能得到对应线段成比例,即不能推出DE∥BC,不合题意;
故选:B.
9.(2020?雨花区校级一模)如图,直线a∥b∥c,则下列结论不正确的为( )
A. B. C. D.
【解答】解:A、∵a∥b∥c,
∴=,本选项结论正确,不符合题意;
B、∵a∥b∥c,
∴=,本选项结论正确,不符合题意;
C、∵a∥b∥c,
∴=,本选项结论正确,不符合题意;
D、连接AF,交BE于H,
∵b∥c,
∴△ABH∽△ACF,
∴=≠,本选项结论不正确,符合题意;
故选:D.
10.(2020春?芝罘区期中)已知a,b,c是非零实数,且,求k的值为( )
A. B. C.﹣1或 D.﹣1或
【解答】解:∵,
∴a=(b+c)k,b=(a+c)k,c=(a+b)k,
∴a+b+c=2(a+b+c)k,
∴①当a+b+c≠0时,k=,
②当a+b+c=0时,a=﹣(b+c),
k==﹣1,
综上所述:k=﹣1或.
故选:D.
11.(2019秋?抚州期末)如图,舞台纵深为6米,要想获得最佳音响效果,主持人应站在舞台纵深所在线段的离舞台前沿较近的黄金分割点P处,那么主持人站立的位置离舞台前沿较近的距离约为( )
A.1.1米 B.1.5米 C.1.9米 D.2.3米
【解答】解:∵节目主持人应站在舞台的黄金分割处,
∴距前沿较近的距离 6×=9﹣3≈2.3(米),
故选:D.
12.如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
【解答】解:∵DE∥AB,
∴==,
∴的值为,
故选:A.
13.(2020?余杭区一模)如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E,则( )
A.= B.= C.= D.=
【解答】解:∵ME∥CD,
∴=,
∴=.
故选:D.
14.(2019春?朝阳区校级月考)如图,直线L1∥L2∥L3,直线L1、L2、L3分别和直线m交于点A、B、C,和直线n交于点A1、B1、C1.若AB=6,AC=9,A1B1=8,则线段B1C1的长为( )
A.2 B.3 C.4 D.5
【解答】解:∵直线L1∥L2∥L3,
∴=,
∵AB=6,AC=9,
∴BC=3,
∴=,
∴B1C1=4,
故选:C.
15.(2019?凉山州)如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=( )
A.1:2 B.1:3 C.1:4 D.2:3
【解答】解:如图,过O作OG∥BC,交AC于G,
法一:∵O是BD的中点,
∴G是DC的中点.
又AD:DC=1:2,
∴AD=DG=GC,
∴AG:GC=2:1,AO:OE=2:1,
∴S△AOB:S△BOE=2
设S△BOE=S,S△AOB=2S,又BO=OD,
∴S△AOD=2S,S△ABD=4S,
∵AD:DC=1:2,
∴S△BDC=2S△ABD=8S,S四边形CDOE=7S,
∴S△AEC=9S,S△ABE=3S,
∴
法二:∵OG∥BC,O为BD中点,
∴DG=CG,,
又∵AD:DC=1:2,
∴,
∴BE:EC=1:3.
故选:B.
二.填空题(共8小题)
16.(2020?庐阳区校级一模)已知,则的值为 .
【解答】解:∵,
∴7a﹣7b=3b,
则7a=10b,
则=.
故答案为:.
17.(2020?淮安区一模)如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=3,BC=4,EF=4.8,则DE的长为 3.6 .
【解答】解:∵a∥b∥c,
∴=,
即=,
∴DE=3.6,
故答案为:3.6.
18.(2020春?吴中区期末)如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF= 6 .
【解答】解:∵a∥b∥c,
∴=,
∵AB=2,CB=4,DE=3,
∴=,
解得:EF=6,
故答案为:6.
19.(2019秋?海陵区期末)如图,E是?ABCD的BC边的中点,BD与AE相交于F,则△ABF与四边形ECDF的面积之比等于 .
【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵E是?ABCD的BC边的中点,
∴====,
∵△ABE和△ABF同高,
∴==,
∴S△ABE=S△ABF,
设?ABCD中,BC边上的高为h,
∵S△ABE=×BE×h,S?ABCD=BC×h=2×BE×h,
∴S?ABCD=4S△ABE=4×S△ABF=6S△ABF,
∵△ABF与△ADF等高,
∴==2,
∴S△ADF=2S△ABF,
∴S四边形ECDF=S?ABCD﹣S△ABE﹣S△ADF=S△ABF,
∴=,
故答案为:.
20.(2020?无锡)如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【解答】解:如图,过点D作DF∥AE,
则==,
∵=,
∴DF=2EC,
∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
21.(2018秋?灌云县期末)电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图,若舞台AB长为20米,主持人现站在A处,请问主持人应走到离A点至少多少米处才最自然得体?(结果精确到0.1米) 7.6米 .
【解答】解:根据黄金比得:20×(1﹣0.618)≈7.6米,
∵黄金分割点有2个,
∴20﹣7.6=12.4,
由于7.6<12.4米
∴主持人应走到离A点至少7.6米处才最自然得体.
故答案为:7.6米.
22.(2018秋?姜堰区校级月考)从美学角度来说,人的上身长与下身长之比为黄金比时,可以给人一种协调的美感.某女老师上身长约61.8cm,下身长约94cm,她要穿约 6 cm的高跟鞋才能达到黄金比的美感效果(精确到1cm).
【解答】解:设她要穿xcm的高跟鞋,
由题意得,=0.618,
解得x=6,
故答案为:6.
23.(2019?诸暨市模拟)如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若AB=,则MN= ﹣2 .
【解答】解:设MN=x.由题意可知DE=AB=,
∵∠EDM=∠ECD=36°,∠END=∠EDN=72°,
∴DE=EN,同理CD=CM,
∴EM=﹣x,EC=EN+CM﹣MN=﹣1﹣x,
∵∠DEM=∠DEC,
∴△DEM∽△CED,
∴DE2=EM?EC,
∴()2=(﹣x)(﹣1﹣x),
整理得x2﹣(﹣1)x+=0,
∴[x﹣(﹣1)]2=(﹣1)2,
∴x=﹣2或(﹣1)不合题意舍弃,
∴MN=﹣2.
故答案为:﹣2.
三.解答题(共9小题)
24.(2018秋?霍邱县期末)已知a:b:c=2:3:4,且2a+3b﹣2c=15,求a,b,c的值.
【解答】解:设a=2k,b=3k,c=4k,
∵2a+3b﹣2c=15,
∴4k+9k﹣8k=15,
解得k=3,
∴a=6,b=9,c=12.
25.(2019秋?昭平县期中)已知:线段a、b、c,且==.
(1)求的值.
(2)如线段a、b、c满足a+b+c=27,求a﹣b+c的值.
【解答】解:(1)∵=,
∴=,
∴=;
(2)设===k,则a=2k,b=3k,c=4k,
∵a+b+c=27,
∴2k+3k+4k=27,
∴k=3,
∴a=6,b=9,c=12,
∴a﹣b+c=6﹣9+12=9.
26.(2019?思明区校级模拟)如图,点C将线段AB分成两部分,若AC2=BC?AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
【解答】解:(Ⅰ)∵黄金抛物线的对称轴是直线x=2,
∴﹣=2,
∴b=﹣4a,又b2=ac
∴16a2=ac.
且与y轴交于点(0,8),
∴c=8.
∴a=,b=﹣2.
∴y=x2﹣2x+8
=(x﹣2)2+6,
∵>0,
∴y有最小值为6.
答:y的最小值为6.
(Ⅱ)原点是线段AB的黄金分割点.理由如下:
∵黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),
把它向下平移后与x轴交于A(+3,0),B(x0,0),
∴x0=﹣1﹣.
∴OA=3+,OB=1+,AB=4+2.
OA2=(3+)2=14+6.
OB?AB=(1+ )(4+2)=14+6.
∴OA2=OB?AB.
答:原点是线段AB的黄金分割点.
27.(2017秋?霍邱县期末)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC?CD的大小关系;
(2)求证:△ABC∽△BDC.
【解答】(1)解:AD2=AC?CD,理由如下:
∵AB=AC=1,AD=BC=,
∴CD=AC﹣AD
=1﹣
=,
∵AD2=()2=,AC?CD=,
∴AD2=AC?CD;
(2)由(1)知AD2=AC?CD,
∵AD=BC,
∴BC2=AC?CD,
∴=,
又∵∠C=∠C,
∴△ABC∽△BDC.
28.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
【解答】解:(1)∵l1∥l2∥l3,
∴,
即,
解得:AC=12;
(2)∵l1∥l2∥l3,
∴,
∵AB=4,AC=12,
∴BC=8,
∴OB=2,
∴.
29.(2019秋?长安区校级月考)如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
【解答】解:在△ABC中,因为EF∥AB,
所以EF:AB=CF:CB①,
同样,在△DBC中有EF:CD=BF:CB②,
①+②得EF:AB+EF:CD=CF:CB+BF:CB=1③.
设EF=x厘米,又已知AB=6厘米,CD=9厘米,代入③得
x:6+x:9=1,
解得x=.
故EF=厘米.
30.(2018秋?虹口区期中)如图,已知AD∥BE∥CF,它们依次交直线l1,l2于点A、B、C和点D、E、F,=,AC=10.
(1)求AB,BC的长;
(2)如果AD=7,CF=12,求BE的长.
【解答】解:(1)∵AD∥BE∥CF,
∴==,
∴=,
∵AC=10,
∴AB=4,
∴BC=10﹣4=6;
(2)如图所示:过点A作AG∥DF交BE于点H,交CF于点G,
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=12,
∴CG=12﹣7=5,
∵BE∥CF,
∴=,
∴BH=2,
∴BE=2+7=9.
31.(2018秋?长春期中)探究:如图①,在△ABC中,点D是BC的中点,点E在AB上,且=.过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,求的值.
应用:如图②,在△ABC中,点D是BC上的点=,点E在AB上,且=,过点B作AD的平行线与CE的延长线交于点F,CF与AD交于点G,则= .
【解答】探究:解:∵DG∥BF,BD=CD,
∴CG=FG,
∴DG=BF,
∵BF∥AG,
∴==2,
∴AG=2BF,
∴==.
应用:解:∵DG∥BF,
∴==,
∴DG=
∵BF∥AG,
∴==2,
∴AG=2BF,
∴==,
故答案为.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
