1.4 二次函数的综合运用培优精选试题(面积、动点、利润、最值、存在性)(含解析)
文档属性
| 名称 | 1.4 二次函数的综合运用培优精选试题(面积、动点、利润、最值、存在性)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-16 10:36:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级(上)二次函数的运用
一、解答题(共30小题)
1.(2020?攀枝花)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
2.(2020?宜兴市一模)在平面直角坐标系中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且S△ABC:S△BCE=3:4.
(1)求点A,点B的坐标;
(2)将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
①求直线CE的解析式;
②求抛物线的解析式.
3.(2020?沭阳县模拟)“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降2元,则每月可多销售10条,设每条裤子的售价为x元(x为正整数),每月的销售量为y条.
(1)直接写出y与x的函数关系式;
(2)设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润不低于4175元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
4.(2020?溧阳市模拟)如图,已知二次函数y=x2+bx的图象经过点A(﹣4,0),顶点为B,一次函数y=x+2的图象交y轴于点M,P是抛物线上一点,点M关于直线AP的对称点N恰好落在抛物线的对称轴直线BH上(对称轴直线BH与x轴交于点H).
(1)求二次函数的表达式;
(2)求点P的坐标;
(3)若点G是第二象限内抛物线上一点,G关于抛物线的对称轴的对称点是E,连接OG,点F是线段OG上一点,点D是坐标平面内一点,若四边形BDEF是正方形,求点G的坐标.
5.(2020?孝南区二模)已知抛物线y=ax2+bx﹣6与x轴交于A(﹣2,0),B(3,0)两点,与y轴交于点C,连结BC.
(1)填空:a= ,b= ;
(2)如图1,若D为抛物线上BC下方一动点(不与C,B重合),连OD交BC于E,求的最大值;
(3)如图2,点P在抛物线上,且∠BCO=∠PBA,请直接写出P点的坐标.
6.(2020?沭阳县模拟)如图1,在平面直角坐标系中,已知点A的坐标是(3,0),并且OA=OC=3OB,动点P在过A,B,C三点的抛物线上,
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为底的等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,以线段EF的中点G为圆心,以EF为直径作⊙G,求⊙G最小面积.
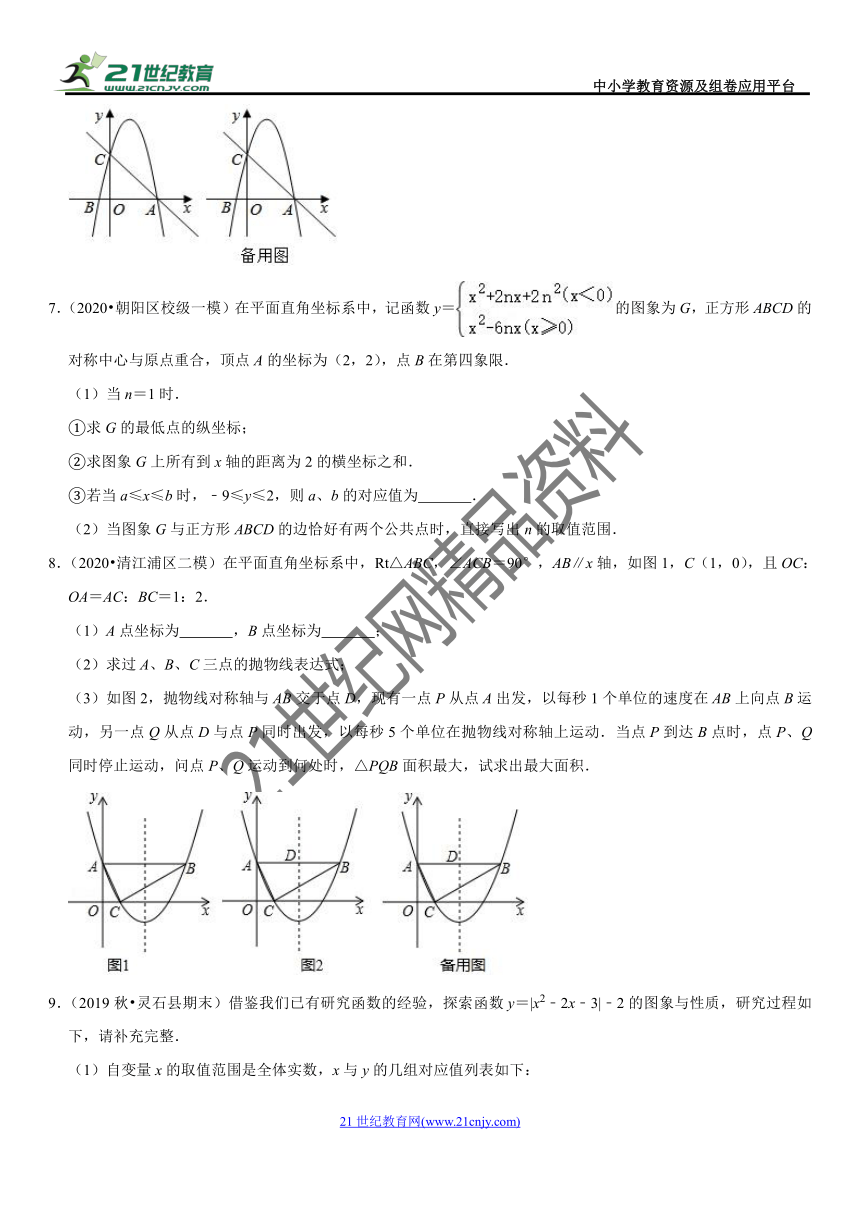
7.(2020?朝阳区校级一模)在平面直角坐标系中,记函数y=的图象为G,正方形ABCD的对称中心与原点重合,顶点A的坐标为(2,2),点B在第四象限.
(1)当n=1时.
①求G的最低点的纵坐标;
②求图象G上所有到x轴的距离为2的横坐标之和.
③若当a≤x≤b时,﹣9≤y≤2,则a、b的对应值为 .
(2)当图象G与正方形ABCD的边恰好有两个公共点时,直接写出n的取值范围.
8.(2020?清江浦区二模)在平面直角坐标系中,Rt△ABC,∠ACB=90°,AB∥x轴,如图1,C(1,0),且OC:OA=AC:BC=1:2.
(1)A点坐标为 ,B点坐标为 ;
(2)求过A、B、C三点的抛物线表达式;
(3)如图2,抛物线对称轴与AB交于点D,现有一点P从点A出发,以每秒1个单位的速度在AB上向点B运动,另一点Q从点D与点P同时出发,以每秒5个单位在抛物线对称轴上运动.当点P到达B点时,点P、Q同时停止运动,问点P、Q运动到何处时,△PQB面积最大,试求出最大面积.
9.(2019秋?灵石县期末)借鉴我们已有研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象与性质,研究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 …
y … 10 m ﹣2 1 n 1 ﹣2 3 10 …
其中,m= ,n= ;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①写出函数的一条图象性质: ;
②当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根,根据函数图象直接写出的取值范围为 .
10.(2020春?南岸区校级月考)如图,抛物线y=x2+2x﹣3与x轴交于A、B两点(点A在点B的左侧),交y轴于点C,抛物线的顶点为点D.
(1)求AB的长度和点D的坐标;
(2)求直线AC的函数表达式;
(3)点P是第四象限抛物线上一点,当2S△PAC=S△PAB时,求点P的坐标.
11.(2020?雁塔区校级模拟)如图,直线y=﹣x﹣3与坐标轴交于点A、C,经过点A、C的抛物线.y=ax2+bx+c与x轴交于点B(2,0),点D是抛物线在第三象限图象上的动点,过点D作DE⊥x轴于点E,交AC于点F.
(1)求该二次函数的解析式;
(2)若线段AC恰好将△ADE的面积分成1:4的两部分,请求出此时点D的坐标.
12.(2020?东营)如图,抛物线y=ax2﹣3ax﹣4a的图象经过点C(0,2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的解析式及点A、B的坐标;
(2)是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
13.(2020?宿迁)某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价x(元/千克) 55 60 65 70
销售量y(千克) 70 60 50 40
(1)求y(千克)与x(元/千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
14.(2020?随州)2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格p(元/只)和销量q(只)与第x天的关系如下表:
第x天 1 2 3 4 5
销售价格p(元/只) 2 3 4 5 6
销量q(只) 70 75 80 85 90
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元/只,该药店从第6天起将该型号口罩的价格调整为1元/只.据统计,该药店从第6天起销量q(只)与第x天的关系为q=﹣2x2+80x﹣200 (6≤x≤30,且x为整数),已知该型号口罩的进货价格为0.5元/只.
(1)直接写出该药店该月前5天的销售价格p与x和销量q与x之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润W(元)与x的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m倍的罚款,若罚款金额不低于2000元,则m的取值范围为 .
15.(2020?荆门)2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为p=,销售量y(千克)与x之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
16.(2019秋?宁明县期中)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.求S与x之间的函数表达式,并求自变量x的取值范围.
17.(2020?湖州模拟)如图,已知在平面直角坐标系xOy中,直线y=x+b经过点B(1,3),且与直线y=﹣2x交于点A,抛物线y=(x﹣m)2+n的顶点在直线y=﹣2x上运动.
(1)求点A的坐标.
(2)当抛物线经过点A时,求抛物线的解析式.
(3)当﹣1<x<1时,始终满足(x﹣m)2+n<x+b,结合图象,直接写出m的取值范围.
18.(2020?宁波模拟)如图,抛物线y1=﹣x2﹣x+c与直线y2=x+b交于A,B(1,0)两点.
(1)分别求c,b的值.
(2)求y1﹣y2的最大值.
(3)求点A的坐标,并根据图象判断,当x取何值时,y1>y2?
19.(2020?镇海区模拟)如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
20.(2020?雅安)已知二次函数y=x2+bx+c(a≠0)的图象与x轴的交于A、B(1,0)两点,与y轴交于点C(0,﹣3),
(1)求二次函数的表达式及A点坐标;
(2)D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标;
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以M、N、B、O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
21.(2020?丹东)如图1,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,A点坐标为(﹣2,0),与y轴交于点C(0,4),直线y=﹣x+m与抛物线交于B,D两点.
(1)求抛物线的函数表达式.
(2)求m的值和D点坐标.
(3)点P是直线BD上方抛物线上的动点,过点P作x轴的垂线,垂足为H,交直线BD于点F,过点D作x轴的平行线,交PH于点N,当N是线段PF的三等分点时,求P点坐标.
(4)如图2,Q是x轴上一点,其坐标为(﹣,0).动点M从A出发,沿x轴正方向以每秒5个单位的速度运动,设M的运动时间为t(t>0),连接AD,过M作MG⊥AD于点G,以MG所在直线为对称轴,线段AQ经轴对称变换后的图形为A′Q′,点M在运动过程中,线段A′Q′的位置也随之变化,请直接写出运动过程中线段A′Q′与抛物线有公共点时t的取值范围.
22.(2020?永州)在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,且AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知Q(1,﹣)是抛物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.
23.(2020?鄂尔多斯)如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数解析式;
(2)点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;
(3)如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.
24.(2020?鄂州)如图,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C.直线y=x﹣2经过B、C两点.
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线BC及x轴分别交于点D、M.PN⊥BC,垂足为N.设M(m,0).
①点P在抛物线上运动,若P、D、M三点中恰有一点是其它两点所连线段的中点(三点重合除外).请直接写出符合条件的m的值;
②当点P在直线BC下方的抛物线上运动时,是否存在一点P,使△PNC与△AOC相似.若存在,求出点P的坐标;若不存在,请说明理由.
25.(2020?恩施州)如图1,抛物线y=﹣x2+bx+c经过点C(6,0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点.
(1)求抛物线的解析式;
(2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90°,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=﹣x2+bx+c只有一个交点时,求点M的坐标.
(3)△MPC在(2)的旋转变换下,若PC=(如图2).
①求证:EA=ED.
②当点E在(1)所求的抛物线上时,求线段CM的长.
26.(2020?青海)如图1(注:与图2完全相同)所示,抛物线y=﹣+bx+c经过B、D两点,与x轴的另一个交点为A,与y轴相交于点C.
(1)求抛物线的解析式.
(2)设抛物线的顶点为M,求四边形ABMC的面积.(请在图1中探索)
(3)设点Q在y轴上,点P在抛物线上.要使以点A、B、P、Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)
27.(2020?山西)综合与探究
如图,抛物线y=x2﹣x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为(4,﹣3).
(1)请直接写出A,B两点的坐标及直线l的函数表达式;
(2)若点P是抛物线上的点,点P的横坐标为m(m≥0),过点P作PM⊥x轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标;
(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.
28.(2020?淄博)如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx+(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是?OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
29.(2020?青岛)某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
(1)按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k≠0)表示.求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2.已知GM=2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)
(3)根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
30.(2020?咸宁)如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n<)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
二次函数的运用
参考答案与试题解析
一.选择题
二.解答题(共31小题)
1.(2020?攀枝花)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
【解答】解:(1)∵A(﹣1,0),B(2,0),C(0,4),
设抛物线表达式为:y=a(x+1)(x﹣2),
将C代入得:4=﹣2a,
解得:a=﹣2,
∴该抛物线的解析式为:y=﹣2(x+1)(x﹣2)=﹣2x2+2x+4;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,
∵A(﹣1,0),B(2,0),C(0,4),
可得:OA=1,OC=4,OB=2,
∴S=S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(﹣2m2+2m+4)
=﹣2m2+4m+6
=﹣2(m﹣1)2+8,
当m=1时,S最大,最大值为8.
2.(2020?宜兴市一模)在平面直角坐标系中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且S△ABC:S△BCE=3:4.
(1)求点A,点B的坐标;
(2)将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
①求直线CE的解析式;
②求抛物线的解析式.
【解答】解:(1)如图,过点C作CF⊥AB于F,
∵抛物线y=mx2﹣4mx+n(m>0),
∴对称轴为直线x=2,
∴AF=BF,点F(2,0),即OF=2,
∵S△ABC:S△BCE=3:4,
∴S△ABC=3S△ABE,
∴3××AB×OE=AB×CF,
∴CF=3OE,
∵CF⊥AB,OE⊥AB,
∴CF∥OE,
∴,
∴AF=3OA,
∵OF=OA+AF=2,
∴OA=,AF=,
∴点A坐标为(,0),
∵AB=2AF=3,
∴OB=,
∴点B坐标为(,0);
(2)①∵抛物线y=mx2﹣4mx+n(m>0)过点A(,0),
∴0=m﹣2m+n,
∴n=m,
∴y=mx2﹣4mx+n=m(x﹣2)2﹣m,
∴点C(2,﹣m),
如图2,过点C作CF⊥OB于F,CH⊥y轴于H,
又∵∠FOH=90°,
∴四边形OFCH是矩形,
∴CF=OH=m,
∵将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
∴OC=O'C,OB=O'A=,
又∵CH⊥OO',
∴OO'=2OH=m,
∵OA2+O'O2=O'A2,
∴+m2=,
∴m=,
∴点C坐标为(2,﹣),
设直线CE的解析式为y=kx+b,
∴,
解得:
∴直线CE的解析式为y=﹣x+;
②∵m=,
∴y=x2﹣x+.
3.(2020?沭阳县模拟)“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降2元,则每月可多销售10条,设每条裤子的售价为x元(x为正整数),每月的销售量为y条.
(1)直接写出y与x的函数关系式;
(2)设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润不低于4175元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
【解答】解:(1)由题意可得:
y=100+×10
=100+5(80﹣x)
=﹣5x+500,
∴y与x的函数关系式为:y=﹣5x+500;
(2)由题意得:
w=(x﹣40)(﹣5x+500)
=﹣5x2+700x﹣20000
=﹣5(x﹣70)2+4500,
∵a=﹣5<0,
∴当x=70时,w有最大利润,最大利润是4500元;
∴应降价80﹣70=10(元).
∴当销售单价降低10元时,每月获得的利润最大,最大利润是4500元;
(3)由题意得:﹣5(x﹣70)2+4500=4175+200,
解得:x1=65,x2=75,
∵抛物线开口向下,对称轴为直线x=70,
∴当65≤x≤75时,符合该网店要求,
而为了让顾客得到最大实惠,故x=65.
∴当销售单价定为65元时,既符合网店要求,又能让顾客得到最大实惠.
4.(2020?溧阳市模拟)如图,已知二次函数y=x2+bx的图象经过点A(﹣4,0),顶点为B,一次函数y=x+2的图象交y轴于点M,P是抛物线上一点,点M关于直线AP的对称点N恰好落在抛物线的对称轴直线BH上(对称轴直线BH与x轴交于点H).
(1)求二次函数的表达式;
(2)求点P的坐标;
(3)若点G是第二象限内抛物线上一点,G关于抛物线的对称轴的对称点是E,连接OG,点F是线段OG上一点,点D是坐标平面内一点,若四边形BDEF是正方形,求点G的坐标.
【解答】解:(1)∵二次函数y=x2+bx的图象经过点A(﹣4,0),
∴0=8﹣4b,
∴b=2,
∴二次函数的解析式为y=x2+2x.
(2)如图1中,当点P在第一象限时,
由题意A(﹣4,0),H(﹣2,0),M(0,2),
∵点M,K关于AP对称,
∴AK=AM==2,
∴KH==4,
∴K(﹣2,4),
∴直线MK的解析式为y=﹣x+2,
∵PA⊥MK,
∴直线PA的解析式为y=x+4,
由,解得或,
∴P(2,6).
如图2中,当点P在第三象限时,同法可得K(﹣2,﹣4),
∴直线MK的解析式为y=3x+2,
∵AP⊥MK,
∴直线AP的解析式为y=﹣x﹣,
由,解得或﹣,
∴P(﹣,﹣),
综上所述,满足条件的点P坐标为(2,6)或(﹣,﹣).
(3)如图3中,设G(m,m2+2m),过点F作FN⊥GE于N,过点F作FP⊥BH于P,设直线BH交GE于Q,设GE交y轴于K.
∵四边形EFBD是正方形,
∴EF=BF,∠EFB=90°,
∵∠ENF=∠FPB=90°,∠PNQ=∠FPQ=∠NQP=90°,
∴四边形PFNQ是矩形,
∴∠NFP=∠EFB,
∴∠EFN=∠BFP,
∴△ENF≌△BPF(AAS),
∴PF=FN,EN=BP,
∴四边形PFNQ是正方形,设PF=FN=NQ=PQ=a,
∵PN∥OK,
∴=,
∴=,
∴GN=﹣,
∵NE=PB,
∴﹣2﹣m+a=﹣4﹣m+=m2+2m﹣a,
解得m=﹣6或﹣4(舍弃),
∴G(﹣6,6).
5.(2020?孝南区二模)已知抛物线y=ax2+bx﹣6与x轴交于A(﹣2,0),B(3,0)两点,与y轴交于点C,连结BC.
(1)填空:a= 1 ,b= 1 ;
(2)如图1,若D为抛物线上BC下方一动点(不与C,B重合),连OD交BC于E,求的最大值;
(3)如图2,点P在抛物线上,且∠BCO=∠PBA,请直接写出P点的坐标.
【解答】解:(1)∵抛物线y=ax2+bx﹣6与x轴交于A(﹣2,0),B(3,0)两点,
∴,
解得,,
故答案为:1,﹣1;
(2)如图,过D点作DH⊥x轴,垂足为H,交BC于点F,
在y=x2﹣x﹣6中,当x=0时,y=﹣6,
∴C(0,﹣6),
设直线BC解析式为:y=kx+b,
把(3,0),(0,﹣6)代入得:
,解得,,
∴直线BC的解析式为y=2x﹣6,
设D(x,x2﹣x﹣6),F(x,2x﹣6),
∴OC=6,DF=2x﹣6﹣(x2﹣x﹣6)=﹣x2+3x,
又∵DH⊥x轴,
∴DH∥y轴,
∴△DEF∽△OEC,
∴,
设的比值为W,
则W===( x2 ﹣3x)=(x)2+,
∴当x=时,W有最大值,最大值为,
∴的最大值为;
(3)如图,作BC的垂直平分线交y轴于点D,连接BD,则有DC=DB,
∴∠DCB=∠DBC,
∴∠BDO=2∠BCO,
再在y轴正半轴上取一点E,使∠EBO=∠BDO,
∴∠EBO=2∠BCO,
又∵∠BCO=∠PBA,
∴直线BE与抛物线交于点P,
∵A(﹣2,0),B(3,0),C(0,﹣6),
∴OA=2,OB=3,OC=6,
设CD=BD=x,OD=6﹣x,
∴(6﹣x)2+32=x2
x=,
∴OD=,
又∵∠BOD=∠BOE=90°,
∴△BOD∽△EOB
∴,
∴,
∴OE=4,
①设直线BE解析式为y=kx+b,把(3,0),(0,4)代入得,
,解得,,
∴直线BE的解析式为 y=﹣+4,
∴,
解得,x1=,x2=3(舍去),
∴点P的坐标为(﹣,);
②若E点在y轴负半轴上,则坐标为(0,﹣4),直线BE解析式为y=x﹣4,
则可得方程组
,
解得:x3=﹣,x4=3(舍去),
∴点P的坐标为(﹣,﹣),
综上所述点P的坐标为(﹣,)或(﹣,﹣).
6.(2020?沭阳县模拟)如图1,在平面直角坐标系中,已知点A的坐标是(3,0),并且OA=OC=3OB,动点P在过A,B,C三点的抛物线上,
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为底的等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,以线段EF的中点G为圆心,以EF为直径作⊙G,求⊙G最小面积.
【解答】解:(1)∵点A的坐标是(3,0),
∴OA=3,
∵OA=OC=3OB,
∴OC=3,OB=1,
∴点C(0,3),点B(﹣1,0),
设抛物线的解析式为:y=a(x+1)(x﹣3),
∴3=﹣3a,
∴a=﹣1,
∴抛物线解析式为:y=﹣(x+1)(x﹣3)=﹣x2+2x+3;
(2)∵△ACP是以AC为底的等腰三角形,
∴AP=CP,
又∵OA=OC,
∴OP是AC的垂直平分线,
∵OA=OC,∠AOC=90°,OP是AC的垂直平分线,
∴OP平分∠AOC,
∴直线OP解析式为y=x,
联立方程组可得:,
∴或,
∴点P坐标为(,)或(,);
(3)如图,
∵点A的坐标是(3,0),点C坐标为(0,3),
∴直线AC解析式为:y=﹣x+3,
设点D坐标为(m,﹣m+3),
∴DE=|m|,DF=|﹣m+3|,
∴EF2=DE2+DF2=m2+(﹣m+3)2,
∵⊙G的面积=×EF2=×[m2+(﹣m+3)2]=×[2(m﹣)2+],
∴当m=时,⊙G最小面积为.
7.(2020?朝阳区校级一模)在平面直角坐标系中,记函数y=的图象为G,正方形ABCD的对称中心与原点重合,顶点A的坐标为(2,2),点B在第四象限.
(1)当n=1时.
①求G的最低点的纵坐标;
②求图象G上所有到x轴的距离为2的横坐标之和.
③若当a≤x≤b时,﹣9≤y≤2,则a、b的对应值为 a=﹣2,b=3或a=3,b=3+或a=﹣2,b=3+ .
(2)当图象G与正方形ABCD的边恰好有两个公共点时,直接写出n的取值范围.
【解答】解:(1)①y=,
函数图象如图所示:
函数最低点的坐标(3,﹣9),
∴图象G的最低点的纵坐标为﹣9.
②当y=2时,x2+2x+2=2,解得x=﹣2或0(舍弃)
x2﹣6x=2时,解得x=3+或3﹣(舍弃),
当y=﹣2时,x2﹣6x=﹣2,解得x=3+或3﹣,
∴图象G上所有到x轴的距离为2的横坐标之和=﹣2+3++3++3﹣=7+.
③观察图象可知:当﹣2≤x≤3或3≤x≤3+或﹣2≤x≤3+时,﹣9≤y≤2,
∴a=﹣2,b=3或a=3,b=3+或a=﹣2,b=3+.
故答案为:a=﹣2,b=3或a=3,b=3+或a=﹣2,b=3+.
(2)当y=x2+2nx+2n2的顶点落在AD边上时,n2=2,解得n=或﹣(舍弃)
当n=时,y=x2+2nx+2n2(x<0)与边AD有一个交点,y=x2﹣6nx与边BC有一个交点,符合题意.
当2n2≤2,解得n≤1或n≥﹣1,
当y=x2﹣6nx经过(2,﹣2)时,n=,
观察图象可知当<n≤1时,满足条件,
当y=x2﹣6nx的顶点在BC边上时,﹣9n2=﹣2,
解得n=或﹣(舍弃),
当n=﹣1时,y=x2+2nx+2n2(x<0)与正方形的边没有交点,
观察图象可知当﹣1<n<时,满足条件,
综上所述,满足条件的n的值为﹣1<n<或<n≤1或n=.
8.(2020?清江浦区二模)在平面直角坐标系中,Rt△ABC,∠ACB=90°,AB∥x轴,如图1,C(1,0),且OC:OA=AC:BC=1:2.
(1)A点坐标为 (0,2) ,B点坐标为 (5,2) ;
(2)求过A、B、C三点的抛物线表达式;
(3)如图2,抛物线对称轴与AB交于点D,现有一点P从点A出发,以每秒1个单位的速度在AB上向点B运动,另一点Q从点D与点P同时出发,以每秒5个单位在抛物线对称轴上运动.当点P到达B点时,点P、Q同时停止运动,问点P、Q运动到何处时,△PQB面积最大,试求出最大面积.
【解答】解:(1)∵C(1,0),
∴OC=1,
∵OC:OA=1:2,
∴OA=2,
∴A(0,2),
∴AC==,
∵AC:BC=1:2,
∴BC=2,
∵∠ACB=90°,
∴AB===5,
∵AB∥x轴,
∴B(5,2),
故答案为:(0,2),(5,2);
(2)设过A、B、C三点的抛物线表达式为:y=ax2+bx+c,
则,
解得:,
∴过A、B、C三点的抛物线表达式为:y=x2﹣x+2;
(3)如图2,设运动t秒时,△PQB面积最大,且0≤t≤5,则BP=5﹣t,DQ=5t,
∴S△PQB===﹣,
∵a=﹣<0
∴当t=﹣=时,面积最大值是:S△PQB=﹣=,
此时点P的坐标为(,2),
当点Q向上运动时,点Q的坐标为(,),
当点Q向下运动时,点Q的坐标为(,﹣),
综上,当点P的坐标为(,2),点Q的坐标为(,)或(,﹣)时,△PQB面积最大,最大面积为.
9.(2019秋?灵石县期末)借鉴我们已有研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象与性质,研究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 …
y … 10 m ﹣2 1 n 1 ﹣2 3 10 …
其中,m= 3 ,n= 2 ;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①写出函数的一条图象性质: 图象具有对称性,对称轴是直线x=1 ;
②当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根,根据函数图象直接写出的取值范围为 b=﹣2或b>2 .
【解答】解:(1)把x=﹣2代入y=|x2﹣2x﹣3|﹣2,得y=3,
∴m=3,
把x=1代入y=|x2﹣2x﹣3|﹣2,得y=2,
∴n=2,
故答案为:3,2;
(2)如图所示;
(3)①函数的性质:图象具有对称性,对称轴是直线x=1;
故答案为图象具有对称性,对称轴是直线x=1:
②由图象可知,当b=﹣2或b>2时,函数y=|x2﹣2x﹣3|﹣2图象与直线y=b有两个交点,
∵当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根时,b=﹣2或b>2,
故答案为b=﹣2或b>2.
10.(2020春?南岸区校级月考)如图,抛物线y=x2+2x﹣3与x轴交于A、B两点(点A在点B的左侧),交y轴于点C,抛物线的顶点为点D.
(1)求AB的长度和点D的坐标;
(2)求直线AC的函数表达式;
(3)点P是第四象限抛物线上一点,当2S△PAC=S△PAB时,求点P的坐标.
【解答】解:(1)令y=0,得y=x2+2x﹣3=0,
解得,x=﹣3或1,
∴A(﹣3,0),B(1,0),
∴AB=1﹣(﹣3)=4,
∵y=x2+2x﹣3=(x+1)2﹣4,
∴D(﹣1,﹣4);
(2)令x=0,得y=x2+2x﹣3=﹣3,
∴C(0,﹣3),
设直线AC的解析式为y=kx+b(k≠0),得
,
解得,,
∴直线AC的解析式为:y=﹣x﹣3;
(3)设P(m,m2+2m﹣3)(0<m<1),过P作PQ⊥x轴于点Q,如下图,
则PQ=﹣m2﹣2m+3,OQ=m,AQ=m+3
∵2S△PAC=S△PAB,
∴2(S△AOC+S梯形OQPC﹣S△APQ)=S△PAB,
即=,
解得,m=﹣3(舍),m=,
∴.
11.(2020?雁塔区校级模拟)如图,直线y=﹣x﹣3与坐标轴交于点A、C,经过点A、C的抛物线.y=ax2+bx+c与x轴交于点B(2,0),点D是抛物线在第三象限图象上的动点,过点D作DE⊥x轴于点E,交AC于点F.
(1)求该二次函数的解析式;
(2)若线段AC恰好将△ADE的面积分成1:4的两部分,请求出此时点D的坐标.
【解答】解:(1)直线y=﹣x﹣3与坐标轴交于点A、C,
当x=0时,y=﹣3;当y=0时,x=﹣6,
∴A(﹣6,0),C(0,﹣3),
将A、B、C三点坐标代入抛物线的关系式得,
,解得,,
∴抛物线的关系式为y=x2+x﹣3;
(2)设点D(x,x2+x﹣3),则点F(x,﹣x﹣3)
∴DE=|x2+x﹣3|=﹣x2﹣x+3,EF=|﹣x﹣3|=x+3,
若线段AC恰好将△ADE的面积分成1:4的两部分,则EF=DE,或EF=DE,
①当EF=DE时,即x+3=(﹣x2﹣x+3),
解得,x1=﹣6,x2=﹣8,
又∵﹣6<x<0,
x1=﹣6,x2=﹣8,均不符合题意舍去,
②当EF=DE时,即x+3=(﹣x2﹣x+3),
解得,x1=﹣6,x2=﹣,
又∵﹣6<x<0,
x1=﹣6不符合题意舍去,x2=﹣,
当x=﹣时,y=×﹣﹣3=﹣,
∴点D(﹣,﹣).
12.(2020?东营)如图,抛物线y=ax2﹣3ax﹣4a的图象经过点C(0,2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的解析式及点A、B的坐标;
(2)是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
【解答】解:(1)把C(0,2)代入y=ax2﹣3ax﹣4a得:﹣4a=2.
解得a=﹣.
则该抛物线解析式为y=﹣x2+x+2.
由于y=﹣x2+x+2=﹣(x+1)(x﹣4).
故A(﹣1,0),B(4,0);
(2)存在,理由如下:
由题意知,点E位于y轴右侧,作EG∥y轴,交BC于点G,
∴CD∥EG,
∴=.
∵直线y=kx+1(k>0)与y轴交于点D,则D(0,1).
∴CD=2﹣1=1.
∴=EG.
设BC所在直线的解析式为y=mx+n(m≠0).
将B(4,0),C(0,2)代入,得.
解得.
∴直线BC的解析式是y=﹣x+2.
设E(t,﹣t2+t+2),则G(t,﹣t+2),其中0<t<4.
∴EG=(﹣t2+t+2)﹣(﹣t+2)=﹣(t﹣2)2+2.
∴=﹣(t﹣2)2+2.
∵<0,
∴当t=2时,存在最大值,最大值为2,此时点E的坐标是(2,3).
13.(2020?宿迁)某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价x(元/千克) 55 60 65 70
销售量y(千克) 70 60 50 40
(1)求y(千克)与x(元/千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
【解答】解:(1)设y与x之间的函数表达式为y=kx+b(k≠0),将表中数据(55,70)、(60,60)代入得:
,
解得:.
∴y与x之间的函数表达式为y=﹣2x+180.
(2)由题意得:(x﹣50)(﹣2x+180)=600,
整理得:x2﹣140x+4800=0,
解得x1=60,x2=80.
答:为保证某天获得600元的销售利润,则该天的销售单价应定为60元/千克或80元/千克.
(3)设当天的销售利润为w元,则:
w=(x﹣50)(﹣2x+180)
=﹣2(x﹣70)2+800,
∵﹣2<0,
∴当x=70时,w最大值=800.
答:当销售单价定为70元/千克时,才能使当天的销售利润最大,最大利润是800元.
14.(2020?随州)2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格p(元/只)和销量q(只)与第x天的关系如下表:
第x天 1 2 3 4 5
销售价格p(元/只) 2 3 4 5 6
销量q(只) 70 75 80 85 90
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元/只,该药店从第6天起将该型号口罩的价格调整为1元/只.据统计,该药店从第6天起销量q(只)与第x天的关系为q=﹣2x2+80x﹣200 (6≤x≤30,且x为整数),已知该型号口罩的进货价格为0.5元/只.
(1)直接写出该药店该月前5天的销售价格p与x和销量q与x之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润W(元)与x的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m倍的罚款,若罚款金额不低于2000元,则m的取值范围为 m≥ .
【解答】解:(1)根据表格数据可知:
前5天的某型号口罩销售价格p(元/只)和销量q(只)与第x天的关系为:
p=x+1,1≤x≤5且x为整数;
q=5x+65,1≤x≤5且x为整数;
(2)当1≤x≤5且x为整数时,
W=(x+1﹣0.5)(5x+65)
=5x2+x+;
当6≤x≤30且x为整数时,
W=(1﹣0.5)(﹣2x2+80x﹣200)
=﹣x2+40x﹣100.
即有W=,
当1≤x≤5且x为整数时,售价,销量均随x的增大而增大,
故当x=5时,W有最大值为:495元;
当6≤x≤30且x为整数时,
W═﹣x2+40x﹣100=﹣(x﹣20)2+300,
故当x=20时,W有最大值为:300元;
由495>300,可知:
第5天时利润最大为495元.
(3)根据题意可知:
获得的正常利润之外的非法所得部分为:
(2﹣0.5﹣0.5)×70+(3﹣1)×75+(4﹣1)×80+(5﹣1)×85+(6﹣1)×90=1250(元),
∴1250m≥2000,
解得m≥.
则m的取值范围为m≥.
故答案为:m≥.
15.(2020?荆门)2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为p=,销售量y(千克)与x之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
【解答】解:(1)当0<x≤20时,设y与x的函数关系式为y=ax+b,
,
解得,,
即当0<x≤20时,y与x的函数关系式为y=﹣2x+80,
当20<x≤30时,设y与x的函数关系式为y=mx+n,
,
解得,,
即当20<x≤30时,y与x的函数关系式为y=4x﹣40,
由上可得,y与x的函数关系式为y=;
(2)设当月第x天的销售额为w元,
当0<x≤20时,w=(x+4)×(﹣2x+80)=(x﹣15)2+500,
∴当x=15时,w取得最大值,此时w=500,
当20<x≤30时,w=(x+12)×(4x﹣40)=(x﹣35)2+500,
∴当x=30时,w取得最大值,此时w=480,
由上可得,当x=15时,w取得最大值,此时w=500,
答:当月第15天,该农产品的销售额最大,最大销售额是500元.
16.(2019秋?宁明县期中)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.求S与x之间的函数表达式,并求自变量x的取值范围.
【解答】解:∵AB=xm,∴BC=(28﹣x)m,
S=AB?BC=x(28﹣x)=﹣x2+28x,
∵篱笆的长为28m,∴0<x<28,
即S=﹣x2+28x(0<x<28).
17.(2020?湖州模拟)如图,已知在平面直角坐标系xOy中,直线y=x+b经过点B(1,3),且与直线y=﹣2x交于点A,抛物线y=(x﹣m)2+n的顶点在直线y=﹣2x上运动.
(1)求点A的坐标.
(2)当抛物线经过点A时,求抛物线的解析式.
(3)当﹣1<x<1时,始终满足(x﹣m)2+n<x+b,结合图象,直接写出m的取值范围.
【解答】解:(1)将点B的坐标代入y=x+b得:+b=3,解得:b=2.5,
故y=x+,
联立,解得,
故点A的坐标为(﹣1,2);
(2)∵抛物线y=(x﹣m)2+n的顶点在直线y=﹣2x上运动,则n=﹣2m,
则y=(x﹣m)2﹣2m,
将点A的坐标代入上式并解得:m=±1,
故抛物线的表达式为:y=(x﹣1)2﹣2或y=(x+1)2+2;
(3)设:y=(x﹣m)2﹣2m,y′=x+,
当﹣1<x<1时,始终满足(x﹣m)2+n<x+b,即y在y′的下方,
当x=﹣1时,y′=×(﹣1)+=2,而y=(﹣1﹣m)2﹣2m=m2+1,
即m2+1<2,解得:﹣1<m<1;
当x=1时,同理可得:y′=3,y=m2﹣4m+1,
即y=m2﹣4m+1<3,解得2﹣<m<2+;
故m的取值范围为2﹣<m<1.
18.(2020?宁波模拟)如图,抛物线y1=﹣x2﹣x+c与直线y2=x+b交于A,B(1,0)两点.
(1)分别求c,b的值.
(2)求y1﹣y2的最大值.
(3)求点A的坐标,并根据图象判断,当x取何值时,y1>y2?
【解答】解:(1)∵抛物线y1=﹣x2﹣x+c与直线y2=x+b交于A,B(1,0)两点,
∴0=﹣1﹣1+c,0=×1+b,
解得,b=﹣,c=2;
(2)∵b=﹣,c=2,
∴抛物线y1=﹣x2﹣x+2,直线y2=x﹣,
∴y1﹣y2
=(﹣x2﹣x+2)﹣(x﹣)
=﹣x2﹣x+
=﹣(x+)2+,
即当x=﹣时,y1﹣y2取得最大值,
即y1﹣y2的最大值是;
(3),
解得,或,
∴点A的坐标为(﹣,﹣),
由图象可得,
当﹣<x<1时,y1>y2.
19.(2020?镇海区模拟)如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
【解答】解:(1)∵直线y=x+m经过点A(0,3),
∴m=3,
∴直线为y=x+3,
∵二次函数y=ax2+2x+c的图象经过点A(0,3),且对称轴为直线x=1.
∴,解得,
∴二次函数解析式为y=﹣x2+2x+3;
(2)解得或,
∴B(1,4),
∴△OAB的面积==;
(3)由图象可知:当x<0或x>1时,该一次函数值大于二次函数值.
20.(2020?雅安)已知二次函数y=x2+bx+c(a≠0)的图象与x轴的交于A、B(1,0)两点,与y轴交于点C(0,﹣3),
(1)求二次函数的表达式及A点坐标;
(2)D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标;
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以M、N、B、O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
【解答】解:(1)把B(1,0),C(0,﹣3)代入y=x2+bx+c
则有,
解得
∴二次函数的解析式为y=x2+2x﹣3,
令y=0,得到x2+2x﹣3=0,解得x=﹣3或1,
∴A(﹣3,0).
(2)如图1中连接AD,CD.
∵点D到直线AC的距离取得最大,
∴此时△DAC的面积最大
设直线AC解析式为:y=kx+b,
∵A(﹣3,0),C(0,﹣3),
∴,
解得,,
∴直线AC的解析式为y=﹣x﹣3,
过点D作x轴的垂线交AC于点G,设点D的坐标为(x,x2+2x﹣3),
则G(x,﹣x﹣3),
∵点D在第三象限,
∴DG=﹣x﹣3﹣(x2+2x﹣3)=﹣x﹣3﹣x2﹣2x+3=﹣x2﹣3x,
∴S△ACD=?DG?OA=(﹣x2﹣3x)×3=﹣x2﹣=﹣(x+)2+,
∴当x=﹣时,S最大=,点D(﹣,﹣),
∴点D到直线AC的距离取得最大时,D(﹣,﹣).
(3)如图2中,当OB是平行四边形的边时,OB=MN=1,OB∥MN,可得N(﹣2,﹣3)或N′(0,﹣3),
当OB为对角线时,点N″的横坐标为2,
x=2时,y=4+4﹣3=5,
∴N″(2,5).
综上所述,满足条件的点N的坐标为(﹣2,﹣3)或(0,﹣3)或(2,5).
21.(2020?丹东)如图1,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,A点坐标为(﹣2,0),与y轴交于点C(0,4),直线y=﹣x+m与抛物线交于B,D两点.
(1)求抛物线的函数表达式.
(2)求m的值和D点坐标.
(3)点P是直线BD上方抛物线上的动点,过点P作x轴的垂线,垂足为H,交直线BD于点F,过点D作x轴的平行线,交PH于点N,当N是线段PF的三等分点时,求P点坐标.
(4)如图2,Q是x轴上一点,其坐标为(﹣,0).动点M从A出发,沿x轴正方向以每秒5个单位的速度运动,设M的运动时间为t(t>0),连接AD,过M作MG⊥AD于点G,以MG所在直线为对称轴,线段AQ经轴对称变换后的图形为A′Q′,点M在运动过程中,线段A′Q′的位置也随之变化,请直接写出运动过程中线段A′Q′与抛物线有公共点时t的取值范围.
【解答】解:(1)把A(﹣2,0),C(0,4)代入y=﹣12x2+bx+c,
得到,
解得,
∴抛物线的解析式为y=﹣x2+x+4.
(2)令y=0,则有﹣x2+x+4=0,
解得x=﹣2或4,
∴B(4,0),
把B(4,0)代入y=﹣x+m,得到m=2,
∴直线BD的解析式为y=﹣x+2,
由,解得或,
∴D(﹣1,).
(3)设P(a,﹣a2+a+4),
则N(a,),F(a,﹣a+2),
∴PN=﹣a2+a+4﹣=﹣a2+a+,NF=﹣(﹣a+2)=a+,
∵N是线段PF的三等分点,
∴PN=2NF或NF=2PN,
∴﹣a2+a+=a+1或a+=﹣a2+2a+3,
解得a=±1或﹣1或,
∵a>0,
∴a=1或,
∴P(1,)或(,).
(4)如图2中,
∵A(﹣2,0),D(﹣1,),
∴直线AD的解析式为y=x+5,
∵A′Q′与AQ关于MG对称,MG⊥AD,
∴QQ′∥AD,
∵Q(﹣,0),
∴直线QQ′的解析式为y=x+2,设直线QQ′交抛物线于E,
由,解得或,
∴E(1,),
当点A′与D重合时,直线GM的解析式为y=﹣x+,可得M(1,0),此时t=,
当点Q′与E重合时,直线GM经过点(,),
∵GM⊥AD,
∴GM的解析式为y=﹣x+,
令y=0,可得x=,
∴M(,0),此时t==,
观察图象可知,满足条件的t的值为≤t≤.
22.(2020?永州)在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,且AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知Q(1,﹣)是抛物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.
【解答】解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
在等腰Rt△ABC中,OC垂直平分AB,且AB=4,
∴OA=OB=OC=2,
∴A(﹣2,0),B(2,0),C(0,﹣2),
∴,
解得,,
∴抛物线的解析式为y=﹣2;
(2)①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2),
由,可得,
∴x1+x2=2k,x1?x2=﹣4,
∴,
∴,
∴,
∴当k=0时2取最小值为4.
∴△CMN面积的最小值为4.
②假设抛物线上存在点P(m,﹣2),使得点P与点Q关于直线l对称,
∴OP=OQ,即,
解得,,,m3=1,m4=﹣1,
∵m3=1,m4=﹣1不合题意,舍去,
当时,点P(),
线段PQ的中点为(),
∴,
∴,
∴直线l的表达式为:y=(1﹣)x,
当时,点P(﹣,﹣),
线段PQ的中点为(,﹣1),
∴,
∴,
∴直线l的解析式为y=(1+)x.
综上,直线l的解析式为y=(1﹣)x或y=(1+)x.
23.(2020?鄂尔多斯)如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数解析式;
(2)点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;
(3)如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.
【解答】解:(1)∵抛物线y=x2+bx+c交x轴于点A(1,0),与y轴交于点C(0,﹣3),
∴,
解得:,
∴抛物线解析式为:y=x2+2x﹣3;
(2)∵抛物线y=x2+2x﹣3与x轴于A,B两点,
∴点B(﹣3,0),
∵点B(﹣3,0),点C(0,﹣3),
∴OB=OC=3,
∴∠OBC=∠OCB=45°,
如图1,当点D在点C上方时,
∵∠DBC=15°,
∴∠OBD=30°,
∴tan∠DBO==,
∴OD=×3=,
∴CD=3﹣;
若点D在点C下方时,
∵∠DBC=15°,
∴∠OBD=60°,
∴tan∠DBO==,
∴OD=3,
∴DC=3﹣3,
综上所述:线段CD的长度为3﹣或3﹣3;
(3)如图2,在BO上截取OE=OA,连接CE,过点E作EF⊥AC,
∵点A(1,0),点C(0,﹣3),
∴OA=1,OC=3,
∴AC===,
∵OE=OA,∠COE=∠COA=90°,OC=OC,
∴△OCE≌△OCA(SAS),
∴∠ACO=∠ECO,CE=AC=,
∴∠ECA=2∠ACO,
∵∠PAB=2∠ACO,
∴∠PAB=∠ECA,
∵S△AEC=AE×OC=AC×EF,
∴EF==,
∴CF===,
∴tan∠ECA==,
如图2,当点P在AB的下方时,设AO与y轴交于点N,
∵∠PAB=∠ECA,
∴tan∠ECA=tan∠PAB==,
∴ON=,
∴点N(0,),
又∵点A(1,0),
∴直线AP解析式为:y=x﹣,
联立方程组得:,
解得:或,
∴点P坐标为:(﹣,﹣),
当点P在AB的上方时,同理可求直线AP解析式为:y=﹣x+,
联立方程组得:,
解得:或,
∴点P坐标为:(﹣,),
综上所述:点P的坐标为(﹣,),(﹣,﹣).
24.(2020?鄂州)如图,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C.直线y=x﹣2经过B、C两点.
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线BC及x轴分别交于点D、M.PN⊥BC,垂足为N.设M(m,0).
①点P在抛物线上运动,若P、D、M三点中恰有一点是其它两点所连线段的中点(三点重合除外).请直接写出符合条件的m的值;
②当点P在直线BC下方的抛物线上运动时,是否存在一点P,使△PNC与△AOC相似.若存在,求出点P的坐标;若不存在,请说明理由.
【解答】解:(1)针对于直线y=x﹣2,
令x=0,则y=﹣2,
∴C(0,﹣2),
令y=0,则0=x﹣2,
∴x=4,
∴B(4,0),
将点B,C坐标代入抛物线y=x2+bx+c中,得,
∴,
∴抛物线的解析式为y=x2﹣x﹣2;
(2)①∵PM⊥x轴,M(m,0),
∴P(m,m2﹣m﹣2),D(m,m﹣2),
∵P、D、M三点中恰有一点是其它两点所连线段的中点,
∴Ⅰ、当点D是PM的中点时,(0+m2﹣m﹣2)=,
∴m=﹣或m=4(此时点D,M,P三点重合,舍去),
Ⅱ、当点P是DM的中点时,(0+m﹣2)=m2﹣m﹣2,
∴m=1或m=4(此时点D,M,P三点重合,舍去),
Ⅲ、当点M是DP的中点时,(m2﹣m﹣2+m﹣2)=0,
∴m=2或m=4(此时点D,M,P三点重合,舍去),
即满足条件的m的值为﹣或1或2;
②由(1)知,抛物线的解析式为y=x2﹣x﹣2,
令y=0,则0=x2﹣x﹣2,
∴x=﹣1或x=4,
∴点A(﹣1,0),
∴OA=1,
∵B(4,0),C(0,﹣2),
∴OB=4,OC=2,
∴,
∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴∠OAC=∠OCB,∠ACO=∠OBC,
∵△PNC与△AOC相似,
∴Ⅰ、当△PNC∽△AOC,
∴∠PCN=∠ACO,
∴∠PCN=∠OBC,
∴CP∥OB,
∴点P的纵坐标为﹣2,
∴m2﹣m﹣2=﹣2,
∴m=0(舍)或m=3,
∴P(3,﹣2);
Ⅱ、当△PNC∽△COA时,
∴∠PCN=∠CAO,
∴∠OCB=∠PCD,
∵PD∥OC,
∴∠OCB=∠CDP,
∴∠PCD=∠PDC,
∴PC=PD,
由①知,P(m,m2﹣m﹣2),D(m,m﹣2),
∵C(0,﹣2),
∴PD=2m﹣m2,PC==,
∴2m2﹣m=,
∴m=,
∴P(,﹣),
即满足条件的点P的坐标为(3,﹣2)或(,﹣).
25.(2020?恩施州)如图1,抛物线y=﹣x2+bx+c经过点C(6,0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点.
(1)求抛物线的解析式;
(2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90°,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=﹣x2+bx+c只有一个交点时,求点M的坐标.
(3)△MPC在(2)的旋转变换下,若PC=(如图2).
①求证:EA=ED.
②当点E在(1)所求的抛物线上时,求线段CM的长.
【解答】解:(1)∵点C(6,0)在抛物线上,
∴,
得到6b+c=9,
又∵对称轴为x=2,
∴,
解得b=1,
∴c=3,
∴二次函数的解析式为;
(2)当点M在点C的左侧时,如图2﹣1中:
∵抛物线的解析式为,对称轴为x=2,C(6,0)
∴点A(2,0),顶点B(2,4),
∴AB=AC=4,
∴△ABC是等腰直角三角形,
∴∠1=45°;
∵将△MPC逆时针旋转90°得到△MEF,
∴FM=CM,∠2=∠1=45°,
设点M的坐标为(m,0),
∴点F(m,6﹣m),
又∵∠2=45°,
∴直线EF与x轴的夹角为45°,
∴设直线EF的解析式为y=x+b,
把点F(m,6﹣m)代入得:6﹣m=m+b,解得:b=6﹣2m,
直线EF的解析式为y=x+6﹣2m,
∵直线EF与抛物线只有一个交点,
∴,
整理得:,
∴△=b2﹣4ac=0,解得m=,
点M的坐标为(,0).
当点M在点C的右侧时,如下图:
由图可知,直线EF与x轴的夹角仍是45°,因此直线EF与抛物线不可能只有一个交点.
综上,点M的坐标为(,0).
(3)①当点M在点C的左侧时,如下图,过点P作PG⊥x轴于点G,过点E作EH⊥x轴于点H,
∵,由(2)知∠BCA=45°,
∴PG=GC=1,
∴点G(5,0),
设点M的坐标为(m,0),
∵将△MPC逆时针旋转90°得到△MEF,
∴EM=PM,
∵∠HEM+∠EMH=∠GMP+∠EMH=90°,
∴∠HEM=∠GMP,
在△EHM和△MGP中,,
∴△EHM≌△MGP(AAS),
∴EH=MG=5﹣m,HM=PG=1,
∴点H(m﹣1,0),
∴点E的坐标为(m﹣1,5﹣m);
∴EA==,
又∵D为线段BC的中点,B(2,4),C(6,0),
∴点D(4,2),
∴ED==,
∴EA=ED.
当点M在点C的右侧时,如下图:
同理,点E的坐标仍为(m﹣1,5﹣m),因此EA=ED.
②当点E在(1)所求的抛物线上时,
把E(m﹣1,5﹣m)代入,整理得:m2﹣10m+13=0,
解得:m=或m=,
∴CM=或CM=.
26.(2020?青海)如图1(注:与图2完全相同)所示,抛物线y=﹣+bx+c经过B、D两点,与x轴的另一个交点为A,与y轴相交于点C.
(1)求抛物线的解析式.
(2)设抛物线的顶点为M,求四边形ABMC的面积.(请在图1中探索)
(3)设点Q在y轴上,点P在抛物线上.要使以点A、B、P、Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)
【解答】解:(1)把B(3,0)和D(﹣2,﹣)代入抛物线的解析式得,
,
解得,,
∴抛物线的解析式为:;
(2)令x=0,得=,
∴,
令y=0,得=0,
解得,x=﹣1,或x=3,
∴A(﹣1,0),
∵=,
∴M(1,2),
∴S四边形ABMC=S△AOC+S△COM+S△MOB
=
=;
(3)设Q(0,n),
①当AB为平行四边形的边时,有AB∥PQ,AB=PQ,
a).P点在Q点左边时,则P(﹣4,n),
把P(﹣4,n)代入,得
n=,
∴P(﹣4,﹣);
②当AB为平行四边形的边时,有AB∥PQ,AB=PQ,
当P点在Q点右边时,则P(4,n),
把P(4,n)代入,得
n=,
∴P(4,﹣);
③当AB为平行四边形的对角线时,如图2,AB与PQ交于点E,
则E(1,0),
∵PE=QE,
∴P(2,﹣n),
把P(2,﹣n)代入,得
﹣n=,
∴n=﹣,
∴P(2,).
综上,满足条件的P点坐标为:(﹣4,﹣)或(4,﹣)或(2,).
27.(2020?山西)综合与探究
如图,抛物线y=x2﹣x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为(4,﹣3).
(1)请直接写出A,B两点的坐标及直线l的函数表达式;
(2)若点P是抛物线上的点,点P的横坐标为m(m≥0),过点P作PM⊥x轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标;
(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.
【解答】解:(1)令y=0,得y=x2﹣x﹣3=0,
解得,x=﹣2,或x=6,
∴A(﹣2,0),B(6,0),
设直线l的解析式为y=kx+b(k≠0),则
,
解得,,
∴直线l的解析式为;
(2)如图1,根据题意可知,点P与点N的坐标分别为
P(m,m2﹣m﹣3),N(m,m﹣1),
∴PM=﹣m2+m+3,MN=m+1,NP=﹣m2+m+2,
分两种情况:
①当PM=3MN时,得﹣m2+m+3=3(m+1),
解得,m=0,或m=﹣2(舍),
∴P(0,﹣3);
②当PM=3NP时,得﹣m2+m+3=3(﹣m2+m+2),
解得,m=3,或m=﹣2(舍),
∴P(3,﹣);
∴当点N是线段PM的三等分点时,点P的坐标为(3,﹣)或(0,﹣3);
(3)∵直线l:与y轴于点E,
∴点E的坐标为(0,﹣1),
分再种情况:①如图2,当点Q在y轴的正半轴上时,记为点Q1,
过Q1作Q1H⊥AD于点H,则∠Q1HE=∠AOE=90°,
∵∠Q1EH=∠AEO,
∴△Q1EH∽△AEO,
∴,即
∴Q1H=2HE,
∵∠Q1DH=45°,∠Q1HD=90°,
∴Q1H=DH,
∴DH=2EH,
∴HE=ED,
连接CD,
∵C(0,﹣3),D(4,﹣3),
∴CD⊥y轴,
∴ED=,
∴,,
∴,
∴Q1O=Q1E﹣OE=9,
∴Q1(0,9);
②如图3,当点Q在y轴的负半轴上时,记为点Q2,过Q2作Q2G⊥AD于G,则∠Q2GE=∠AOE=90°,
∵∠Q2EG=∠AEO,
∴△Q2GE∽△AOE,
∴,即,
∴Q2G=2EG,
∵∠Q2DG=45°,∠Q2GD=90°,
∴∠DQ2G=∠Q2DG=45°,
∴DG=Q2G=2EG,
∴ED=EG+DG=3EG,
由①可知,ED=2,
∴3EG=2,
∴,
∴,
∴,
∴,
,
综上,点Q的坐标为(0,9)或(0,﹣).
28.(2020?淄博)如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx+(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是?OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
【解答】解:(1)OA=2=BC,故函数的对称轴为x=1,则x=﹣=1①,
将点A的坐标代入抛物线表达式得:0=4a﹣2b+②,
联立①②并解得,
故抛物线的表达式为:y=﹣x2+x+③;
(2)∵y=﹣x2+x+=﹣(x﹣1)2+3,
∴抛物线的顶点M(1,3)
令y=0,可得x=﹣2或4,
∴点D(4,0);
∵△ADR的面积是?OABC的面积的,
∴×AD×|yR|=×OA×OB,则×6×|yR|=×2×,解得:yR=±④,
联立④③并解得或,
故点R的坐标为(1+,﹣)或(1,﹣)或(1,)或(1﹣,);
(3)①当点P与M重合时,存在唯一的点Q(4,0)与D重合,此时符合题意,P(1,3).
②根据对称性可知.P(1,﹣3),Q与D重合时,也符合题意.
③当点P是EM的中点,点Q是DM的中点时,也符合题意,此时P(1,)
综上所述,满足条件的点P的坐标为(1,3)或(1,﹣3)或(1,).
29.(2020?青岛)某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
(1)按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k≠0)表示.求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2.已知GM=2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)
(3)根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
【解答】解:(1)∵长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
∴OH=AB=3,
∴EO=EH﹣OH=4﹣3=1,
∴E(0,1),D(2,0),
∴该抛物线的函数表达式为:y=kx2+1,
把点D(2,0)代入,得k=﹣,
∴该抛物线的函数表达式为:y=﹣x2+1;
(2)∵GM=2,
∴OM=OG=1,
∴当x=1时,y=,
∴N(1,),
∴MN=,
∴S矩形MNFG=MN?GM=×2=,
∴每个B型活动板房的成本是:
425+×50=500(元).
答:每个B型活动板房的成本是500元;
(3)根据题意,得
w=(n﹣500)[100+]
=﹣2(n﹣600)2+20000,
∵每月最多能生产160个B型活动板房,
∴100+≤160,
解得n≥620,
∵﹣2<0,
∴n≥620时,w随n的增大而减小,
∴当n=620时,w有最大值为19200元.
答:公司将销售单价n(元)定为620元时,每月销售B型活动板房所获利润w(元)最大,最大利润是19200元.
30.(2020?咸宁)如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n<)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
【解答】解:(1)直线y=﹣x+2与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为(4,0)、(0,2),
将点B、C的坐标代入抛物线表达式得,解得,
故抛物线的表达式为:y=﹣x2+x+2①;
(2)如图1,作点B关于x轴的对称点B′(0,﹣2),连接AB′交抛物线于点P(P′),则∠PAO=∠BAO,
设直线AB'的解析式为y=kx+m,
∴,
∴,
直线AB′的表达式为:y=x﹣2②,
联立①②并解得:x=3或﹣2,
故点P的坐标为(3,﹣)或(﹣2,﹣3),
当点P与B,C重合时,也满足条件,此时P(0,2)或(,),
综上所述,满足条件的点P的坐标为(3,﹣)或(﹣2,﹣3)或(0,2)或(,).
(3)①过点C作CH⊥x轴于点H,
∵∠MNC=90°,
∴∠MNO+∠CNH=90°,
又∵∠CNH+∠NCH=90°,
∴∠MNO=∠NCH,
∴tan∠MNO=tan∠NCH,即,即,
解得:m=﹣n2+n;
②m=﹣n2+n,
∵<0,故m有最大值,当n=时,m的最大值为,
而m>0,
故0<m<时,符合条件的N点的个数有2个.
_21?????????è?????(www.21cnjy.com)_
浙教版九年级(上)二次函数的运用
一、解答题(共30小题)
1.(2020?攀枝花)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
2.(2020?宜兴市一模)在平面直角坐标系中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且S△ABC:S△BCE=3:4.
(1)求点A,点B的坐标;
(2)将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
①求直线CE的解析式;
②求抛物线的解析式.
3.(2020?沭阳县模拟)“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降2元,则每月可多销售10条,设每条裤子的售价为x元(x为正整数),每月的销售量为y条.
(1)直接写出y与x的函数关系式;
(2)设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润不低于4175元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
4.(2020?溧阳市模拟)如图,已知二次函数y=x2+bx的图象经过点A(﹣4,0),顶点为B,一次函数y=x+2的图象交y轴于点M,P是抛物线上一点,点M关于直线AP的对称点N恰好落在抛物线的对称轴直线BH上(对称轴直线BH与x轴交于点H).
(1)求二次函数的表达式;
(2)求点P的坐标;
(3)若点G是第二象限内抛物线上一点,G关于抛物线的对称轴的对称点是E,连接OG,点F是线段OG上一点,点D是坐标平面内一点,若四边形BDEF是正方形,求点G的坐标.
5.(2020?孝南区二模)已知抛物线y=ax2+bx﹣6与x轴交于A(﹣2,0),B(3,0)两点,与y轴交于点C,连结BC.
(1)填空:a= ,b= ;
(2)如图1,若D为抛物线上BC下方一动点(不与C,B重合),连OD交BC于E,求的最大值;
(3)如图2,点P在抛物线上,且∠BCO=∠PBA,请直接写出P点的坐标.
6.(2020?沭阳县模拟)如图1,在平面直角坐标系中,已知点A的坐标是(3,0),并且OA=OC=3OB,动点P在过A,B,C三点的抛物线上,
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为底的等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,以线段EF的中点G为圆心,以EF为直径作⊙G,求⊙G最小面积.
7.(2020?朝阳区校级一模)在平面直角坐标系中,记函数y=的图象为G,正方形ABCD的对称中心与原点重合,顶点A的坐标为(2,2),点B在第四象限.
(1)当n=1时.
①求G的最低点的纵坐标;
②求图象G上所有到x轴的距离为2的横坐标之和.
③若当a≤x≤b时,﹣9≤y≤2,则a、b的对应值为 .
(2)当图象G与正方形ABCD的边恰好有两个公共点时,直接写出n的取值范围.
8.(2020?清江浦区二模)在平面直角坐标系中,Rt△ABC,∠ACB=90°,AB∥x轴,如图1,C(1,0),且OC:OA=AC:BC=1:2.
(1)A点坐标为 ,B点坐标为 ;
(2)求过A、B、C三点的抛物线表达式;
(3)如图2,抛物线对称轴与AB交于点D,现有一点P从点A出发,以每秒1个单位的速度在AB上向点B运动,另一点Q从点D与点P同时出发,以每秒5个单位在抛物线对称轴上运动.当点P到达B点时,点P、Q同时停止运动,问点P、Q运动到何处时,△PQB面积最大,试求出最大面积.
9.(2019秋?灵石县期末)借鉴我们已有研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象与性质,研究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 …
y … 10 m ﹣2 1 n 1 ﹣2 3 10 …
其中,m= ,n= ;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①写出函数的一条图象性质: ;
②当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根,根据函数图象直接写出的取值范围为 .
10.(2020春?南岸区校级月考)如图,抛物线y=x2+2x﹣3与x轴交于A、B两点(点A在点B的左侧),交y轴于点C,抛物线的顶点为点D.
(1)求AB的长度和点D的坐标;
(2)求直线AC的函数表达式;
(3)点P是第四象限抛物线上一点,当2S△PAC=S△PAB时,求点P的坐标.
11.(2020?雁塔区校级模拟)如图,直线y=﹣x﹣3与坐标轴交于点A、C,经过点A、C的抛物线.y=ax2+bx+c与x轴交于点B(2,0),点D是抛物线在第三象限图象上的动点,过点D作DE⊥x轴于点E,交AC于点F.
(1)求该二次函数的解析式;
(2)若线段AC恰好将△ADE的面积分成1:4的两部分,请求出此时点D的坐标.
12.(2020?东营)如图,抛物线y=ax2﹣3ax﹣4a的图象经过点C(0,2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的解析式及点A、B的坐标;
(2)是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
13.(2020?宿迁)某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价x(元/千克) 55 60 65 70
销售量y(千克) 70 60 50 40
(1)求y(千克)与x(元/千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
14.(2020?随州)2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格p(元/只)和销量q(只)与第x天的关系如下表:
第x天 1 2 3 4 5
销售价格p(元/只) 2 3 4 5 6
销量q(只) 70 75 80 85 90
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元/只,该药店从第6天起将该型号口罩的价格调整为1元/只.据统计,该药店从第6天起销量q(只)与第x天的关系为q=﹣2x2+80x﹣200 (6≤x≤30,且x为整数),已知该型号口罩的进货价格为0.5元/只.
(1)直接写出该药店该月前5天的销售价格p与x和销量q与x之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润W(元)与x的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m倍的罚款,若罚款金额不低于2000元,则m的取值范围为 .
15.(2020?荆门)2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为p=,销售量y(千克)与x之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
16.(2019秋?宁明县期中)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.求S与x之间的函数表达式,并求自变量x的取值范围.
17.(2020?湖州模拟)如图,已知在平面直角坐标系xOy中,直线y=x+b经过点B(1,3),且与直线y=﹣2x交于点A,抛物线y=(x﹣m)2+n的顶点在直线y=﹣2x上运动.
(1)求点A的坐标.
(2)当抛物线经过点A时,求抛物线的解析式.
(3)当﹣1<x<1时,始终满足(x﹣m)2+n<x+b,结合图象,直接写出m的取值范围.
18.(2020?宁波模拟)如图,抛物线y1=﹣x2﹣x+c与直线y2=x+b交于A,B(1,0)两点.
(1)分别求c,b的值.
(2)求y1﹣y2的最大值.
(3)求点A的坐标,并根据图象判断,当x取何值时,y1>y2?
19.(2020?镇海区模拟)如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
20.(2020?雅安)已知二次函数y=x2+bx+c(a≠0)的图象与x轴的交于A、B(1,0)两点,与y轴交于点C(0,﹣3),
(1)求二次函数的表达式及A点坐标;
(2)D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标;
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以M、N、B、O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
21.(2020?丹东)如图1,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,A点坐标为(﹣2,0),与y轴交于点C(0,4),直线y=﹣x+m与抛物线交于B,D两点.
(1)求抛物线的函数表达式.
(2)求m的值和D点坐标.
(3)点P是直线BD上方抛物线上的动点,过点P作x轴的垂线,垂足为H,交直线BD于点F,过点D作x轴的平行线,交PH于点N,当N是线段PF的三等分点时,求P点坐标.
(4)如图2,Q是x轴上一点,其坐标为(﹣,0).动点M从A出发,沿x轴正方向以每秒5个单位的速度运动,设M的运动时间为t(t>0),连接AD,过M作MG⊥AD于点G,以MG所在直线为对称轴,线段AQ经轴对称变换后的图形为A′Q′,点M在运动过程中,线段A′Q′的位置也随之变化,请直接写出运动过程中线段A′Q′与抛物线有公共点时t的取值范围.
22.(2020?永州)在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,且AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知Q(1,﹣)是抛物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.
23.(2020?鄂尔多斯)如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数解析式;
(2)点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;
(3)如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.
24.(2020?鄂州)如图,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C.直线y=x﹣2经过B、C两点.
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线BC及x轴分别交于点D、M.PN⊥BC,垂足为N.设M(m,0).
①点P在抛物线上运动,若P、D、M三点中恰有一点是其它两点所连线段的中点(三点重合除外).请直接写出符合条件的m的值;
②当点P在直线BC下方的抛物线上运动时,是否存在一点P,使△PNC与△AOC相似.若存在,求出点P的坐标;若不存在,请说明理由.
25.(2020?恩施州)如图1,抛物线y=﹣x2+bx+c经过点C(6,0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点.
(1)求抛物线的解析式;
(2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90°,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=﹣x2+bx+c只有一个交点时,求点M的坐标.
(3)△MPC在(2)的旋转变换下,若PC=(如图2).
①求证:EA=ED.
②当点E在(1)所求的抛物线上时,求线段CM的长.
26.(2020?青海)如图1(注:与图2完全相同)所示,抛物线y=﹣+bx+c经过B、D两点,与x轴的另一个交点为A,与y轴相交于点C.
(1)求抛物线的解析式.
(2)设抛物线的顶点为M,求四边形ABMC的面积.(请在图1中探索)
(3)设点Q在y轴上,点P在抛物线上.要使以点A、B、P、Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)
27.(2020?山西)综合与探究
如图,抛物线y=x2﹣x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为(4,﹣3).
(1)请直接写出A,B两点的坐标及直线l的函数表达式;
(2)若点P是抛物线上的点,点P的横坐标为m(m≥0),过点P作PM⊥x轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标;
(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.
28.(2020?淄博)如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx+(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是?OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
29.(2020?青岛)某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
(1)按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k≠0)表示.求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2.已知GM=2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)
(3)根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
30.(2020?咸宁)如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n<)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
二次函数的运用
参考答案与试题解析
一.选择题
二.解答题(共31小题)
1.(2020?攀枝花)如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
【解答】解:(1)∵A(﹣1,0),B(2,0),C(0,4),
设抛物线表达式为:y=a(x+1)(x﹣2),
将C代入得:4=﹣2a,
解得:a=﹣2,
∴该抛物线的解析式为:y=﹣2(x+1)(x﹣2)=﹣2x2+2x+4;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,
∵A(﹣1,0),B(2,0),C(0,4),
可得:OA=1,OC=4,OB=2,
∴S=S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(﹣2m2+2m+4)
=﹣2m2+4m+6
=﹣2(m﹣1)2+8,
当m=1时,S最大,最大值为8.
2.(2020?宜兴市一模)在平面直角坐标系中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A,B两点,点B在点A的右侧,顶点为C,抛物线与y轴交于点D,直线CA交y轴于E,且S△ABC:S△BCE=3:4.
(1)求点A,点B的坐标;
(2)将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
①求直线CE的解析式;
②求抛物线的解析式.
【解答】解:(1)如图,过点C作CF⊥AB于F,
∵抛物线y=mx2﹣4mx+n(m>0),
∴对称轴为直线x=2,
∴AF=BF,点F(2,0),即OF=2,
∵S△ABC:S△BCE=3:4,
∴S△ABC=3S△ABE,
∴3××AB×OE=AB×CF,
∴CF=3OE,
∵CF⊥AB,OE⊥AB,
∴CF∥OE,
∴,
∴AF=3OA,
∵OF=OA+AF=2,
∴OA=,AF=,
∴点A坐标为(,0),
∵AB=2AF=3,
∴OB=,
∴点B坐标为(,0);
(2)①∵抛物线y=mx2﹣4mx+n(m>0)过点A(,0),
∴0=m﹣2m+n,
∴n=m,
∴y=mx2﹣4mx+n=m(x﹣2)2﹣m,
∴点C(2,﹣m),
如图2,过点C作CF⊥OB于F,CH⊥y轴于H,
又∵∠FOH=90°,
∴四边形OFCH是矩形,
∴CF=OH=m,
∵将△BCO绕点C逆时针旋转一定角度后,点B与点A重合,点O恰好落在y轴上,
∴OC=O'C,OB=O'A=,
又∵CH⊥OO',
∴OO'=2OH=m,
∵OA2+O'O2=O'A2,
∴+m2=,
∴m=,
∴点C坐标为(2,﹣),
设直线CE的解析式为y=kx+b,
∴,
解得:
∴直线CE的解析式为y=﹣x+;
②∵m=,
∴y=x2﹣x+.
3.(2020?沭阳县模拟)“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降2元,则每月可多销售10条,设每条裤子的售价为x元(x为正整数),每月的销售量为y条.
(1)直接写出y与x的函数关系式;
(2)设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润不低于4175元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
【解答】解:(1)由题意可得:
y=100+×10
=100+5(80﹣x)
=﹣5x+500,
∴y与x的函数关系式为:y=﹣5x+500;
(2)由题意得:
w=(x﹣40)(﹣5x+500)
=﹣5x2+700x﹣20000
=﹣5(x﹣70)2+4500,
∵a=﹣5<0,
∴当x=70时,w有最大利润,最大利润是4500元;
∴应降价80﹣70=10(元).
∴当销售单价降低10元时,每月获得的利润最大,最大利润是4500元;
(3)由题意得:﹣5(x﹣70)2+4500=4175+200,
解得:x1=65,x2=75,
∵抛物线开口向下,对称轴为直线x=70,
∴当65≤x≤75时,符合该网店要求,
而为了让顾客得到最大实惠,故x=65.
∴当销售单价定为65元时,既符合网店要求,又能让顾客得到最大实惠.
4.(2020?溧阳市模拟)如图,已知二次函数y=x2+bx的图象经过点A(﹣4,0),顶点为B,一次函数y=x+2的图象交y轴于点M,P是抛物线上一点,点M关于直线AP的对称点N恰好落在抛物线的对称轴直线BH上(对称轴直线BH与x轴交于点H).
(1)求二次函数的表达式;
(2)求点P的坐标;
(3)若点G是第二象限内抛物线上一点,G关于抛物线的对称轴的对称点是E,连接OG,点F是线段OG上一点,点D是坐标平面内一点,若四边形BDEF是正方形,求点G的坐标.
【解答】解:(1)∵二次函数y=x2+bx的图象经过点A(﹣4,0),
∴0=8﹣4b,
∴b=2,
∴二次函数的解析式为y=x2+2x.
(2)如图1中,当点P在第一象限时,
由题意A(﹣4,0),H(﹣2,0),M(0,2),
∵点M,K关于AP对称,
∴AK=AM==2,
∴KH==4,
∴K(﹣2,4),
∴直线MK的解析式为y=﹣x+2,
∵PA⊥MK,
∴直线PA的解析式为y=x+4,
由,解得或,
∴P(2,6).
如图2中,当点P在第三象限时,同法可得K(﹣2,﹣4),
∴直线MK的解析式为y=3x+2,
∵AP⊥MK,
∴直线AP的解析式为y=﹣x﹣,
由,解得或﹣,
∴P(﹣,﹣),
综上所述,满足条件的点P坐标为(2,6)或(﹣,﹣).
(3)如图3中,设G(m,m2+2m),过点F作FN⊥GE于N,过点F作FP⊥BH于P,设直线BH交GE于Q,设GE交y轴于K.
∵四边形EFBD是正方形,
∴EF=BF,∠EFB=90°,
∵∠ENF=∠FPB=90°,∠PNQ=∠FPQ=∠NQP=90°,
∴四边形PFNQ是矩形,
∴∠NFP=∠EFB,
∴∠EFN=∠BFP,
∴△ENF≌△BPF(AAS),
∴PF=FN,EN=BP,
∴四边形PFNQ是正方形,设PF=FN=NQ=PQ=a,
∵PN∥OK,
∴=,
∴=,
∴GN=﹣,
∵NE=PB,
∴﹣2﹣m+a=﹣4﹣m+=m2+2m﹣a,
解得m=﹣6或﹣4(舍弃),
∴G(﹣6,6).
5.(2020?孝南区二模)已知抛物线y=ax2+bx﹣6与x轴交于A(﹣2,0),B(3,0)两点,与y轴交于点C,连结BC.
(1)填空:a= 1 ,b= 1 ;
(2)如图1,若D为抛物线上BC下方一动点(不与C,B重合),连OD交BC于E,求的最大值;
(3)如图2,点P在抛物线上,且∠BCO=∠PBA,请直接写出P点的坐标.
【解答】解:(1)∵抛物线y=ax2+bx﹣6与x轴交于A(﹣2,0),B(3,0)两点,
∴,
解得,,
故答案为:1,﹣1;
(2)如图,过D点作DH⊥x轴,垂足为H,交BC于点F,
在y=x2﹣x﹣6中,当x=0时,y=﹣6,
∴C(0,﹣6),
设直线BC解析式为:y=kx+b,
把(3,0),(0,﹣6)代入得:
,解得,,
∴直线BC的解析式为y=2x﹣6,
设D(x,x2﹣x﹣6),F(x,2x﹣6),
∴OC=6,DF=2x﹣6﹣(x2﹣x﹣6)=﹣x2+3x,
又∵DH⊥x轴,
∴DH∥y轴,
∴△DEF∽△OEC,
∴,
设的比值为W,
则W===( x2 ﹣3x)=(x)2+,
∴当x=时,W有最大值,最大值为,
∴的最大值为;
(3)如图,作BC的垂直平分线交y轴于点D,连接BD,则有DC=DB,
∴∠DCB=∠DBC,
∴∠BDO=2∠BCO,
再在y轴正半轴上取一点E,使∠EBO=∠BDO,
∴∠EBO=2∠BCO,
又∵∠BCO=∠PBA,
∴直线BE与抛物线交于点P,
∵A(﹣2,0),B(3,0),C(0,﹣6),
∴OA=2,OB=3,OC=6,
设CD=BD=x,OD=6﹣x,
∴(6﹣x)2+32=x2
x=,
∴OD=,
又∵∠BOD=∠BOE=90°,
∴△BOD∽△EOB
∴,
∴,
∴OE=4,
①设直线BE解析式为y=kx+b,把(3,0),(0,4)代入得,
,解得,,
∴直线BE的解析式为 y=﹣+4,
∴,
解得,x1=,x2=3(舍去),
∴点P的坐标为(﹣,);
②若E点在y轴负半轴上,则坐标为(0,﹣4),直线BE解析式为y=x﹣4,
则可得方程组
,
解得:x3=﹣,x4=3(舍去),
∴点P的坐标为(﹣,﹣),
综上所述点P的坐标为(﹣,)或(﹣,﹣).
6.(2020?沭阳县模拟)如图1,在平面直角坐标系中,已知点A的坐标是(3,0),并且OA=OC=3OB,动点P在过A,B,C三点的抛物线上,
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为底的等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,以线段EF的中点G为圆心,以EF为直径作⊙G,求⊙G最小面积.
【解答】解:(1)∵点A的坐标是(3,0),
∴OA=3,
∵OA=OC=3OB,
∴OC=3,OB=1,
∴点C(0,3),点B(﹣1,0),
设抛物线的解析式为:y=a(x+1)(x﹣3),
∴3=﹣3a,
∴a=﹣1,
∴抛物线解析式为:y=﹣(x+1)(x﹣3)=﹣x2+2x+3;
(2)∵△ACP是以AC为底的等腰三角形,
∴AP=CP,
又∵OA=OC,
∴OP是AC的垂直平分线,
∵OA=OC,∠AOC=90°,OP是AC的垂直平分线,
∴OP平分∠AOC,
∴直线OP解析式为y=x,
联立方程组可得:,
∴或,
∴点P坐标为(,)或(,);
(3)如图,
∵点A的坐标是(3,0),点C坐标为(0,3),
∴直线AC解析式为:y=﹣x+3,
设点D坐标为(m,﹣m+3),
∴DE=|m|,DF=|﹣m+3|,
∴EF2=DE2+DF2=m2+(﹣m+3)2,
∵⊙G的面积=×EF2=×[m2+(﹣m+3)2]=×[2(m﹣)2+],
∴当m=时,⊙G最小面积为.
7.(2020?朝阳区校级一模)在平面直角坐标系中,记函数y=的图象为G,正方形ABCD的对称中心与原点重合,顶点A的坐标为(2,2),点B在第四象限.
(1)当n=1时.
①求G的最低点的纵坐标;
②求图象G上所有到x轴的距离为2的横坐标之和.
③若当a≤x≤b时,﹣9≤y≤2,则a、b的对应值为 a=﹣2,b=3或a=3,b=3+或a=﹣2,b=3+ .
(2)当图象G与正方形ABCD的边恰好有两个公共点时,直接写出n的取值范围.
【解答】解:(1)①y=,
函数图象如图所示:
函数最低点的坐标(3,﹣9),
∴图象G的最低点的纵坐标为﹣9.
②当y=2时,x2+2x+2=2,解得x=﹣2或0(舍弃)
x2﹣6x=2时,解得x=3+或3﹣(舍弃),
当y=﹣2时,x2﹣6x=﹣2,解得x=3+或3﹣,
∴图象G上所有到x轴的距离为2的横坐标之和=﹣2+3++3++3﹣=7+.
③观察图象可知:当﹣2≤x≤3或3≤x≤3+或﹣2≤x≤3+时,﹣9≤y≤2,
∴a=﹣2,b=3或a=3,b=3+或a=﹣2,b=3+.
故答案为:a=﹣2,b=3或a=3,b=3+或a=﹣2,b=3+.
(2)当y=x2+2nx+2n2的顶点落在AD边上时,n2=2,解得n=或﹣(舍弃)
当n=时,y=x2+2nx+2n2(x<0)与边AD有一个交点,y=x2﹣6nx与边BC有一个交点,符合题意.
当2n2≤2,解得n≤1或n≥﹣1,
当y=x2﹣6nx经过(2,﹣2)时,n=,
观察图象可知当<n≤1时,满足条件,
当y=x2﹣6nx的顶点在BC边上时,﹣9n2=﹣2,
解得n=或﹣(舍弃),
当n=﹣1时,y=x2+2nx+2n2(x<0)与正方形的边没有交点,
观察图象可知当﹣1<n<时,满足条件,
综上所述,满足条件的n的值为﹣1<n<或<n≤1或n=.
8.(2020?清江浦区二模)在平面直角坐标系中,Rt△ABC,∠ACB=90°,AB∥x轴,如图1,C(1,0),且OC:OA=AC:BC=1:2.
(1)A点坐标为 (0,2) ,B点坐标为 (5,2) ;
(2)求过A、B、C三点的抛物线表达式;
(3)如图2,抛物线对称轴与AB交于点D,现有一点P从点A出发,以每秒1个单位的速度在AB上向点B运动,另一点Q从点D与点P同时出发,以每秒5个单位在抛物线对称轴上运动.当点P到达B点时,点P、Q同时停止运动,问点P、Q运动到何处时,△PQB面积最大,试求出最大面积.
【解答】解:(1)∵C(1,0),
∴OC=1,
∵OC:OA=1:2,
∴OA=2,
∴A(0,2),
∴AC==,
∵AC:BC=1:2,
∴BC=2,
∵∠ACB=90°,
∴AB===5,
∵AB∥x轴,
∴B(5,2),
故答案为:(0,2),(5,2);
(2)设过A、B、C三点的抛物线表达式为:y=ax2+bx+c,
则,
解得:,
∴过A、B、C三点的抛物线表达式为:y=x2﹣x+2;
(3)如图2,设运动t秒时,△PQB面积最大,且0≤t≤5,则BP=5﹣t,DQ=5t,
∴S△PQB===﹣,
∵a=﹣<0
∴当t=﹣=时,面积最大值是:S△PQB=﹣=,
此时点P的坐标为(,2),
当点Q向上运动时,点Q的坐标为(,),
当点Q向下运动时,点Q的坐标为(,﹣),
综上,当点P的坐标为(,2),点Q的坐标为(,)或(,﹣)时,△PQB面积最大,最大面积为.
9.(2019秋?灵石县期末)借鉴我们已有研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象与性质,研究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 …
y … 10 m ﹣2 1 n 1 ﹣2 3 10 …
其中,m= 3 ,n= 2 ;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①写出函数的一条图象性质: 图象具有对称性,对称轴是直线x=1 ;
②当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根,根据函数图象直接写出的取值范围为 b=﹣2或b>2 .
【解答】解:(1)把x=﹣2代入y=|x2﹣2x﹣3|﹣2,得y=3,
∴m=3,
把x=1代入y=|x2﹣2x﹣3|﹣2,得y=2,
∴n=2,
故答案为:3,2;
(2)如图所示;
(3)①函数的性质:图象具有对称性,对称轴是直线x=1;
故答案为图象具有对称性,对称轴是直线x=1:
②由图象可知,当b=﹣2或b>2时,函数y=|x2﹣2x﹣3|﹣2图象与直线y=b有两个交点,
∵当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根时,b=﹣2或b>2,
故答案为b=﹣2或b>2.
10.(2020春?南岸区校级月考)如图,抛物线y=x2+2x﹣3与x轴交于A、B两点(点A在点B的左侧),交y轴于点C,抛物线的顶点为点D.
(1)求AB的长度和点D的坐标;
(2)求直线AC的函数表达式;
(3)点P是第四象限抛物线上一点,当2S△PAC=S△PAB时,求点P的坐标.
【解答】解:(1)令y=0,得y=x2+2x﹣3=0,
解得,x=﹣3或1,
∴A(﹣3,0),B(1,0),
∴AB=1﹣(﹣3)=4,
∵y=x2+2x﹣3=(x+1)2﹣4,
∴D(﹣1,﹣4);
(2)令x=0,得y=x2+2x﹣3=﹣3,
∴C(0,﹣3),
设直线AC的解析式为y=kx+b(k≠0),得
,
解得,,
∴直线AC的解析式为:y=﹣x﹣3;
(3)设P(m,m2+2m﹣3)(0<m<1),过P作PQ⊥x轴于点Q,如下图,
则PQ=﹣m2﹣2m+3,OQ=m,AQ=m+3
∵2S△PAC=S△PAB,
∴2(S△AOC+S梯形OQPC﹣S△APQ)=S△PAB,
即=,
解得,m=﹣3(舍),m=,
∴.
11.(2020?雁塔区校级模拟)如图,直线y=﹣x﹣3与坐标轴交于点A、C,经过点A、C的抛物线.y=ax2+bx+c与x轴交于点B(2,0),点D是抛物线在第三象限图象上的动点,过点D作DE⊥x轴于点E,交AC于点F.
(1)求该二次函数的解析式;
(2)若线段AC恰好将△ADE的面积分成1:4的两部分,请求出此时点D的坐标.
【解答】解:(1)直线y=﹣x﹣3与坐标轴交于点A、C,
当x=0时,y=﹣3;当y=0时,x=﹣6,
∴A(﹣6,0),C(0,﹣3),
将A、B、C三点坐标代入抛物线的关系式得,
,解得,,
∴抛物线的关系式为y=x2+x﹣3;
(2)设点D(x,x2+x﹣3),则点F(x,﹣x﹣3)
∴DE=|x2+x﹣3|=﹣x2﹣x+3,EF=|﹣x﹣3|=x+3,
若线段AC恰好将△ADE的面积分成1:4的两部分,则EF=DE,或EF=DE,
①当EF=DE时,即x+3=(﹣x2﹣x+3),
解得,x1=﹣6,x2=﹣8,
又∵﹣6<x<0,
x1=﹣6,x2=﹣8,均不符合题意舍去,
②当EF=DE时,即x+3=(﹣x2﹣x+3),
解得,x1=﹣6,x2=﹣,
又∵﹣6<x<0,
x1=﹣6不符合题意舍去,x2=﹣,
当x=﹣时,y=×﹣﹣3=﹣,
∴点D(﹣,﹣).
12.(2020?东营)如图,抛物线y=ax2﹣3ax﹣4a的图象经过点C(0,2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的解析式及点A、B的坐标;
(2)是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
【解答】解:(1)把C(0,2)代入y=ax2﹣3ax﹣4a得:﹣4a=2.
解得a=﹣.
则该抛物线解析式为y=﹣x2+x+2.
由于y=﹣x2+x+2=﹣(x+1)(x﹣4).
故A(﹣1,0),B(4,0);
(2)存在,理由如下:
由题意知,点E位于y轴右侧,作EG∥y轴,交BC于点G,
∴CD∥EG,
∴=.
∵直线y=kx+1(k>0)与y轴交于点D,则D(0,1).
∴CD=2﹣1=1.
∴=EG.
设BC所在直线的解析式为y=mx+n(m≠0).
将B(4,0),C(0,2)代入,得.
解得.
∴直线BC的解析式是y=﹣x+2.
设E(t,﹣t2+t+2),则G(t,﹣t+2),其中0<t<4.
∴EG=(﹣t2+t+2)﹣(﹣t+2)=﹣(t﹣2)2+2.
∴=﹣(t﹣2)2+2.
∵<0,
∴当t=2时,存在最大值,最大值为2,此时点E的坐标是(2,3).
13.(2020?宿迁)某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价x(元/千克) 55 60 65 70
销售量y(千克) 70 60 50 40
(1)求y(千克)与x(元/千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
【解答】解:(1)设y与x之间的函数表达式为y=kx+b(k≠0),将表中数据(55,70)、(60,60)代入得:
,
解得:.
∴y与x之间的函数表达式为y=﹣2x+180.
(2)由题意得:(x﹣50)(﹣2x+180)=600,
整理得:x2﹣140x+4800=0,
解得x1=60,x2=80.
答:为保证某天获得600元的销售利润,则该天的销售单价应定为60元/千克或80元/千克.
(3)设当天的销售利润为w元,则:
w=(x﹣50)(﹣2x+180)
=﹣2(x﹣70)2+800,
∵﹣2<0,
∴当x=70时,w最大值=800.
答:当销售单价定为70元/千克时,才能使当天的销售利润最大,最大利润是800元.
14.(2020?随州)2020年新冠肺炎疫情期间,部分药店趁机将口罩涨价,经调查发现某药店某月(按30天计)前5天的某型号口罩销售价格p(元/只)和销量q(只)与第x天的关系如下表:
第x天 1 2 3 4 5
销售价格p(元/只) 2 3 4 5 6
销量q(只) 70 75 80 85 90
物价部门发现这种乱象后,统一规定各药店该型号口罩的销售价格不得高于1元/只,该药店从第6天起将该型号口罩的价格调整为1元/只.据统计,该药店从第6天起销量q(只)与第x天的关系为q=﹣2x2+80x﹣200 (6≤x≤30,且x为整数),已知该型号口罩的进货价格为0.5元/只.
(1)直接写出该药店该月前5天的销售价格p与x和销量q与x之间的函数关系式;
(2)求该药店该月销售该型号口罩获得的利润W(元)与x的函数关系式,并判断第几天的利润最大;
(3)物价部门为了进一步加强市场整顿,对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m倍的罚款,若罚款金额不低于2000元,则m的取值范围为 m≥ .
【解答】解:(1)根据表格数据可知:
前5天的某型号口罩销售价格p(元/只)和销量q(只)与第x天的关系为:
p=x+1,1≤x≤5且x为整数;
q=5x+65,1≤x≤5且x为整数;
(2)当1≤x≤5且x为整数时,
W=(x+1﹣0.5)(5x+65)
=5x2+x+;
当6≤x≤30且x为整数时,
W=(1﹣0.5)(﹣2x2+80x﹣200)
=﹣x2+40x﹣100.
即有W=,
当1≤x≤5且x为整数时,售价,销量均随x的增大而增大,
故当x=5时,W有最大值为:495元;
当6≤x≤30且x为整数时,
W═﹣x2+40x﹣100=﹣(x﹣20)2+300,
故当x=20时,W有最大值为:300元;
由495>300,可知:
第5天时利润最大为495元.
(3)根据题意可知:
获得的正常利润之外的非法所得部分为:
(2﹣0.5﹣0.5)×70+(3﹣1)×75+(4﹣1)×80+(5﹣1)×85+(6﹣1)×90=1250(元),
∴1250m≥2000,
解得m≥.
则m的取值范围为m≥.
故答案为:m≥.
15.(2020?荆门)2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为p=,销售量y(千克)与x之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
【解答】解:(1)当0<x≤20时,设y与x的函数关系式为y=ax+b,
,
解得,,
即当0<x≤20时,y与x的函数关系式为y=﹣2x+80,
当20<x≤30时,设y与x的函数关系式为y=mx+n,
,
解得,,
即当20<x≤30时,y与x的函数关系式为y=4x﹣40,
由上可得,y与x的函数关系式为y=;
(2)设当月第x天的销售额为w元,
当0<x≤20时,w=(x+4)×(﹣2x+80)=(x﹣15)2+500,
∴当x=15时,w取得最大值,此时w=500,
当20<x≤30时,w=(x+12)×(4x﹣40)=(x﹣35)2+500,
∴当x=30时,w取得最大值,此时w=480,
由上可得,当x=15时,w取得最大值,此时w=500,
答:当月第15天,该农产品的销售额最大,最大销售额是500元.
16.(2019秋?宁明县期中)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.求S与x之间的函数表达式,并求自变量x的取值范围.
【解答】解:∵AB=xm,∴BC=(28﹣x)m,
S=AB?BC=x(28﹣x)=﹣x2+28x,
∵篱笆的长为28m,∴0<x<28,
即S=﹣x2+28x(0<x<28).
17.(2020?湖州模拟)如图,已知在平面直角坐标系xOy中,直线y=x+b经过点B(1,3),且与直线y=﹣2x交于点A,抛物线y=(x﹣m)2+n的顶点在直线y=﹣2x上运动.
(1)求点A的坐标.
(2)当抛物线经过点A时,求抛物线的解析式.
(3)当﹣1<x<1时,始终满足(x﹣m)2+n<x+b,结合图象,直接写出m的取值范围.
【解答】解:(1)将点B的坐标代入y=x+b得:+b=3,解得:b=2.5,
故y=x+,
联立,解得,
故点A的坐标为(﹣1,2);
(2)∵抛物线y=(x﹣m)2+n的顶点在直线y=﹣2x上运动,则n=﹣2m,
则y=(x﹣m)2﹣2m,
将点A的坐标代入上式并解得:m=±1,
故抛物线的表达式为:y=(x﹣1)2﹣2或y=(x+1)2+2;
(3)设:y=(x﹣m)2﹣2m,y′=x+,
当﹣1<x<1时,始终满足(x﹣m)2+n<x+b,即y在y′的下方,
当x=﹣1时,y′=×(﹣1)+=2,而y=(﹣1﹣m)2﹣2m=m2+1,
即m2+1<2,解得:﹣1<m<1;
当x=1时,同理可得:y′=3,y=m2﹣4m+1,
即y=m2﹣4m+1<3,解得2﹣<m<2+;
故m的取值范围为2﹣<m<1.
18.(2020?宁波模拟)如图,抛物线y1=﹣x2﹣x+c与直线y2=x+b交于A,B(1,0)两点.
(1)分别求c,b的值.
(2)求y1﹣y2的最大值.
(3)求点A的坐标,并根据图象判断,当x取何值时,y1>y2?
【解答】解:(1)∵抛物线y1=﹣x2﹣x+c与直线y2=x+b交于A,B(1,0)两点,
∴0=﹣1﹣1+c,0=×1+b,
解得,b=﹣,c=2;
(2)∵b=﹣,c=2,
∴抛物线y1=﹣x2﹣x+2,直线y2=x﹣,
∴y1﹣y2
=(﹣x2﹣x+2)﹣(x﹣)
=﹣x2﹣x+
=﹣(x+)2+,
即当x=﹣时,y1﹣y2取得最大值,
即y1﹣y2的最大值是;
(3),
解得,或,
∴点A的坐标为(﹣,﹣),
由图象可得,
当﹣<x<1时,y1>y2.
19.(2020?镇海区模拟)如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
【解答】解:(1)∵直线y=x+m经过点A(0,3),
∴m=3,
∴直线为y=x+3,
∵二次函数y=ax2+2x+c的图象经过点A(0,3),且对称轴为直线x=1.
∴,解得,
∴二次函数解析式为y=﹣x2+2x+3;
(2)解得或,
∴B(1,4),
∴△OAB的面积==;
(3)由图象可知:当x<0或x>1时,该一次函数值大于二次函数值.
20.(2020?雅安)已知二次函数y=x2+bx+c(a≠0)的图象与x轴的交于A、B(1,0)两点,与y轴交于点C(0,﹣3),
(1)求二次函数的表达式及A点坐标;
(2)D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标;
(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N.使以M、N、B、O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).
【解答】解:(1)把B(1,0),C(0,﹣3)代入y=x2+bx+c
则有,
解得
∴二次函数的解析式为y=x2+2x﹣3,
令y=0,得到x2+2x﹣3=0,解得x=﹣3或1,
∴A(﹣3,0).
(2)如图1中连接AD,CD.
∵点D到直线AC的距离取得最大,
∴此时△DAC的面积最大
设直线AC解析式为:y=kx+b,
∵A(﹣3,0),C(0,﹣3),
∴,
解得,,
∴直线AC的解析式为y=﹣x﹣3,
过点D作x轴的垂线交AC于点G,设点D的坐标为(x,x2+2x﹣3),
则G(x,﹣x﹣3),
∵点D在第三象限,
∴DG=﹣x﹣3﹣(x2+2x﹣3)=﹣x﹣3﹣x2﹣2x+3=﹣x2﹣3x,
∴S△ACD=?DG?OA=(﹣x2﹣3x)×3=﹣x2﹣=﹣(x+)2+,
∴当x=﹣时,S最大=,点D(﹣,﹣),
∴点D到直线AC的距离取得最大时,D(﹣,﹣).
(3)如图2中,当OB是平行四边形的边时,OB=MN=1,OB∥MN,可得N(﹣2,﹣3)或N′(0,﹣3),
当OB为对角线时,点N″的横坐标为2,
x=2时,y=4+4﹣3=5,
∴N″(2,5).
综上所述,满足条件的点N的坐标为(﹣2,﹣3)或(0,﹣3)或(2,5).
21.(2020?丹东)如图1,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,A点坐标为(﹣2,0),与y轴交于点C(0,4),直线y=﹣x+m与抛物线交于B,D两点.
(1)求抛物线的函数表达式.
(2)求m的值和D点坐标.
(3)点P是直线BD上方抛物线上的动点,过点P作x轴的垂线,垂足为H,交直线BD于点F,过点D作x轴的平行线,交PH于点N,当N是线段PF的三等分点时,求P点坐标.
(4)如图2,Q是x轴上一点,其坐标为(﹣,0).动点M从A出发,沿x轴正方向以每秒5个单位的速度运动,设M的运动时间为t(t>0),连接AD,过M作MG⊥AD于点G,以MG所在直线为对称轴,线段AQ经轴对称变换后的图形为A′Q′,点M在运动过程中,线段A′Q′的位置也随之变化,请直接写出运动过程中线段A′Q′与抛物线有公共点时t的取值范围.
【解答】解:(1)把A(﹣2,0),C(0,4)代入y=﹣12x2+bx+c,
得到,
解得,
∴抛物线的解析式为y=﹣x2+x+4.
(2)令y=0,则有﹣x2+x+4=0,
解得x=﹣2或4,
∴B(4,0),
把B(4,0)代入y=﹣x+m,得到m=2,
∴直线BD的解析式为y=﹣x+2,
由,解得或,
∴D(﹣1,).
(3)设P(a,﹣a2+a+4),
则N(a,),F(a,﹣a+2),
∴PN=﹣a2+a+4﹣=﹣a2+a+,NF=﹣(﹣a+2)=a+,
∵N是线段PF的三等分点,
∴PN=2NF或NF=2PN,
∴﹣a2+a+=a+1或a+=﹣a2+2a+3,
解得a=±1或﹣1或,
∵a>0,
∴a=1或,
∴P(1,)或(,).
(4)如图2中,
∵A(﹣2,0),D(﹣1,),
∴直线AD的解析式为y=x+5,
∵A′Q′与AQ关于MG对称,MG⊥AD,
∴QQ′∥AD,
∵Q(﹣,0),
∴直线QQ′的解析式为y=x+2,设直线QQ′交抛物线于E,
由,解得或,
∴E(1,),
当点A′与D重合时,直线GM的解析式为y=﹣x+,可得M(1,0),此时t=,
当点Q′与E重合时,直线GM经过点(,),
∵GM⊥AD,
∴GM的解析式为y=﹣x+,
令y=0,可得x=,
∴M(,0),此时t==,
观察图象可知,满足条件的t的值为≤t≤.
22.(2020?永州)在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在y轴上,另两个顶点A,B在x轴上,且AB=4,抛物线经过A,B,C三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知Q(1,﹣)是抛物线上一定点,问抛物线上是否存在点P,使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.
【解答】解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
在等腰Rt△ABC中,OC垂直平分AB,且AB=4,
∴OA=OB=OC=2,
∴A(﹣2,0),B(2,0),C(0,﹣2),
∴,
解得,,
∴抛物线的解析式为y=﹣2;
(2)①设直线l的解析式为y=kx,M(x1,y1),N(x2,y2),
由,可得,
∴x1+x2=2k,x1?x2=﹣4,
∴,
∴,
∴,
∴当k=0时2取最小值为4.
∴△CMN面积的最小值为4.
②假设抛物线上存在点P(m,﹣2),使得点P与点Q关于直线l对称,
∴OP=OQ,即,
解得,,,m3=1,m4=﹣1,
∵m3=1,m4=﹣1不合题意,舍去,
当时,点P(),
线段PQ的中点为(),
∴,
∴,
∴直线l的表达式为:y=(1﹣)x,
当时,点P(﹣,﹣),
线段PQ的中点为(,﹣1),
∴,
∴,
∴直线l的解析式为y=(1+)x.
综上,直线l的解析式为y=(1﹣)x或y=(1+)x.
23.(2020?鄂尔多斯)如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数解析式;
(2)点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;
(3)如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.
【解答】解:(1)∵抛物线y=x2+bx+c交x轴于点A(1,0),与y轴交于点C(0,﹣3),
∴,
解得:,
∴抛物线解析式为:y=x2+2x﹣3;
(2)∵抛物线y=x2+2x﹣3与x轴于A,B两点,
∴点B(﹣3,0),
∵点B(﹣3,0),点C(0,﹣3),
∴OB=OC=3,
∴∠OBC=∠OCB=45°,
如图1,当点D在点C上方时,
∵∠DBC=15°,
∴∠OBD=30°,
∴tan∠DBO==,
∴OD=×3=,
∴CD=3﹣;
若点D在点C下方时,
∵∠DBC=15°,
∴∠OBD=60°,
∴tan∠DBO==,
∴OD=3,
∴DC=3﹣3,
综上所述:线段CD的长度为3﹣或3﹣3;
(3)如图2,在BO上截取OE=OA,连接CE,过点E作EF⊥AC,
∵点A(1,0),点C(0,﹣3),
∴OA=1,OC=3,
∴AC===,
∵OE=OA,∠COE=∠COA=90°,OC=OC,
∴△OCE≌△OCA(SAS),
∴∠ACO=∠ECO,CE=AC=,
∴∠ECA=2∠ACO,
∵∠PAB=2∠ACO,
∴∠PAB=∠ECA,
∵S△AEC=AE×OC=AC×EF,
∴EF==,
∴CF===,
∴tan∠ECA==,
如图2,当点P在AB的下方时,设AO与y轴交于点N,
∵∠PAB=∠ECA,
∴tan∠ECA=tan∠PAB==,
∴ON=,
∴点N(0,),
又∵点A(1,0),
∴直线AP解析式为:y=x﹣,
联立方程组得:,
解得:或,
∴点P坐标为:(﹣,﹣),
当点P在AB的上方时,同理可求直线AP解析式为:y=﹣x+,
联立方程组得:,
解得:或,
∴点P坐标为:(﹣,),
综上所述:点P的坐标为(﹣,),(﹣,﹣).
24.(2020?鄂州)如图,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C.直线y=x﹣2经过B、C两点.
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线BC及x轴分别交于点D、M.PN⊥BC,垂足为N.设M(m,0).
①点P在抛物线上运动,若P、D、M三点中恰有一点是其它两点所连线段的中点(三点重合除外).请直接写出符合条件的m的值;
②当点P在直线BC下方的抛物线上运动时,是否存在一点P,使△PNC与△AOC相似.若存在,求出点P的坐标;若不存在,请说明理由.
【解答】解:(1)针对于直线y=x﹣2,
令x=0,则y=﹣2,
∴C(0,﹣2),
令y=0,则0=x﹣2,
∴x=4,
∴B(4,0),
将点B,C坐标代入抛物线y=x2+bx+c中,得,
∴,
∴抛物线的解析式为y=x2﹣x﹣2;
(2)①∵PM⊥x轴,M(m,0),
∴P(m,m2﹣m﹣2),D(m,m﹣2),
∵P、D、M三点中恰有一点是其它两点所连线段的中点,
∴Ⅰ、当点D是PM的中点时,(0+m2﹣m﹣2)=,
∴m=﹣或m=4(此时点D,M,P三点重合,舍去),
Ⅱ、当点P是DM的中点时,(0+m﹣2)=m2﹣m﹣2,
∴m=1或m=4(此时点D,M,P三点重合,舍去),
Ⅲ、当点M是DP的中点时,(m2﹣m﹣2+m﹣2)=0,
∴m=2或m=4(此时点D,M,P三点重合,舍去),
即满足条件的m的值为﹣或1或2;
②由(1)知,抛物线的解析式为y=x2﹣x﹣2,
令y=0,则0=x2﹣x﹣2,
∴x=﹣1或x=4,
∴点A(﹣1,0),
∴OA=1,
∵B(4,0),C(0,﹣2),
∴OB=4,OC=2,
∴,
∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴∠OAC=∠OCB,∠ACO=∠OBC,
∵△PNC与△AOC相似,
∴Ⅰ、当△PNC∽△AOC,
∴∠PCN=∠ACO,
∴∠PCN=∠OBC,
∴CP∥OB,
∴点P的纵坐标为﹣2,
∴m2﹣m﹣2=﹣2,
∴m=0(舍)或m=3,
∴P(3,﹣2);
Ⅱ、当△PNC∽△COA时,
∴∠PCN=∠CAO,
∴∠OCB=∠PCD,
∵PD∥OC,
∴∠OCB=∠CDP,
∴∠PCD=∠PDC,
∴PC=PD,
由①知,P(m,m2﹣m﹣2),D(m,m﹣2),
∵C(0,﹣2),
∴PD=2m﹣m2,PC==,
∴2m2﹣m=,
∴m=,
∴P(,﹣),
即满足条件的点P的坐标为(3,﹣2)或(,﹣).
25.(2020?恩施州)如图1,抛物线y=﹣x2+bx+c经过点C(6,0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点.
(1)求抛物线的解析式;
(2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90°,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=﹣x2+bx+c只有一个交点时,求点M的坐标.
(3)△MPC在(2)的旋转变换下,若PC=(如图2).
①求证:EA=ED.
②当点E在(1)所求的抛物线上时,求线段CM的长.
【解答】解:(1)∵点C(6,0)在抛物线上,
∴,
得到6b+c=9,
又∵对称轴为x=2,
∴,
解得b=1,
∴c=3,
∴二次函数的解析式为;
(2)当点M在点C的左侧时,如图2﹣1中:
∵抛物线的解析式为,对称轴为x=2,C(6,0)
∴点A(2,0),顶点B(2,4),
∴AB=AC=4,
∴△ABC是等腰直角三角形,
∴∠1=45°;
∵将△MPC逆时针旋转90°得到△MEF,
∴FM=CM,∠2=∠1=45°,
设点M的坐标为(m,0),
∴点F(m,6﹣m),
又∵∠2=45°,
∴直线EF与x轴的夹角为45°,
∴设直线EF的解析式为y=x+b,
把点F(m,6﹣m)代入得:6﹣m=m+b,解得:b=6﹣2m,
直线EF的解析式为y=x+6﹣2m,
∵直线EF与抛物线只有一个交点,
∴,
整理得:,
∴△=b2﹣4ac=0,解得m=,
点M的坐标为(,0).
当点M在点C的右侧时,如下图:
由图可知,直线EF与x轴的夹角仍是45°,因此直线EF与抛物线不可能只有一个交点.
综上,点M的坐标为(,0).
(3)①当点M在点C的左侧时,如下图,过点P作PG⊥x轴于点G,过点E作EH⊥x轴于点H,
∵,由(2)知∠BCA=45°,
∴PG=GC=1,
∴点G(5,0),
设点M的坐标为(m,0),
∵将△MPC逆时针旋转90°得到△MEF,
∴EM=PM,
∵∠HEM+∠EMH=∠GMP+∠EMH=90°,
∴∠HEM=∠GMP,
在△EHM和△MGP中,,
∴△EHM≌△MGP(AAS),
∴EH=MG=5﹣m,HM=PG=1,
∴点H(m﹣1,0),
∴点E的坐标为(m﹣1,5﹣m);
∴EA==,
又∵D为线段BC的中点,B(2,4),C(6,0),
∴点D(4,2),
∴ED==,
∴EA=ED.
当点M在点C的右侧时,如下图:
同理,点E的坐标仍为(m﹣1,5﹣m),因此EA=ED.
②当点E在(1)所求的抛物线上时,
把E(m﹣1,5﹣m)代入,整理得:m2﹣10m+13=0,
解得:m=或m=,
∴CM=或CM=.
26.(2020?青海)如图1(注:与图2完全相同)所示,抛物线y=﹣+bx+c经过B、D两点,与x轴的另一个交点为A,与y轴相交于点C.
(1)求抛物线的解析式.
(2)设抛物线的顶点为M,求四边形ABMC的面积.(请在图1中探索)
(3)设点Q在y轴上,点P在抛物线上.要使以点A、B、P、Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)
【解答】解:(1)把B(3,0)和D(﹣2,﹣)代入抛物线的解析式得,
,
解得,,
∴抛物线的解析式为:;
(2)令x=0,得=,
∴,
令y=0,得=0,
解得,x=﹣1,或x=3,
∴A(﹣1,0),
∵=,
∴M(1,2),
∴S四边形ABMC=S△AOC+S△COM+S△MOB
=
=;
(3)设Q(0,n),
①当AB为平行四边形的边时,有AB∥PQ,AB=PQ,
a).P点在Q点左边时,则P(﹣4,n),
把P(﹣4,n)代入,得
n=,
∴P(﹣4,﹣);
②当AB为平行四边形的边时,有AB∥PQ,AB=PQ,
当P点在Q点右边时,则P(4,n),
把P(4,n)代入,得
n=,
∴P(4,﹣);
③当AB为平行四边形的对角线时,如图2,AB与PQ交于点E,
则E(1,0),
∵PE=QE,
∴P(2,﹣n),
把P(2,﹣n)代入,得
﹣n=,
∴n=﹣,
∴P(2,).
综上,满足条件的P点坐标为:(﹣4,﹣)或(4,﹣)或(2,).
27.(2020?山西)综合与探究
如图,抛物线y=x2﹣x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为(4,﹣3).
(1)请直接写出A,B两点的坐标及直线l的函数表达式;
(2)若点P是抛物线上的点,点P的横坐标为m(m≥0),过点P作PM⊥x轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标;
(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.
【解答】解:(1)令y=0,得y=x2﹣x﹣3=0,
解得,x=﹣2,或x=6,
∴A(﹣2,0),B(6,0),
设直线l的解析式为y=kx+b(k≠0),则
,
解得,,
∴直线l的解析式为;
(2)如图1,根据题意可知,点P与点N的坐标分别为
P(m,m2﹣m﹣3),N(m,m﹣1),
∴PM=﹣m2+m+3,MN=m+1,NP=﹣m2+m+2,
分两种情况:
①当PM=3MN时,得﹣m2+m+3=3(m+1),
解得,m=0,或m=﹣2(舍),
∴P(0,﹣3);
②当PM=3NP时,得﹣m2+m+3=3(﹣m2+m+2),
解得,m=3,或m=﹣2(舍),
∴P(3,﹣);
∴当点N是线段PM的三等分点时,点P的坐标为(3,﹣)或(0,﹣3);
(3)∵直线l:与y轴于点E,
∴点E的坐标为(0,﹣1),
分再种情况:①如图2,当点Q在y轴的正半轴上时,记为点Q1,
过Q1作Q1H⊥AD于点H,则∠Q1HE=∠AOE=90°,
∵∠Q1EH=∠AEO,
∴△Q1EH∽△AEO,
∴,即
∴Q1H=2HE,
∵∠Q1DH=45°,∠Q1HD=90°,
∴Q1H=DH,
∴DH=2EH,
∴HE=ED,
连接CD,
∵C(0,﹣3),D(4,﹣3),
∴CD⊥y轴,
∴ED=,
∴,,
∴,
∴Q1O=Q1E﹣OE=9,
∴Q1(0,9);
②如图3,当点Q在y轴的负半轴上时,记为点Q2,过Q2作Q2G⊥AD于G,则∠Q2GE=∠AOE=90°,
∵∠Q2EG=∠AEO,
∴△Q2GE∽△AOE,
∴,即,
∴Q2G=2EG,
∵∠Q2DG=45°,∠Q2GD=90°,
∴∠DQ2G=∠Q2DG=45°,
∴DG=Q2G=2EG,
∴ED=EG+DG=3EG,
由①可知,ED=2,
∴3EG=2,
∴,
∴,
∴,
∴,
,
综上,点Q的坐标为(0,9)或(0,﹣).
28.(2020?淄博)如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx+(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是?OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
【解答】解:(1)OA=2=BC,故函数的对称轴为x=1,则x=﹣=1①,
将点A的坐标代入抛物线表达式得:0=4a﹣2b+②,
联立①②并解得,
故抛物线的表达式为:y=﹣x2+x+③;
(2)∵y=﹣x2+x+=﹣(x﹣1)2+3,
∴抛物线的顶点M(1,3)
令y=0,可得x=﹣2或4,
∴点D(4,0);
∵△ADR的面积是?OABC的面积的,
∴×AD×|yR|=×OA×OB,则×6×|yR|=×2×,解得:yR=±④,
联立④③并解得或,
故点R的坐标为(1+,﹣)或(1,﹣)或(1,)或(1﹣,);
(3)①当点P与M重合时,存在唯一的点Q(4,0)与D重合,此时符合题意,P(1,3).
②根据对称性可知.P(1,﹣3),Q与D重合时,也符合题意.
③当点P是EM的中点,点Q是DM的中点时,也符合题意,此时P(1,)
综上所述,满足条件的点P的坐标为(1,3)或(1,﹣3)或(1,).
29.(2020?青岛)某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
(1)按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k≠0)表示.求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2.已知GM=2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)
(3)根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
【解答】解:(1)∵长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m.
∴OH=AB=3,
∴EO=EH﹣OH=4﹣3=1,
∴E(0,1),D(2,0),
∴该抛物线的函数表达式为:y=kx2+1,
把点D(2,0)代入,得k=﹣,
∴该抛物线的函数表达式为:y=﹣x2+1;
(2)∵GM=2,
∴OM=OG=1,
∴当x=1时,y=,
∴N(1,),
∴MN=,
∴S矩形MNFG=MN?GM=×2=,
∴每个B型活动板房的成本是:
425+×50=500(元).
答:每个B型活动板房的成本是500元;
(3)根据题意,得
w=(n﹣500)[100+]
=﹣2(n﹣600)2+20000,
∵每月最多能生产160个B型活动板房,
∴100+≤160,
解得n≥620,
∵﹣2<0,
∴n≥620时,w随n的增大而减小,
∴当n=620时,w有最大值为19200元.
答:公司将销售单价n(元)定为620元时,每月销售B型活动板房所获利润w(元)最大,最大利润是19200元.
30.(2020?咸宁)如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n<)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
【解答】解:(1)直线y=﹣x+2与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为(4,0)、(0,2),
将点B、C的坐标代入抛物线表达式得,解得,
故抛物线的表达式为:y=﹣x2+x+2①;
(2)如图1,作点B关于x轴的对称点B′(0,﹣2),连接AB′交抛物线于点P(P′),则∠PAO=∠BAO,
设直线AB'的解析式为y=kx+m,
∴,
∴,
直线AB′的表达式为:y=x﹣2②,
联立①②并解得:x=3或﹣2,
故点P的坐标为(3,﹣)或(﹣2,﹣3),
当点P与B,C重合时,也满足条件,此时P(0,2)或(,),
综上所述,满足条件的点P的坐标为(3,﹣)或(﹣2,﹣3)或(0,2)或(,).
(3)①过点C作CH⊥x轴于点H,
∵∠MNC=90°,
∴∠MNO+∠CNH=90°,
又∵∠CNH+∠NCH=90°,
∴∠MNO=∠NCH,
∴tan∠MNO=tan∠NCH,即,即,
解得:m=﹣n2+n;
②m=﹣n2+n,
∵<0,故m有最大值,当n=时,m的最大值为,
而m>0,
故0<m<时,符合条件的N点的个数有2个.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
