4.3 坐标平面内图形的轴对称和平移同步练习(含解析)
文档属性
| 名称 | 4.3 坐标平面内图形的轴对称和平移同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 22:21:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册4.3 坐标平面内图形的轴对称和平移 同步练习
一、单选题
1.在平面直角坐标系中,将点 向下平移3个单位长度,所得点的坐标是(? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
2.在平面直角坐标系中,点 关于x轴对称的点是(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.已知点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2),则点A的变换是(? )
A.?先向左平移1个单位,再向上平移2个单位???????????B.?先向右平移1个单位,再向下平移2个单位
C.?先向左平移1个单位,再向下平移2个单位???????????D.?先向右平移1个单位,再向上平移2个单位
4.已知点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则A(a,b)关于x轴对称的点的坐标为(?? )
A.?(1,﹣5)??????????????????????B.?(1,5)??????????????????????C.?(﹣1,5)??????????????????????D.?(﹣1,﹣5)
5.线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为(??? )
A.?(4,2)????????????????????????????B.?(-4,2)????????????????????????????C.?(-4,-2)????????????????????????????D.?(4,-2)
6.如图,在平面直角坐标系中,点A,B,C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),则点A1 , C1的坐标分别是(??? )
A.?A1(4,4),C1(3,2)??????????????????????????????????B.?A1(3,3),C1(2,1)
C.?A1(4,3),C1(2,3)??????????????????????????????????D.?A1(3,4),C1(2,2)
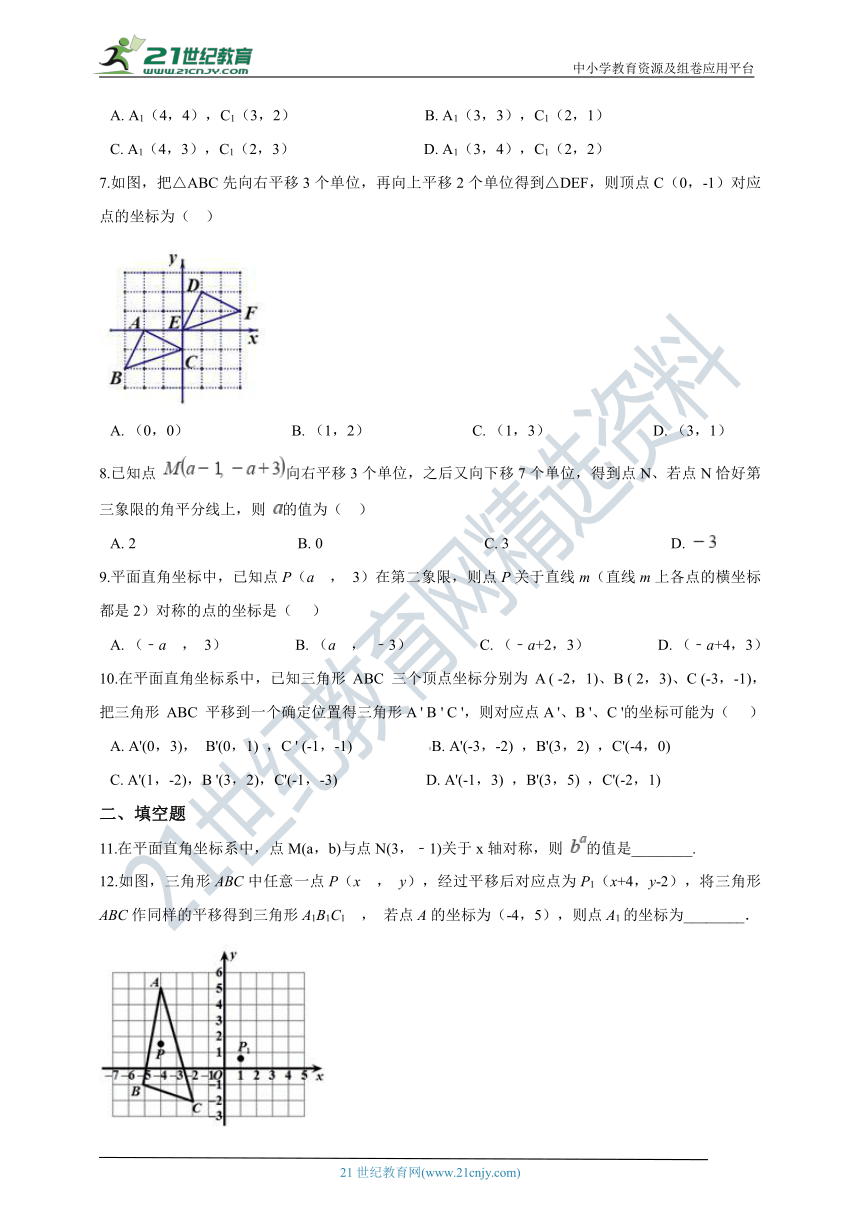
7.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为(?? )
A.?(0,0)???????????????????????????B.?(1,2)???????????????????????????C.?(1,3)???????????????????????????D.?(3,1)
8.已知点 向右平移3个单位,之后又向下移7个单位,得到点N、若点N恰好第三象限的角平分线上,则 的值为(?? )
A.?2??????????????????????????????????????????B.?0??????????????????????????????????????????C.?3??????????????????????????????????????????D.?
9.平面直角坐标中,已知点P(a , 3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( ???)
A.?(﹣a , 3)??????????????????B.?(a , ﹣3)??????????????????C.?(﹣a+2,3)??????????????????D.?(﹣a+4,3)
10.在平面直角坐标系中,已知三角形 ABC 三个顶点坐标分别为 A ( -2,1)、B ( 2,3)、C (-3,-1),把三角形 ABC 平移到一个确定位置得三角形A ' B ' C ',则对应点A '、B '、C '的坐标可能为(??? )
A.?A'(0,3), B'(0,1) ,C ' (-1,-1)????????????????????B.?A'(-3,-2) ,B'(3,2) ,C'(-4,0)
C.?A'(1,-2),B '(3,2),C'(-1,-3) ?????????????????????D.?A'(-1,3) ,B'(3,5) ,C'(-2,1)
二、填空题
11.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则 的值是________.
12.如图,三角形ABC中任意一点P(x , y),经过平移后对应点为P1(x+4,y-2),将三角形ABC作同样的平移得到三角形A1B1C1 , 若点A的坐标为(-4,5),则点A1的坐标为________.
13.小华将平面直角坐标系中的小船图案向上平移了2个单位,又向左平移了3个单位,平移前小船船头A点的坐标为(1,-1),则平移后小船船头A点坐标为________.
14.如图,在直角坐标系xOy中,直线l过点(0,1)且与x轴平行,△ABC关于直线l对称,已知点A坐标是(4,4),则点B的坐标是?________.
?
15.如图,把图1中的圆A经过平移得到圆O(如图2),如果图1⊙A上一点P的坐标为(m,n),那么平移后在图2中的对应点P′的坐标为________
16.若x2+bx+c=(x+5)(x-3),其中b , c为常数,则点P(b , c)关于y轴对称的点的坐标是________.
三、解答题
17.如图,平面直角坐标系中,三角形 的顶点都在网格点上,平移三角形 ,使点 与坐标原点 重合,请写出图中点 的坐标并画出平移后的三角形
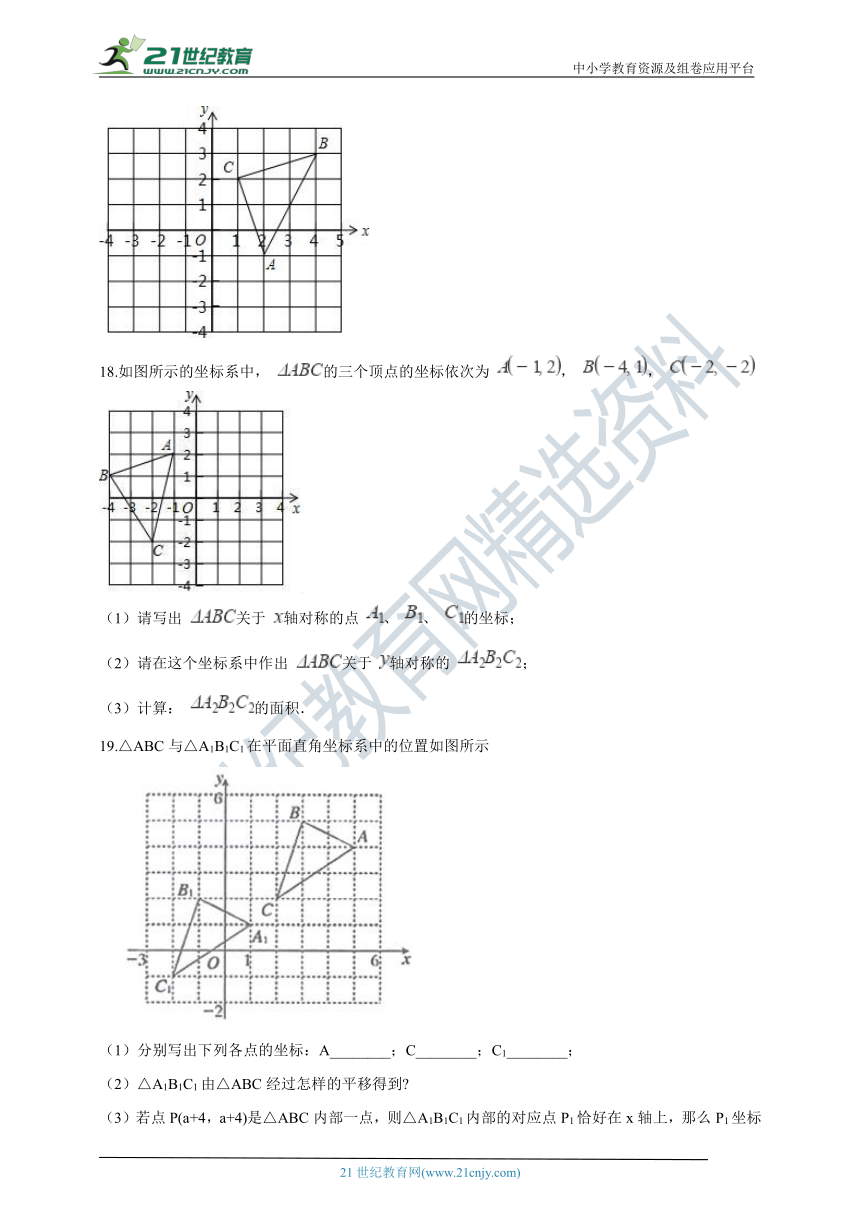
18.如图所示的坐标系中, 的三个顶点的坐标依次为 , ,
(1)请写出 关于 轴对称的点 、 、 的坐标;
(2)请在这个坐标系中作出 关于 轴对称的 ;
(3)计算: 的面积.
19.△ABC与△A1B1C1在平面直角坐标系中的位置如图所示
(1)分别写出下列各点的坐标:A________;C________;C1________;
(2)△A1B1C1由△ABC经过怎样的平移得到?
(3)若点P(a+4,a+4)是△ABC内部一点,则△A1B1C1内部的对应点P1恰好在x轴上,那么P1坐标为________;
(4)求△ABC面积。
答案解析部分
一、单选题
1. D
考点:点的坐标,用坐标表示平移
解:点的平移规律为上加下减,左减右加,可得横坐标不变,纵坐标减3,1-3=-2,
故答案为D.
分析:根据点的平移规律为上加下减,左减右加即可求解.
2. A
考点:关于坐标轴对称的点的坐标特征
解:点 关于x轴对称的点的坐标是 ,
故答案为:A
分析:根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数'解答即可.
3. A
考点:坐标与图形变化﹣平移
解:?∵点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2) ,
∴点A先向左平移1个单位,再向上平移两个单位.
故答案为:A.
分析:点坐标的平移规律:左减右加,变横坐标,上加下减,变纵坐标,据此解答即可.
4. B
考点:关于坐标轴对称的点的坐标特征
解:∵P(﹣1﹣2a,5)关于x轴的对称点的坐标是(﹣1﹣2a,﹣5),
Q(3,b)关于y轴的对称点的坐标是(﹣3,b);
又∵ 点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同 ,
∴﹣1﹣2a=﹣3,b=﹣5;
∴a=1,
∴点A的坐标是(1,﹣5);
∴A点关于x轴对称的点的坐标为(1,5).
故答案为:B.
分析:根据关于x,y轴对称点坐标的特征,分别求出P(﹣1﹣2a,5)关于x轴的对称点的坐标是(﹣1﹣2a,﹣5),Q(3,b)关于y轴的对称点的坐标是(﹣3,b),从而可得﹣1﹣2a=﹣3,b=﹣5,求出a的值,即得点A坐标,从而求出A(a,b)关于x轴对称的点的坐标即可.
5. D
考点:坐标与图形变化﹣对称
解:点M(-4,-2)关于y轴对称的点M1的坐标是(4,-2).
故答案为:D.
分析:关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数.
6. A
考点:坐标与图形变化﹣平移
解:由点B(-4,1)的对应点B1的坐标是(1,2)知,需将△ABC向右移5个单位、上移1个单位,则点A(-1,3)的对应点A1的坐标为(4,4)、点C(-2,1)的对应点C1的坐标为(3,2),
故答案为:A.
分析:根据点B(-4,1)的对应点B1的坐标是(1,2)知,需将△ABC向右移5个单位、上移1个单位,据此根据平移的定义和性质解答可得.
7. D
考点:坐标与图形变化﹣平移
解:∵把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,顶点C(0,﹣1),
∴C(0+3,﹣1+2),
即C(3,1),
故答案为:D.
分析:利用平移规律进而得出答案.
8. D
考点:坐标与图形变化﹣平移
解: 点 向右平移3个单位,之后又向下移7个单位,得到点 ,
点 的横坐标为 ;
纵坐标为 ;
点 恰在第三象限的角平分线上,
;
故答案为:D.
分析:让点M的横坐标加3,纵坐标减7得到点N的坐标,让点N的横纵坐标相等即可求得a的值.
9. D
考点:坐标与图形变化﹣对称
解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a , 3)在第二象限,
∴a到2的距离为:2﹣a ,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a ,
故P点对称的点的坐标是:(﹣a+4,3).
故答案为D .
分析:根据直线m上各点的横坐标都是2,可得其解析式;然后再利用对称点的性质即可解答.
10. D
考点:坐标与图形变化﹣平移
解:A、由A ( -2,1)向右平移2个单位,再向上平移2个单位得到A ' (0,3),而由B ( 2,3)向左平移2个单位,再向下平移2个单位得到B ' (0,1),故此选项不符合题意;
B、由A ( -2,1)向左平移1个单位,再向下平移3个单位得到A ' (-3,-2),而由B ( 2,3)向右平移1个单位,再向下平移1个单位得到B ' (3,2),故此选项不符合题意;
C、由A ( -2,1)向右平移3个单位,再向下平移3个单位得到A ' (1, -2),而由B ( 2,3)向右平移1个单位,再向下平移1个单位得到B ' (3, 2),故此选项不符合题意;
D、将三角形ABC先向右平移1个单位,再向上平移2个单位能得到三角形三角形A ' B ' C ',故此选项符合题意;
故答案为:D.
分析:根据点的坐标找出横纵坐标的变化规律即可.
二、填空题
11. 1
考点:关于坐标轴对称的点的坐标特征
解:在直角坐标系中,关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
∴ =1,
故答案为:1.
分析:根据关于x轴对称的两点的横坐标相同,纵坐标互为相反数求得a、b的值,进而根据有理数的乘方运算法则即可求得答案.
12. (0,3)
考点:点的坐标,坐标与图形变化﹣平移
解:∵三角形ABC中任意一点P(x,y),经过平移后对应点为P1(x+4,y-2),
∴点A的坐标为(?4,5),则点A1的坐标为:(?4+4,5?2)整理得:(0,3).
故答案为:(0,3).
分析:直接利用P点平移规律,进而得出A点平移规律.
13. (-2,1)
考点:用坐标表示平移
解:∵小船图案向上平移了2个单位,又向左平移了3个单位,平移前小船船头A点的坐标为(1,-1),
∴平移后小船船头A点坐标(1-3,-1+2)即(-2,1).
故答案为:(-2,1).
分析:利用平面直角坐标系中点的平移规律:上加下减(纵坐标),左减右加(横坐标),可得到平移后的点A的坐标。
14. (4,﹣2)
考点:坐标与图形变化﹣对称
解:根据题意得出点A和点B是关于直线y=1对称的对应点,它们到y=1的距离相等是3个单位长度,
所以点B的坐标是(4,﹣2).
故答案为:(4,﹣2).
分析:根据轴对称的两点到对称轴的距离相等,即可得出答案.
15. (m+2,n-1)
考点:坐标与图形变化﹣平移
解:∵⊙A的圆心坐标为(-2,1),平移后到达O(0,0),
∴图形向右平移了2个单位,有向下平移1个单位,
又∵P的坐标为(m,n),
∴对应点P’的坐标为(m+2,n-1),故答案为(m+2,n-1).
分析:首先根据圆心的坐标确定平移的方法:向右平移了2个单位,有向下平移1个单位,然后可确定P的对应点P’的坐标.
16. (-2,-15)
考点:多项式乘多项式,关于坐标轴对称的点的坐标特征
解:∵(x+5)(x?3)=x2+2x?15,
∴b=2,c=?15,
∴点P的坐标为(2,?15),
∴点P(2,?15)关于y轴对称点的坐标是(?2,?15).
故答案为:(?2,?15).
分析:先利用多项式的乘法展开再根据对应项系数相等确定出b、c的值,然后根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答.
三、解答题
17. 解:(1)A(2,-1),B(4,3),C(1,2)(2)三角形A1OC1为所求。
画图注意:在坐标系中画对一个点给一分
要在坐标系中标出A1 , C1 , 不标的扣一分。
考点:坐标与图形变化﹣平移
分析:(1)根据点在坐标系里的位置,写出点的坐标,即可;
(2)由点B平移后与坐标原点O重合,可知,三角形先向左平移4个单位,再向下平移3个单位得到新的三角形.
18. (1)解:如图,点 的坐标为 、 的坐标为 、 的坐标为 ;
(2)解:如图所示, 即为所求;
(3)解: 的面积为
考点:坐标与图形变化﹣对称
分析:(1)关于x轴对称的点的横坐标相等、纵坐标互为相反数,据此可得;(2)分别作出点A、B、C关于y轴的对称点,再顺次连接可得;(3)利用割补法求解可得.
19. (1)(5,4);(2,2);(-2,-1)
(2)解:先向左平移4个单位,再向下平移3个单位
(3)(-1,0)
(4)解: 面积为:
=3.5
考点:点的坐标,三角形的面积,用坐标表示平移
解:(1)根据各点在平面直角坐标系中的位置,得:A(5,4),C(2,2),C1(-2,-1);
(2)由C(2,2)的对应点为C1(-2,-1),得: △ABC先向左平移4个单位,再向下平移3个单位 ;
(3)点P(a+4,a+4)的对应点为P1(a+4-4,a+4-3),
∵P1(a+4-4,a+4-3)在x轴上,
∴a+4-3=0,
解得a=-1,
∴ P1坐标为(-1,0).
分析:(1)根据各点在平面直角坐标系中的位置,直接可以写出点 A,C,C1的坐标;
(2)观察各对应的坐标变化规律,即可求解;
(3)先求出点P的对应点P1的坐标,由P1在x轴上,纵坐标为0,列出方程,求出a的值,即可求出点P1的坐标;
(4)根据△ABC面积等于正方形的面积减去三个三角形的面积,列出算式进行计算,即可求解.
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册4.3 坐标平面内图形的轴对称和平移 同步练习
一、单选题
1.在平面直角坐标系中,将点 向下平移3个单位长度,所得点的坐标是(? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
2.在平面直角坐标系中,点 关于x轴对称的点是(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.已知点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2),则点A的变换是(? )
A.?先向左平移1个单位,再向上平移2个单位???????????B.?先向右平移1个单位,再向下平移2个单位
C.?先向左平移1个单位,再向下平移2个单位???????????D.?先向右平移1个单位,再向上平移2个单位
4.已知点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则A(a,b)关于x轴对称的点的坐标为(?? )
A.?(1,﹣5)??????????????????????B.?(1,5)??????????????????????C.?(﹣1,5)??????????????????????D.?(﹣1,﹣5)
5.线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为(??? )
A.?(4,2)????????????????????????????B.?(-4,2)????????????????????????????C.?(-4,-2)????????????????????????????D.?(4,-2)
6.如图,在平面直角坐标系中,点A,B,C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),则点A1 , C1的坐标分别是(??? )
A.?A1(4,4),C1(3,2)??????????????????????????????????B.?A1(3,3),C1(2,1)
C.?A1(4,3),C1(2,3)??????????????????????????????????D.?A1(3,4),C1(2,2)
7.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为(?? )
A.?(0,0)???????????????????????????B.?(1,2)???????????????????????????C.?(1,3)???????????????????????????D.?(3,1)
8.已知点 向右平移3个单位,之后又向下移7个单位,得到点N、若点N恰好第三象限的角平分线上,则 的值为(?? )
A.?2??????????????????????????????????????????B.?0??????????????????????????????????????????C.?3??????????????????????????????????????????D.?
9.平面直角坐标中,已知点P(a , 3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( ???)
A.?(﹣a , 3)??????????????????B.?(a , ﹣3)??????????????????C.?(﹣a+2,3)??????????????????D.?(﹣a+4,3)
10.在平面直角坐标系中,已知三角形 ABC 三个顶点坐标分别为 A ( -2,1)、B ( 2,3)、C (-3,-1),把三角形 ABC 平移到一个确定位置得三角形A ' B ' C ',则对应点A '、B '、C '的坐标可能为(??? )
A.?A'(0,3), B'(0,1) ,C ' (-1,-1)????????????????????B.?A'(-3,-2) ,B'(3,2) ,C'(-4,0)
C.?A'(1,-2),B '(3,2),C'(-1,-3) ?????????????????????D.?A'(-1,3) ,B'(3,5) ,C'(-2,1)
二、填空题
11.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则 的值是________.
12.如图,三角形ABC中任意一点P(x , y),经过平移后对应点为P1(x+4,y-2),将三角形ABC作同样的平移得到三角形A1B1C1 , 若点A的坐标为(-4,5),则点A1的坐标为________.
13.小华将平面直角坐标系中的小船图案向上平移了2个单位,又向左平移了3个单位,平移前小船船头A点的坐标为(1,-1),则平移后小船船头A点坐标为________.
14.如图,在直角坐标系xOy中,直线l过点(0,1)且与x轴平行,△ABC关于直线l对称,已知点A坐标是(4,4),则点B的坐标是?________.
?
15.如图,把图1中的圆A经过平移得到圆O(如图2),如果图1⊙A上一点P的坐标为(m,n),那么平移后在图2中的对应点P′的坐标为________
16.若x2+bx+c=(x+5)(x-3),其中b , c为常数,则点P(b , c)关于y轴对称的点的坐标是________.
三、解答题
17.如图,平面直角坐标系中,三角形 的顶点都在网格点上,平移三角形 ,使点 与坐标原点 重合,请写出图中点 的坐标并画出平移后的三角形
18.如图所示的坐标系中, 的三个顶点的坐标依次为 , ,
(1)请写出 关于 轴对称的点 、 、 的坐标;
(2)请在这个坐标系中作出 关于 轴对称的 ;
(3)计算: 的面积.
19.△ABC与△A1B1C1在平面直角坐标系中的位置如图所示
(1)分别写出下列各点的坐标:A________;C________;C1________;
(2)△A1B1C1由△ABC经过怎样的平移得到?
(3)若点P(a+4,a+4)是△ABC内部一点,则△A1B1C1内部的对应点P1恰好在x轴上,那么P1坐标为________;
(4)求△ABC面积。
答案解析部分
一、单选题
1. D
考点:点的坐标,用坐标表示平移
解:点的平移规律为上加下减,左减右加,可得横坐标不变,纵坐标减3,1-3=-2,
故答案为D.
分析:根据点的平移规律为上加下减,左减右加即可求解.
2. A
考点:关于坐标轴对称的点的坐标特征
解:点 关于x轴对称的点的坐标是 ,
故答案为:A
分析:根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数'解答即可.
3. A
考点:坐标与图形变化﹣平移
解:?∵点A的坐标为(a,b),若点A经过变换得到点(a-1,b+2) ,
∴点A先向左平移1个单位,再向上平移两个单位.
故答案为:A.
分析:点坐标的平移规律:左减右加,变横坐标,上加下减,变纵坐标,据此解答即可.
4. B
考点:关于坐标轴对称的点的坐标特征
解:∵P(﹣1﹣2a,5)关于x轴的对称点的坐标是(﹣1﹣2a,﹣5),
Q(3,b)关于y轴的对称点的坐标是(﹣3,b);
又∵ 点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同 ,
∴﹣1﹣2a=﹣3,b=﹣5;
∴a=1,
∴点A的坐标是(1,﹣5);
∴A点关于x轴对称的点的坐标为(1,5).
故答案为:B.
分析:根据关于x,y轴对称点坐标的特征,分别求出P(﹣1﹣2a,5)关于x轴的对称点的坐标是(﹣1﹣2a,﹣5),Q(3,b)关于y轴的对称点的坐标是(﹣3,b),从而可得﹣1﹣2a=﹣3,b=﹣5,求出a的值,即得点A坐标,从而求出A(a,b)关于x轴对称的点的坐标即可.
5. D
考点:坐标与图形变化﹣对称
解:点M(-4,-2)关于y轴对称的点M1的坐标是(4,-2).
故答案为:D.
分析:关于y轴对称的点的坐标特征是纵坐标不变,横坐标互为相反数.
6. A
考点:坐标与图形变化﹣平移
解:由点B(-4,1)的对应点B1的坐标是(1,2)知,需将△ABC向右移5个单位、上移1个单位,则点A(-1,3)的对应点A1的坐标为(4,4)、点C(-2,1)的对应点C1的坐标为(3,2),
故答案为:A.
分析:根据点B(-4,1)的对应点B1的坐标是(1,2)知,需将△ABC向右移5个单位、上移1个单位,据此根据平移的定义和性质解答可得.
7. D
考点:坐标与图形变化﹣平移
解:∵把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,顶点C(0,﹣1),
∴C(0+3,﹣1+2),
即C(3,1),
故答案为:D.
分析:利用平移规律进而得出答案.
8. D
考点:坐标与图形变化﹣平移
解: 点 向右平移3个单位,之后又向下移7个单位,得到点 ,
点 的横坐标为 ;
纵坐标为 ;
点 恰在第三象限的角平分线上,
;
故答案为:D.
分析:让点M的横坐标加3,纵坐标减7得到点N的坐标,让点N的横纵坐标相等即可求得a的值.
9. D
考点:坐标与图形变化﹣对称
解:∵直线m上各点的横坐标都是2,
∴直线为:x=2,
∵点P(a , 3)在第二象限,
∴a到2的距离为:2﹣a ,
∴点P关于直线m对称的点的横坐标是:2﹣a+2=4﹣a ,
故P点对称的点的坐标是:(﹣a+4,3).
故答案为D .
分析:根据直线m上各点的横坐标都是2,可得其解析式;然后再利用对称点的性质即可解答.
10. D
考点:坐标与图形变化﹣平移
解:A、由A ( -2,1)向右平移2个单位,再向上平移2个单位得到A ' (0,3),而由B ( 2,3)向左平移2个单位,再向下平移2个单位得到B ' (0,1),故此选项不符合题意;
B、由A ( -2,1)向左平移1个单位,再向下平移3个单位得到A ' (-3,-2),而由B ( 2,3)向右平移1个单位,再向下平移1个单位得到B ' (3,2),故此选项不符合题意;
C、由A ( -2,1)向右平移3个单位,再向下平移3个单位得到A ' (1, -2),而由B ( 2,3)向右平移1个单位,再向下平移1个单位得到B ' (3, 2),故此选项不符合题意;
D、将三角形ABC先向右平移1个单位,再向上平移2个单位能得到三角形三角形A ' B ' C ',故此选项符合题意;
故答案为:D.
分析:根据点的坐标找出横纵坐标的变化规律即可.
二、填空题
11. 1
考点:关于坐标轴对称的点的坐标特征
解:在直角坐标系中,关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
∴ =1,
故答案为:1.
分析:根据关于x轴对称的两点的横坐标相同,纵坐标互为相反数求得a、b的值,进而根据有理数的乘方运算法则即可求得答案.
12. (0,3)
考点:点的坐标,坐标与图形变化﹣平移
解:∵三角形ABC中任意一点P(x,y),经过平移后对应点为P1(x+4,y-2),
∴点A的坐标为(?4,5),则点A1的坐标为:(?4+4,5?2)整理得:(0,3).
故答案为:(0,3).
分析:直接利用P点平移规律,进而得出A点平移规律.
13. (-2,1)
考点:用坐标表示平移
解:∵小船图案向上平移了2个单位,又向左平移了3个单位,平移前小船船头A点的坐标为(1,-1),
∴平移后小船船头A点坐标(1-3,-1+2)即(-2,1).
故答案为:(-2,1).
分析:利用平面直角坐标系中点的平移规律:上加下减(纵坐标),左减右加(横坐标),可得到平移后的点A的坐标。
14. (4,﹣2)
考点:坐标与图形变化﹣对称
解:根据题意得出点A和点B是关于直线y=1对称的对应点,它们到y=1的距离相等是3个单位长度,
所以点B的坐标是(4,﹣2).
故答案为:(4,﹣2).
分析:根据轴对称的两点到对称轴的距离相等,即可得出答案.
15. (m+2,n-1)
考点:坐标与图形变化﹣平移
解:∵⊙A的圆心坐标为(-2,1),平移后到达O(0,0),
∴图形向右平移了2个单位,有向下平移1个单位,
又∵P的坐标为(m,n),
∴对应点P’的坐标为(m+2,n-1),故答案为(m+2,n-1).
分析:首先根据圆心的坐标确定平移的方法:向右平移了2个单位,有向下平移1个单位,然后可确定P的对应点P’的坐标.
16. (-2,-15)
考点:多项式乘多项式,关于坐标轴对称的点的坐标特征
解:∵(x+5)(x?3)=x2+2x?15,
∴b=2,c=?15,
∴点P的坐标为(2,?15),
∴点P(2,?15)关于y轴对称点的坐标是(?2,?15).
故答案为:(?2,?15).
分析:先利用多项式的乘法展开再根据对应项系数相等确定出b、c的值,然后根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答.
三、解答题
17. 解:(1)A(2,-1),B(4,3),C(1,2)(2)三角形A1OC1为所求。
画图注意:在坐标系中画对一个点给一分
要在坐标系中标出A1 , C1 , 不标的扣一分。
考点:坐标与图形变化﹣平移
分析:(1)根据点在坐标系里的位置,写出点的坐标,即可;
(2)由点B平移后与坐标原点O重合,可知,三角形先向左平移4个单位,再向下平移3个单位得到新的三角形.
18. (1)解:如图,点 的坐标为 、 的坐标为 、 的坐标为 ;
(2)解:如图所示, 即为所求;
(3)解: 的面积为
考点:坐标与图形变化﹣对称
分析:(1)关于x轴对称的点的横坐标相等、纵坐标互为相反数,据此可得;(2)分别作出点A、B、C关于y轴的对称点,再顺次连接可得;(3)利用割补法求解可得.
19. (1)(5,4);(2,2);(-2,-1)
(2)解:先向左平移4个单位,再向下平移3个单位
(3)(-1,0)
(4)解: 面积为:
=3.5
考点:点的坐标,三角形的面积,用坐标表示平移
解:(1)根据各点在平面直角坐标系中的位置,得:A(5,4),C(2,2),C1(-2,-1);
(2)由C(2,2)的对应点为C1(-2,-1),得: △ABC先向左平移4个单位,再向下平移3个单位 ;
(3)点P(a+4,a+4)的对应点为P1(a+4-4,a+4-3),
∵P1(a+4-4,a+4-3)在x轴上,
∴a+4-3=0,
解得a=-1,
∴ P1坐标为(-1,0).
分析:(1)根据各点在平面直角坐标系中的位置,直接可以写出点 A,C,C1的坐标;
(2)观察各对应的坐标变化规律,即可求解;
(3)先求出点P的对应点P1的坐标,由P1在x轴上,纵坐标为0,列出方程,求出a的值,即可求出点P1的坐标;
(4)根据△ABC面积等于正方形的面积减去三个三角形的面积,列出算式进行计算,即可求解.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
