4.2.2 平面直角坐标系同步练习(含解析)
文档属性
| 名称 | 4.2.2 平面直角坐标系同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 22:19:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册4.2 平面直角坐标系(2)同步练习
一、单选题
1.如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是(??? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
2.如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的 ,则点A的对应点A′的坐标是(??? )
A.?(2,3)?????????????????????????????????B.?(6,1)?????????????????????????????????C.?(2,1)?????????????????????????????????D.?(3,3)
3.如图,在平面直角坐标系中,已知点B,C在x轴上,AB⊥x轴于点B,DA⊥AB.若AD=5,点A的坐标为(-2,7),则点D的坐标为(?? )
A.?(-2,2)?????????????????????????????B.?(-2,12)?????????????????????????????C.?(3,7)?????????????????????????????D.?(-7,7)
4.如图,△ABC顶点C的坐标是(1,-3),过点C作AB边上的高线CD,则垂足D点坐标为( )
A.?(1,0)??????????????????????????B.?(0,1)??????????????????????????C.?(-3,0)??????????????????????????D.?(0,-3)
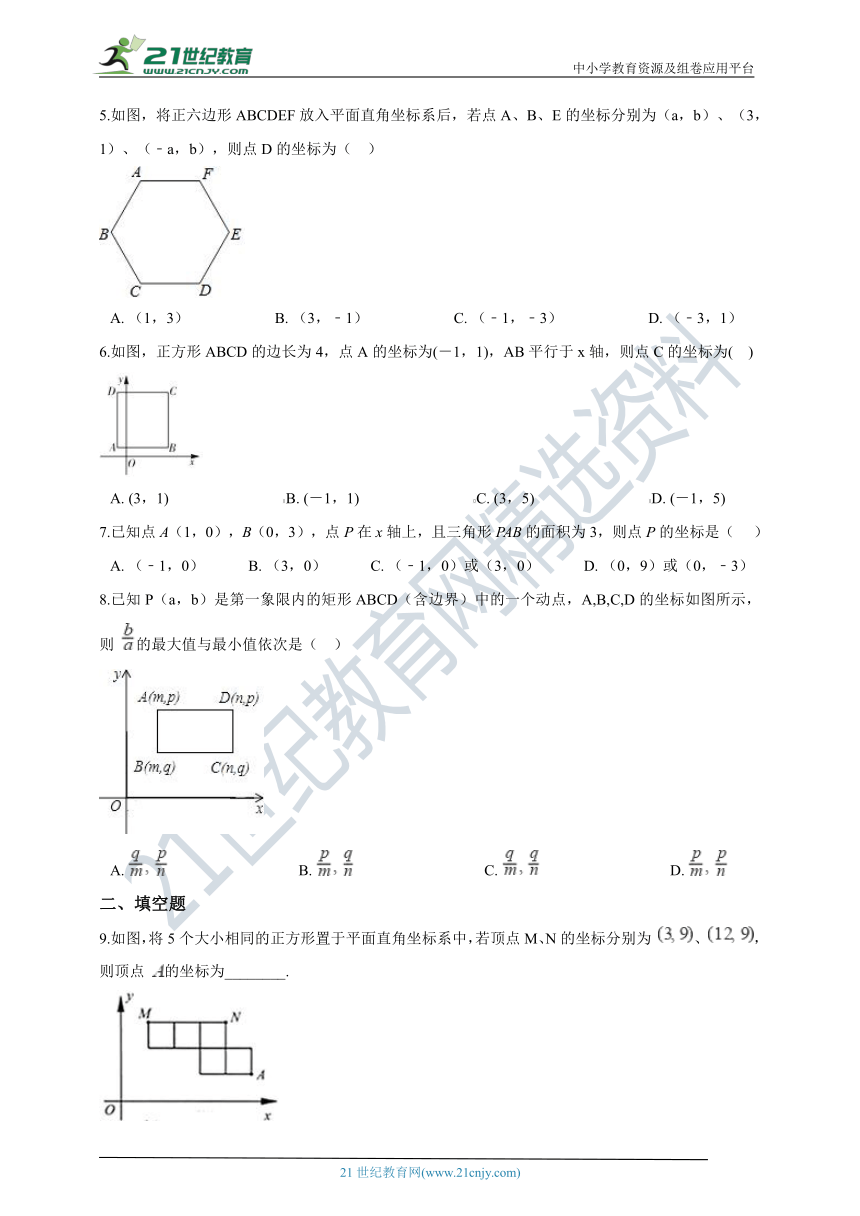
5.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( ??)
A.?(1,3)??????????????????????B.?(3,﹣1)??????????????????????C.?(﹣1,﹣3)??????????????????????D.?(﹣3,1)
6.如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为(?? )
A.?(3,1)??????????????????????????????B.?(-1,1)??????????????????????????????C.?(3,5)??????????????????????????????D.?(-1,5)
7.已知点A(1,0),B(0,3),点P在x轴上,且三角形PAB的面积为3,则点P的坐标是(??? )
A.?(﹣1,0)???????????B.?(3,0)???????????C.?(﹣1,0)或(3,0)???????????D.?(0,9)或(0,﹣3)
8.已知P(a,b)是第一象限内的矩形ABCD(含边界)中的一个动点,A,B,C,D的坐标如图所示,则 的最大值与最小值依次是(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
二、填空题
9.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为________.
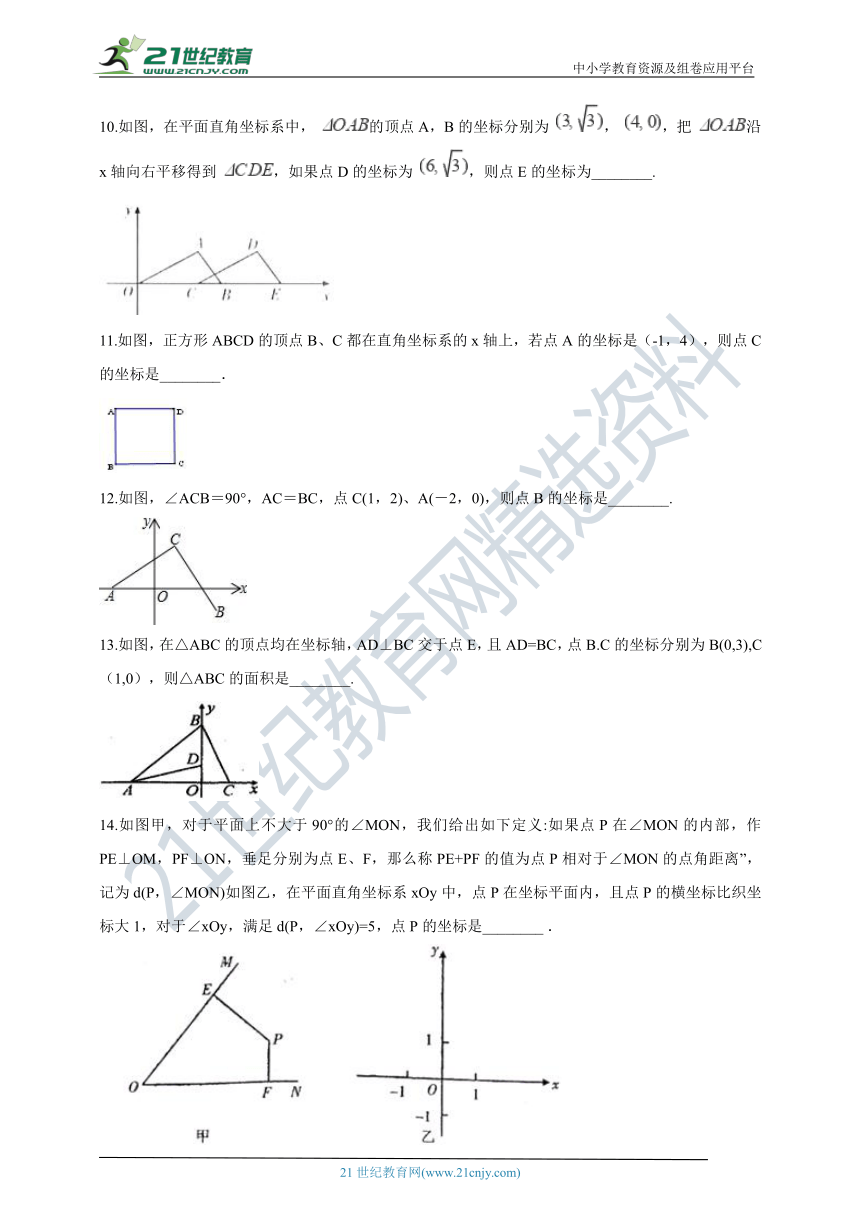
10.如图,在平面直角坐标系中, 的顶点A,B的坐标分别为 , ,把 沿x轴向右平移得到 ,如果点D的坐标为 ,则点E的坐标为________.
11.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是________.
12.如图,∠ACB=90°,AC=BC,点C(1,2)、A(-2,0),则点B的坐标是________.
13.如图,在△ABC的顶点均在坐标轴,AD⊥BC交于点E,且AD=BC,点B.C的坐标分别为B(0,3),C(1,0),则△ABC的面积是________.
14.如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的点角距离”,记为d(P,∠MON)如图乙,在平面直角坐标系xOy中,点P在坐标平面内,且点P的横坐标比织坐标大1,对于∠xOy,满足d(P,∠xOy)=5,点P的坐标是________?.
三、解答题
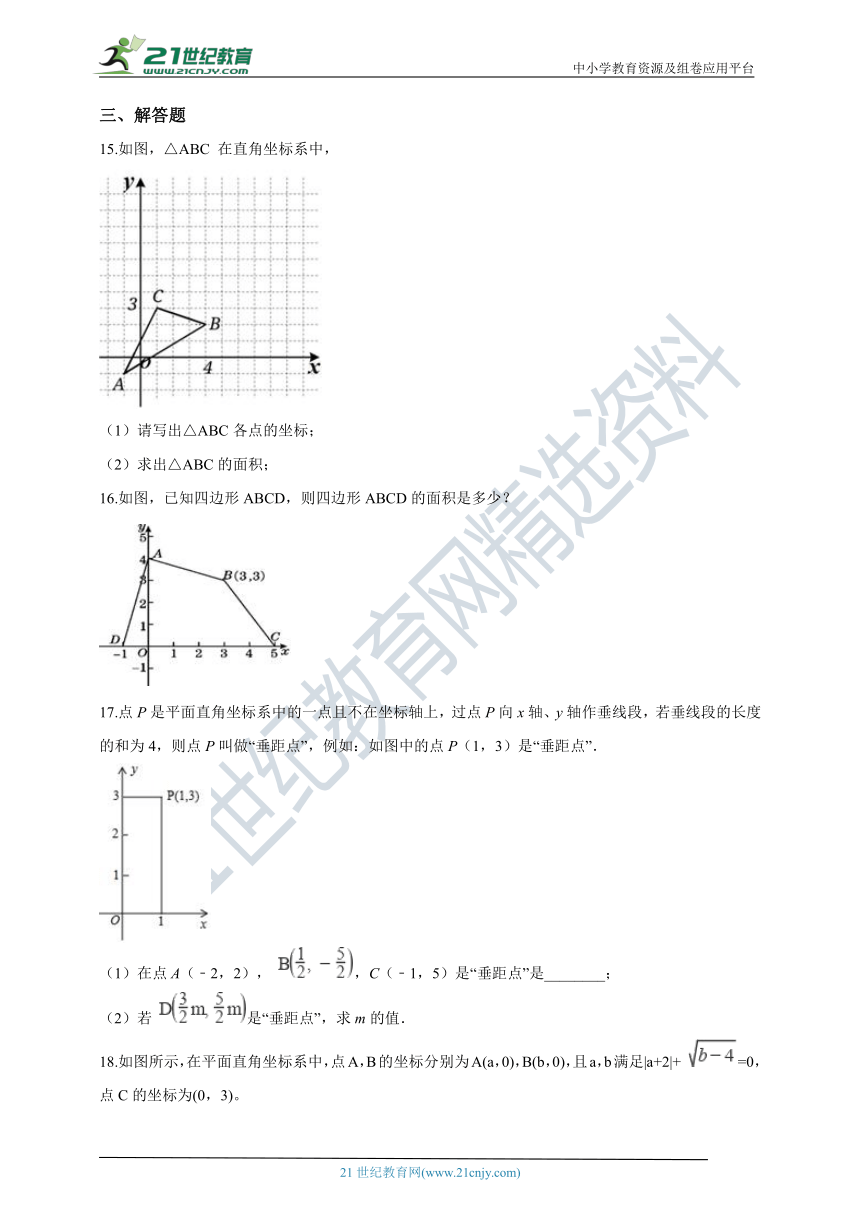
15.如图,△ABC 在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积;
16.如图,已知四边形ABCD,则四边形ABCD的面积是多少?
17.点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
(1)在点A(﹣2,2), ,C(﹣1,5)是“垂距点”是________;
(2)若 是“垂距点”,求m的值.
18.如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+ =0,点C的坐标为(0,3)。
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM= S三角形ABC , 试求点M的坐标。
答案解析部分
一、单选题
1. D
考点:点的坐标,正方形的性质
解:∵O , D两点的坐标分别是 , ,
∴OD=6,
∵四边形 是正方形,
∴OB⊥BC , OB=BC=6
∴C点的坐标为: ,
故答案为:D .
分析:利用O , D两点的坐标,求出OD的长度,利用正方形的性质求出OB , BC的长度,进而得出C点的坐标即可.
2. A
考点:坐标与图形性质
解:点A变化前的坐标为(6,3),
将纵坐标保持不变,横坐标变为原来的 ,
则点A的对应点A′坐标是(2,3).
故答案为:A.
分析:先写出点A的坐标为(6,3),纵坐标保持不变,横坐标变为原来的 ,即可判断出答案.
3. C
考点:坐标与图形性质
解:如图,设AD与y轴的交点为E,
在直角梯形ABCD中,∵点A的坐标为(-2,7),
∴OB=2,OE=7,
∵AD=5,
∴DE=5-2=3,
∴点D的坐标为(3,7).
故答案为:C.
分析:根据图形中点A的坐标和DA⊥AB、AB⊥x轴,得到AD⊥y轴,再由AD=5,得到点D的坐标.
4. A
考点:坐标与图形性质
解:如图,
∵CD⊥x轴,
∴CD∥y轴,
∵点C的坐标是(1,-3),
∴点D的横坐标为1,
∵点D在x轴上,
∴点D的纵坐标为0,
∴点D的坐标为(1,0).
故答案为:A.
分析:根据在同一平面内,垂直于同一直线的两直线平行可得CD∥y轴,再根据平行于y轴上的点的横坐标相同解答.
5.D
考点:坐标与图形性质
解:如图,由点A、E的坐标分别为(a,b)、(﹣a,b)知A、E两点关于y轴对称,
则B、D两点也关于y轴对称,
∵B(3,1),
∴D(﹣3,1),
故选:D.
分析:由A、E两点的纵坐标相等而横坐标互为相反数知A、E两点关于y轴对称,结合图形知B、D两点也关于y轴对称,据此可得答案.
6.C
考点:坐标与图形性质
解:∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,
∴点B的横坐标为:﹣1+4=3,纵坐标为:1,
∴点B的坐标为(3,1),
∴点C的横坐标为:3,纵坐标为:1+4=5,∴点C的坐标为(3,5).
故答案为:C
分析:根据正方形的性质及边长为4,点A的坐标为(﹣1,1),就可得出点C的坐标。
7. C
考点:坐标与图形性质
解:如图,设P(m , 0),
由题意: ?|1﹣m|?3=3,
∴m=﹣1或3,
∴P(﹣1,0)或(3,0),
故答案为:C .
分析:根据题意画出图像,由三角形的面积公式即可求解判断.
8. B
考点:坐标与图形性质
解:如图所示:当 取最大值时:即a最小,b最大,则a=m,b=p,
∴ 的最大值为: ,
当 取最小值时:即a最大,b最小,则a=n,b=q,
∴ 的最小值为: .
故答案为:B
分析:P(a,b)是第一象限内的矩形ABCD(含边界)中的一个动点,要求的最大值,则需要满足a最小,b最大,则a=m,b=p,从而得出答案;要求的最小值,则需要满足a最大,b最小,则a=n,b=q,,根据除法的意义得出答案。
二、填空题
9. (15,3)
考点:坐标与图形性质
解:设正方形的边长为 ,
则由题设条件可知:
解得:
点A的横坐标为: ,点A的纵坐标为:
故点A的坐标为 .
故答案为: .
分析:先根据条件,算出每个正方形的边长,再根据坐标的变换计算出点A的坐标即可.
10. (7,0)
考点:坐标与图形性质
解:由题意知:A、B两点之间的横坐标差为: ,
由平移性质可知:E、D两点横坐标之差与B、A两点横坐标之差相等,
设E点横坐标为a,
则a-6=1,∴a=7,
∴E点坐标为(7,0) .
故答案为:(7,0) .
分析:根据B点横坐标与A点横坐标之差和E点横坐标与D点横坐标之差相等即可求解.
11. (3,0)
考点:坐标与图形性质
解:∵ 正方形ABCD的顶点B、C都在直角坐标系的x轴上,点A的坐标是(-1,4)
∴BC=AB=4,B(-1,0)
∴点C的坐标是(3,0).
分析:根据点A的坐标即可确定正方形的边长及点B的坐标,从而求得点C的坐标.
12. (3,-1)
考点:坐标与图形性质
解:过C和B分别作CD⊥OD于D,BE⊥CD于E,
∵∠ACB=90°,
∴∠ACD+∠CAD=90°,∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∠ADC=∠CEB=90°;∠CAD=∠BCE,AC=BC,
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∵点C的坐标为(1,2),点A的坐标为(?2,0),
∴AD=CE=3,OD=1,BE=CD=2,
∴则B点的坐标是(3,?1).
故答案为(3,?1).
分析:过C和B分别作CD⊥OD于D,BE⊥CD于E,利用已知条件可证明△ADC≌△CEB,再由全等三角形的性质和已知数据即可求出B点的坐标.
13. 6
考点:坐标与图形性质
解:∵AD⊥BC,BO⊥AC,
∴∠OAD+∠ACB=90°;∠OBC+∠ACB=90°
∴∠OAD=∠OBC,∠BOC=∠AOD=90°,
又∵AD=BC,
∴△AOD≌△BOC,
∴AO=BO=3,
又∵CO=1,
∴AC=4,
∴△ABC的面积为 ×AC×BO= ×4×3=6,
故答案为:6.
分析:依据AD⊥BC,BO⊥AC,AD=BC,即可得到△AOD≌△BOC,进而得出AO=BO=3,再根据△ABC的面积= ×AC×BO,即可得到结论.
14. (3,2)
考点:坐标与图形性质
解:根据题意,可设出P点的横坐标为x,纵坐标为x-1,
x+x-1=5,解得x=3,又∵x-1=2
∴P点坐标为(3,2)
分析:根据P点的横纵坐标的关系,可列出方程,解出x的值即可。
三、解答题
15. (1)由平面直角坐标系可知:点A(-1,-1),点B(4,2),点C(1,3);
(2)用一个矩形将△ABC框住,如图所示
S△ABC=5×4- ×4×2- ×5×3- ×3×1=7
考点:坐标与图形性质
分析:(1)根据平面直角坐标系即可写出各个点的坐标;(2)用一个矩形将△ABC框住,然后用矩形的面积减去3个直角三角形的面积即可求出结论.
16. 解:过点B作BE⊥x轴于点E,如下图所示:
四边形ABCD分成△AOD,梯形BEOA,△BCE,
S△AOD= ×OD×OA= ×1×4=2,
S梯形BEOA= ×(BE+OA)×OE= ×(3+4)×3= ,
S△BCE= ×CE×BE= ×2×3=3,
S四边形ABCD=2+ +3=15.5,
即四边形ABCD的面积为15.5.
考点:坐标与图形性质
分析: 过点B作BE⊥x轴于点E,如图,?由S四边形ABCD= S△AOD+ S梯形BEOA+ S△BCE , 利用梯形的面积公式及三角形的面积公式计算即可.
17. (1)点A
(2)由题意可知: ,
①当m>0时,则4m=4,
解得m=1;
②当m<0时,则﹣4m=4,
解得m=﹣1;
∴m=±1.
考点:坐标与图形性质
解:(1)根据题意,对于点A而言,|2|+|2|=4,
所以A是“垂距点”,
对于点B而言,| |+|﹣ |=3,
所以B不是“垂距点”,
对于点C而言,|﹣1|+|5|=6≠4,
所以C不是“垂距点”,
故答案为:点A .
分析:(1)根据题意即可解答;(2)根据“垂距点”的定义,得到 ,解得m的值即可.
18. (1)由 |a+2|+ =0 可知|a+2|=0, =0
则a=-2, b=4?? AB=6
S三角形ABC==9
(2)∵M在x轴上,∴△ACM和△ABC的高相等,
AB的长度为6,面积关系为 S三角形ACM= S三角形ABC
则AM=AB?
所以点M的坐标为(0,0)或(-4,0)
考点:坐标与图形性质
分析:(1)利用绝对值与偶次幂的非负性可求出a、b的值,从而得出三角形的面积。
(2)根据面积关系,可求得点M的坐标。
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册4.2 平面直角坐标系(2)同步练习
一、单选题
1.如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是(??? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
2.如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的 ,则点A的对应点A′的坐标是(??? )
A.?(2,3)?????????????????????????????????B.?(6,1)?????????????????????????????????C.?(2,1)?????????????????????????????????D.?(3,3)
3.如图,在平面直角坐标系中,已知点B,C在x轴上,AB⊥x轴于点B,DA⊥AB.若AD=5,点A的坐标为(-2,7),则点D的坐标为(?? )
A.?(-2,2)?????????????????????????????B.?(-2,12)?????????????????????????????C.?(3,7)?????????????????????????????D.?(-7,7)
4.如图,△ABC顶点C的坐标是(1,-3),过点C作AB边上的高线CD,则垂足D点坐标为( )
A.?(1,0)??????????????????????????B.?(0,1)??????????????????????????C.?(-3,0)??????????????????????????D.?(0,-3)
5.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( ??)
A.?(1,3)??????????????????????B.?(3,﹣1)??????????????????????C.?(﹣1,﹣3)??????????????????????D.?(﹣3,1)
6.如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为(?? )
A.?(3,1)??????????????????????????????B.?(-1,1)??????????????????????????????C.?(3,5)??????????????????????????????D.?(-1,5)
7.已知点A(1,0),B(0,3),点P在x轴上,且三角形PAB的面积为3,则点P的坐标是(??? )
A.?(﹣1,0)???????????B.?(3,0)???????????C.?(﹣1,0)或(3,0)???????????D.?(0,9)或(0,﹣3)
8.已知P(a,b)是第一象限内的矩形ABCD(含边界)中的一个动点,A,B,C,D的坐标如图所示,则 的最大值与最小值依次是(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
二、填空题
9.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为________.
10.如图,在平面直角坐标系中, 的顶点A,B的坐标分别为 , ,把 沿x轴向右平移得到 ,如果点D的坐标为 ,则点E的坐标为________.
11.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是________.
12.如图,∠ACB=90°,AC=BC,点C(1,2)、A(-2,0),则点B的坐标是________.
13.如图,在△ABC的顶点均在坐标轴,AD⊥BC交于点E,且AD=BC,点B.C的坐标分别为B(0,3),C(1,0),则△ABC的面积是________.
14.如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的点角距离”,记为d(P,∠MON)如图乙,在平面直角坐标系xOy中,点P在坐标平面内,且点P的横坐标比织坐标大1,对于∠xOy,满足d(P,∠xOy)=5,点P的坐标是________?.
三、解答题
15.如图,△ABC 在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积;
16.如图,已知四边形ABCD,则四边形ABCD的面积是多少?
17.点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
(1)在点A(﹣2,2), ,C(﹣1,5)是“垂距点”是________;
(2)若 是“垂距点”,求m的值.
18.如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+ =0,点C的坐标为(0,3)。
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM= S三角形ABC , 试求点M的坐标。
答案解析部分
一、单选题
1. D
考点:点的坐标,正方形的性质
解:∵O , D两点的坐标分别是 , ,
∴OD=6,
∵四边形 是正方形,
∴OB⊥BC , OB=BC=6
∴C点的坐标为: ,
故答案为:D .
分析:利用O , D两点的坐标,求出OD的长度,利用正方形的性质求出OB , BC的长度,进而得出C点的坐标即可.
2. A
考点:坐标与图形性质
解:点A变化前的坐标为(6,3),
将纵坐标保持不变,横坐标变为原来的 ,
则点A的对应点A′坐标是(2,3).
故答案为:A.
分析:先写出点A的坐标为(6,3),纵坐标保持不变,横坐标变为原来的 ,即可判断出答案.
3. C
考点:坐标与图形性质
解:如图,设AD与y轴的交点为E,
在直角梯形ABCD中,∵点A的坐标为(-2,7),
∴OB=2,OE=7,
∵AD=5,
∴DE=5-2=3,
∴点D的坐标为(3,7).
故答案为:C.
分析:根据图形中点A的坐标和DA⊥AB、AB⊥x轴,得到AD⊥y轴,再由AD=5,得到点D的坐标.
4. A
考点:坐标与图形性质
解:如图,
∵CD⊥x轴,
∴CD∥y轴,
∵点C的坐标是(1,-3),
∴点D的横坐标为1,
∵点D在x轴上,
∴点D的纵坐标为0,
∴点D的坐标为(1,0).
故答案为:A.
分析:根据在同一平面内,垂直于同一直线的两直线平行可得CD∥y轴,再根据平行于y轴上的点的横坐标相同解答.
5.D
考点:坐标与图形性质
解:如图,由点A、E的坐标分别为(a,b)、(﹣a,b)知A、E两点关于y轴对称,
则B、D两点也关于y轴对称,
∵B(3,1),
∴D(﹣3,1),
故选:D.
分析:由A、E两点的纵坐标相等而横坐标互为相反数知A、E两点关于y轴对称,结合图形知B、D两点也关于y轴对称,据此可得答案.
6.C
考点:坐标与图形性质
解:∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,
∴点B的横坐标为:﹣1+4=3,纵坐标为:1,
∴点B的坐标为(3,1),
∴点C的横坐标为:3,纵坐标为:1+4=5,∴点C的坐标为(3,5).
故答案为:C
分析:根据正方形的性质及边长为4,点A的坐标为(﹣1,1),就可得出点C的坐标。
7. C
考点:坐标与图形性质
解:如图,设P(m , 0),
由题意: ?|1﹣m|?3=3,
∴m=﹣1或3,
∴P(﹣1,0)或(3,0),
故答案为:C .
分析:根据题意画出图像,由三角形的面积公式即可求解判断.
8. B
考点:坐标与图形性质
解:如图所示:当 取最大值时:即a最小,b最大,则a=m,b=p,
∴ 的最大值为: ,
当 取最小值时:即a最大,b最小,则a=n,b=q,
∴ 的最小值为: .
故答案为:B
分析:P(a,b)是第一象限内的矩形ABCD(含边界)中的一个动点,要求的最大值,则需要满足a最小,b最大,则a=m,b=p,从而得出答案;要求的最小值,则需要满足a最大,b最小,则a=n,b=q,,根据除法的意义得出答案。
二、填空题
9. (15,3)
考点:坐标与图形性质
解:设正方形的边长为 ,
则由题设条件可知:
解得:
点A的横坐标为: ,点A的纵坐标为:
故点A的坐标为 .
故答案为: .
分析:先根据条件,算出每个正方形的边长,再根据坐标的变换计算出点A的坐标即可.
10. (7,0)
考点:坐标与图形性质
解:由题意知:A、B两点之间的横坐标差为: ,
由平移性质可知:E、D两点横坐标之差与B、A两点横坐标之差相等,
设E点横坐标为a,
则a-6=1,∴a=7,
∴E点坐标为(7,0) .
故答案为:(7,0) .
分析:根据B点横坐标与A点横坐标之差和E点横坐标与D点横坐标之差相等即可求解.
11. (3,0)
考点:坐标与图形性质
解:∵ 正方形ABCD的顶点B、C都在直角坐标系的x轴上,点A的坐标是(-1,4)
∴BC=AB=4,B(-1,0)
∴点C的坐标是(3,0).
分析:根据点A的坐标即可确定正方形的边长及点B的坐标,从而求得点C的坐标.
12. (3,-1)
考点:坐标与图形性质
解:过C和B分别作CD⊥OD于D,BE⊥CD于E,
∵∠ACB=90°,
∴∠ACD+∠CAD=90°,∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∠ADC=∠CEB=90°;∠CAD=∠BCE,AC=BC,
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∵点C的坐标为(1,2),点A的坐标为(?2,0),
∴AD=CE=3,OD=1,BE=CD=2,
∴则B点的坐标是(3,?1).
故答案为(3,?1).
分析:过C和B分别作CD⊥OD于D,BE⊥CD于E,利用已知条件可证明△ADC≌△CEB,再由全等三角形的性质和已知数据即可求出B点的坐标.
13. 6
考点:坐标与图形性质
解:∵AD⊥BC,BO⊥AC,
∴∠OAD+∠ACB=90°;∠OBC+∠ACB=90°
∴∠OAD=∠OBC,∠BOC=∠AOD=90°,
又∵AD=BC,
∴△AOD≌△BOC,
∴AO=BO=3,
又∵CO=1,
∴AC=4,
∴△ABC的面积为 ×AC×BO= ×4×3=6,
故答案为:6.
分析:依据AD⊥BC,BO⊥AC,AD=BC,即可得到△AOD≌△BOC,进而得出AO=BO=3,再根据△ABC的面积= ×AC×BO,即可得到结论.
14. (3,2)
考点:坐标与图形性质
解:根据题意,可设出P点的横坐标为x,纵坐标为x-1,
x+x-1=5,解得x=3,又∵x-1=2
∴P点坐标为(3,2)
分析:根据P点的横纵坐标的关系,可列出方程,解出x的值即可。
三、解答题
15. (1)由平面直角坐标系可知:点A(-1,-1),点B(4,2),点C(1,3);
(2)用一个矩形将△ABC框住,如图所示
S△ABC=5×4- ×4×2- ×5×3- ×3×1=7
考点:坐标与图形性质
分析:(1)根据平面直角坐标系即可写出各个点的坐标;(2)用一个矩形将△ABC框住,然后用矩形的面积减去3个直角三角形的面积即可求出结论.
16. 解:过点B作BE⊥x轴于点E,如下图所示:
四边形ABCD分成△AOD,梯形BEOA,△BCE,
S△AOD= ×OD×OA= ×1×4=2,
S梯形BEOA= ×(BE+OA)×OE= ×(3+4)×3= ,
S△BCE= ×CE×BE= ×2×3=3,
S四边形ABCD=2+ +3=15.5,
即四边形ABCD的面积为15.5.
考点:坐标与图形性质
分析: 过点B作BE⊥x轴于点E,如图,?由S四边形ABCD= S△AOD+ S梯形BEOA+ S△BCE , 利用梯形的面积公式及三角形的面积公式计算即可.
17. (1)点A
(2)由题意可知: ,
①当m>0时,则4m=4,
解得m=1;
②当m<0时,则﹣4m=4,
解得m=﹣1;
∴m=±1.
考点:坐标与图形性质
解:(1)根据题意,对于点A而言,|2|+|2|=4,
所以A是“垂距点”,
对于点B而言,| |+|﹣ |=3,
所以B不是“垂距点”,
对于点C而言,|﹣1|+|5|=6≠4,
所以C不是“垂距点”,
故答案为:点A .
分析:(1)根据题意即可解答;(2)根据“垂距点”的定义,得到 ,解得m的值即可.
18. (1)由 |a+2|+ =0 可知|a+2|=0, =0
则a=-2, b=4?? AB=6
S三角形ABC==9
(2)∵M在x轴上,∴△ACM和△ABC的高相等,
AB的长度为6,面积关系为 S三角形ACM= S三角形ABC
则AM=AB?
所以点M的坐标为(0,0)或(-4,0)
考点:坐标与图形性质
分析:(1)利用绝对值与偶次幂的非负性可求出a、b的值,从而得出三角形的面积。
(2)根据面积关系,可求得点M的坐标。
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
