3.2 图形的旋转同步练习(含解析）

中小学教育资源及组卷应用平台
初中数学浙教版九年级上册3.2图形的旋转 同步练习
一、单选题
1.在绿色食品、回收、节能、节水四个标志中，是由某个基本图形经过旋转得到的是（?? ）
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
2.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是（?? ）
A.?逆时针旋转90°???????????????B.?顺时针旋转90°???????????????C.?逆时针旋转45°???????????????D.?顺时针旋转45°
3.如图，在Rt△ABC中，∠BAC=90°，将Rt△ABC绕点C按逆时针方向旋转46°得到Rt△A′B′C，点A在边B′C上，则∠ACB的大小为（?? ）
A.?23°???????????????????????????????????????B.?44°???????????????????????????????????????C.?46°???????????????????????????????????????D.?54°
4.如图所示是一个旋转对称图形，若将它绕自身中心旋转一定角度之后不能与原图重合，则这个角度可能是 ??
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
5.如图，在平面直角坐标系中，△ABC的顶点都在方格线的格点上，将△ABC绕点P顺时针方向旋转90°，得到△A′B′C′，则点P的坐标为（　　）
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
6.如图，在正方形网格中，线段A′B′是线段AB绕某点顺时针旋转一定角度所得，点A′与点A是对应点，则这个旋转的角度大小可能是（?? ）
A.?45°??????????????????????????????????????B.?60°??????????????????????????????????????C.?90°??????????????????????????????????????D.?135°
7.如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（?? ）
A.?点M??????????????????????????????????B.?格点N??????????????????????????????????C.?格点P??????????????????????????????????D.?格点Q
8.一辆模型赛车，先前进1m，然后沿原地逆时针方向旋转，旋转角为a(0A.?108°?????????????????????????????????????B.?120°?????????????????????????????????????C.?72 °?????????????????????????????????????D.?36°
9.如图，教室里有一只倒地的装垃圾的灰斗，BC与地面的夹角为50°，∠C=25°，小贤同学将它绕点C旋转一定角度，扶起平放在地面上(如图)，则灰斗柄AB绕点C转动的角度为（? ?）
A.?75°?????????????????????????????????????B.?25°?????????????????????????????????????C.?115°?????????????????????????????????????D.?105°
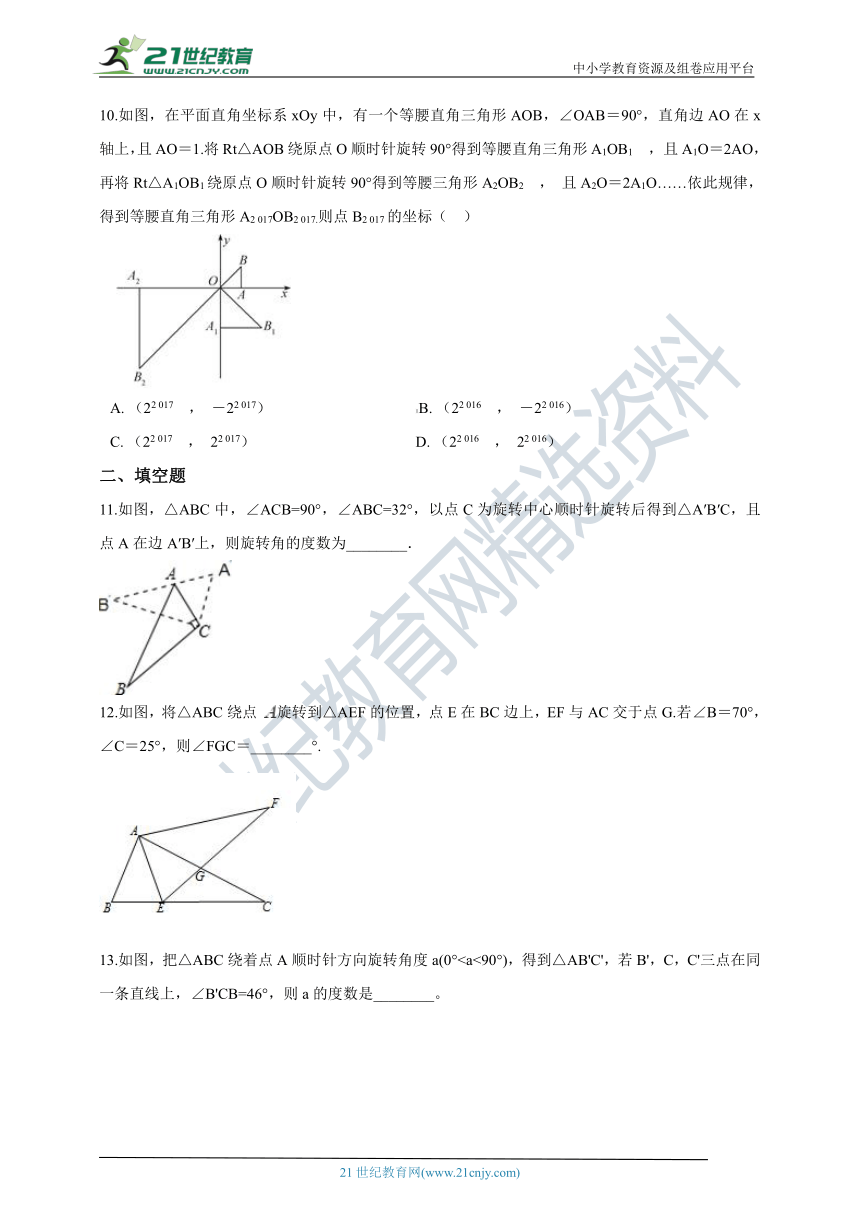
10.如图，在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB＝90°，直角边AO在x轴上，且AO＝1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1 ， 且A1O＝2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2 ， 且A2O＝2A1O……依此规律，得到等腰直角三角形A2 017OB2 017.则点B2 017的坐标（?? ）
A.?（22 017 ， －22 017）??????????????????????????????????????B.?（22 016 ， －22 016）
C.?（22 017 ， 22 017）??????????????????????????????????????????D.?（22 016 ， 22 016）
二、填空题
11.如图，△ABC中，∠ACB=90°，∠ABC=32°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为________．
12.如图，将△ABC绕点 旋转到△AEF的位置，点E在BC边上，EF与AC交于点G.若∠B＝70°，∠C＝25°，则∠FGC＝________°.
13.如图，把△ABC绕着点A顺时针方向旋转角度a(0°
14.如图所示，用一张斜边长为25的红色直角三角形纸片，一张斜边长为50的蓝色直角三角形纸片，一张黄色的正方形纸片，恰好能拼成一个直角三角形，则红、蓝两张三角形纸片的面积之和是________.
15.如图，△ABC为等边三角形，△AO′B绕点A逆时针旋转后能与△AOC重合，则∠OAO′＝________度．
三、解答题
16.如图，△DEF是由△ABC通过一次旋转得到的，请用直尺和圆规画出旋转中心．
17.画出△ABC关于点O中心对称的图形．

18.如图所示，在Rt△ABC中,∠BAC=90°，AC=AB，∠DAE=45°,且BD=3，CE=4 ,求DE的长.
19.如图所示是某设计师设计的方桌布图案的一部分，请你在坐标纸（就是此方格纸）上画出该图形绕原点顺时针依次旋转90°、180°、270°后的图形，并判断所画图形是什么图形．

20.如图，点E是正方形ABCD的边AB上一点，AB=4，DE=4.3，△DAE逆时针旋转后能够与△DCF重合.

（1）旋转中心是________，旋转角为________ ；
（2）请你判断△DFE的形状，简单说明理由；
（3）四边形DEBF的面积为________.
21.如图，△ABC与△ADE都是等腰直角三角形，连接CD、BE ， CD、BE相交于点O ， △BAE可看作是由△CAD顺时针旋转所得．
（1）旋转中心是________，旋转角度是________；
（2）判断CD与BE的位置关系，并说明理由．
答案解析部分
一、单选题
1. B
考点：图形的旋转
解：ACD、 不是由某个基本图形经过旋转得到的，故ACD不符合题意；
B、是由一个基本图形经过旋转得到的，故B符合题意.
故答案为：B.
分析：根据旋转的特征，逐项进行判断，即可求解.
2. A
考点：旋转的性质
解：根据图形可知：将△ABC绕点A逆时针旋转90°可得到△ADE，
故答案为：A.
分析：根据给出的图形先确定出旋转中心，再确定出旋转的方向和度数即可求出答案.
3. C
考点：旋转的性质
解：由旋转得：∠ACA′=∠ACB=46°，
故答案为：C.
分析：根据题意：Rt△ABC绕点C按逆时针方向旋转46°得到Rt△A′B′C，即旋转角为46°，则∠ACB=46°即可得解.
4. B
考点：旋转的性质
解：如图，观察图形可知：
旋转角是 的倍数时，旋转后可以与原来图形重合，
故性质 不可能与原来图形重合，
故选：
分析：如图，观察图形可知： ，推出旋转角是 的倍数时，旋转后可以与原来图形重合，由此即可判断
5. C
考点：旋转的性质
解：由图知，旋转中心P的坐标为（1，2），
故答案为：C．
分析：选两组对应点，连接后作其中垂线，两中垂线的交点即为点P．
6. C
考点：旋转的性质
解：如图：
连接AA′，BB′，作线段AA′，BB′的垂直平分线交点为O，点O即为旋转中心.连接OA，OB′，∠AOA′即为旋转角，
∴旋转角为90°
故答案为：C.
分析：如图：连接AA′，BB′，作线段AA′，BB′的垂直平分线交点为O，点O即为旋转中心.连接OA，OB′，∠AOA′即为旋转角.
7. B
考点：旋转的性质
解：如图，连接N和两个三角形的对应点；
?
发现两个三角形的对应点到点N的距离相等，因此格点N就是所求的旋转中心；
故答案为：B.
分析：此题可根据旋转前后对应点到旋转中心的距离相等来判断所求的旋转中心.
8. C
考点：图形的旋转，旋转的性质
解：根据题意可知，赛车原地绕了一圈，旋转角为360°÷5=72°。
分析：根据赛车旋转五次后回到出发点，即可得到其旋转的角度之和为360°，即可得到答案。
9. D
考点：旋转的性质
解：如图：连结AC并且延长至E，
因为∠DCE=180°-∠DCB-∠ACB=105°，即旋转角为105°，
所以灰斗柄AB绕点C转动的角度为105°．
故答案为：D．
分析：如图,连结AC并且延长至E，根据平角的定义求出∠ECD的度数即可.
10. A
考点：坐标与图形变化﹣旋转
解：∵将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1 ， 且A1O=2AO，A1B 1=OA1 ， 再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2 ， 且A2O=2A1O，A2B2=A2O…，依此规律，
∴每4次循环一周，B1（2，﹣2），B2（﹣4，-4），B3（-8，8），B4（16，16），
∵2017÷4=504…1，
∴点B2017与B1同在第四象限，
∵﹣4=﹣22 ， 8=23 ， 16=24 ，
∴点B2017（22017 ， -22017），
故答案为：A.
分析：根据旋转的条件发现每4次旋转一周，且B1（2，﹣2），B2（﹣4，-4），B3（-8，8），B4（16，16）……，因为2017÷4=504……1，所以可得点B2017与B1同在第四象限，由于B1（21 ， ﹣21），从而可得点B2017（22017 ， -22017）。
二、填空题
11. 64°
考点：旋转的性质
解：∵∠ACB=90°，∠ABC=32°，
∴∠BAC=58°，
∵以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，
∴CA=CA′，∠A′=∠BAC=58°，∠ACA′等于旋转角，
∴∠CAA′=∠A′=58°，
∴∠ACA′=180°-58°-58°=64°，
即旋转角的度数为64°．
故答案为：64°．
分析：先利用互余计算出∠BAC=58°，再利用旋转的性质得CA=CA′，∠A′=∠BAC=58°，∠ACA′等于旋转角，根据等腰三角形的性质和三角形内角和计算出∠ACA′的度数即可．
12. 65
考点：旋转的性质
解：由旋转的性质可得：AB=AE，∠BAC=∠EAF，
又∵∠B＝70°，
∴∠BAE=180°-2×70°=40°，
∵∠BAC=∠EAF，
∴∠BAE=∠FAG=40°，
∵△ABC≌△AEF，
∴∠F=∠C=25°，
∴∠FGC=∠FAG+∠F=40°+25°=65°，
故答案为：65.
分析：根据旋转前后的图形全等，可推出∠BAE=∠FAG=40°，∠F=∠C=25°，根据三角形外角的性质即可求解.
13. 46
考点：旋转的性质
解：∵把△ABC绕着点A顺时针方向旋转角度a(0° ∴AC=AC＇，∠C＇=∠ACB
∴∠ACC＇=∠AC＇C，=∠ACB
∴∠C＇+∠AC＇C+∠CAC＇=180°
∠ACB+∠ACC＇+∠B'CB=180°
∴∠CAC＇=a=∠B'CB=46°.
故答案为：46.
分析：利用旋转的性质，易证AC=AC＇，∠C＇=∠ACB，利用等边对等角，可证得∠ACC＇=∠AC＇C，=∠ACB，再利用平角的定义及三角形内角和定理可推出∠CAC＇=a=∠B'CB。
14. 625
考点：旋转的性质
解：如图所示：
将△BDC逆时针旋转到△FBE位置，
则红、蓝两张三角形纸片的面积之和为Rt△ABE的面积为： ×25×50＝625
故填：625.
分析：利用旋转的性质得出红、蓝两张三角形纸片的面积之和为Rt△ABE的面积，即可得出答案．
15. 60
考点：旋转的性质
解：根据旋转的性质得：∠OAO′=∠BAC ．
∵△ABC是等边三角形，∴∠BAC=60°，∴∠OAO′=60°．
故答案为60．
分析：根据旋转的性质，找出∠OAO′=∠BAC ， 根据等边三角形的性质，即可解答．
三、解答题
16.解：如图所示，点P即为所求作的旋转中心．
考点：作图﹣旋转
分析：利用旋转的性质，连接BE，AD，分别作出线段BE、AD的垂直平分线，两垂直平分线的交点就是旋转中心。
17.解：所作图形如下：
考点：作图-旋转变换
分析：根据中心对称点平分对应点连线，可得出各点的对应点，顺次连接即可得出△ABC关于点O中心对称的图形．
18. 如图,因为 为等腰直角三角形,所以 .
所以把 绕点 旋转到 ,则 .
所以 .连结 .
所以 为直角三角形.
由勾股定理,得 .所以 .
因为 所以 .
所以 .
所以 .
考点：全等三角形的判定与性质，等腰三角形的性质，勾股定理，旋转的性质
分析：把 绕点 顺时针旋转到 ，连接 ，根据等腰三角形的性质结合旋转的性质可得出 ， ，利用勾股定理可求出 的长度，由 ，结合 ， 即可证出 ，再根据等腰三角形的性质即可求出 的长度.
19.解：如图所示：

考点：利用旋转设计图案
分析：在方格纸上将该图形的各顶点绕点O顺时针依次旋转90°、180°、270°后得到对应点，顺次连接，画出它变换后的图形．即可判断所画图形是什么图形．
20. （1）点D；90
（2）解：△DFE是等腰直角三角形.
理由：根据旋转可得DE=DF，∠EDF=∠ADC=90° ，
所以△DFE是等腰直角三角形.
（3）16
考点：旋转的性质
解：（1）根据旋转的性质可得，旋转中心是点D，旋转角是∠ADC=90°.
故答案为：点D，90
（ 3 ）解：根据旋转可得：△ADE≌△CDF，
∴四边形DEBF的面积=正方形ABCD的面积=4×4=16.
故答案为：16.
分析：（1）依据△DAE逆时针旋转后能够与△DCF重合，即可得到旋转中心以及旋转角的度数；（2）根据旋转可得DE＝DF，∠EDF＝∠ADC＝90°，即可得到△DFE是等腰直角三角形；
（3）根据△ADE≌△CDF，即可得到：四边形DEBF的面积＝正方形ABCD的面积，从而即可得出答案.
21. （1）点A；90°
（2）解：CD⊥BE
理由如下：∵△BAE可看作是由△CAD顺时针旋转所得，
∴△ACD≌△ABE
∴∠ACD＝∠ABE ，
∵在Rt△ABC中，∠ACD+∠BCD+∠ABC＝90°，
∴∠BCD+∠ABC+∠ABE＝90°
∴∠BOC＝90°
∴CD⊥BE
考点：图形的旋转，旋转的性质
解：（1）由图形可得旋转中心为点A ， 旋转角为∠CAB ， 即旋转角度为90°，
故答案为：点A ， 90°
分析：（1）由图形可得旋转中心为点A ， 旋转角为∠CAB为90°；
（2）由旋转得△ACD≌△ABE ， 再利用全等三角形的性质与角的等量替换即可求得∠BOC＝90°，即得证.
_21?????????è?????(www.21cnjy.com)_