3.6 圆内接四边形同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学浙教版九年级上册3.6圆内接四边形 同步练习
一、单选题
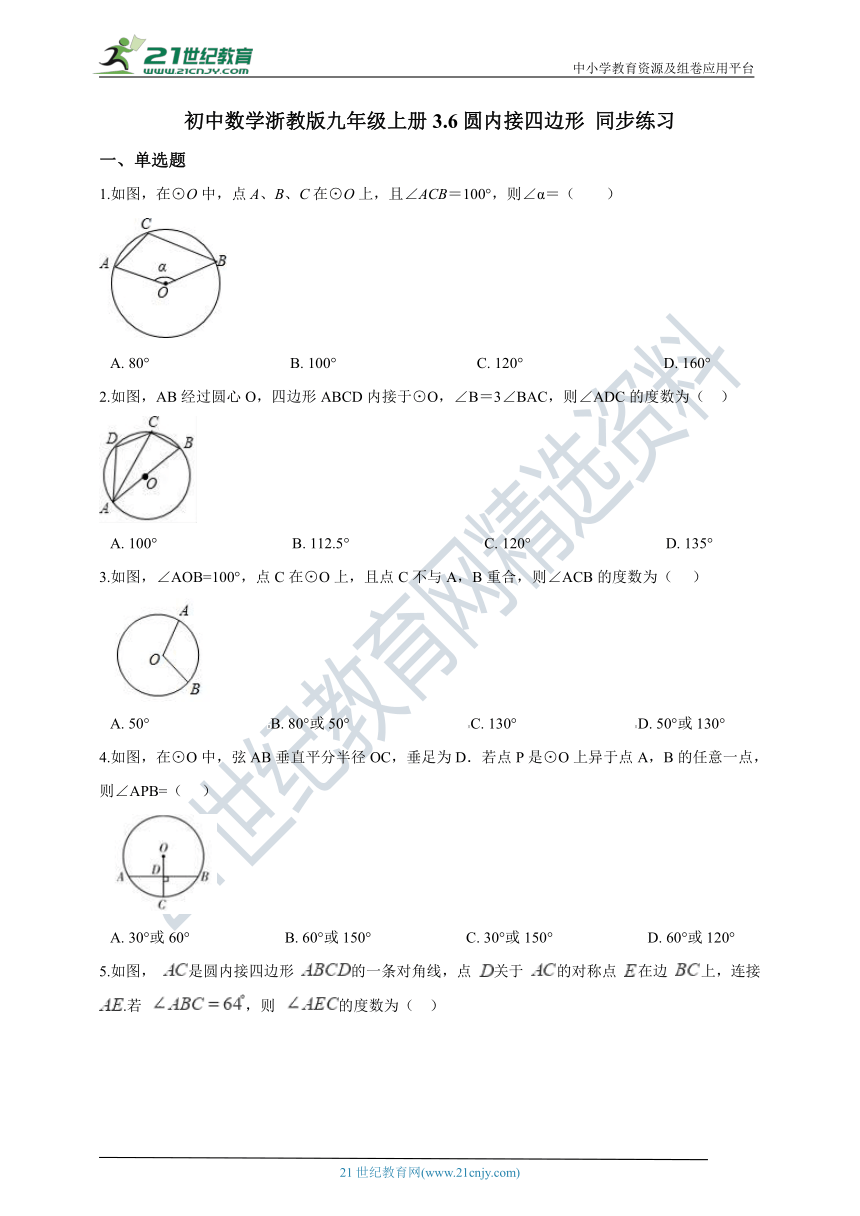
1.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=100°,则∠α=( )
A.?80°?????????????????????????????????????B.?100°?????????????????????????????????????C.?120°?????????????????????????????????????D.?160°
2.如图,AB经过圆心O,四边形ABCD内接于⊙O,∠B=3∠BAC,则∠ADC的度数为(?? )
A.?100°???????????????????????????????????B.?112.5°???????????????????????????????????C.?120°???????????????????????????????????D.?135°
3.如图,∠AOB=100°,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( ???)
A.?50°???????????????????????????????B.?80°或50°???????????????????????????????C.?130°???????????????????????????????D.?50°或130°
4.如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=(??? )
A.?30°或60°?????????????????????????B.?60°或150°?????????????????????????C.?30°或150°?????????????????????????D.?60°或120°
5.如图, 是圆内接四边形 的一条对角线,点 关于 的对称点 在边 上,连接 .若 ,则 的度数为(?? )
A.?106°????????????????????????????????????B.?116°????????????????????????????????????C.?126°????????????????????????????????????D.?136°
6.在圆内接四边形ABCD中, 与 的比为3:2,则∠B的度数为(??? )
A.?36°?????????????????????????????????????B.?72°?????????????????????????????????????C.?108°?????????????????????????????????????D.?216°
7.如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆。点D在弧 上(不与A,C重合),点E在AB上,且点D.E关于AC对称. 给出下列结论:
①若∠ACE=20°,则∠BAC=25°②若BC=3,AC=4,则 给出下列判断,正确的是(??? )
A.?①②都对???????????????????????B.?①②都错???????????????????????C.?①对②错????????????????????????D.?①错②对
8.如图所示A、B、C、D四点在⊙O上的位置,其中 =180°,且 = , = .若阿超在 上取一点P,在 上取一点Q,使得∠APQ=130°,则下列叙述何者正确(??? )
A.?Q点在 上,且 > ?????????????????????????????B.?Q点在 上,且 <
C.?Q点在 上,且 > ????????????????????????????D.?Q点在 上,且 <
9.已知:正方形ABCD内接于⊙O , 点P是⊙O上不同于点B、C的任意一点,则∠BPC的度数是(?? ).
A.?45°??????????????????????????????????B.?90°??????????????????????????????????C.?135°??????????????????????????????????D.?45°或135°
10.如图,四边 内接于 ,若 ,则 的度数为( )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
二、填空题
11.在⊙O中,若一条弦AB的长等于这个圆的半径,则这条弦AB所对的圆周角是________(注意:有两种情况,可不要少填哟!)
12.如图,四边形 内接于圆 , 为边 延长线上一点,已知弧 的度数为 ,则 ________.
13.一条弦把圆分成1:2两部分,那么这条弦所对的圆周角的度数为________.
14.如图,四边形ABCD内接于⊙O,OC∥AD,∠DAB=60°,∠ADC=106°,则∠OCB=________°.
15.如图,四边形ABCD内接于⊙O , AE⊥CB交CB的延长线于点E , 若BA平分∠DBE , AD=5,CE= ,则AE=________.
三、解答题
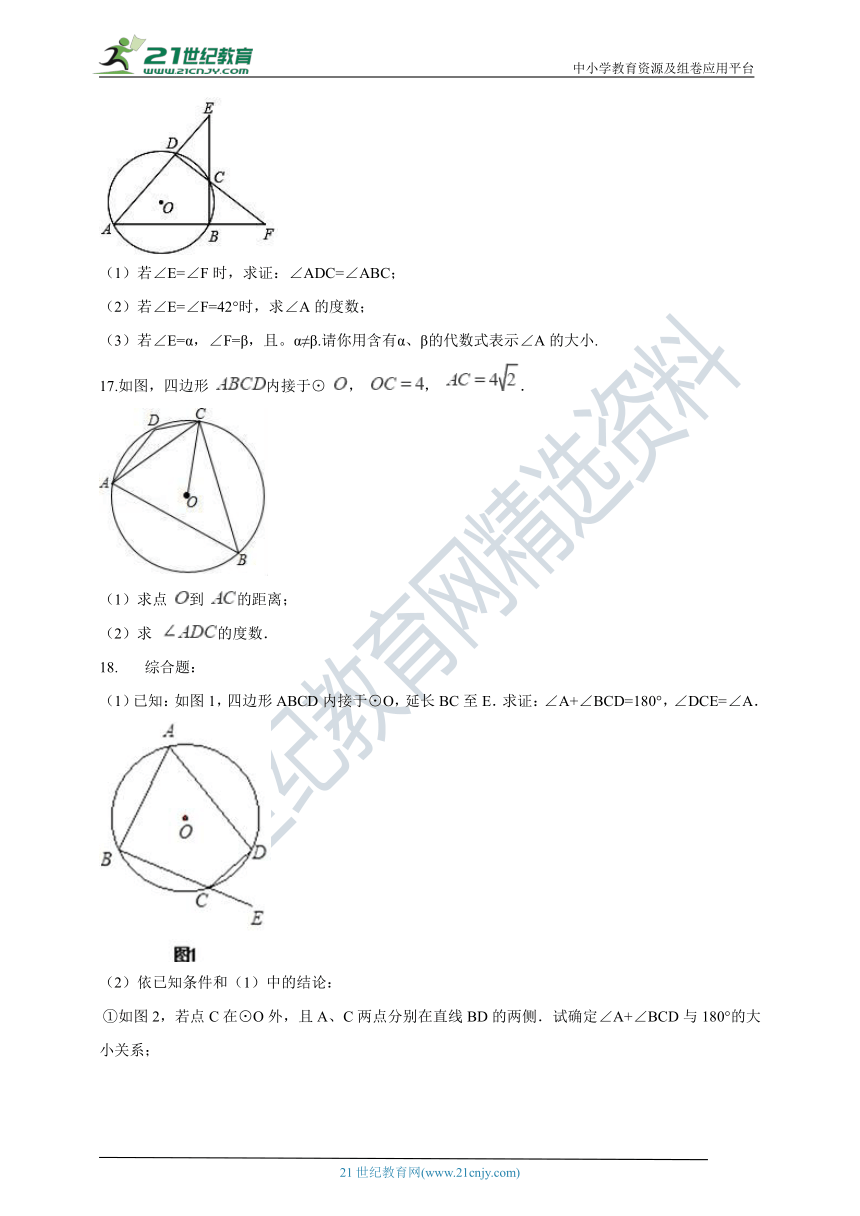
16.如图,⊙ 的内接四边形ABCD两组对边的延长线分别相交于点E、F。
(1)若∠E=∠F时,求证:∠ADC=∠ABC;
(2)若∠E=∠F=42°时,求∠A的度数;
(3)若∠E=α,∠F=β,且。α≠β.请你用含有α、β的代数式表示∠A的大小.
17.如图,四边形 内接于⊙ , , .
(1)求点 到 的距离;
(2)求 的度数.
18.????? 综合题:
(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
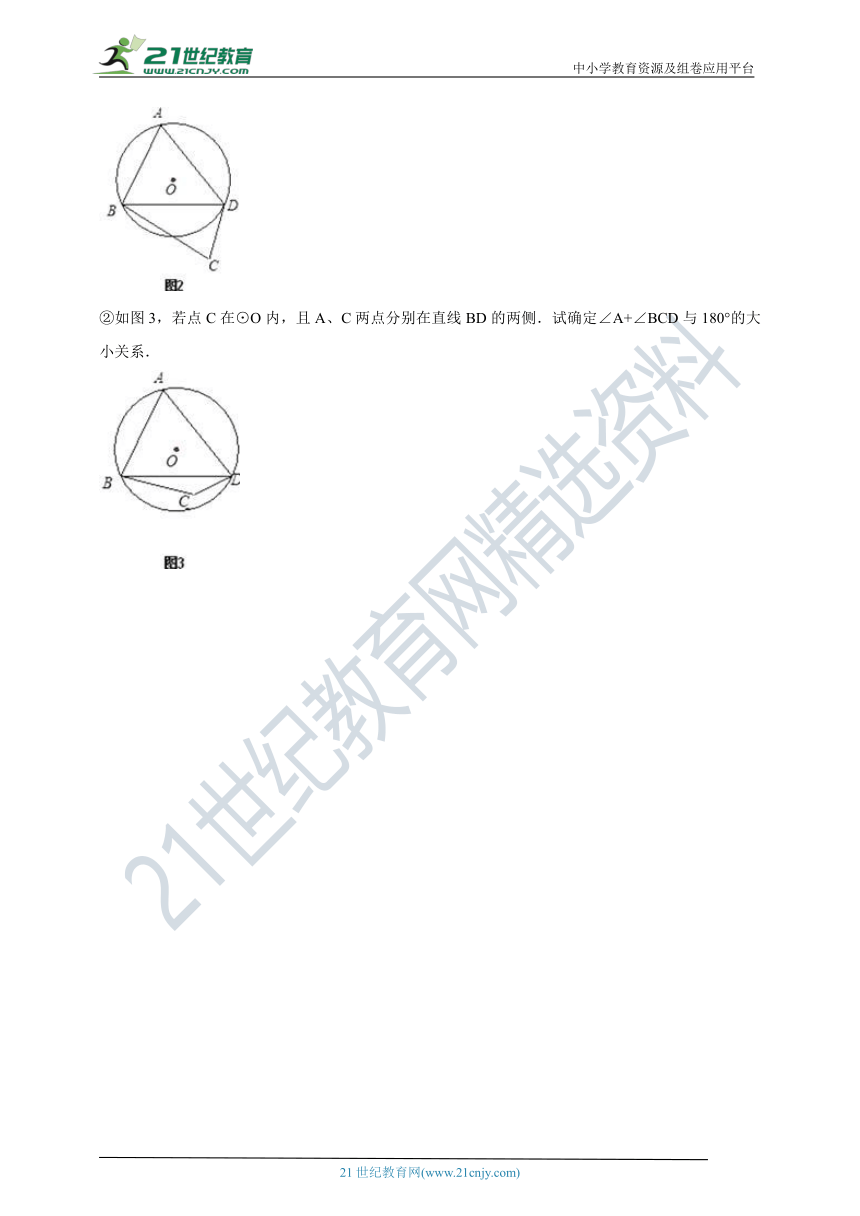
?①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
答案解析部分
一、单选题
1. D
考点:圆周角定理,圆内接四边形的性质
解:优弧AB上任取一点D , 连接AD , BD , .
∵四边形ACBD内接与⊙O , ∠C=100°,
∴∠ADB=180°﹣∠C=180°﹣100°=80°,
∴∠AOB=2∠ADB=2×80°=160°.
故答案为:D .
分析:在优弧AB上任取一点D , 连接AD , BD , 先由圆内接四边形的性质求出∠ADB的度数,再由圆周角定理求出∠AOB的度数即可.
2. B
考点:圆周角定理,圆内接四边形的性质
解:∵AB经过圆心O,
∴∠ACB=90°,
∵∠B=3∠BAC,
∴∠B=67.5°,
∵四边形ABCD内接于⊙O,
∴∠ADC=180°-∠B=112.5°,
故答案为:B.
分析:根据圆周角定理得到∠ACB=90°,根据题意求出∠B,根据圆内接四边形的性质计算即可.
3. D
考点:圆周角定理,圆内接四边形的性质
解:如图,
当点C在优弧AB上时,
∠ACB=∠AOB=×100°=50°;
当点C在劣弧AB上时,
∠C+∠AC1B=180°,
∴∠AC1B=180°-50°=130°.
∴∠ACB的度数为50°或130°.
故答案为:D.
分析:分情况讨论:当点C在优弧AB上时,利用圆周角定理求出∠C的度数;当点C在劣弧AB上时,利用圆内接四边形的性质求出∠AC1B的度数。
4. D
考点:垂径定理,圆周角定理,圆内接四边形的性质
解:连接OA,OB,
∵ 弦AB垂直平分半径OC
∴OD=OA,
∴∠OAD=30°,
∵OA=OB
∴∠OAB=∠OBA=30°,
∴∠AOB=180°-∠OAB-∠OBA=180°-30°-30°=120°;
当点P在优弧AB上时
∠APB=∠AOB=×120°=60°;
当点P在劣弧上时,
∠APB+∠AP1B=180°
∴∠AP1B=180°-60°=120°.
∴∠APB=120°或60°.
故答案为:D.
分析:利用垂径定理及已知可得到∠OAD=30°,再求出∠AOB的度数,再分情况讨论:当点P在优弧AB上时,利用圆周角定理就可取出∠P的度数;当点P在劣弧上时,利用圆内接四边形的对角互补,就可求出∠AP1B的度数。
5. B
考点:圆内接四边形的性质,轴对称的性质
解:∵四边形ABCD是圆的内接四边形,
∴∠D=180°-∠ABC=180°-64°=116°,
∵点D关于 的对称点 在边 上,
∴∠D=∠AEC=116°,
故答案为B.
分析:根据圆的内接四边形对角互补,得出∠D的度数,再由轴对称的性质得出∠AEC的度数即可.
6. C
考点:圆周角定理,圆内接四边形的性质
解:如图,
∵四边形ABCD是圆内接四边形,
∴∠B+∠D=180°,
?∵?与??的比为3:2,
∴∠B:∠D=3:2,
∴∠B=180°×=108°.
故答案为:C.
分析:由?与??的比为3:2,根据圆周角定理可得∠B:∠D=3:2, 结合圆内接四边形对角互补的性质,可求∠B的大小.
7. D
考点:三角形中位线定理,圆周角定理,圆内接四边形的性质
解:连接OC、BD,如图:
两线相交于点F.∵ 点D.E关于AC对称 ,
∴AC是的DE的垂直平分线,
∴AE=AD,CE=CD,
又∵AC=AC
∴△ADC≌△AEC,
∴∠ACE=∠ACD=20°,∠BAC=∠DAC,
∵AB是圆的直径,
∴∠ACB=90°,
∴∠BCD=∠BCA+∠ACD=110°,
∵四边形ABCD是圆的内接四边形,
∴∠BAC=180°-∠BCD=70°,
∴ ∠BAC =∠DAC=35°,故①错误;
在Rt△ABC中,∠ACB=90°, BC=3,AC=4 ,
∴AB=5,∴OB=OC=2.5,
∵∠DBC =∠DAC=35°,
∴BC=CD=3,弧BC=弧CD,
∴OC⊥BD,∴∠BFO=90°,设OF=x,
根据勾股定理得出OB2-OF2=BC2-CF2 ,
即2.52-x2=32-(2.5-x)2 , 解得x=,
∵AB是圆的直径,∴∠BDA=90°,由∵OC⊥BD,∴∠OFB=90°=∠ADB,∴OC∥AD,∵点O是AB的中点,∴AD=2OF=,故②正确.
故答案为:D.
分析:根据轴对称的性质及三角形全等的判断方法判断出△ADC≌△AEC,根据全等三角形的对应角相等得出∠ACE=∠ACD=20°,∠BAC=∠DAC,根据直径所对圆周角是直角及圆内接四边形的对角互补得出∠BAC=70°,从而得出∠BAC =∠DAC=35°,根据圆周角定理得出弧BC=弧CD,从而根据垂径定理得出OC⊥BD,然后根据勾股定理,由OB2-OF2=BC2-CF2 , 建立方程,求解算出OF的长,进而再根据三角形的中位线定理得出AD的长.
8. B
考点:圆周角定理,圆内接四边形的性质
解:连接AD、OB、OC、在弧AD上取点E,连接AE,CE,
∵弧AD的度数为180°,
∴AD是直径,
∵ = , =
∴∠AOB=90°,∠BOC=45°,
∴∠AOC=∠AOB+∠BOC=90°+45°=135°,
∴.
∵∠ABC+∠E=180°,
∴∠ABC=180°-67.5°=122.5°<130°,
∴∠APQ>∠ABC,
∴点Q在上,且
故答案为:B.
分析:连接AD、OB、OC、在弧AD上取点E,连接AE,CE,由已知条件可知AD是直径,根据 = , = , 可分别求出∠BOC和∠AOC的度数,再利用圆内接四边形的对角互补求出∠ABC的度数,可以推出∠APQ>∠ABC,就可得到点Q的位置。
9. D
考点:正方形的性质,圆周角定理,圆内接四边形的性质
解:连接BD,
则BD是直径,
∴△BCD是等腰直角三角形,
∴∠BDC=45°,
∴∠BPC=∠BDC=45°.
如图所示:
∠BP′C+∠P=180°,
∴∠BP′C=135°.
故答案为:45°或135°.
故选D.
分析:连接BD,则BD是直径,△BCD是等腰直角三角形,即∠BDC=45°,根据圆周角定理即可证∠BPC=∠BDC=45°,进而利用P点位置不同得出答案.
10. D
考点:圆周角定理,圆内接四边形的性质
解:∵四边形 内接于
∴
∵
∴ .
故答案为:D.
分析:由圆周角定理知,∠C= ∠BOD=50°.由圆内接四边形的对角互补知,∠A=180°-∠C=130°.
二、填空题
11. 30°或150°.
考点:圆周角定理,圆内接四边形的性质
解:如图,连接OA、OB,∵△OAB中,OA=OB=AB,
∴△OAB是等边三角形,即∠OAB=∠ABO=∠O=60°,
∴∠C=30°,∵四边形ADBC是⊙O的内接四边形,
∴∠D=180°﹣∠C=150°,∴弦AB所对的圆周角的度数为30°或150°.
故答案是:30°或150°.
分析:连接OA、OB,可得△OAB是等边三角形,根据圆周角定理和圆的内接四边形的性质定理,即可求解.
12.
考点:圆内接四边形的性质
解: 弧 的度数为 ,
,
四边形 内接于圆 ,
,
.
故答案为:
分析:由弧 的度数为 可求出 的度数,再根据圆的内接四边形的性质,即可求得 的度数,继而求得答案
13. 60°或120°
考点:圆周角定理,圆内接四边形的性质
解:如图,连接OA、OB.
弦AB将⊙O分为1:2两部分,
则∠AOB= ×360°=120°;
∴∠ACB= ∠AOB=60°,
∠ADB=180°﹣∠60=120°;
故这条弦所对的圆周角的度数为60°或120°.
故答案为:60°或120°
分析:此题有两种情况,连接OA、OB,由已知条件弦AB将⊙O分为1:2两部分,可求出∠AOB的度数,再利用圆周角定理求出∠ACB的度数,然后利用圆内接四边形的对角互补,就可求出∠ADB的度数。
14. 46°
考点:圆内接四边形的性质
解:∵OC∥AD, ∴∠OCD=180°-∠ADC=74°, ∵四边形ABCD内接于⊙O, ∴∠BCD=180°-∠DAB=120°, ∴∠OCD=∠BCD-∠OCD=46°,故答案为:46.
分析:根据平行线的性质求出∠OCD,根据圆内接四边形的性质求出∠BCD,计算即可.
15.
考点:圆周角定理,圆内接四边形的性质
解:连接AC,如图,
∵BA平分∠DBE,
∴∠ABE=∠ABD,
∵∠ABE=∠CDA,∠ABD=∠ACD,
∴∠ACD=∠CDA,
∴AC=AD=5,
∵AE⊥CB,
∴∠AEC=90°,
故答案为:2 .
分析:连接AC,由圆内接四边形的性质和圆周角定理得到∠BAE=∠CDA,∠ABD=∠ACD,从而得到∠ACD=∠CDA,得出AC=AD=5,然后利用勾股定理计算AE的长.
三、解答题
16. (1)解:∠E=∠F,∵∠DCE=∠BCF,∴∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,∴∠ADC=∠ABC.
(2)解:由(1)知∠ADC=∠ABC,∵∠EDC=∠ABC,∴∠EDC=∠ADC,∴∠ADC=90°,∴∠A=90°﹣42°=48°
(3)解:连结EF,如图,∵四边形ABCD为圆的内接四边形,∴∠ECD=∠A,∵∠ECD=∠1+∠2,∴∠A=∠1+∠2,∵∠A+∠1+∠2+∠E+∠F=180°,∴2∠A+α+β=180°,∴∠A=90°﹣ .
考点:圆内接四边形的性质
分析:(1)由三角形外角知识可得∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,再由∠E=∠F,∠EDC=∠ABC,等量代换可得∠ADC=∠ABC。
(2)由(1)知∠ADC=∠ABC,再由∠EDC=∠ABC,等量代换得出∠EDC=∠ADC,最后得出∠A。
(3)连结EF,由四边形ABCD为圆的内接四边形,可得∠ECD=∠A,再由三角形外角可得∠ECD=∠1+∠2,等量代换得出∠A=∠1+∠2,最后由三角形内角和定理可得∠A+∠1+∠2+∠E+∠F=180°,等量代换得出∠A的度数? .
17. (1)解:作 于 ,
∵ ,
∴ ,
∵ ,
∴ ;
(2)解:连接 ,
∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ .
考点:勾股定理,圆内接四边形的性质,等腰直角三角形
分析:(1)作OM⊥AC于M,根据等腰直角三角形的性质得到AM=CM=2 ,根据勾股定理即可得到结论;(2)连接OA,根据等腰直角三角形的性质得到∠MOC=∠MCO=45°,求得∠AOC=90°,根据圆内接四边形的性质即可得到结论.
18. (1)证明:连结AC,BD,
∴∠CAD=∠CBD,∠ABD=∠ACD,∠ADB=∠ACB,∠BAC=∠BDC,
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠CAD+∠BAC+∠ABD+∠CBD+∠ACB+∠ACD+∠ADB+∠BDC=360°,
∴∠CAD+∠BAC+∠ACB+∠ACD=180°,
即∠BAD+∠BCD=180°,
又∵∠DCE+∠BCD=180°,
∴∠BAD=∠DCE.
(2)解:①设BC与⊙O交于点E,连结DE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BED=∠CDE+∠BCD,
∴∠BED>∠BCD,
∴∠A+∠BCD<180°.
②延长DC交⊙O于点E,连结BE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BCD=∠CBE+∠BED,
∴∠BCD>∠BED,
∴∠A+∠BCD>180°.
考点:圆内接四边形的性质
分析:(1)连结AC,BD,由同弧所对的圆周角相等和四边形的内角和为360°,即可得证∠A+∠BCD=180°,再由同角的补角相等可得∠DCE=∠A.
(2)①设BC与⊙O交于点E,连结DE,根据圆的内接四边形对角互补和三角形外角性质,即可得证.
②延长DC交⊙O于点E,连结BE,根据圆的内接四边形对角互补和三角形外角性质,即可得证.
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版九年级上册3.6圆内接四边形 同步练习
一、单选题
1.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=100°,则∠α=( )
A.?80°?????????????????????????????????????B.?100°?????????????????????????????????????C.?120°?????????????????????????????????????D.?160°
2.如图,AB经过圆心O,四边形ABCD内接于⊙O,∠B=3∠BAC,则∠ADC的度数为(?? )
A.?100°???????????????????????????????????B.?112.5°???????????????????????????????????C.?120°???????????????????????????????????D.?135°
3.如图,∠AOB=100°,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( ???)
A.?50°???????????????????????????????B.?80°或50°???????????????????????????????C.?130°???????????????????????????????D.?50°或130°
4.如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=(??? )
A.?30°或60°?????????????????????????B.?60°或150°?????????????????????????C.?30°或150°?????????????????????????D.?60°或120°
5.如图, 是圆内接四边形 的一条对角线,点 关于 的对称点 在边 上,连接 .若 ,则 的度数为(?? )
A.?106°????????????????????????????????????B.?116°????????????????????????????????????C.?126°????????????????????????????????????D.?136°
6.在圆内接四边形ABCD中, 与 的比为3:2,则∠B的度数为(??? )
A.?36°?????????????????????????????????????B.?72°?????????????????????????????????????C.?108°?????????????????????????????????????D.?216°
7.如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆。点D在弧 上(不与A,C重合),点E在AB上,且点D.E关于AC对称. 给出下列结论:
①若∠ACE=20°,则∠BAC=25°②若BC=3,AC=4,则 给出下列判断,正确的是(??? )
A.?①②都对???????????????????????B.?①②都错???????????????????????C.?①对②错????????????????????????D.?①错②对
8.如图所示A、B、C、D四点在⊙O上的位置,其中 =180°,且 = , = .若阿超在 上取一点P,在 上取一点Q,使得∠APQ=130°,则下列叙述何者正确(??? )
A.?Q点在 上,且 > ?????????????????????????????B.?Q点在 上,且 <
C.?Q点在 上,且 > ????????????????????????????D.?Q点在 上,且 <
9.已知:正方形ABCD内接于⊙O , 点P是⊙O上不同于点B、C的任意一点,则∠BPC的度数是(?? ).
A.?45°??????????????????????????????????B.?90°??????????????????????????????????C.?135°??????????????????????????????????D.?45°或135°
10.如图,四边 内接于 ,若 ,则 的度数为( )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
二、填空题
11.在⊙O中,若一条弦AB的长等于这个圆的半径,则这条弦AB所对的圆周角是________(注意:有两种情况,可不要少填哟!)
12.如图,四边形 内接于圆 , 为边 延长线上一点,已知弧 的度数为 ,则 ________.
13.一条弦把圆分成1:2两部分,那么这条弦所对的圆周角的度数为________.
14.如图,四边形ABCD内接于⊙O,OC∥AD,∠DAB=60°,∠ADC=106°,则∠OCB=________°.
15.如图,四边形ABCD内接于⊙O , AE⊥CB交CB的延长线于点E , 若BA平分∠DBE , AD=5,CE= ,则AE=________.
三、解答题
16.如图,⊙ 的内接四边形ABCD两组对边的延长线分别相交于点E、F。
(1)若∠E=∠F时,求证:∠ADC=∠ABC;
(2)若∠E=∠F=42°时,求∠A的度数;
(3)若∠E=α,∠F=β,且。α≠β.请你用含有α、β的代数式表示∠A的大小.
17.如图,四边形 内接于⊙ , , .
(1)求点 到 的距离;
(2)求 的度数.
18.????? 综合题:
(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
?①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
答案解析部分
一、单选题
1. D
考点:圆周角定理,圆内接四边形的性质
解:优弧AB上任取一点D , 连接AD , BD , .
∵四边形ACBD内接与⊙O , ∠C=100°,
∴∠ADB=180°﹣∠C=180°﹣100°=80°,
∴∠AOB=2∠ADB=2×80°=160°.
故答案为:D .
分析:在优弧AB上任取一点D , 连接AD , BD , 先由圆内接四边形的性质求出∠ADB的度数,再由圆周角定理求出∠AOB的度数即可.
2. B
考点:圆周角定理,圆内接四边形的性质
解:∵AB经过圆心O,
∴∠ACB=90°,
∵∠B=3∠BAC,
∴∠B=67.5°,
∵四边形ABCD内接于⊙O,
∴∠ADC=180°-∠B=112.5°,
故答案为:B.
分析:根据圆周角定理得到∠ACB=90°,根据题意求出∠B,根据圆内接四边形的性质计算即可.
3. D
考点:圆周角定理,圆内接四边形的性质
解:如图,
当点C在优弧AB上时,
∠ACB=∠AOB=×100°=50°;
当点C在劣弧AB上时,
∠C+∠AC1B=180°,
∴∠AC1B=180°-50°=130°.
∴∠ACB的度数为50°或130°.
故答案为:D.
分析:分情况讨论:当点C在优弧AB上时,利用圆周角定理求出∠C的度数;当点C在劣弧AB上时,利用圆内接四边形的性质求出∠AC1B的度数。
4. D
考点:垂径定理,圆周角定理,圆内接四边形的性质
解:连接OA,OB,
∵ 弦AB垂直平分半径OC
∴OD=OA,
∴∠OAD=30°,
∵OA=OB
∴∠OAB=∠OBA=30°,
∴∠AOB=180°-∠OAB-∠OBA=180°-30°-30°=120°;
当点P在优弧AB上时
∠APB=∠AOB=×120°=60°;
当点P在劣弧上时,
∠APB+∠AP1B=180°
∴∠AP1B=180°-60°=120°.
∴∠APB=120°或60°.
故答案为:D.
分析:利用垂径定理及已知可得到∠OAD=30°,再求出∠AOB的度数,再分情况讨论:当点P在优弧AB上时,利用圆周角定理就可取出∠P的度数;当点P在劣弧上时,利用圆内接四边形的对角互补,就可求出∠AP1B的度数。
5. B
考点:圆内接四边形的性质,轴对称的性质
解:∵四边形ABCD是圆的内接四边形,
∴∠D=180°-∠ABC=180°-64°=116°,
∵点D关于 的对称点 在边 上,
∴∠D=∠AEC=116°,
故答案为B.
分析:根据圆的内接四边形对角互补,得出∠D的度数,再由轴对称的性质得出∠AEC的度数即可.
6. C
考点:圆周角定理,圆内接四边形的性质
解:如图,
∵四边形ABCD是圆内接四边形,
∴∠B+∠D=180°,
?∵?与??的比为3:2,
∴∠B:∠D=3:2,
∴∠B=180°×=108°.
故答案为:C.
分析:由?与??的比为3:2,根据圆周角定理可得∠B:∠D=3:2, 结合圆内接四边形对角互补的性质,可求∠B的大小.
7. D
考点:三角形中位线定理,圆周角定理,圆内接四边形的性质
解:连接OC、BD,如图:
两线相交于点F.∵ 点D.E关于AC对称 ,
∴AC是的DE的垂直平分线,
∴AE=AD,CE=CD,
又∵AC=AC
∴△ADC≌△AEC,
∴∠ACE=∠ACD=20°,∠BAC=∠DAC,
∵AB是圆的直径,
∴∠ACB=90°,
∴∠BCD=∠BCA+∠ACD=110°,
∵四边形ABCD是圆的内接四边形,
∴∠BAC=180°-∠BCD=70°,
∴ ∠BAC =∠DAC=35°,故①错误;
在Rt△ABC中,∠ACB=90°, BC=3,AC=4 ,
∴AB=5,∴OB=OC=2.5,
∵∠DBC =∠DAC=35°,
∴BC=CD=3,弧BC=弧CD,
∴OC⊥BD,∴∠BFO=90°,设OF=x,
根据勾股定理得出OB2-OF2=BC2-CF2 ,
即2.52-x2=32-(2.5-x)2 , 解得x=,
∵AB是圆的直径,∴∠BDA=90°,由∵OC⊥BD,∴∠OFB=90°=∠ADB,∴OC∥AD,∵点O是AB的中点,∴AD=2OF=,故②正确.
故答案为:D.
分析:根据轴对称的性质及三角形全等的判断方法判断出△ADC≌△AEC,根据全等三角形的对应角相等得出∠ACE=∠ACD=20°,∠BAC=∠DAC,根据直径所对圆周角是直角及圆内接四边形的对角互补得出∠BAC=70°,从而得出∠BAC =∠DAC=35°,根据圆周角定理得出弧BC=弧CD,从而根据垂径定理得出OC⊥BD,然后根据勾股定理,由OB2-OF2=BC2-CF2 , 建立方程,求解算出OF的长,进而再根据三角形的中位线定理得出AD的长.
8. B
考点:圆周角定理,圆内接四边形的性质
解:连接AD、OB、OC、在弧AD上取点E,连接AE,CE,
∵弧AD的度数为180°,
∴AD是直径,
∵ = , =
∴∠AOB=90°,∠BOC=45°,
∴∠AOC=∠AOB+∠BOC=90°+45°=135°,
∴.
∵∠ABC+∠E=180°,
∴∠ABC=180°-67.5°=122.5°<130°,
∴∠APQ>∠ABC,
∴点Q在上,且
故答案为:B.
分析:连接AD、OB、OC、在弧AD上取点E,连接AE,CE,由已知条件可知AD是直径,根据 = , = , 可分别求出∠BOC和∠AOC的度数,再利用圆内接四边形的对角互补求出∠ABC的度数,可以推出∠APQ>∠ABC,就可得到点Q的位置。
9. D
考点:正方形的性质,圆周角定理,圆内接四边形的性质
解:连接BD,
则BD是直径,
∴△BCD是等腰直角三角形,
∴∠BDC=45°,
∴∠BPC=∠BDC=45°.
如图所示:
∠BP′C+∠P=180°,
∴∠BP′C=135°.
故答案为:45°或135°.
故选D.
分析:连接BD,则BD是直径,△BCD是等腰直角三角形,即∠BDC=45°,根据圆周角定理即可证∠BPC=∠BDC=45°,进而利用P点位置不同得出答案.
10. D
考点:圆周角定理,圆内接四边形的性质
解:∵四边形 内接于
∴
∵
∴ .
故答案为:D.
分析:由圆周角定理知,∠C= ∠BOD=50°.由圆内接四边形的对角互补知,∠A=180°-∠C=130°.
二、填空题
11. 30°或150°.
考点:圆周角定理,圆内接四边形的性质
解:如图,连接OA、OB,∵△OAB中,OA=OB=AB,
∴△OAB是等边三角形,即∠OAB=∠ABO=∠O=60°,
∴∠C=30°,∵四边形ADBC是⊙O的内接四边形,
∴∠D=180°﹣∠C=150°,∴弦AB所对的圆周角的度数为30°或150°.
故答案是:30°或150°.
分析:连接OA、OB,可得△OAB是等边三角形,根据圆周角定理和圆的内接四边形的性质定理,即可求解.
12.
考点:圆内接四边形的性质
解: 弧 的度数为 ,
,
四边形 内接于圆 ,
,
.
故答案为:
分析:由弧 的度数为 可求出 的度数,再根据圆的内接四边形的性质,即可求得 的度数,继而求得答案
13. 60°或120°
考点:圆周角定理,圆内接四边形的性质
解:如图,连接OA、OB.
弦AB将⊙O分为1:2两部分,
则∠AOB= ×360°=120°;
∴∠ACB= ∠AOB=60°,
∠ADB=180°﹣∠60=120°;
故这条弦所对的圆周角的度数为60°或120°.
故答案为:60°或120°
分析:此题有两种情况,连接OA、OB,由已知条件弦AB将⊙O分为1:2两部分,可求出∠AOB的度数,再利用圆周角定理求出∠ACB的度数,然后利用圆内接四边形的对角互补,就可求出∠ADB的度数。
14. 46°
考点:圆内接四边形的性质
解:∵OC∥AD, ∴∠OCD=180°-∠ADC=74°, ∵四边形ABCD内接于⊙O, ∴∠BCD=180°-∠DAB=120°, ∴∠OCD=∠BCD-∠OCD=46°,故答案为:46.
分析:根据平行线的性质求出∠OCD,根据圆内接四边形的性质求出∠BCD,计算即可.
15.
考点:圆周角定理,圆内接四边形的性质
解:连接AC,如图,
∵BA平分∠DBE,
∴∠ABE=∠ABD,
∵∠ABE=∠CDA,∠ABD=∠ACD,
∴∠ACD=∠CDA,
∴AC=AD=5,
∵AE⊥CB,
∴∠AEC=90°,
故答案为:2 .
分析:连接AC,由圆内接四边形的性质和圆周角定理得到∠BAE=∠CDA,∠ABD=∠ACD,从而得到∠ACD=∠CDA,得出AC=AD=5,然后利用勾股定理计算AE的长.
三、解答题
16. (1)解:∠E=∠F,∵∠DCE=∠BCF,∴∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,∴∠ADC=∠ABC.
(2)解:由(1)知∠ADC=∠ABC,∵∠EDC=∠ABC,∴∠EDC=∠ADC,∴∠ADC=90°,∴∠A=90°﹣42°=48°
(3)解:连结EF,如图,∵四边形ABCD为圆的内接四边形,∴∠ECD=∠A,∵∠ECD=∠1+∠2,∴∠A=∠1+∠2,∵∠A+∠1+∠2+∠E+∠F=180°,∴2∠A+α+β=180°,∴∠A=90°﹣ .
考点:圆内接四边形的性质
分析:(1)由三角形外角知识可得∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,再由∠E=∠F,∠EDC=∠ABC,等量代换可得∠ADC=∠ABC。
(2)由(1)知∠ADC=∠ABC,再由∠EDC=∠ABC,等量代换得出∠EDC=∠ADC,最后得出∠A。
(3)连结EF,由四边形ABCD为圆的内接四边形,可得∠ECD=∠A,再由三角形外角可得∠ECD=∠1+∠2,等量代换得出∠A=∠1+∠2,最后由三角形内角和定理可得∠A+∠1+∠2+∠E+∠F=180°,等量代换得出∠A的度数? .
17. (1)解:作 于 ,
∵ ,
∴ ,
∵ ,
∴ ;
(2)解:连接 ,
∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ .
考点:勾股定理,圆内接四边形的性质,等腰直角三角形
分析:(1)作OM⊥AC于M,根据等腰直角三角形的性质得到AM=CM=2 ,根据勾股定理即可得到结论;(2)连接OA,根据等腰直角三角形的性质得到∠MOC=∠MCO=45°,求得∠AOC=90°,根据圆内接四边形的性质即可得到结论.
18. (1)证明:连结AC,BD,
∴∠CAD=∠CBD,∠ABD=∠ACD,∠ADB=∠ACB,∠BAC=∠BDC,
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠CAD+∠BAC+∠ABD+∠CBD+∠ACB+∠ACD+∠ADB+∠BDC=360°,
∴∠CAD+∠BAC+∠ACB+∠ACD=180°,
即∠BAD+∠BCD=180°,
又∵∠DCE+∠BCD=180°,
∴∠BAD=∠DCE.
(2)解:①设BC与⊙O交于点E,连结DE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BED=∠CDE+∠BCD,
∴∠BED>∠BCD,
∴∠A+∠BCD<180°.
②延长DC交⊙O于点E,连结BE,
∵四边形ABED是⊙O的内接四边形,
∴∠A+∠BED=180°,
又∵∠BCD=∠CBE+∠BED,
∴∠BCD>∠BED,
∴∠A+∠BCD>180°.
考点:圆内接四边形的性质
分析:(1)连结AC,BD,由同弧所对的圆周角相等和四边形的内角和为360°,即可得证∠A+∠BCD=180°,再由同角的补角相等可得∠DCE=∠A.
(2)①设BC与⊙O交于点E,连结DE,根据圆的内接四边形对角互补和三角形外角性质,即可得证.
②延长DC交⊙O于点E,连结BE,根据圆的内接四边形对角互补和三角形外角性质,即可得证.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
