1.5 三角形全等的判定培优精选试题(含解析)
文档属性
| 名称 | 1.5 三角形全等的判定培优精选试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 08:13:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.5全等三角形的判定
一.选择题(共16小题)
1.(2019秋?平山县期末)我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
2.(2020春?揭西县期末)如图,AD=BC,∠DAB=∠CBA,由此可得下列哪组三角形全等( )
A.△ABC≌△BAD B.△AOC≌△AOB
C.△BOD≌△AOB D.没有三角形全等
3.(2020春?文圣区期末)已知:如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论:①∠EAB=∠FAC;②AF=AC;③FA平分∠EFC;④∠BFE=∠FAC中,正确的有( )个.
A.1 B.2 C.3 D.4
4.(2020春?碑林区校级期末)如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5 B.6 C.7 D.8
5.(2020春?吴中区期末)如图,已知AB⊥CD,AB=CD,E、F是AD上的两个点,CE⊥AD,BF⊥AD,若AD=a,BF=b,CE=c,则EF的长为( )
A.a+b﹣c B.b+c﹣a C.a+c﹣b D.a﹣b
6.(2020?毕节市)如图,在一个宽度为AB长的小巷内,一个梯子的长为a,梯子的底端位于AB上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到AB的距离BC为b,梯子的倾斜角∠BPC为45°;将该梯子的顶端放于另一侧墙上的点D处,点D到AB的距离AD为c,且此时梯子的倾斜角∠APD为75°,则AB的长等于( )
A.a B.b C. D.c
7.(2020春?太仓市期末)如图,△DEF的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(重合的除外)的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
8.(2020?鄂州)如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
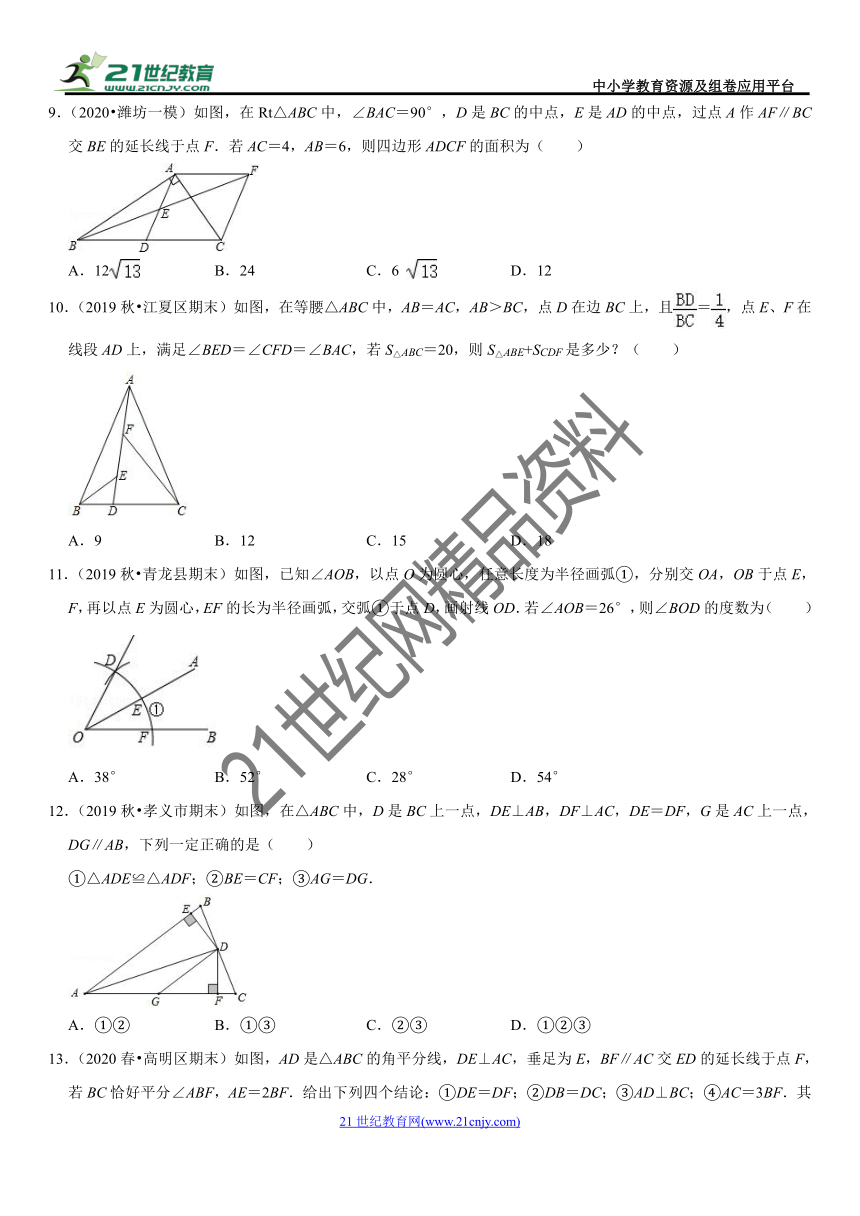
9.(2020?潍坊一模)如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.若AC=4,AB=6,则四边形ADCF的面积为( )
A.12 B.24 C.6 D.12
10.(2019秋?江夏区期末)如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+SCDF是多少?( )
A.9 B.12 C.15 D.18
11.(2019秋?青龙县期末)如图,已知∠AOB,以点O为圆心,任意长度为半径画弧①,分别交OA,OB于点E,F,再以点E为圆心,EF的长为半径画弧,交弧①于点D,画射线OD.若∠AOB=26°,则∠BOD的度数为( )
A.38° B.52° C.28° D.54°
12.(2019秋?孝义市期末)如图,在△ABC中,D是BC上一点,DE⊥AB,DF⊥AC,DE=DF,G是AC上一点,DG∥AB,下列一定正确的是( )
①△ADE≌△ADF;②BE=CF;③AG=DG.
A.①② B.①③ C.②③ D.①②③
13.(2020春?高明区期末)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论为( )
A.①②③ B.①②④ C.②③④ D.①②③④
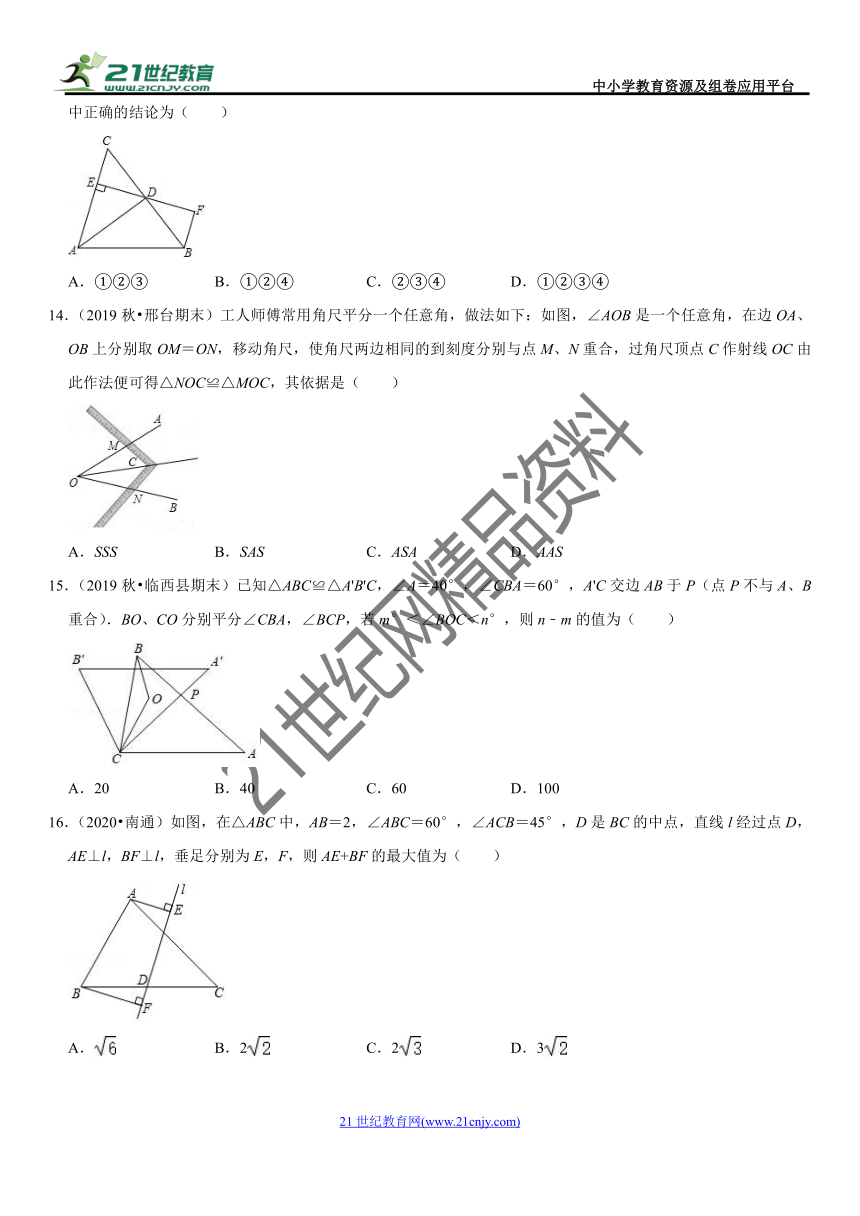
14.(2019秋?邢台期末)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
15.(2019秋?临西县期末)已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
16.(2020?南通)如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
二.解答题(共9小题)
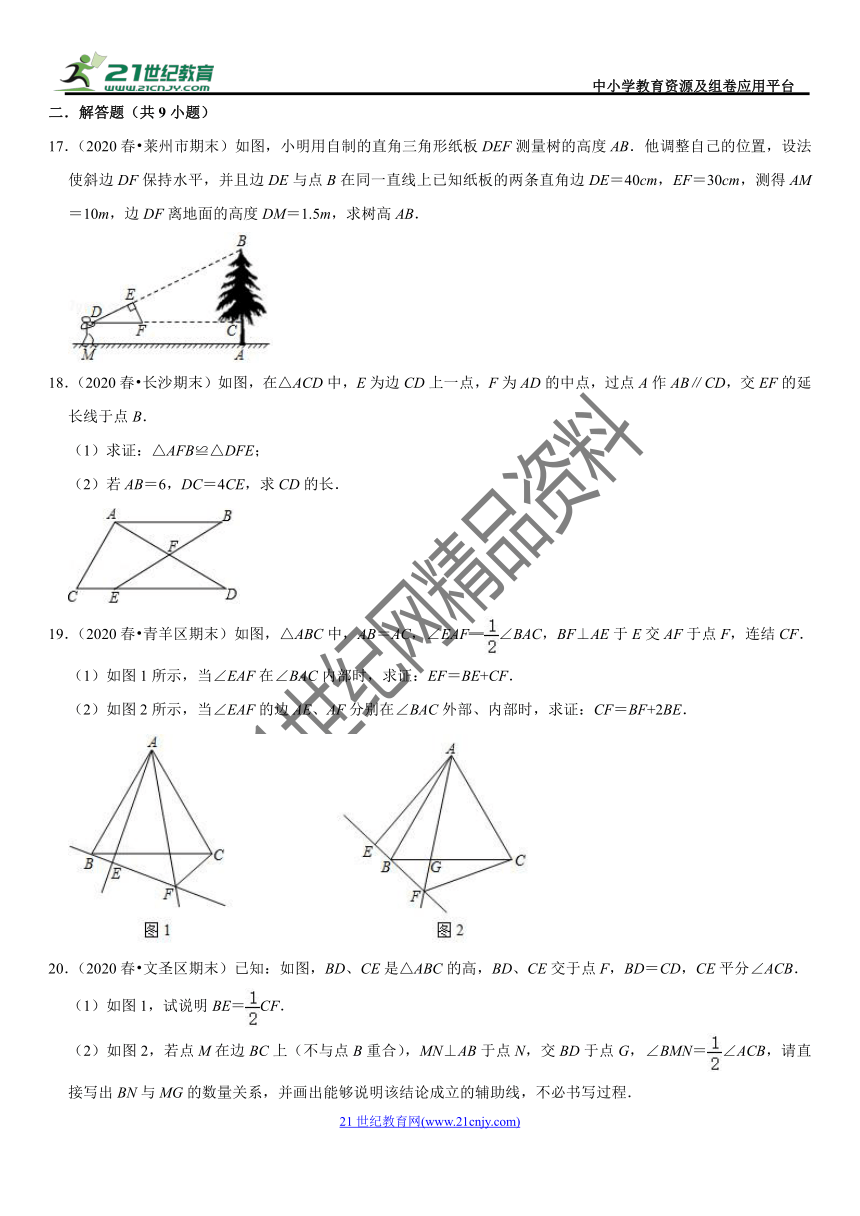
17.(2020春?莱州市期末)如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上已知纸板的两条直角边DE=40cm,EF=30cm,测得AM=10m,边DF离地面的高度DM=1.5m,求树高AB.
18.(2020春?长沙期末)如图,在△ACD中,E为边CD上一点,F为AD的中点,过点A作AB∥CD,交EF的延长线于点B.
(1)求证:△AFB≌△DFE;
(2)若AB=6,DC=4CE,求CD的长.
19.(2020春?青羊区期末)如图,△ABC中,AB=AC,∠EAF═∠BAC,BF⊥AE于E交AF于点F,连结CF.
(1)如图1所示,当∠EAF在∠BAC内部时,求证:EF=BE+CF.
(2)如图2所示,当∠EAF的边AE、AF分别在∠BAC外部、内部时,求证:CF=BF+2BE.
20.(2020春?文圣区期末)已知:如图,BD、CE是△ABC的高,BD、CE交于点F,BD=CD,CE平分∠ACB.
(1)如图1,试说明BE=CF.
(2)如图2,若点M在边BC上(不与点B重合),MN⊥AB于点N,交BD于点G,∠BMN=∠ACB,请直接写出BN与MG的数量关系,并画出能够说明该结论成立的辅助线,不必书写过程.
21.(2020春?沙坪坝区校级月考)如图,CD∥AB,△ABC的中线AE的延长线与CD交于点D.
(1)若AE=3,求DE的长度;
(2)∠DAC的平分线与DC交于点F,连接EF,若AF=DF,AC=DE,求证:AB=AF+EF.
22.(2020春?南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
23.(2020春?龙岗区期末)如图,点O为线段AB上的任意一点(不于A、B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC交于点P,AD交CO于点M,BC交DO于点N.
(1)试说明:CB=AD;
(2)若∠COD=70°,求∠APB的度数.
24.(2020?五华区二模)如图所示,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交BA、BC于点M、N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.请你观察图形,解答下列问题:
(1)求证:△ABC≌△DBC;
(2)若∠A=100°,∠E=50°,求∠ACB的度数.
25.(2020?扬中市模拟)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
三.填空题(共9小题)
26.(2020春?碑林区校级期末)如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为 m.
27.(2020春?三明期末)如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD.再作出BF的垂线DE,使A、C、E三点在一条直线上,通过证明△ABC≌△DEC,得到DE的长就等于AB的长,这里证明三角形全等的依据是 .
28.(2020春?彭州市期末)两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= cm.
29.(2019秋?松滋市期末)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
30.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
31.(2020春?市中区校级期末)如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=50°,则∠DFE= .
32.(2020春?迁西县期末)如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为4和9,则n的面积为 .
33.(2020春?福田区期中)如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有 .(填上所有正确结论的序号)
1.5全等三角形的判定
参考答案与试题解析
一.选择题(共16小题)
1.(2019秋?平山县期末)我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
【解答】解:根据伞的结构,AE=AF,伞骨DE=DF,AD是公共边,
∵在△ADE和△ADF中,
,
∴△ADE≌△ADF(SSS),
∴∠DAE=∠DAF,
即AP平分∠BAC.
故选:A.
2.(2020春?揭西县期末)如图,AD=BC,∠DAB=∠CBA,由此可得下列哪组三角形全等( )
A.△ABC≌△BAD B.△AOC≌△AOB
C.△BOD≌△AOB D.没有三角形全等
【解答】解:∵在△DAB和△CBA中
,
∴△DAB≌△CBA(SAS),
故选:A.
3.(2020春?文圣区期末)已知:如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论:①∠EAB=∠FAC;②AF=AC;③FA平分∠EFC;④∠BFE=∠FAC中,正确的有( )个.
A.1 B.2 C.3 D.4
【解答】解:在△AEF和△ABC中,
,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,∠C=∠EFA,
∴∠EAB=∠FAC,∠AFC=∠C,
∴∠EFA=∠AFC,
即FA平分∠EFC.
又∵∠AFB=∠C+∠FAC=∠AFE+∠BFE,
∴∠BFE=∠FAC.
故①②③④正确.
故选:D.
4.(2020春?碑林区校级期末)如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5 B.6 C.7 D.8
【解答】解:∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,∠BAC=∠DCA,
在△ABD和△CDB中,,
∴△ABD≌△CDB(ASA),
同理:△ABC≌△CDA(ASA);
∴AB=CD,BC=DA,
在△AOB和△COD中,,
∴△AOB≌△COD(AAS),
同理:△AOD≌△COB(AAS);
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AEO=∠CFD=∠CFO=90°,
在△ABE和△CDF中,,
∴△ABE≌△CDF(AAS),
同理:△AOE≌△COF(AAS),△ADE≌△CBF(AAS);
图中共有7对全等三角形;
故选:C.
5.(2020春?吴中区期末)如图,已知AB⊥CD,AB=CD,E、F是AD上的两个点,CE⊥AD,BF⊥AD,若AD=a,BF=b,CE=c,则EF的长为( )
A.a+b﹣c B.b+c﹣a C.a+c﹣b D.a﹣b
【解答】解:∵AB⊥CD,CE⊥AD,
∴∠C+∠D=90°,∠A+∠D=90°,
∴∠A=∠C,且AB=CD,∠AFB=∠CED,
∴△ABF≌△CDE(AAS),
∴BF=DE=b,CE=AF=c,
∵AE=AD﹣DE=a﹣b,
∴EF=AF﹣AE=c﹣(a﹣b)=c﹣a+b,
故选:B.
6.(2020?毕节市)如图,在一个宽度为AB长的小巷内,一个梯子的长为a,梯子的底端位于AB上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到AB的距离BC为b,梯子的倾斜角∠BPC为45°;将该梯子的顶端放于另一侧墙上的点D处,点D到AB的距离AD为c,且此时梯子的倾斜角∠APD为75°,则AB的长等于( )
A.a B.b C. D.c
【解答】解:过点C作CE⊥AD于E,如图所示:
则四边形ABCE是矩形,
∴AB=CE,∠CED=∠DAP=90°,
∵∠BPC=45°,∠APD=75°,
∴∠CPD=180°﹣45°﹣75°=60°,
∵CP=DP=a,
∴△CPD是等边三角形,
∴CD=DP,∠PDC=60°,
∵∠ADP=90°﹣75°=15°,
∴∠EDC=15°+60°=75°,
∴∠EDC=∠APD,
在△EDC和△APD中,
,
∴△EDC≌△APD(AAS),
∴CE=AD,
∴AB=AD=c,
故选:D.
7.(2020春?太仓市期末)如图,△DEF的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(重合的除外)的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
【解答】解:如图所示可作3个全等的三角形.
故选:C.
8.(2020?鄂州)如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
【解答】解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,故②正确;
∵∠OAC=∠OBD,
由三角形的外角性质得:
∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°,故①正确;
作OG⊥AM于G,OH⊥DM于H,如图所示,
则∠OGA=∠OHB=90°,
∵△AOC≌△BOD,
∴OG=OH,
∴OM平分∠AMD,故④正确;
假设OM平分∠AOD,则∠DOM=∠AOM,
在△AMO与△DMO中,
,
∴△AMO≌△OMD(ASA),
∴AO=OD,
∵OC=OD,
∴OA=OC,
而OA<OC,故③错误;
正确的个数有3个;
故选:B.
9.(2020?潍坊一模)如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.若AC=4,AB=6,则四边形ADCF的面积为( )
A.12 B.24 C.6 D.12
【解答】解:∵AF∥BC,
∴∠AFB=∠DBF,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∵AF∥BC,
∴△AFC的面积=△ABD的面积,
∴四边形ADCF的面积=△ADC的面积+△AFC的面积
=△ADC的面积+△ABD的面积
=△ABC的面积
=×4×6
=12,
故选:D.
10.(2019秋?江夏区期末)如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+SCDF是多少?( )
A.9 B.12 C.15 D.18
【解答】解:∵∠BED=∠CFD=∠BAC,∠BED=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠CFD=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
∵,
∴△ABE≌△CAF(ASA),
∴S△ABE=S△ACF,
∴S△ABE+SCDF=S△ACD
∵S△ABC=20,=,
∴S△ACD=15,
故选:C.
11.(2019秋?青龙县期末)如图,已知∠AOB,以点O为圆心,任意长度为半径画弧①,分别交OA,OB于点E,F,再以点E为圆心,EF的长为半径画弧,交弧①于点D,画射线OD.若∠AOB=26°,则∠BOD的度数为( )
A.38° B.52° C.28° D.54°
【解答】解:由作图可知,OD=OE=OF,EF=DE,
∴△ODE≌△OFE(SSS),
∴∠EOD=∠EOF=26°,
∴∠BOD=2∠AOB=52°,
故选:B.
12.(2019秋?孝义市期末)如图,在△ABC中,D是BC上一点,DE⊥AB,DF⊥AC,DE=DF,G是AC上一点,DG∥AB,下列一定正确的是( )
①△ADE≌△ADF;②BE=CF;③AG=DG.
A.①② B.①③ C.②③ D.①②③
【解答】解:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∵DE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF(HL),故①正确;
∴∠DAE=∠DAF,
∵DG∥AB,
∴∠DAE=∠ADG,
∴∠DAF=∠ADG,
∴AG=DG,故③正确,
由条件无法证明BE=CF,故②错误,
故选:B.
13.(2020春?高明区期末)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论为( )
A.①②③ B.①②④ C.②③④ D.①②③④
【解答】解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
又∵AD=AD,
∴△ABD≌△ACD(AAS),
∴BD=CD,故②正确,
∠ADB=∠ADC=90°,
∴AD⊥BC,故③正确,
在△CDE与△DBF中,
,
∴△CDE≌△DBF(ASA),
∴DE=DF,CE=BF,故①正确,
∵AE=2BF,
∴AE=2CE,
∴AC=AE+CE=3CE=3BF,故④正确;
故选:D.
14.(2019秋?邢台期末)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
【解答】解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
15.(2019秋?临西县期末)已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
【解答】解:∵BO、CO分别平分∠ABC、∠PCB,
∴∠OBC=∠ABC,∠OCB=∠PCB,
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(∠ABC+∠PCB),
=180°﹣(180°﹣∠BPC),
=90°+∠BPC=90°+(∠A+∠ACP),
=110°+∠ACP,
∵∠A=40°,∠CBA=60°,
∴∠ACB=180°﹣∠A﹣∠CBA=180°﹣40°﹣60°=80°,
∵P点在AB边上且不与A、B重合,
∴0°<∠ACP<80°,
∴0°<2∠BOC﹣220°<80°,
∴110°<∠BOC<150°,
∴m=110,n=150.
∴n﹣m=40.
故选:B.
16.(2020?南通)如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
【解答】解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,
在Rt△AHB中,
∵∠ABC=60°,AB=2,
∴BH=1,AH=,
在Rt△AHC中,∠ACB=45°,
∴AC===,
∵点D为BC中点,
∴BD=CD,
在△BFD与△CKD中,
,
∴△BFD≌△CKD(AAS),
∴BF=CK,
延长AE,过点C作CN⊥AE于点N,
可得AE+BF=AE+CK=AE+EN=AN,
在Rt△ACN中,AN<AC,
当直线l⊥AC时,最大值为,
综上所述,AE+BF的最大值为.
故选:A.
二.解答题(共9小题)
17.(2020春?莱州市期末)如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上已知纸板的两条直角边DE=40cm,EF=30cm,测得AM=10m,边DF离地面的高度DM=1.5m,求树高AB.
【解答】解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米,
∴树高为9米.
18.(2020春?长沙期末)如图,在△ACD中,E为边CD上一点,F为AD的中点,过点A作AB∥CD,交EF的延长线于点B.
(1)求证:△AFB≌△DFE;
(2)若AB=6,DC=4CE,求CD的长.
【解答】(1)证明:∵AB∥CD,
∴∠ABF=∠DEF,∠BAF=∠D,
∵F为AD的中点,
∴AF=DF,
在△AFB和△DFE中,
,
∴△AFB≌△DFE(AAS),
(2)∵△AFB≌△DFE,
∴AB=DE=6,
∵DC=4CE,
∴CE+6=4CE,
∴CE=2.
∴CD=CE+DE=2+6=8.
19.(2020春?青羊区期末)如图,△ABC中,AB=AC,∠EAF═∠BAC,BF⊥AE于E交AF于点F,连结CF.
(1)如图1所示,当∠EAF在∠BAC内部时,求证:EF=BE+CF.
(2)如图2所示,当∠EAF的边AE、AF分别在∠BAC外部、内部时,求证:CF=BF+2BE.
【解答】证明:(1)如图,在EF上截取EH=BE,连接AH,
∵EB=EH,AE⊥BF,
∴AB=AH,
∵AB=AH,AE⊥BH,
∴∠BAE=∠EAH,
∵AB=AD,
∴AC=AH,
∵∠EAF═∠BAC
∴∠BAE+∠CAF=∠EAF,
∴∠BAE+∠CAF=∠EAH+∠FAH,
∴∠CAF=∠HAF,
在△ACF和△AHF中,
,
∴△ACF≌△AHF(SAS),
∴CF=HF,
∴EF=EH+HF=BE+CF;
(2)如图,在BE的延长线上截取EN=BE,连接AN,
∵AE⊥BF,BE=EN,AB=AC,
∴AN=AB=AC,
∵AN=AB,AE⊥BN,
∴∠BAE=∠NAE,
∵∠EAF═∠BAC
∴∠EAF+∠NAE=(∠BAC+2∠NAE)
∴∠FAN=∠CAN,
∴∠FAN=∠CAF,
在△ACF和△ANF中,
,
∴△ACF≌△ANF(SAS),
∴CF=NF,
∴CF=BF+2BE.
20.(2020春?文圣区期末)已知:如图,BD、CE是△ABC的高,BD、CE交于点F,BD=CD,CE平分∠ACB.
(1)如图1,试说明BE=CF.
(2)如图2,若点M在边BC上(不与点B重合),MN⊥AB于点N,交BD于点G,∠BMN=∠ACB,请直接写出BN与MG的数量关系,并画出能够说明该结论成立的辅助线,不必书写过程.
【解答】解:(1)∵BD⊥AC,CE⊥AB,
∴∠ADB=∠BDC=∠AEC=90°,
∴∠A+∠ABD=90°,∠A+∠ACE=90°,
∴∠ABD=∠ACE,
在△ABD和△FCD中,
,
∴△ABD≌△FCD(SAS),
∴AB=CF,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
在△ACE和△BCE中,
,
∴△ACE≌△BCE(ASA),
∴AE=BE,
∴BE=AB=CF;
(2)BN=MG,
理由如下:如图,过点M作MH∥AC,交AB于H,交BD于P,
∵BD=CD,BD⊥CD,
∴∠DBC=∠DCB=45°,
∵MH∥AC,
∴∠PMB=∠DCB=∠PBM=45°,∠BPM=∠BDC=90°,
∴BP=PM,
∵∠BHP+∠HBP=90°,∠BHP+∠HMN=90°,
∴∠HBP=∠HMN,
在△BHP和△MGP中,
,
∴△BPH≌△MPG(ASA),
∴GM=BH,
∵∠BMN=∠ACB=22.5°,
∴∠BMN=∠HMN=22.5°,
在△BMN和△HMN中,
,
∴△BMN≌△HMN(ASA)
∴BN=NH,
∴BN=BH=MG.
21.(2020春?沙坪坝区校级月考)如图,CD∥AB,△ABC的中线AE的延长线与CD交于点D.
(1)若AE=3,求DE的长度;
(2)∠DAC的平分线与DC交于点F,连接EF,若AF=DF,AC=DE,求证:AB=AF+EF.
【解答】解:(1)∵CD∥AB,
∴∠B=∠DCE,
∵AE是中线,
∴CE=BE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(ASA),
∴AE=DE=3,
∴DE的长为3;
(2)∵△ABE≌△DCE,
∴AB=CD,
∵AF平分∠DAC,
∴∠CAF=∠DAF,
∵AC=DE,AE=DE,
∴AC=AE,
在△CAF和△EAF中,
,
∴△CAF≌△EAF(SAS),
∴CF=EF,
∴AB=CD=CF+DF=EF+AF.
22.(2020春?南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
【解答】解:(1)∵DB⊥AM,DC⊥AN,
∴∠DBE=∠DCF=90°,
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(AAS).
∴DE=DF;
(2)EF=FC+BE,
理由:过点D作∠CDG=∠BDE,交AN于点G,
在△BDE和△CDG中,
,
∴△BDE≌△CDG(ASA),
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
在△EDF和△GDF中,
,
∴△EDF≌△GDF(SAS).
∴EF=GF,
∴EF=FC+CG=FC+BE.
23.(2020春?龙岗区期末)如图,点O为线段AB上的任意一点(不于A、B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC交于点P,AD交CO于点M,BC交DO于点N.
(1)试说明:CB=AD;
(2)若∠COD=70°,求∠APB的度数.
【解答】证明:(1)∵∠AOC=∠BOD,
∴∠AOD=∠BOC,
又∵OA=OC,OB=OD,
∴△AOD≌△COB(SAS),
∴CB=AD;
(2)∵∠COD=70°,
∴∠AOC=∠BOD=55°,
∴∠AOD=∠COD+∠BOD=125°=∠BOC,
∵△AOD≌△COB,
∴∠BCO=∠DAO,
∴∠DAO+∠CBO=∠BCO+∠CBO,
∴180°﹣∠APB=180°﹣∠BOC,
∴∠APB=125°
24.(2020?五华区二模)如图所示,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交BA、BC于点M、N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.请你观察图形,解答下列问题:
(1)求证:△ABC≌△DBC;
(2)若∠A=100°,∠E=50°,求∠ACB的度数.
【解答】解:(1)如图所示,连接MN,NF,
由题可得,BM=BF,MN=FN,BN=BN,
∴△BMN≌△BFN(SSS),
∴∠ABC=∠DBC,
又∵AB=DB,BC=BC,
∴△ABC≌△DBC(SAS);
(2)∵∠A=100°,∠E=50°,
∴∠ABE=30°,
∴∠ABC=∠ABD=15°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣100°﹣15°=65°.
25.(2020?扬中市模拟)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
【解答】证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
,
∴△ABE≌△ACD(ASA),
∴AE=AD;
(2)解:∵∠ACB=65°,AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,
∵∠ABD=∠ACD,∠AOB=∠COD,
∴∠BDC=∠BAC=50°.
三.填空题(共9小题)
26.(2020春?碑林区校级期末)如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为 4 m.
【解答】解:∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE,
在△ABC和△DEF中,,
∴△ABC≌△DEF(AAS),
∴BC=EF,
∴BC﹣FC=EF﹣FC,
即BF=CE=5m,
∴FC=BE﹣BF﹣CE=14m﹣5m﹣5m=4m;
故答案为:4.
27.(2020春?三明期末)如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD.再作出BF的垂线DE,使A、C、E三点在一条直线上,通过证明△ABC≌△DEC,得到DE的长就等于AB的长,这里证明三角形全等的依据是 ASA .
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故答案为:ASA.
28.(2020春?彭州市期末)两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= 4 cm.
【解答】解:在Rt△OMP和Rt△ONP中,OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∵∠AOB=60°,
∴∠MOP=∠NOP=30°,
∵∠OMP=90°,
∴OP=2MP,OM=MP=6cm,
∴MP=2cm,
∴OP=4cm,
故答案为:4.
29.(2019秋?松滋市期末)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 20 cm.
【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
30.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 ③⑤⑥ .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
【解答】解:延长EB到G,使BG=DF,连接AG,
∵AB⊥CB,AD⊥CD,
∴∠D=∠ABG=90°,
在△ADF和△ABG中
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠G=∠DFA,∠DAF=∠BAG,
∵∠EAF=70°,∠DAB=140°,
∴∠DAF+∠EAB=∠DAB﹣∠FAE=140°﹣70°=70°,
∴∠EAG=∠EAB+∠BAG=∠EAB+∠FAD=70°,
∴∠FAE=∠EAG=70°,
在△FAE和△GAE中
,
∴△FAE≌△GAE(SAS),
∴∠FEA=∠GEA,∠G=∠EFA,EF=EG,
∴EF=EB+DF,∠FAE≠∠EAB,故⑤正确,④错误;
∴∠G=∠EFA=∠DFA,即AF平分∠DFE,故③正确;
∵CF+CE>EF,EF=DF+BE,
∴CF+CE>DF+BE,故⑥正确;
根据已知不能推出△ADF≌△ABE,故①错误,②错误;
故答案为:③⑤⑥.
31.(2020春?市中区校级期末)如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=50°,则∠DFE= 40° .
【解答】解:连接BD、AE,
∵DA⊥AB,FC⊥AB,
∴∠DAB=∠BCF=90°,
在△DAB和△BCF中,
,
∴△DAB≌△BCF(SAS),
∴BD=BF,∠ADB=∠ABF,
∴∠BDF=∠BFD,
∵∠DAB=90°,
∴∠ADB+∠DBA=90°,
∴∠DBF=∠ABD+∠ABF=90°,
∴∠BFD=∠BDF=45°,
同理∠AFE=45°,
∴∠DFE=45°+45°﹣50°=40°,
故答案为:40°.
32.(2020春?迁西县期末)如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为4和9,则n的面积为 13 .
【解答】解:由于m、q、n都是正方形,所以AC=CD,∠ACD=90°;
∵∠ACB+∠DCE=∠ACB+∠BAC=90°,
∴∠BAC=∠DCE,且AC=CD,∠ABC=∠DEC=90°
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sn=Sm+Sq=4+9=13,
∴正方形n的面积为13,
故答案为:13.
33.(2020春?福田区期中)如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有 ①②③④ .(填上所有正确结论的序号)
【解答】解:连接BO,如图1所示:
∵AB=AC,AD⊥BC,
∴BO=CO,
∴∠OBC=∠OCB,
又∵OP=OC,
∴OP=OB,
∴∠OBP=∠OPB,
又∵在等腰△ABC中∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠OBC+∠OBP=∠OCB+∠ACO,
∴∠OBP=∠ACO,
∴∠APO=∠ACO,故①正确;
又∵∠ABC=∠PBO+∠CBO=30°,
∴∠APO+∠DCO=30°,
∵∠PBC+∠BPC+∠BCP=180°,∠PBC=30°,
∴∠BPC+∠BCP=150°,
又∵∠BPC=∠APO+∠CPO,
∠BCP=∠BCO+∠PCO,
∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
又∵∠POC+∠OPC+∠OCP=180°,
∴∠POC=60°,
又∵OP=OC,
∴△OPC是等边三角形,
∴PC=PO,∠PCO=60°,故③正确;
∴∠APO+∠DCO+∠PCO=30°+60°,
即:∠APO+∠PCB=90°,故②正确;
在线段AC上截取AE=AP,连接PE,如图2所示:
∵∠BAC+∠CAP=180°,∠BAC=120°,
∴∠CAP=60°,
∴△APE是等边三角形,
∴AP=EP,
又∵△OPC是等边三角形,
∴OP=CP,
又∵∠APE=∠APO+∠OPE=60°,
∠CPO=∠CPE+∠OPE=60°,
∴∠APO=∠EPC,
在△APO和△EPC中,,
∴△APO≌△EPC(SAS),
∴AO=EC,
又∵AC=AE+EC,AE=AP,
∴AO+AP=AC,故④正确;
故答案为:①②③④.
_21?????????è?????(www.21cnjy.com)_
1.5全等三角形的判定
一.选择题(共16小题)
1.(2019秋?平山县期末)我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
2.(2020春?揭西县期末)如图,AD=BC,∠DAB=∠CBA,由此可得下列哪组三角形全等( )
A.△ABC≌△BAD B.△AOC≌△AOB
C.△BOD≌△AOB D.没有三角形全等
3.(2020春?文圣区期末)已知:如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论:①∠EAB=∠FAC;②AF=AC;③FA平分∠EFC;④∠BFE=∠FAC中,正确的有( )个.
A.1 B.2 C.3 D.4
4.(2020春?碑林区校级期末)如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5 B.6 C.7 D.8
5.(2020春?吴中区期末)如图,已知AB⊥CD,AB=CD,E、F是AD上的两个点,CE⊥AD,BF⊥AD,若AD=a,BF=b,CE=c,则EF的长为( )
A.a+b﹣c B.b+c﹣a C.a+c﹣b D.a﹣b
6.(2020?毕节市)如图,在一个宽度为AB长的小巷内,一个梯子的长为a,梯子的底端位于AB上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到AB的距离BC为b,梯子的倾斜角∠BPC为45°;将该梯子的顶端放于另一侧墙上的点D处,点D到AB的距离AD为c,且此时梯子的倾斜角∠APD为75°,则AB的长等于( )
A.a B.b C. D.c
7.(2020春?太仓市期末)如图,△DEF的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(重合的除外)的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
8.(2020?鄂州)如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
9.(2020?潍坊一模)如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.若AC=4,AB=6,则四边形ADCF的面积为( )
A.12 B.24 C.6 D.12
10.(2019秋?江夏区期末)如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+SCDF是多少?( )
A.9 B.12 C.15 D.18
11.(2019秋?青龙县期末)如图,已知∠AOB,以点O为圆心,任意长度为半径画弧①,分别交OA,OB于点E,F,再以点E为圆心,EF的长为半径画弧,交弧①于点D,画射线OD.若∠AOB=26°,则∠BOD的度数为( )
A.38° B.52° C.28° D.54°
12.(2019秋?孝义市期末)如图,在△ABC中,D是BC上一点,DE⊥AB,DF⊥AC,DE=DF,G是AC上一点,DG∥AB,下列一定正确的是( )
①△ADE≌△ADF;②BE=CF;③AG=DG.
A.①② B.①③ C.②③ D.①②③
13.(2020春?高明区期末)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论为( )
A.①②③ B.①②④ C.②③④ D.①②③④
14.(2019秋?邢台期末)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
15.(2019秋?临西县期末)已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
16.(2020?南通)如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
二.解答题(共9小题)
17.(2020春?莱州市期末)如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上已知纸板的两条直角边DE=40cm,EF=30cm,测得AM=10m,边DF离地面的高度DM=1.5m,求树高AB.
18.(2020春?长沙期末)如图,在△ACD中,E为边CD上一点,F为AD的中点,过点A作AB∥CD,交EF的延长线于点B.
(1)求证:△AFB≌△DFE;
(2)若AB=6,DC=4CE,求CD的长.
19.(2020春?青羊区期末)如图,△ABC中,AB=AC,∠EAF═∠BAC,BF⊥AE于E交AF于点F,连结CF.
(1)如图1所示,当∠EAF在∠BAC内部时,求证:EF=BE+CF.
(2)如图2所示,当∠EAF的边AE、AF分别在∠BAC外部、内部时,求证:CF=BF+2BE.
20.(2020春?文圣区期末)已知:如图,BD、CE是△ABC的高,BD、CE交于点F,BD=CD,CE平分∠ACB.
(1)如图1,试说明BE=CF.
(2)如图2,若点M在边BC上(不与点B重合),MN⊥AB于点N,交BD于点G,∠BMN=∠ACB,请直接写出BN与MG的数量关系,并画出能够说明该结论成立的辅助线,不必书写过程.
21.(2020春?沙坪坝区校级月考)如图,CD∥AB,△ABC的中线AE的延长线与CD交于点D.
(1)若AE=3,求DE的长度;
(2)∠DAC的平分线与DC交于点F,连接EF,若AF=DF,AC=DE,求证:AB=AF+EF.
22.(2020春?南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
23.(2020春?龙岗区期末)如图,点O为线段AB上的任意一点(不于A、B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC交于点P,AD交CO于点M,BC交DO于点N.
(1)试说明:CB=AD;
(2)若∠COD=70°,求∠APB的度数.
24.(2020?五华区二模)如图所示,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交BA、BC于点M、N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.请你观察图形,解答下列问题:
(1)求证:△ABC≌△DBC;
(2)若∠A=100°,∠E=50°,求∠ACB的度数.
25.(2020?扬中市模拟)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
三.填空题(共9小题)
26.(2020春?碑林区校级期末)如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为 m.
27.(2020春?三明期末)如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD.再作出BF的垂线DE,使A、C、E三点在一条直线上,通过证明△ABC≌△DEC,得到DE的长就等于AB的长,这里证明三角形全等的依据是 .
28.(2020春?彭州市期末)两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= cm.
29.(2019秋?松滋市期末)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
30.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
31.(2020春?市中区校级期末)如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=50°,则∠DFE= .
32.(2020春?迁西县期末)如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为4和9,则n的面积为 .
33.(2020春?福田区期中)如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有 .(填上所有正确结论的序号)
1.5全等三角形的判定
参考答案与试题解析
一.选择题(共16小题)
1.(2019秋?平山县期末)我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
【解答】解:根据伞的结构,AE=AF,伞骨DE=DF,AD是公共边,
∵在△ADE和△ADF中,
,
∴△ADE≌△ADF(SSS),
∴∠DAE=∠DAF,
即AP平分∠BAC.
故选:A.
2.(2020春?揭西县期末)如图,AD=BC,∠DAB=∠CBA,由此可得下列哪组三角形全等( )
A.△ABC≌△BAD B.△AOC≌△AOB
C.△BOD≌△AOB D.没有三角形全等
【解答】解:∵在△DAB和△CBA中
,
∴△DAB≌△CBA(SAS),
故选:A.
3.(2020春?文圣区期末)已知:如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论:①∠EAB=∠FAC;②AF=AC;③FA平分∠EFC;④∠BFE=∠FAC中,正确的有( )个.
A.1 B.2 C.3 D.4
【解答】解:在△AEF和△ABC中,
,
∴△AEF≌△ABC(SAS),
∴∠EAF=∠BAC,AF=AC,∠C=∠EFA,
∴∠EAB=∠FAC,∠AFC=∠C,
∴∠EFA=∠AFC,
即FA平分∠EFC.
又∵∠AFB=∠C+∠FAC=∠AFE+∠BFE,
∴∠BFE=∠FAC.
故①②③④正确.
故选:D.
4.(2020春?碑林区校级期末)如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5 B.6 C.7 D.8
【解答】解:∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,∠BAC=∠DCA,
在△ABD和△CDB中,,
∴△ABD≌△CDB(ASA),
同理:△ABC≌△CDA(ASA);
∴AB=CD,BC=DA,
在△AOB和△COD中,,
∴△AOB≌△COD(AAS),
同理:△AOD≌△COB(AAS);
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AEO=∠CFD=∠CFO=90°,
在△ABE和△CDF中,,
∴△ABE≌△CDF(AAS),
同理:△AOE≌△COF(AAS),△ADE≌△CBF(AAS);
图中共有7对全等三角形;
故选:C.
5.(2020春?吴中区期末)如图,已知AB⊥CD,AB=CD,E、F是AD上的两个点,CE⊥AD,BF⊥AD,若AD=a,BF=b,CE=c,则EF的长为( )
A.a+b﹣c B.b+c﹣a C.a+c﹣b D.a﹣b
【解答】解:∵AB⊥CD,CE⊥AD,
∴∠C+∠D=90°,∠A+∠D=90°,
∴∠A=∠C,且AB=CD,∠AFB=∠CED,
∴△ABF≌△CDE(AAS),
∴BF=DE=b,CE=AF=c,
∵AE=AD﹣DE=a﹣b,
∴EF=AF﹣AE=c﹣(a﹣b)=c﹣a+b,
故选:B.
6.(2020?毕节市)如图,在一个宽度为AB长的小巷内,一个梯子的长为a,梯子的底端位于AB上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到AB的距离BC为b,梯子的倾斜角∠BPC为45°;将该梯子的顶端放于另一侧墙上的点D处,点D到AB的距离AD为c,且此时梯子的倾斜角∠APD为75°,则AB的长等于( )
A.a B.b C. D.c
【解答】解:过点C作CE⊥AD于E,如图所示:
则四边形ABCE是矩形,
∴AB=CE,∠CED=∠DAP=90°,
∵∠BPC=45°,∠APD=75°,
∴∠CPD=180°﹣45°﹣75°=60°,
∵CP=DP=a,
∴△CPD是等边三角形,
∴CD=DP,∠PDC=60°,
∵∠ADP=90°﹣75°=15°,
∴∠EDC=15°+60°=75°,
∴∠EDC=∠APD,
在△EDC和△APD中,
,
∴△EDC≌△APD(AAS),
∴CE=AD,
∴AB=AD=c,
故选:D.
7.(2020春?太仓市期末)如图,△DEF的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形,选取图中三个格点组成三角形,能与△DEF全等(重合的除外)的三角形个数为( )
A.1个 B.2个 C.3个 D.4个
【解答】解:如图所示可作3个全等的三角形.
故选:C.
8.(2020?鄂州)如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
【解答】解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,故②正确;
∵∠OAC=∠OBD,
由三角形的外角性质得:
∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°,故①正确;
作OG⊥AM于G,OH⊥DM于H,如图所示,
则∠OGA=∠OHB=90°,
∵△AOC≌△BOD,
∴OG=OH,
∴OM平分∠AMD,故④正确;
假设OM平分∠AOD,则∠DOM=∠AOM,
在△AMO与△DMO中,
,
∴△AMO≌△OMD(ASA),
∴AO=OD,
∵OC=OD,
∴OA=OC,
而OA<OC,故③错误;
正确的个数有3个;
故选:B.
9.(2020?潍坊一模)如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.若AC=4,AB=6,则四边形ADCF的面积为( )
A.12 B.24 C.6 D.12
【解答】解:∵AF∥BC,
∴∠AFB=∠DBF,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∵AF∥BC,
∴△AFC的面积=△ABD的面积,
∴四边形ADCF的面积=△ADC的面积+△AFC的面积
=△ADC的面积+△ABD的面积
=△ABC的面积
=×4×6
=12,
故选:D.
10.(2019秋?江夏区期末)如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+SCDF是多少?( )
A.9 B.12 C.15 D.18
【解答】解:∵∠BED=∠CFD=∠BAC,∠BED=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠CFD=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
∵,
∴△ABE≌△CAF(ASA),
∴S△ABE=S△ACF,
∴S△ABE+SCDF=S△ACD
∵S△ABC=20,=,
∴S△ACD=15,
故选:C.
11.(2019秋?青龙县期末)如图,已知∠AOB,以点O为圆心,任意长度为半径画弧①,分别交OA,OB于点E,F,再以点E为圆心,EF的长为半径画弧,交弧①于点D,画射线OD.若∠AOB=26°,则∠BOD的度数为( )
A.38° B.52° C.28° D.54°
【解答】解:由作图可知,OD=OE=OF,EF=DE,
∴△ODE≌△OFE(SSS),
∴∠EOD=∠EOF=26°,
∴∠BOD=2∠AOB=52°,
故选:B.
12.(2019秋?孝义市期末)如图,在△ABC中,D是BC上一点,DE⊥AB,DF⊥AC,DE=DF,G是AC上一点,DG∥AB,下列一定正确的是( )
①△ADE≌△ADF;②BE=CF;③AG=DG.
A.①② B.①③ C.②③ D.①②③
【解答】解:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∵DE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF(HL),故①正确;
∴∠DAE=∠DAF,
∵DG∥AB,
∴∠DAE=∠ADG,
∴∠DAF=∠ADG,
∴AG=DG,故③正确,
由条件无法证明BE=CF,故②错误,
故选:B.
13.(2020春?高明区期末)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论为( )
A.①②③ B.①②④ C.②③④ D.①②③④
【解答】解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
又∵AD=AD,
∴△ABD≌△ACD(AAS),
∴BD=CD,故②正确,
∠ADB=∠ADC=90°,
∴AD⊥BC,故③正确,
在△CDE与△DBF中,
,
∴△CDE≌△DBF(ASA),
∴DE=DF,CE=BF,故①正确,
∵AE=2BF,
∴AE=2CE,
∴AC=AE+CE=3CE=3BF,故④正确;
故选:D.
14.(2019秋?邢台期末)工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的到刻度分别与点M、N重合,过角尺顶点C作射线OC由此作法便可得△NOC≌△MOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
【解答】解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
15.(2019秋?临西县期末)已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20 B.40 C.60 D.100
【解答】解:∵BO、CO分别平分∠ABC、∠PCB,
∴∠OBC=∠ABC,∠OCB=∠PCB,
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(∠ABC+∠PCB),
=180°﹣(180°﹣∠BPC),
=90°+∠BPC=90°+(∠A+∠ACP),
=110°+∠ACP,
∵∠A=40°,∠CBA=60°,
∴∠ACB=180°﹣∠A﹣∠CBA=180°﹣40°﹣60°=80°,
∵P点在AB边上且不与A、B重合,
∴0°<∠ACP<80°,
∴0°<2∠BOC﹣220°<80°,
∴110°<∠BOC<150°,
∴m=110,n=150.
∴n﹣m=40.
故选:B.
16.(2020?南通)如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
【解答】解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,
在Rt△AHB中,
∵∠ABC=60°,AB=2,
∴BH=1,AH=,
在Rt△AHC中,∠ACB=45°,
∴AC===,
∵点D为BC中点,
∴BD=CD,
在△BFD与△CKD中,
,
∴△BFD≌△CKD(AAS),
∴BF=CK,
延长AE,过点C作CN⊥AE于点N,
可得AE+BF=AE+CK=AE+EN=AN,
在Rt△ACN中,AN<AC,
当直线l⊥AC时,最大值为,
综上所述,AE+BF的最大值为.
故选:A.
二.解答题(共9小题)
17.(2020春?莱州市期末)如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上已知纸板的两条直角边DE=40cm,EF=30cm,测得AM=10m,边DF离地面的高度DM=1.5m,求树高AB.
【解答】解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米,
∴树高为9米.
18.(2020春?长沙期末)如图,在△ACD中,E为边CD上一点,F为AD的中点,过点A作AB∥CD,交EF的延长线于点B.
(1)求证:△AFB≌△DFE;
(2)若AB=6,DC=4CE,求CD的长.
【解答】(1)证明:∵AB∥CD,
∴∠ABF=∠DEF,∠BAF=∠D,
∵F为AD的中点,
∴AF=DF,
在△AFB和△DFE中,
,
∴△AFB≌△DFE(AAS),
(2)∵△AFB≌△DFE,
∴AB=DE=6,
∵DC=4CE,
∴CE+6=4CE,
∴CE=2.
∴CD=CE+DE=2+6=8.
19.(2020春?青羊区期末)如图,△ABC中,AB=AC,∠EAF═∠BAC,BF⊥AE于E交AF于点F,连结CF.
(1)如图1所示,当∠EAF在∠BAC内部时,求证:EF=BE+CF.
(2)如图2所示,当∠EAF的边AE、AF分别在∠BAC外部、内部时,求证:CF=BF+2BE.
【解答】证明:(1)如图,在EF上截取EH=BE,连接AH,
∵EB=EH,AE⊥BF,
∴AB=AH,
∵AB=AH,AE⊥BH,
∴∠BAE=∠EAH,
∵AB=AD,
∴AC=AH,
∵∠EAF═∠BAC
∴∠BAE+∠CAF=∠EAF,
∴∠BAE+∠CAF=∠EAH+∠FAH,
∴∠CAF=∠HAF,
在△ACF和△AHF中,
,
∴△ACF≌△AHF(SAS),
∴CF=HF,
∴EF=EH+HF=BE+CF;
(2)如图,在BE的延长线上截取EN=BE,连接AN,
∵AE⊥BF,BE=EN,AB=AC,
∴AN=AB=AC,
∵AN=AB,AE⊥BN,
∴∠BAE=∠NAE,
∵∠EAF═∠BAC
∴∠EAF+∠NAE=(∠BAC+2∠NAE)
∴∠FAN=∠CAN,
∴∠FAN=∠CAF,
在△ACF和△ANF中,
,
∴△ACF≌△ANF(SAS),
∴CF=NF,
∴CF=BF+2BE.
20.(2020春?文圣区期末)已知:如图,BD、CE是△ABC的高,BD、CE交于点F,BD=CD,CE平分∠ACB.
(1)如图1,试说明BE=CF.
(2)如图2,若点M在边BC上(不与点B重合),MN⊥AB于点N,交BD于点G,∠BMN=∠ACB,请直接写出BN与MG的数量关系,并画出能够说明该结论成立的辅助线,不必书写过程.
【解答】解:(1)∵BD⊥AC,CE⊥AB,
∴∠ADB=∠BDC=∠AEC=90°,
∴∠A+∠ABD=90°,∠A+∠ACE=90°,
∴∠ABD=∠ACE,
在△ABD和△FCD中,
,
∴△ABD≌△FCD(SAS),
∴AB=CF,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
在△ACE和△BCE中,
,
∴△ACE≌△BCE(ASA),
∴AE=BE,
∴BE=AB=CF;
(2)BN=MG,
理由如下:如图,过点M作MH∥AC,交AB于H,交BD于P,
∵BD=CD,BD⊥CD,
∴∠DBC=∠DCB=45°,
∵MH∥AC,
∴∠PMB=∠DCB=∠PBM=45°,∠BPM=∠BDC=90°,
∴BP=PM,
∵∠BHP+∠HBP=90°,∠BHP+∠HMN=90°,
∴∠HBP=∠HMN,
在△BHP和△MGP中,
,
∴△BPH≌△MPG(ASA),
∴GM=BH,
∵∠BMN=∠ACB=22.5°,
∴∠BMN=∠HMN=22.5°,
在△BMN和△HMN中,
,
∴△BMN≌△HMN(ASA)
∴BN=NH,
∴BN=BH=MG.
21.(2020春?沙坪坝区校级月考)如图,CD∥AB,△ABC的中线AE的延长线与CD交于点D.
(1)若AE=3,求DE的长度;
(2)∠DAC的平分线与DC交于点F,连接EF,若AF=DF,AC=DE,求证:AB=AF+EF.
【解答】解:(1)∵CD∥AB,
∴∠B=∠DCE,
∵AE是中线,
∴CE=BE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(ASA),
∴AE=DE=3,
∴DE的长为3;
(2)∵△ABE≌△DCE,
∴AB=CD,
∵AF平分∠DAC,
∴∠CAF=∠DAF,
∵AC=DE,AE=DE,
∴AC=AE,
在△CAF和△EAF中,
,
∴△CAF≌△EAF(SAS),
∴CF=EF,
∴AB=CD=CF+DF=EF+AF.
22.(2020春?南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.
(1)如图1,若∠BED=∠CFD,请说明DE=DF;
(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.
【解答】解:(1)∵DB⊥AM,DC⊥AN,
∴∠DBE=∠DCF=90°,
在△BDE和△CDF中,
∵
∴△BDE≌△CDF(AAS).
∴DE=DF;
(2)EF=FC+BE,
理由:过点D作∠CDG=∠BDE,交AN于点G,
在△BDE和△CDG中,
,
∴△BDE≌△CDG(ASA),
∴DE=DG,BE=CG.
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°.
∴∠FDG=∠CDG+∠CDF=60°,
∴∠EDF=∠GDF.
在△EDF和△GDF中,
,
∴△EDF≌△GDF(SAS).
∴EF=GF,
∴EF=FC+CG=FC+BE.
23.(2020春?龙岗区期末)如图,点O为线段AB上的任意一点(不于A、B重合),分别以AO,BO为一腰在AB的同侧作等腰△AOC和△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD,AD与BC交于点P,AD交CO于点M,BC交DO于点N.
(1)试说明:CB=AD;
(2)若∠COD=70°,求∠APB的度数.
【解答】证明:(1)∵∠AOC=∠BOD,
∴∠AOD=∠BOC,
又∵OA=OC,OB=OD,
∴△AOD≌△COB(SAS),
∴CB=AD;
(2)∵∠COD=70°,
∴∠AOC=∠BOD=55°,
∴∠AOD=∠COD+∠BOD=125°=∠BOC,
∵△AOD≌△COB,
∴∠BCO=∠DAO,
∴∠DAO+∠CBO=∠BCO+∠CBO,
∴180°﹣∠APB=180°﹣∠BOC,
∴∠APB=125°
24.(2020?五华区二模)如图所示,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交BA、BC于点M、N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.请你观察图形,解答下列问题:
(1)求证:△ABC≌△DBC;
(2)若∠A=100°,∠E=50°,求∠ACB的度数.
【解答】解:(1)如图所示,连接MN,NF,
由题可得,BM=BF,MN=FN,BN=BN,
∴△BMN≌△BFN(SSS),
∴∠ABC=∠DBC,
又∵AB=DB,BC=BC,
∴△ABC≌△DBC(SAS);
(2)∵∠A=100°,∠E=50°,
∴∠ABE=30°,
∴∠ABC=∠ABD=15°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣100°﹣15°=65°.
25.(2020?扬中市模拟)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
【解答】证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
,
∴△ABE≌△ACD(ASA),
∴AE=AD;
(2)解:∵∠ACB=65°,AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,
∵∠ABD=∠ACD,∠AOB=∠COD,
∴∠BDC=∠BAC=50°.
三.填空题(共9小题)
26.(2020春?碑林区校级期末)如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为 4 m.
【解答】解:∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE,
在△ABC和△DEF中,,
∴△ABC≌△DEF(AAS),
∴BC=EF,
∴BC﹣FC=EF﹣FC,
即BF=CE=5m,
∴FC=BE﹣BF﹣CE=14m﹣5m﹣5m=4m;
故答案为:4.
27.(2020春?三明期末)如图,要测量池塘两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD.再作出BF的垂线DE,使A、C、E三点在一条直线上,通过证明△ABC≌△DEC,得到DE的长就等于AB的长,这里证明三角形全等的依据是 ASA .
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故答案为:ASA.
28.(2020春?彭州市期末)两个全等的直角三角尺如图所示放置在∠AOB的两边上,其中直角三角尺的短直角边分别与∠AOB的两边上,两个直角三角尺的长直角边交于点P,连接OP,且OM=ON,若∠AOB=60°,OM=6cm,则线段OP= 4 cm.
【解答】解:在Rt△OMP和Rt△ONP中,OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∵∠AOB=60°,
∴∠MOP=∠NOP=30°,
∵∠OMP=90°,
∴OP=2MP,OM=MP=6cm,
∴MP=2cm,
∴OP=4cm,
故答案为:4.
29.(2019秋?松滋市期末)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 20 cm.
【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
30.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 ③⑤⑥ .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
【解答】解:延长EB到G,使BG=DF,连接AG,
∵AB⊥CB,AD⊥CD,
∴∠D=∠ABG=90°,
在△ADF和△ABG中
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠G=∠DFA,∠DAF=∠BAG,
∵∠EAF=70°,∠DAB=140°,
∴∠DAF+∠EAB=∠DAB﹣∠FAE=140°﹣70°=70°,
∴∠EAG=∠EAB+∠BAG=∠EAB+∠FAD=70°,
∴∠FAE=∠EAG=70°,
在△FAE和△GAE中
,
∴△FAE≌△GAE(SAS),
∴∠FEA=∠GEA,∠G=∠EFA,EF=EG,
∴EF=EB+DF,∠FAE≠∠EAB,故⑤正确,④错误;
∴∠G=∠EFA=∠DFA,即AF平分∠DFE,故③正确;
∵CF+CE>EF,EF=DF+BE,
∴CF+CE>DF+BE,故⑥正确;
根据已知不能推出△ADF≌△ABE,故①错误,②错误;
故答案为:③⑤⑥.
31.(2020春?市中区校级期末)如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=50°,则∠DFE= 40° .
【解答】解:连接BD、AE,
∵DA⊥AB,FC⊥AB,
∴∠DAB=∠BCF=90°,
在△DAB和△BCF中,
,
∴△DAB≌△BCF(SAS),
∴BD=BF,∠ADB=∠ABF,
∴∠BDF=∠BFD,
∵∠DAB=90°,
∴∠ADB+∠DBA=90°,
∴∠DBF=∠ABD+∠ABF=90°,
∴∠BFD=∠BDF=45°,
同理∠AFE=45°,
∴∠DFE=45°+45°﹣50°=40°,
故答案为:40°.
32.(2020春?迁西县期末)如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为4和9,则n的面积为 13 .
【解答】解:由于m、q、n都是正方形,所以AC=CD,∠ACD=90°;
∵∠ACB+∠DCE=∠ACB+∠BAC=90°,
∴∠BAC=∠DCE,且AC=CD,∠ABC=∠DEC=90°
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sn=Sm+Sq=4+9=13,
∴正方形n的面积为13,
故答案为:13.
33.(2020春?福田区期中)如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有 ①②③④ .(填上所有正确结论的序号)
【解答】解:连接BO,如图1所示:
∵AB=AC,AD⊥BC,
∴BO=CO,
∴∠OBC=∠OCB,
又∵OP=OC,
∴OP=OB,
∴∠OBP=∠OPB,
又∵在等腰△ABC中∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠OBC+∠OBP=∠OCB+∠ACO,
∴∠OBP=∠ACO,
∴∠APO=∠ACO,故①正确;
又∵∠ABC=∠PBO+∠CBO=30°,
∴∠APO+∠DCO=30°,
∵∠PBC+∠BPC+∠BCP=180°,∠PBC=30°,
∴∠BPC+∠BCP=150°,
又∵∠BPC=∠APO+∠CPO,
∠BCP=∠BCO+∠PCO,
∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
又∵∠POC+∠OPC+∠OCP=180°,
∴∠POC=60°,
又∵OP=OC,
∴△OPC是等边三角形,
∴PC=PO,∠PCO=60°,故③正确;
∴∠APO+∠DCO+∠PCO=30°+60°,
即:∠APO+∠PCB=90°,故②正确;
在线段AC上截取AE=AP,连接PE,如图2所示:
∵∠BAC+∠CAP=180°,∠BAC=120°,
∴∠CAP=60°,
∴△APE是等边三角形,
∴AP=EP,
又∵△OPC是等边三角形,
∴OP=CP,
又∵∠APE=∠APO+∠OPE=60°,
∠CPO=∠CPE+∠OPE=60°,
∴∠APO=∠EPC,
在△APO和△EPC中,,
∴△APO≌△EPC(SAS),
∴AO=EC,
又∵AC=AE+EC,AE=AP,
∴AO+AP=AC,故④正确;
故答案为:①②③④.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
