第1章 三角形的初步知识培优习题精选(含解析)
文档属性
| 名称 | 第1章 三角形的初步知识培优习题精选(含解析) |  | |
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 08:21:36 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
八下第一章三角形的初步知识培优习题精选
一.选择题(共19小题)
1.(2020春?雨花区期末)如图,已知CD和BE是△ABC的角平分线,∠A=60°,则∠BOC=( )
A.60° B.100° C.120° D.150°
2.(2020?雁塔区校级模拟)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F,交边BC于点E,连接DE.若∠ABC=40°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
3.(2020春?义乌市期末)如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G∥BC,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
4.(2020春?岱岳区期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠BAE=30°,∠CAD=20°,则∠B=( )
A.45° B.60° C.50° D.55°
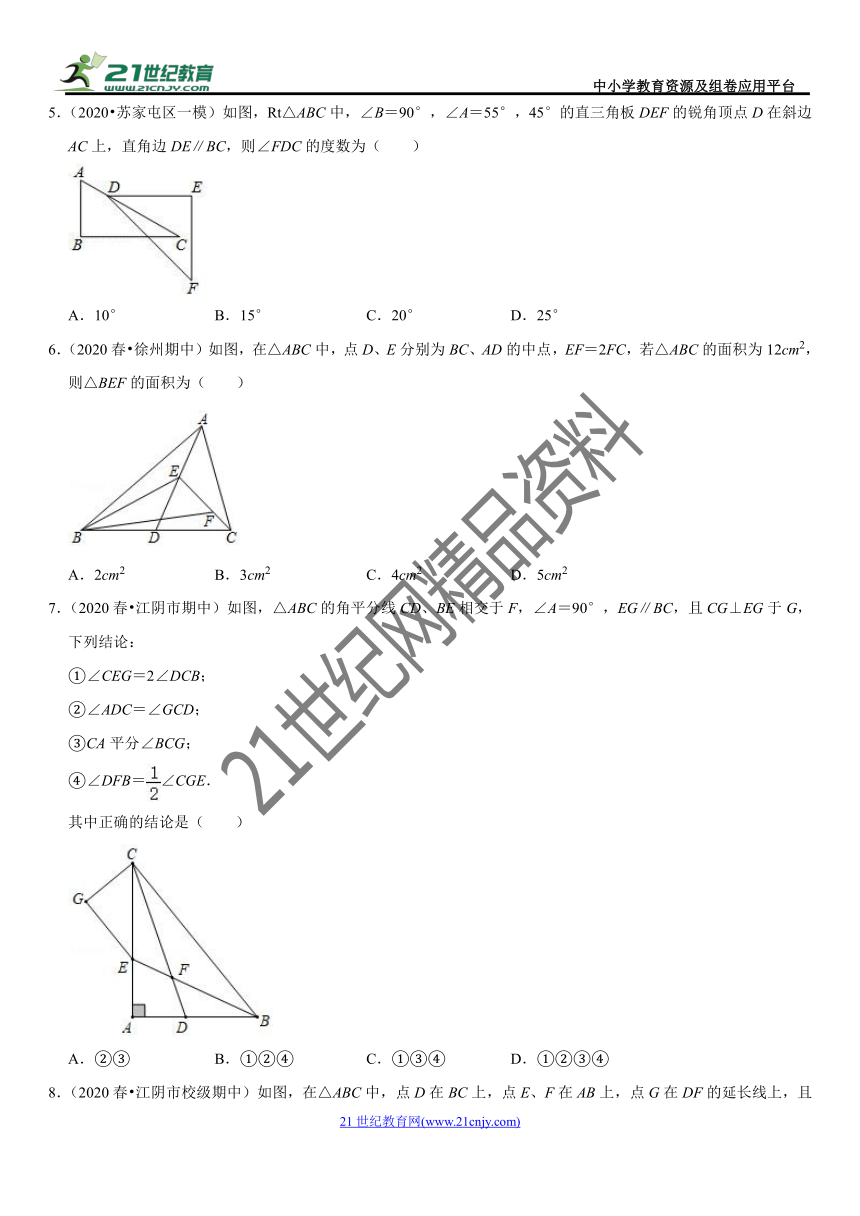
5.(2020?苏家屯区一模)如图,Rt△ABC中,∠B=90°,∠A=55°,45°的直三角板DEF的锐角顶点D在斜边AC上,直角边DE∥BC,则∠FDC的度数为( )
A.10° B.15° C.20° D.25°
6.(2020春?徐州期中)如图,在△ABC中,点D、E分别为BC、AD的中点,EF=2FC,若△ABC的面积为12cm2,则△BEF的面积为( )
A.2cm2 B.3cm2 C.4cm2 D.5cm2
7.(2020春?江阴市期中)如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;
②∠ADC=∠GCD;
③CA平分∠BCG;
④∠DFB=∠CGE.
其中正确的结论是( )
A.②③ B.①②④ C.①③④ D.①②③④
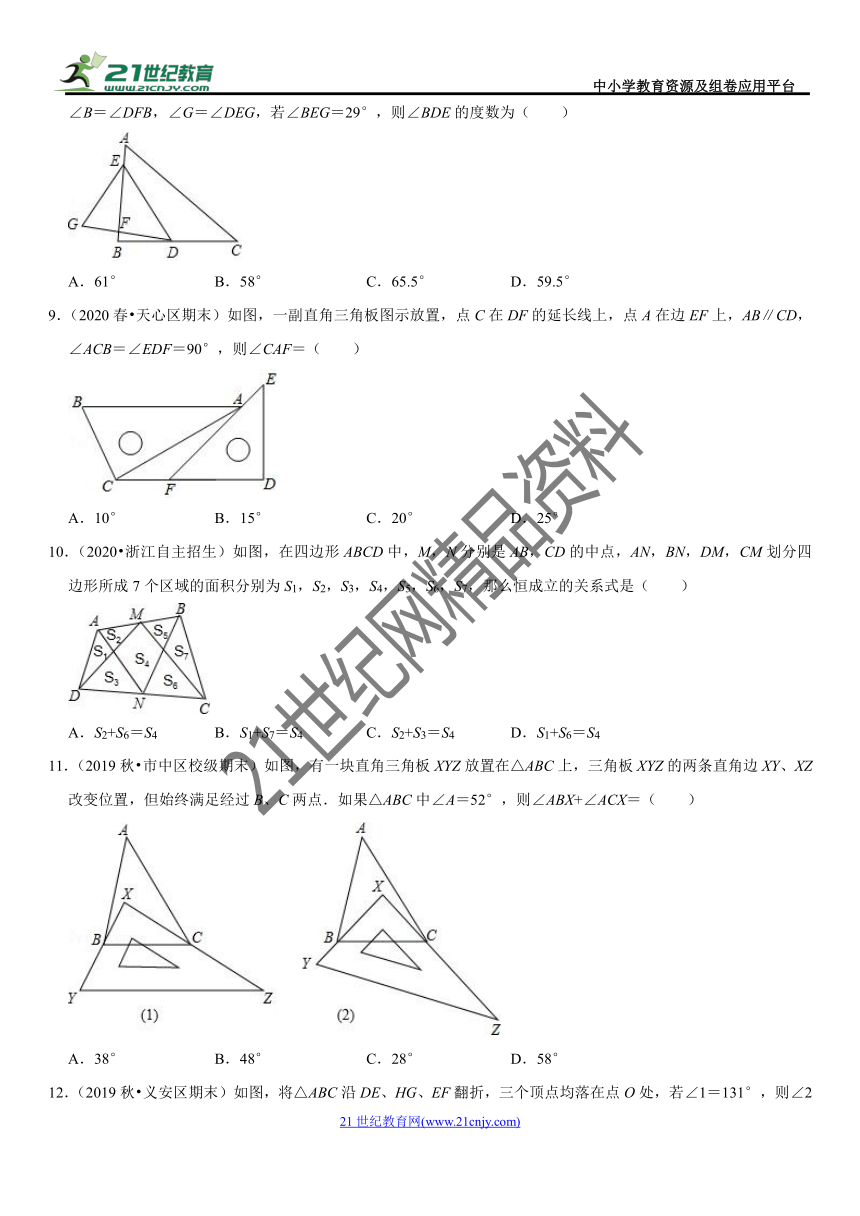
8.(2020春?江阴市校级期中)如图,在△ABC中,点D在BC上,点E、F在AB上,点G在DF的延长线上,且∠B=∠DFB,∠G=∠DEG,若∠BEG=29°,则∠BDE的度数为( )
A.61° B.58° C.65.5° D.59.5°
9.(2020春?天心区期末)如图,一副直角三角板图示放置,点C在DF的延长线上,点A在边EF上,AB∥CD,∠ACB=∠EDF=90°,则∠CAF=( )
A.10° B.15° C.20° D.25°
10.(2020?浙江自主招生)如图,在四边形ABCD中,M,N分别是AB,CD的中点,AN,BN,DM,CM划分四边形所成7个区域的面积分别为S1,S2,S3,S4,S5,S6,S7,那么恒成立的关系式是( )
A.S2+S6=S4 B.S1+S7=S4 C.S2+S3=S4 D.S1+S6=S4
11.(2019秋?市中区校级期末)如图,有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ改变位置,但始终满足经过B、C两点.如果△ABC中∠A=52°,则∠ABX+∠ACX=( )
A.38° B.48° C.28° D.58°
12.(2019秋?义安区期末)如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
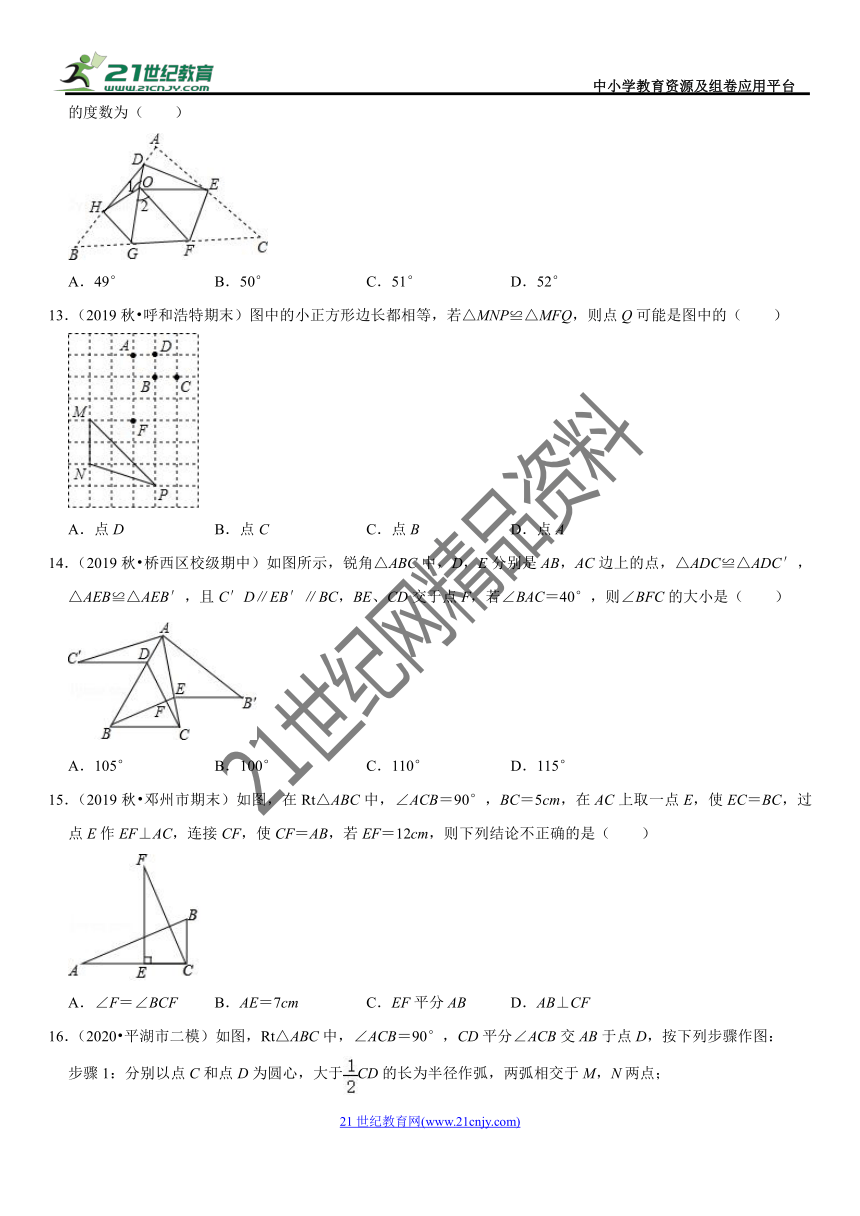
13.(2019秋?呼和浩特期末)图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
14.(2019秋?桥西区校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105° B.100° C.110° D.115°
15.(2019秋?邓州市期末)如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF B.AE=7cm C.EF平分AB D.AB⊥CF
16.(2020?平湖市二模)如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
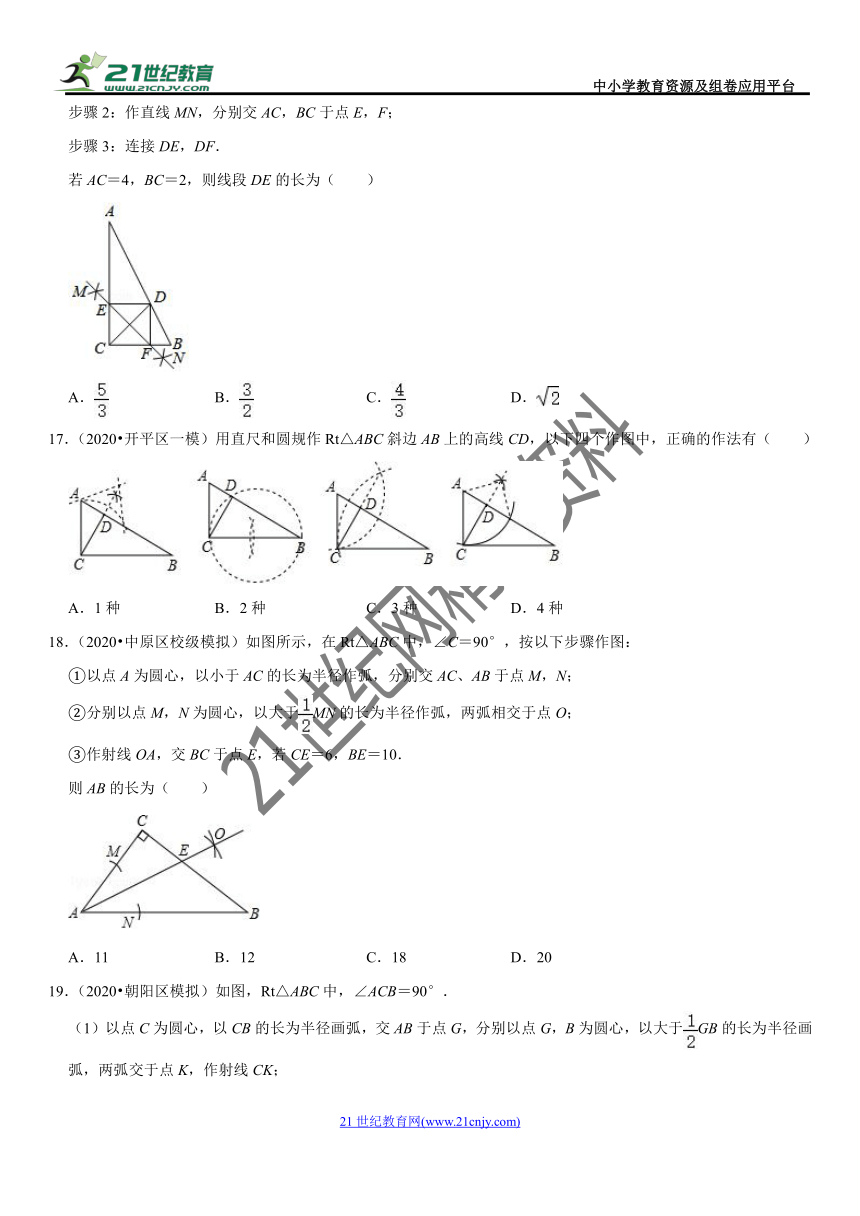
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为( )
A. B. C. D.
17.(2020?开平区一模)用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,正确的作法有( )
A.1种 B.2种 C.3种 D.4种
18.(2020?中原区校级模拟)如图所示,在Rt△ABC中,∠C=90°,按以下步骤作图:
①以点A为圆心,以小于AC的长为半径作弧,分别交AC、AB于点M,N;
②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点O;
③作射线OA,交BC于点E,若CE=6,BE=10.
则AB的长为( )
A.11 B.12 C.18 D.20
19.(2020?朝阳区模拟)如图,Rt△ABC中,∠ACB=90°.
(1)以点C为圆心,以CB的长为半径画弧,交AB于点G,分别以点G,B为圆心,以大于GB的长为半径画弧,两弧交于点K,作射线CK;
(2)以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于点N,分别以点M,N为圆心,以大于MN的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E;
(3)过点D作DF⊥AB交AB的延长线于点F,连接CF.
根据以上操作过程及所作图形,有如下结论:
①CE=CD;
②BC=BE=BF;
③S四边形CDFB=CF?BD;
④∠BCF=∠BCE.
所有正确结论的序号为( )
A.①②③ B.①③ C.②④ D.③④
二.填空题(共10小题)
20.(2019秋?包河区期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为 .
21.(2019秋?滑县期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是 .
22.(2019秋?镇原县期末)如图,已知△ABC≌△A′BC′,AA′∥BC,∠ABC=70°,则∠CBC′= .
23.(2019春?滨湖区期中)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为
24.(2019秋?海州区期中)如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB= °.
25.(2018秋?阜南县期末)在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为 .
26.(2019秋?江都区期末)如图,在△PAB中,PA=PB,D、E、F分别是边PA,PB,AB上的点,且AD=BF,BE=AF,若∠DFE=40°,则∠P= °.
27.(2020春?武侯区期末)如图,在Rt△ACB中,∠C=90°,AB=2,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则△ABD的面积为 .
28.(2019秋?和平区期末)定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)图①是顶角为36°的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为36°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)图③是顶角为45°的等腰三角形,请你在图③中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数 .
(3)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,则x所有可能的值为 .
29.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
三.解答题(共10小题)
30.(2020春?浦东新区期末)已知线段a、b,作出条一线段,使它等于2a﹣b.(用直尺和圆规作图,不写作法,保留作图痕迹).
31.(2020春?南岸区期末)如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠B=70°,求∠C的度数;
(2)若AE=AC,AD平分∠BDE是否成立?请说明理由.
32.(2020春?南岗区校级期中)如图,在△ABC中,BD,CE分别是AC,AB边上的高,在BD上截取BF=AC,延长CE至点G使CG=AB,连接AF,AG.
(1)如图1,求证:AG=AF;
(2)如图2,若BD恰好平分∠ABC,过点G作GH⊥AC交CA的延长线于点H,请直接写出图中所有的全等三角形并用全等符号连接.
33.(2019秋?鲤城区校级期末)已知,在△ABC中,AC=BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM,BN于点D,E.
(1)如图1.若CD=CE.求∠ABE的大小;
(2)如图2.∠ABC=∠DEB=60°.求证:AD+DC=BE.
34.(2018秋?寿县期末)如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
35.(2020春?裕华区校级期末)(1)已知△ABC中,∠B>∠C,AD⊥BC于D,AE平分∠BAC,∠B=70°,∠C=40°,求∠DAE的度数.
(2)在图2中,∠B=x,∠C=y,其他条件不变,若把“AD⊥BC于D改为“F是AE上一点,FD⊥BC于D“,试用x、y表示∠DFE= :
(3)在图3中,若把(2)中的“点F在AE上“改为点F是AE延长线上一点”,其余条件不变,试用x、y表示∠DFE= ;
(4)在图3中,分别作出∠BAE和∠EDF的角平分线,交于点P,如图4.试用x、y表示∠P= .
36.(2020春?雨花区校级期末)如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,CD⊥AB,垂足为D,延长CE与外角∠ABG的平分线交于点F.
(1)若∠A=60°,求∠DCE和∠F的度数;
(2)若∠A=n°(0<n<90),请直接写出∠DCE和∠F的度数(用含n的代数式表示);
(3)若△FCB高FH和∠DCB的角平分线交于点Q,在(2)的条件下求∠CQH的度数(用含n的代数式表示).
37.(2020春?新都区期末)如图1,∠MON=80°,点A、B在∠MON的两条边上运动,∠OAB与∠OBA的平分线交于点C.
(1)点A、B在运动过程中,∠ACB的大小会变吗?如果不会,求出∠ACB的度数;如果会,请说明理由.
(2)如图2,AD是∠MAB的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,∠E的大小会变吗?如果不会,求出∠E的度数;如果会,请说明理由.
(3)在(2)的条件下,若∠MON=n,请直接写出∠ACB= ;∠E= .
38.(2020春?清江浦区期末)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC度数.
思路点拨:
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可分别求出∠APE、∠CPE的度数,从而可求出∠APC的度数;
小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∠APC的度数;
小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∠APC的度数.
问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∠APC的度数为 °;
问题迁移:(1)如图5,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
八下第一章三角形的初步知识培优习题精选
参考答案与试题解析
一.选择题(共19小题)
1.(2020春?雨花区期末)如图,已知CD和BE是△ABC的角平分线,∠A=60°,则∠BOC=( )
A.60° B.100° C.120° D.150°
【解答】解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵CD和BE是△ABC的角平分线,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)=60°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=120°,
故选:C.
2.(2020?雁塔区校级模拟)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F,交边BC于点E,连接DE.若∠ABC=40°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
【解答】解:∵∠B=40°,∠C=50°,
∴∠BAC=90°,
∵∠ABF=∠EBF,BF=BF,∠BFA=∠BFE=90°,
∴△BFA≌△BFE(ASA),
∴BA=BE,
∵BD=BD,
∴△BDA≌△BDE(SAS),
∴∠BED=∠BAD=90°,
∴∠CED=90°,
∴∠CDE=90°﹣50°=40°,
故选:B.
3.(2020春?义乌市期末)如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G∥BC,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
【解答】解:设∠ADB′=γ,∠AGC′=β,∠CEB′=y,∠C′FE=x,
∵B'D∥C'G,
∴γ+β=∠B+∠C=α,
∵EB′∥FG,
∴∠CFG=∠CEB′=y,
∴x+2y=180° ①,
∵γ+y=2∠B,β+x=2∠C,
∴γ+y+β+x=2α,
∴x+y=α②,
②×2﹣①可得x=2α﹣180°,
∴∠C′FE=2α﹣180°.
故选:D.
4.(2020春?岱岳区期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠BAE=30°,∠CAD=20°,则∠B=( )
A.45° B.60° C.50° D.55°
【解答】解:∵AE平分∠BAC,
∴∠BAE=∠CAE=30°,
∴∠EAD=∠EAC﹣∠DAC=30°﹣20°=10°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠AED=90°﹣∠EAD=80°,
∵∠AED=∠B+∠BAE,
∴∠B=80°﹣30°=50°,
故选:C.
5.(2020?苏家屯区一模)如图,Rt△ABC中,∠B=90°,∠A=55°,45°的直三角板DEF的锐角顶点D在斜边AC上,直角边DE∥BC,则∠FDC的度数为( )
A.10° B.15° C.20° D.25°
【解答】解:∵∠B=90°,∠A=55°,
∴∠C=35°,
∵DE∥BC,
∴∠C=∠EDC=35°,
∵∠EDF=45°,
∴∠CDF=∠EDF﹣∠EDC=45°﹣35°=10°,
故选:A.
6.(2020春?徐州期中)如图,在△ABC中,点D、E分别为BC、AD的中点,EF=2FC,若△ABC的面积为12cm2,则△BEF的面积为( )
A.2cm2 B.3cm2 C.4cm2 D.5cm2
【解答】解:∵D是BC的中点,
∴S△ABD=S△ADC(等底等高的三角形面积相等),
∵E是AD的中点,
∴S△ABE=S△BDE,S△ACE=S△CDE(等底等高的三角形面积相等),
∴S△ABE=S△DBE=S△DCE=S△AEC,
∴S△BEC=S△ABC=6cm2.
∵EF=2FC,
∴S△BEF=S△BCE,
∴S△BEF=S△BEC=4cm2.
故选:C.
7.(2020春?江阴市期中)如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;
②∠ADC=∠GCD;
③CA平分∠BCG;
④∠DFB=∠CGE.
其中正确的结论是( )
A.②③ B.①②④ C.①③④ D.①②③④
【解答】解:∵EG∥BC,
∴∠CEG=∠BCA,
∵CD平分∠ACB,
∴∠BCA=2∠DCB,
∴∠CEG=2∠DCB,故①正确,
∵CG⊥EG,
∴∠G=90°,
∴∠GCE+∠CEG=90°,
∵∠A=90°,
∴∠BCA+∠ABC=90°,
∵∠CEG=∠ACB,
∴∠ECG=∠ABC,
∵∠ADC=∠ABC+∠DCB,∠GCD=∠ECG+∠ACD,∠ACD=∠DCB,
∴∠ADC=∠GCD,故②正确,
假设AC平分∠BCG,则∠ECG=∠ECB=∠CEG,
∴∠ECG=∠CEG=45°,显然不符合题意,故③错误,
∵∠DFB=∠FCB+∠FBC=(∠ACB+∠ABC)=45°,∠CGE=45°,
∴∠DFB=∠CGE,故④正确,
故选:B.
8.(2020春?江阴市校级期中)如图,在△ABC中,点D在BC上,点E、F在AB上,点G在DF的延长线上,且∠B=∠DFB,∠G=∠DEG,若∠BEG=29°,则∠BDE的度数为( )
A.61° B.58° C.65.5° D.59.5°
【解答】解:设∠DEF=x,∠EDF=y,则∠DFB=∠B=x+y,∠BDF=180°﹣2x﹣2y,∠G=∠DEG=x+29°,
∵∠G+∠FEG=∠B+∠BDF,
∴x+29°+29°=x+y+180°﹣2x﹣2y,
∴2x+y=122°,
∴∠BDE=∠BDF+∠EDF=180°﹣2x﹣2y+y=180°﹣2x﹣y=58°,
故选:B.
9.(2020春?天心区期末)如图,一副直角三角板图示放置,点C在DF的延长线上,点A在边EF上,AB∥CD,∠ACB=∠EDF=90°,则∠CAF=( )
A.10° B.15° C.20° D.25°
【解答】解:∵AB∥CD,
∴∠BAC=∠ACD=30°,
∵∠AFD=∠CAF+∠ACF=45°,
∴∠CAF=45°﹣30°=15°,
故选:B.
10.(2020?浙江自主招生)如图,在四边形ABCD中,M,N分别是AB,CD的中点,AN,BN,DM,CM划分四边形所成7个区域的面积分别为S1,S2,S3,S4,S5,S6,S7,那么恒成立的关系式是( )
A.S2+S6=S4 B.S1+S7=S4 C.S2+S3=S4 D.S1+S6=S4
【解答】解:过A作AE⊥DC于E,过M作MH⊥DC于H,过B作BQ⊥DC于Q,
则AE∥MH∥BQ,
∵M为AB中点,
∴H为EQ中点,
即MH是梯形AEQB的中位线,
∴2MH=AE+BQ,
∵S3+S4+S6=S△MDC=×DC×MH,
S7+S6=S△BNC=×NC×BQ,
S1+S3=S△ADN=×DN×AE,
∵N为DC中点,
∴DN=CN,
∴S7+S6+S1+S3,
=×NC×BQ+×DN×AE,
=DN×(AE+BQ),
=DN×2MH,
=DN×MH,
=CD×MH,
∴S7+S6+S1+S3=S3+S4+S6,
∴S4=S1+S7;
故选:B.
11.(2019秋?市中区校级期末)如图,有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ改变位置,但始终满足经过B、C两点.如果△ABC中∠A=52°,则∠ABX+∠ACX=( )
A.38° B.48° C.28° D.58°
【解答】解:连接AX,
∵∠BXC=90°,
∴∠AXB+∠AXC=360°﹣∠BXC=270°,
∵∠A=52°,
∴∠BAX+∠CAX=52°,
∵∠ABX+∠BAX+∠AXB=180°,∠ACX+∠CAX+∠AXC=180°,
∴∠ABX+∠ACX=360°﹣270°﹣52°=38°,
故选:A.
12.(2019秋?义安区期末)如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
【解答】解:由折叠得:∠HOG=∠B,∠DOE=∠A,∠EOF=∠C,
∵∠A+∠B+∠C=180°,
∴∠HOG+∠DOE+∠EOF=180°,
∵∠1+∠2+∠HOG+∠DOE+∠EOF=360°,
∴∠1+∠2=180°,
∵∠1=131°,
∴∠2=180°﹣131°=49°,
故选:A.
13.(2019秋?呼和浩特期末)图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
【解答】解:观察图象可知△MNP≌△MFD.
故选:A.
14.(2019秋?桥西区校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105° B.100° C.110° D.115°
【解答】解:延长C′D交AB′于H.
∵△AEB≌△AEB′,
∴∠ABE=∠AB′E,
∵C′H∥EB′,
∴∠AHC′=∠AB′E,
∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,
∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:B.
15.(2019秋?邓州市期末)如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF B.AE=7cm C.EF平分AB D.AB⊥CF
【解答】解:∵EF⊥AC,∠ACB=90°,
∴∠FEC=∠ACB=90°,
∴∠F+∠FCE=∠FCE+∠BCF=90°,
∴∠F=∠BCF;故A选项正确;
在Rt△ACB与Rt△FEC中,,
∴Rt△ACB≌Rt△FEC(HL),
∴AC=EF=12,CE=BC=5cm,
∴AE=AC﹣CE=7cm,故B选项正确;
∵Rt△ACB≌Rt△FEC,
∴∠A=∠F,
∵∠ADE=∠EDF,
∴∠FED=∠AEF=90°,
∴AB⊥CF,故D选项正确;
∵∠AED=∠ACB,
∴DE∥BC,
∴==,
∴AD≠DB,
∴EF不平分AB,故C选项错误,
故选:C.
16.(2020?平湖市二模)如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为( )
A. B. C. D.
【解答】解:由作图可知,四边形ECFD是正方形,
∴DE=DF=CE=CF,∠DEC=∠DFC=90°,
∵S△ACB=S△ADC+S△CDB,
∴×AC×BC=×AC×DE+×BC×DF,
∴DE==,
故选:C.
17.(2020?开平区一模)用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,正确的作法有( )
A.1种 B.2种 C.3种 D.4种
【解答】解:(1)根据垂径定理作图的方法可知:
CD是Rt△ABC斜边AB上的高线,故作法正确;
(2)根据直径所对圆周角是直角的方法可知:
CD是Rt△ABC斜边AB上的高线,故作法正确;
(3)根据相交两圆的公共弦的性质可知:
CD是Rt△ABC斜边AB上的高线,故作法正确;
(4)无法证明CD是Rt△ABC斜边AB上的高线,故作法不正确;
综上所述:正确的作法有3种.
故选:C.
18.(2020?中原区校级模拟)如图所示,在Rt△ABC中,∠C=90°,按以下步骤作图:
①以点A为圆心,以小于AC的长为半径作弧,分别交AC、AB于点M,N;
②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点O;
③作射线OA,交BC于点E,若CE=6,BE=10.
则AB的长为( )
A.11 B.12 C.18 D.20
【解答】解:过点E作DE⊥AB于点D,
由作图知AP平分∠BAC,
∵∠C=∠ADE=90°,
∴CE=DE=6,
∵BE=10,
∴BD=8,
∵AD=AD,CE=DE,
∴Rt△ACE≌Rt△ADE(HL),
∴AC=AD,
设AC=AD=x,
由AC2+BC2=AB2得x2+162=(x+8)2,
解得:x=6,即AC=12,
∵AB=20,
故选:D.
19.(2020?朝阳区模拟)如图,Rt△ABC中,∠ACB=90°.
(1)以点C为圆心,以CB的长为半径画弧,交AB于点G,分别以点G,B为圆心,以大于GB的长为半径画弧,两弧交于点K,作射线CK;
(2)以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于点N,分别以点M,N为圆心,以大于MN的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E;
(3)过点D作DF⊥AB交AB的延长线于点F,连接CF.
根据以上操作过程及所作图形,有如下结论:
①CE=CD;
②BC=BE=BF;
③S四边形CDFB=CF?BD;
④∠BCF=∠BCE.
所有正确结论的序号为( )
A.①②③ B.①③ C.②④ D.③④
【解答】解:如图,连接CF,交BD于点H,
由作图过程可知:
CE是BG的垂直平分线,BD是∠CBF的平分线,
设CE与AB交于点Q,
∴∠CQA=∠DFA=90°,
∴CQ∥DF,
∴∠CED=∠FDE,
∵BD是∠CBF的平分线,
∴∠CBD=∠FBD,
∵∠BCD=∠BFD=90°,
BD=BD,
∴△BCD≌△BFD(AAS),
∴∠CDB=∠FDB,
∴∠CDB=∠CED,
∴CE=CD,
所以①正确;
∵△BCD≌△BFD(AAS),
∴BC=BF,
但是BC≠BE,
∴②不正确;
∵S四边形CDFB=S△BCD+S△BFD
=BD?CH+BD?FH
=CF?BD.
∴③正确;
∵△BCE与△BCF不全等,
∴∠BCE≠∠BCF,
∴④不正确.
所以正确结论的序号为①③.
故选:B.
二.填空题(共10小题)
20.(2019秋?包河区期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为 70° .
【解答】解:∵△ABC≌△ADE,
∴AB=AD,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵∠EAC=40°,
∴∠BAD=40°,
∵AB=AD,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
故答案为:70°.
21.(2019秋?滑县期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是 180° .
【解答】解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个全等三角形,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
故答案为:180°
22.(2019秋?镇原县期末)如图,已知△ABC≌△A′BC′,AA′∥BC,∠ABC=70°,则∠CBC′= 40° .
【解答】解:∵AA′∥BC,
∴∠A′AB=∠ABC=70°,
∵△ABC≌△A′BC′,
∴BA=BA′,∠A′BC=∠ABC=70°,
∴∠A′AB=∠AA′B=70°,
∴∠A′BA=40°,
∴∠ABC′=30°,
∴∠CBC′=40°,
故答案为:40°.
23.(2019春?滨湖区期中)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为 48
【解答】解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48.
故答案为48.
24.(2019秋?海州区期中)如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB= 60 °.
【解答】解:∵△ABC≌△ADE,∠B=50°,
∴∠D=∠B=50°,∠EAD=∠CAB,
∵∠AED=105°,
∴∠EAD=180°﹣∠D﹣∠AED=25°,
∴∠CAB=25°,
∵∠CAD=10°,
∴∠EAB=∠EAD+∠DAC+∠CAB=25°+10°+25°=60°
25.(2018秋?阜南县期末)在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为 135° .
【解答】解:∵在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴∠4=∠2,
∵∠1+∠4=90°,
∴∠1+∠2=90°,
∵AE=DE,∠AED=90°,
∴∠3=45°,
∴∠1+∠2+∠3=135°,
故答案为:135°
26.(2019秋?江都区期末)如图,在△PAB中,PA=PB,D、E、F分别是边PA,PB,AB上的点,且AD=BF,BE=AF,若∠DFE=40°,则∠P= 100 °.
【解答】解:∵PA=PB,
∴∠A=∠B,
在△ADF和△BFE中,
,
∴△ADF≌△BFE(SAS),
∴∠ADF=∠BFE,
∵∠DFB=∠DFE+∠EFB=∠A+∠ADF,
∴∠A=∠DFE=40°,
∴∠P=180°﹣∠A﹣∠B=100°,
故答案为:100.
27.(2020春?武侯区期末)如图,在Rt△ACB中,∠C=90°,AB=2,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则△ABD的面积为 .
【解答】解:如图,过点D作DH⊥AB于H.
∵DC⊥BC,DH⊥AB,BD平分∠ABC,
∴DH=CD=1,
∴S△ABD=?AB?DH=×2×1=,
故答案为.
28.(2019秋?和平区期末)定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)图①是顶角为36°的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为36°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)图③是顶角为45°的等腰三角形,请你在图③中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数 90°、135°、45° .
(3)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,则x所有可能的值为 20°或40° .
【解答】解:
(1)在图②中用不同于图①的方法画出顶角为36°的等腰三角形的三分线;
(2)在图③中画出顶角为45°的等腰三角形的三分线.
每个等腰三角形顶角的度数为:90°、135°、45°.
故答案为:90°、135°、45°.
(3)如下图作△ABC,
①如图1:当AD=AE时,
∵2x+x=30+30,
∴x=20.
②如图2:当AD=DE时,
∵2x+x+30+30=180.
∴x=40.
所以x的所有可能的值为20°或40°.
故答案为20°或40°.
29.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 ③⑤⑥ .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
【解答】解:延长EB到G,使BG=DF,连接AG,
∵AB⊥CB,AD⊥CD,
∴∠D=∠ABG=90°,
在△ADF和△ABG中
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠G=∠DFA,∠DAF=∠BAG,
∵∠EAF=70°,∠DAB=140°,
∴∠DAF+∠EAB=∠DAB﹣∠FAE=140°﹣70°=70°,
∴∠EAG=∠EAB+∠BAG=∠EAB+∠FAD=70°,
∴∠FAE=∠EAG=70°,
在△FAE和△GAE中
,
∴△FAE≌△GAE(SAS),
∴∠FEA=∠GEA,∠G=∠EFA,EF=EG,
∴EF=EB+DF,∠FAE≠∠EAB,故⑤正确,④错误;
∴∠G=∠EFA=∠DFA,即AF平分∠DFE,故③正确;
∵CF+CE>EF,EF=DF+BE,
∴CF+CE>DF+BE,故⑥正确;
根据已知不能推出△ADF≌△ABE,故①错误,②错误;
故答案为:③⑤⑥.
三.解答题(共10小题)
30.(2020春?浦东新区期末)已知线段a、b,作出条一线段,使它等于2a﹣b.(用直尺和圆规作图,不写作法,保留作图痕迹).
【解答】解:如图,线段OF即为所求.
31.(2020春?南岸区期末)如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠B=70°,求∠C的度数;
(2)若AE=AC,AD平分∠BDE是否成立?请说明理由.
【解答】解:(1)∵∠B=70°,AB=AD,
∴∠ADB=∠B=70°,
∵∠B+∠BAD+∠ADB=180°,
∴∠BAD=40°,
∵∠CAE=∠BAD,
∴∠CAE=40°,
∵AE∥BC,
∴∠C=∠CAE=40°;
(2)AD平分∠BDE,
理由是:∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS)
∴∠B=∠ADE,
∵∠B=∠ADB,
∴∠ADE=∠ADB,
即AD平分∠BDE.
32.(2020春?南岗区校级期中)如图,在△ABC中,BD,CE分别是AC,AB边上的高,在BD上截取BF=AC,延长CE至点G使CG=AB,连接AF,AG.
(1)如图1,求证:AG=AF;
(2)如图2,若BD恰好平分∠ABC,过点G作GH⊥AC交CA的延长线于点H,请直接写出图中所有的全等三角形并用全等符号连接.
【解答】证明:(1)∵BD、CE分别是AC、AB两条边上的高,
∴∠AEC=∠ADB=90°,
∴∠ABD+∠BAD=∠ACE+∠CAE=90°,
∴∠ABD=∠ACG,
在△AGC与△FAB中,,
∴△AGC≌△FAB(SAS),
∴AG=AF;
(2)图中全等三角形有△AGC≌△FAB,由得出△CGH≌△BAD,
由得出Rt△AGH≌Rt△AFD,△ABD≌△CBD;△CBD≌△GCH.
33.(2019秋?鲤城区校级期末)已知,在△ABC中,AC=BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM,BN于点D,E.
(1)如图1.若CD=CE.求∠ABE的大小;
(2)如图2.∠ABC=∠DEB=60°.求证:AD+DC=BE.
【解答】(1)解:如图1,延长AC交BN于点F,
∵AM∥BN,
∴∠DAF=∠AFB,
在△ADC和△FEC中,,
∴△ADC≌△FEC(AAS),
∴AC=FC,
∵AC=BC,
∴BC=AC=FC=AF,
∴△ABF是直角三角形,
∴∠ABE=90°;
(2)证明:如图2,在EB上截取EH=EC,连CH,
∵AC=BC,∠ABC=60°,
∴△ABC为等边三角形,
∵∠DEB=60°,
∴△CHE是等边三角形,
∴∠CHE=60°,∠HCE=60°,
∴∠BHC=120°,
∵AM∥BN,
∴∠ADC+∠BEC=180°,
∴∠ADC=120°,
∴∠DAC+∠DCA=60°,
又∵∠DCA+∠ACB+∠BCH+∠HCE=180°,
∴∠DCA+∠BCH=60°,
∴∠DAC=∠BCH,
在△DAC与△HCB中,,
∴△DAC≌△HCB(AAS),
∴AD=CH,DC=BH,
又∵CH=CE=HE,
∴BE=BH+HE=DC+AD,
即AD+DC=BE.
34.(2018秋?寿县期末)如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
【解答】解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
35.(2020春?裕华区校级期末)(1)已知△ABC中,∠B>∠C,AD⊥BC于D,AE平分∠BAC,∠B=70°,∠C=40°,求∠DAE的度数.
(2)在图2中,∠B=x,∠C=y,其他条件不变,若把“AD⊥BC于D改为“F是AE上一点,FD⊥BC于D“,试用x、y表示∠DFE= (x﹣y) :
(3)在图3中,若把(2)中的“点F在AE上“改为点F是AE延长线上一点”,其余条件不变,试用x、y表示∠DFE= (x﹣y) ;
(4)在图3中,分别作出∠BAE和∠EDF的角平分线,交于点P,如图4.试用x、y表示∠P= (3x﹣y) .
【解答】(1)解:∵∠B=70°,∠C=40°,
∴∠BAC=180°﹣70°﹣40°=70°,
∵∠BAC的平分线交BC于点D,
∴∠BAD=∠BAC=×70°=35°,
在Rt△ABE中,∠BAE=90°﹣70°=20°,
∴∠EAD=∠BAD﹣∠BAE=35°﹣20°=15°,
(2)∵∠BAD=∠BAC=(180°﹣x﹣y),
∴∠AEB=180°﹣∠B﹣∠BAD=180°﹣x﹣(180°﹣x﹣y)=90°﹣x+y,
∴∠DFE=90°﹣∠AEB=90°﹣90°+x﹣y=(x﹣y).
故答案为(x﹣y).
(3)∵∠BAD=∠BAC=(180°﹣x﹣y),
∴∠AEB=180°﹣∠B﹣∠BAD=180°﹣x﹣(180°﹣x﹣y)=90°﹣x+y,
∴∠DEF=∠AEB=90°﹣x+y,
∴∠DFE=90°﹣∠DEF=90°﹣90°+x﹣y=(x﹣y).
故答案为(x﹣y).
(4)∵∠BAD=∠BAC=(180°﹣x﹣y),
∴∠PAF=(180°﹣x﹣y),
∴∠P=180°﹣45°﹣[180°﹣(180°﹣x﹣y)﹣x]=(3x﹣y).
故答案为(3x﹣y).
36.(2020春?雨花区校级期末)如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,CD⊥AB,垂足为D,延长CE与外角∠ABG的平分线交于点F.
(1)若∠A=60°,求∠DCE和∠F的度数;
(2)若∠A=n°(0<n<90),请直接写出∠DCE和∠F的度数(用含n的代数式表示);
(3)若△FCB高FH和∠DCB的角平分线交于点Q,在(2)的条件下求∠CQH的度数(用含n的代数式表示).
【解答】解:(1)∵CD⊥AB,∠A=60°,
∴∠ADC=90°,∠ACD=30°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE﹣∠ACD=45°﹣30°=15°,
∵∠ABG=∠A+∠ACB=150°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=75°,
∵∠FBG=∠F+∠FCB,
∴∠F=75°﹣45°=30°.
(2)∵CD⊥AB,∠A=n°,
∴∠ADC=90°,∠ACD=90°﹣n°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE﹣∠ACD=45°﹣90°+n°=n°﹣45°,
∵∠ABG=∠A+∠ACB=90°+n°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=45°+n°
∵∠FBG=∠F+∠FCB,
∴∠F=n°.
(3)如图,∵FH⊥CG,
∴∠FHC=90°,
∵∠A+∠ACD=90°,∠ACD+∠DCB=90°
∴∠A=∠DCB=n°,
∵CQ平分∠DCB,
∴∠QCH=n°,
∴∠CQH=90°﹣n°.
37.(2020春?新都区期末)如图1,∠MON=80°,点A、B在∠MON的两条边上运动,∠OAB与∠OBA的平分线交于点C.
(1)点A、B在运动过程中,∠ACB的大小会变吗?如果不会,求出∠ACB的度数;如果会,请说明理由.
(2)如图2,AD是∠MAB的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,∠E的大小会变吗?如果不会,求出∠E的度数;如果会,请说明理由.
(3)在(2)的条件下,若∠MON=n,请直接写出∠ACB= 90°+?n ;∠E= ?n .
【解答】解:(1)如图1中,
∵AC平分∠OABMCB平分∠OBA,
∴∠CAB=∠OAB,∠CBA=∠OBA,
∴∠ACB=180°﹣(∠CAB+∠CBA)=180°﹣(∠OAB+∠OBA)=180°﹣(180°﹣∠O)=90°+∠O,
∵∠O=80°,
∴∠ACB=90°+40°=130°.
(2)如图2中,由题意可以假设∠MAD=∠DAB=y,∠ABE=∠EBO=x.
则有,可得∠O,
∵∠O=80°,
∴∠E=40°.
(3)由(1)(2)可知,∠ACB=90°+?n,∠E=?n.
故答案为:90°+?n,?n
38.(2020春?清江浦区期末)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC度数.
思路点拨:
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可分别求出∠APE、∠CPE的度数,从而可求出∠APC的度数;
小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∠APC的度数;
小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∠APC的度数.
问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∠APC的度数为 110 °;
问题迁移:(1)如图5,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
【解答】解:小明的思路:如图2,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=180°﹣∠A=50°,∠CPE=180°﹣∠C=60°,
∴∠APC=50°+60°=110°,
故答案为:110;
(1)∠CPD=∠α+∠β,理由如下:
如图5,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)当P在BA延长线时,∠CPD=∠β﹣∠α;
理由:如图6,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;
当P在BO之间时,∠CPD=∠α﹣∠β.
理由:如图7,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.
_21?????????è?????(www.21cnjy.com)_
八下第一章三角形的初步知识培优习题精选
一.选择题(共19小题)
1.(2020春?雨花区期末)如图,已知CD和BE是△ABC的角平分线,∠A=60°,则∠BOC=( )
A.60° B.100° C.120° D.150°
2.(2020?雁塔区校级模拟)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F,交边BC于点E,连接DE.若∠ABC=40°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
3.(2020春?义乌市期末)如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G∥BC,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
4.(2020春?岱岳区期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠BAE=30°,∠CAD=20°,则∠B=( )
A.45° B.60° C.50° D.55°
5.(2020?苏家屯区一模)如图,Rt△ABC中,∠B=90°,∠A=55°,45°的直三角板DEF的锐角顶点D在斜边AC上,直角边DE∥BC,则∠FDC的度数为( )
A.10° B.15° C.20° D.25°
6.(2020春?徐州期中)如图,在△ABC中,点D、E分别为BC、AD的中点,EF=2FC,若△ABC的面积为12cm2,则△BEF的面积为( )
A.2cm2 B.3cm2 C.4cm2 D.5cm2
7.(2020春?江阴市期中)如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;
②∠ADC=∠GCD;
③CA平分∠BCG;
④∠DFB=∠CGE.
其中正确的结论是( )
A.②③ B.①②④ C.①③④ D.①②③④
8.(2020春?江阴市校级期中)如图,在△ABC中,点D在BC上,点E、F在AB上,点G在DF的延长线上,且∠B=∠DFB,∠G=∠DEG,若∠BEG=29°,则∠BDE的度数为( )
A.61° B.58° C.65.5° D.59.5°
9.(2020春?天心区期末)如图,一副直角三角板图示放置,点C在DF的延长线上,点A在边EF上,AB∥CD,∠ACB=∠EDF=90°,则∠CAF=( )
A.10° B.15° C.20° D.25°
10.(2020?浙江自主招生)如图,在四边形ABCD中,M,N分别是AB,CD的中点,AN,BN,DM,CM划分四边形所成7个区域的面积分别为S1,S2,S3,S4,S5,S6,S7,那么恒成立的关系式是( )
A.S2+S6=S4 B.S1+S7=S4 C.S2+S3=S4 D.S1+S6=S4
11.(2019秋?市中区校级期末)如图,有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ改变位置,但始终满足经过B、C两点.如果△ABC中∠A=52°,则∠ABX+∠ACX=( )
A.38° B.48° C.28° D.58°
12.(2019秋?义安区期末)如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
13.(2019秋?呼和浩特期末)图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
14.(2019秋?桥西区校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105° B.100° C.110° D.115°
15.(2019秋?邓州市期末)如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF B.AE=7cm C.EF平分AB D.AB⊥CF
16.(2020?平湖市二模)如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为( )
A. B. C. D.
17.(2020?开平区一模)用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,正确的作法有( )
A.1种 B.2种 C.3种 D.4种
18.(2020?中原区校级模拟)如图所示,在Rt△ABC中,∠C=90°,按以下步骤作图:
①以点A为圆心,以小于AC的长为半径作弧,分别交AC、AB于点M,N;
②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点O;
③作射线OA,交BC于点E,若CE=6,BE=10.
则AB的长为( )
A.11 B.12 C.18 D.20
19.(2020?朝阳区模拟)如图,Rt△ABC中,∠ACB=90°.
(1)以点C为圆心,以CB的长为半径画弧,交AB于点G,分别以点G,B为圆心,以大于GB的长为半径画弧,两弧交于点K,作射线CK;
(2)以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于点N,分别以点M,N为圆心,以大于MN的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E;
(3)过点D作DF⊥AB交AB的延长线于点F,连接CF.
根据以上操作过程及所作图形,有如下结论:
①CE=CD;
②BC=BE=BF;
③S四边形CDFB=CF?BD;
④∠BCF=∠BCE.
所有正确结论的序号为( )
A.①②③ B.①③ C.②④ D.③④
二.填空题(共10小题)
20.(2019秋?包河区期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为 .
21.(2019秋?滑县期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是 .
22.(2019秋?镇原县期末)如图,已知△ABC≌△A′BC′,AA′∥BC,∠ABC=70°,则∠CBC′= .
23.(2019春?滨湖区期中)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为
24.(2019秋?海州区期中)如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB= °.
25.(2018秋?阜南县期末)在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为 .
26.(2019秋?江都区期末)如图,在△PAB中,PA=PB,D、E、F分别是边PA,PB,AB上的点,且AD=BF,BE=AF,若∠DFE=40°,则∠P= °.
27.(2020春?武侯区期末)如图,在Rt△ACB中,∠C=90°,AB=2,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则△ABD的面积为 .
28.(2019秋?和平区期末)定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)图①是顶角为36°的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为36°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)图③是顶角为45°的等腰三角形,请你在图③中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数 .
(3)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,则x所有可能的值为 .
29.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
三.解答题(共10小题)
30.(2020春?浦东新区期末)已知线段a、b,作出条一线段,使它等于2a﹣b.(用直尺和圆规作图,不写作法,保留作图痕迹).
31.(2020春?南岸区期末)如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠B=70°,求∠C的度数;
(2)若AE=AC,AD平分∠BDE是否成立?请说明理由.
32.(2020春?南岗区校级期中)如图,在△ABC中,BD,CE分别是AC,AB边上的高,在BD上截取BF=AC,延长CE至点G使CG=AB,连接AF,AG.
(1)如图1,求证:AG=AF;
(2)如图2,若BD恰好平分∠ABC,过点G作GH⊥AC交CA的延长线于点H,请直接写出图中所有的全等三角形并用全等符号连接.
33.(2019秋?鲤城区校级期末)已知,在△ABC中,AC=BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM,BN于点D,E.
(1)如图1.若CD=CE.求∠ABE的大小;
(2)如图2.∠ABC=∠DEB=60°.求证:AD+DC=BE.
34.(2018秋?寿县期末)如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
35.(2020春?裕华区校级期末)(1)已知△ABC中,∠B>∠C,AD⊥BC于D,AE平分∠BAC,∠B=70°,∠C=40°,求∠DAE的度数.
(2)在图2中,∠B=x,∠C=y,其他条件不变,若把“AD⊥BC于D改为“F是AE上一点,FD⊥BC于D“,试用x、y表示∠DFE= :
(3)在图3中,若把(2)中的“点F在AE上“改为点F是AE延长线上一点”,其余条件不变,试用x、y表示∠DFE= ;
(4)在图3中,分别作出∠BAE和∠EDF的角平分线,交于点P,如图4.试用x、y表示∠P= .
36.(2020春?雨花区校级期末)如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,CD⊥AB,垂足为D,延长CE与外角∠ABG的平分线交于点F.
(1)若∠A=60°,求∠DCE和∠F的度数;
(2)若∠A=n°(0<n<90),请直接写出∠DCE和∠F的度数(用含n的代数式表示);
(3)若△FCB高FH和∠DCB的角平分线交于点Q,在(2)的条件下求∠CQH的度数(用含n的代数式表示).
37.(2020春?新都区期末)如图1,∠MON=80°,点A、B在∠MON的两条边上运动,∠OAB与∠OBA的平分线交于点C.
(1)点A、B在运动过程中,∠ACB的大小会变吗?如果不会,求出∠ACB的度数;如果会,请说明理由.
(2)如图2,AD是∠MAB的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,∠E的大小会变吗?如果不会,求出∠E的度数;如果会,请说明理由.
(3)在(2)的条件下,若∠MON=n,请直接写出∠ACB= ;∠E= .
38.(2020春?清江浦区期末)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC度数.
思路点拨:
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可分别求出∠APE、∠CPE的度数,从而可求出∠APC的度数;
小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∠APC的度数;
小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∠APC的度数.
问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∠APC的度数为 °;
问题迁移:(1)如图5,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
八下第一章三角形的初步知识培优习题精选
参考答案与试题解析
一.选择题(共19小题)
1.(2020春?雨花区期末)如图,已知CD和BE是△ABC的角平分线,∠A=60°,则∠BOC=( )
A.60° B.100° C.120° D.150°
【解答】解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵CD和BE是△ABC的角平分线,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)=60°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=120°,
故选:C.
2.(2020?雁塔区校级模拟)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F,交边BC于点E,连接DE.若∠ABC=40°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
【解答】解:∵∠B=40°,∠C=50°,
∴∠BAC=90°,
∵∠ABF=∠EBF,BF=BF,∠BFA=∠BFE=90°,
∴△BFA≌△BFE(ASA),
∴BA=BE,
∵BD=BD,
∴△BDA≌△BDE(SAS),
∴∠BED=∠BAD=90°,
∴∠CED=90°,
∴∠CDE=90°﹣50°=40°,
故选:B.
3.(2020春?义乌市期末)如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G∥BC,B'E∥FG,则∠C'FE的度数是( )
A. B.90°﹣ C.α﹣90° D.2α﹣180°
【解答】解:设∠ADB′=γ,∠AGC′=β,∠CEB′=y,∠C′FE=x,
∵B'D∥C'G,
∴γ+β=∠B+∠C=α,
∵EB′∥FG,
∴∠CFG=∠CEB′=y,
∴x+2y=180° ①,
∵γ+y=2∠B,β+x=2∠C,
∴γ+y+β+x=2α,
∴x+y=α②,
②×2﹣①可得x=2α﹣180°,
∴∠C′FE=2α﹣180°.
故选:D.
4.(2020春?岱岳区期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠BAE=30°,∠CAD=20°,则∠B=( )
A.45° B.60° C.50° D.55°
【解答】解:∵AE平分∠BAC,
∴∠BAE=∠CAE=30°,
∴∠EAD=∠EAC﹣∠DAC=30°﹣20°=10°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠AED=90°﹣∠EAD=80°,
∵∠AED=∠B+∠BAE,
∴∠B=80°﹣30°=50°,
故选:C.
5.(2020?苏家屯区一模)如图,Rt△ABC中,∠B=90°,∠A=55°,45°的直三角板DEF的锐角顶点D在斜边AC上,直角边DE∥BC,则∠FDC的度数为( )
A.10° B.15° C.20° D.25°
【解答】解:∵∠B=90°,∠A=55°,
∴∠C=35°,
∵DE∥BC,
∴∠C=∠EDC=35°,
∵∠EDF=45°,
∴∠CDF=∠EDF﹣∠EDC=45°﹣35°=10°,
故选:A.
6.(2020春?徐州期中)如图,在△ABC中,点D、E分别为BC、AD的中点,EF=2FC,若△ABC的面积为12cm2,则△BEF的面积为( )
A.2cm2 B.3cm2 C.4cm2 D.5cm2
【解答】解:∵D是BC的中点,
∴S△ABD=S△ADC(等底等高的三角形面积相等),
∵E是AD的中点,
∴S△ABE=S△BDE,S△ACE=S△CDE(等底等高的三角形面积相等),
∴S△ABE=S△DBE=S△DCE=S△AEC,
∴S△BEC=S△ABC=6cm2.
∵EF=2FC,
∴S△BEF=S△BCE,
∴S△BEF=S△BEC=4cm2.
故选:C.
7.(2020春?江阴市期中)如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;
②∠ADC=∠GCD;
③CA平分∠BCG;
④∠DFB=∠CGE.
其中正确的结论是( )
A.②③ B.①②④ C.①③④ D.①②③④
【解答】解:∵EG∥BC,
∴∠CEG=∠BCA,
∵CD平分∠ACB,
∴∠BCA=2∠DCB,
∴∠CEG=2∠DCB,故①正确,
∵CG⊥EG,
∴∠G=90°,
∴∠GCE+∠CEG=90°,
∵∠A=90°,
∴∠BCA+∠ABC=90°,
∵∠CEG=∠ACB,
∴∠ECG=∠ABC,
∵∠ADC=∠ABC+∠DCB,∠GCD=∠ECG+∠ACD,∠ACD=∠DCB,
∴∠ADC=∠GCD,故②正确,
假设AC平分∠BCG,则∠ECG=∠ECB=∠CEG,
∴∠ECG=∠CEG=45°,显然不符合题意,故③错误,
∵∠DFB=∠FCB+∠FBC=(∠ACB+∠ABC)=45°,∠CGE=45°,
∴∠DFB=∠CGE,故④正确,
故选:B.
8.(2020春?江阴市校级期中)如图,在△ABC中,点D在BC上,点E、F在AB上,点G在DF的延长线上,且∠B=∠DFB,∠G=∠DEG,若∠BEG=29°,则∠BDE的度数为( )
A.61° B.58° C.65.5° D.59.5°
【解答】解:设∠DEF=x,∠EDF=y,则∠DFB=∠B=x+y,∠BDF=180°﹣2x﹣2y,∠G=∠DEG=x+29°,
∵∠G+∠FEG=∠B+∠BDF,
∴x+29°+29°=x+y+180°﹣2x﹣2y,
∴2x+y=122°,
∴∠BDE=∠BDF+∠EDF=180°﹣2x﹣2y+y=180°﹣2x﹣y=58°,
故选:B.
9.(2020春?天心区期末)如图,一副直角三角板图示放置,点C在DF的延长线上,点A在边EF上,AB∥CD,∠ACB=∠EDF=90°,则∠CAF=( )
A.10° B.15° C.20° D.25°
【解答】解:∵AB∥CD,
∴∠BAC=∠ACD=30°,
∵∠AFD=∠CAF+∠ACF=45°,
∴∠CAF=45°﹣30°=15°,
故选:B.
10.(2020?浙江自主招生)如图,在四边形ABCD中,M,N分别是AB,CD的中点,AN,BN,DM,CM划分四边形所成7个区域的面积分别为S1,S2,S3,S4,S5,S6,S7,那么恒成立的关系式是( )
A.S2+S6=S4 B.S1+S7=S4 C.S2+S3=S4 D.S1+S6=S4
【解答】解:过A作AE⊥DC于E,过M作MH⊥DC于H,过B作BQ⊥DC于Q,
则AE∥MH∥BQ,
∵M为AB中点,
∴H为EQ中点,
即MH是梯形AEQB的中位线,
∴2MH=AE+BQ,
∵S3+S4+S6=S△MDC=×DC×MH,
S7+S6=S△BNC=×NC×BQ,
S1+S3=S△ADN=×DN×AE,
∵N为DC中点,
∴DN=CN,
∴S7+S6+S1+S3,
=×NC×BQ+×DN×AE,
=DN×(AE+BQ),
=DN×2MH,
=DN×MH,
=CD×MH,
∴S7+S6+S1+S3=S3+S4+S6,
∴S4=S1+S7;
故选:B.
11.(2019秋?市中区校级期末)如图,有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ改变位置,但始终满足经过B、C两点.如果△ABC中∠A=52°,则∠ABX+∠ACX=( )
A.38° B.48° C.28° D.58°
【解答】解:连接AX,
∵∠BXC=90°,
∴∠AXB+∠AXC=360°﹣∠BXC=270°,
∵∠A=52°,
∴∠BAX+∠CAX=52°,
∵∠ABX+∠BAX+∠AXB=180°,∠ACX+∠CAX+∠AXC=180°,
∴∠ABX+∠ACX=360°﹣270°﹣52°=38°,
故选:A.
12.(2019秋?义安区期末)如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=131°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
【解答】解:由折叠得:∠HOG=∠B,∠DOE=∠A,∠EOF=∠C,
∵∠A+∠B+∠C=180°,
∴∠HOG+∠DOE+∠EOF=180°,
∵∠1+∠2+∠HOG+∠DOE+∠EOF=360°,
∴∠1+∠2=180°,
∵∠1=131°,
∴∠2=180°﹣131°=49°,
故选:A.
13.(2019秋?呼和浩特期末)图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
【解答】解:观察图象可知△MNP≌△MFD.
故选:A.
14.(2019秋?桥西区校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105° B.100° C.110° D.115°
【解答】解:延长C′D交AB′于H.
∵△AEB≌△AEB′,
∴∠ABE=∠AB′E,
∵C′H∥EB′,
∴∠AHC′=∠AB′E,
∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,
∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:B.
15.(2019秋?邓州市期末)如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF B.AE=7cm C.EF平分AB D.AB⊥CF
【解答】解:∵EF⊥AC,∠ACB=90°,
∴∠FEC=∠ACB=90°,
∴∠F+∠FCE=∠FCE+∠BCF=90°,
∴∠F=∠BCF;故A选项正确;
在Rt△ACB与Rt△FEC中,,
∴Rt△ACB≌Rt△FEC(HL),
∴AC=EF=12,CE=BC=5cm,
∴AE=AC﹣CE=7cm,故B选项正确;
∵Rt△ACB≌Rt△FEC,
∴∠A=∠F,
∵∠ADE=∠EDF,
∴∠FED=∠AEF=90°,
∴AB⊥CF,故D选项正确;
∵∠AED=∠ACB,
∴DE∥BC,
∴==,
∴AD≠DB,
∴EF不平分AB,故C选项错误,
故选:C.
16.(2020?平湖市二模)如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为( )
A. B. C. D.
【解答】解:由作图可知,四边形ECFD是正方形,
∴DE=DF=CE=CF,∠DEC=∠DFC=90°,
∵S△ACB=S△ADC+S△CDB,
∴×AC×BC=×AC×DE+×BC×DF,
∴DE==,
故选:C.
17.(2020?开平区一模)用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,正确的作法有( )
A.1种 B.2种 C.3种 D.4种
【解答】解:(1)根据垂径定理作图的方法可知:
CD是Rt△ABC斜边AB上的高线,故作法正确;
(2)根据直径所对圆周角是直角的方法可知:
CD是Rt△ABC斜边AB上的高线,故作法正确;
(3)根据相交两圆的公共弦的性质可知:
CD是Rt△ABC斜边AB上的高线,故作法正确;
(4)无法证明CD是Rt△ABC斜边AB上的高线,故作法不正确;
综上所述:正确的作法有3种.
故选:C.
18.(2020?中原区校级模拟)如图所示,在Rt△ABC中,∠C=90°,按以下步骤作图:
①以点A为圆心,以小于AC的长为半径作弧,分别交AC、AB于点M,N;
②分别以点M,N为圆心,以大于MN的长为半径作弧,两弧相交于点O;
③作射线OA,交BC于点E,若CE=6,BE=10.
则AB的长为( )
A.11 B.12 C.18 D.20
【解答】解:过点E作DE⊥AB于点D,
由作图知AP平分∠BAC,
∵∠C=∠ADE=90°,
∴CE=DE=6,
∵BE=10,
∴BD=8,
∵AD=AD,CE=DE,
∴Rt△ACE≌Rt△ADE(HL),
∴AC=AD,
设AC=AD=x,
由AC2+BC2=AB2得x2+162=(x+8)2,
解得:x=6,即AC=12,
∵AB=20,
故选:D.
19.(2020?朝阳区模拟)如图,Rt△ABC中,∠ACB=90°.
(1)以点C为圆心,以CB的长为半径画弧,交AB于点G,分别以点G,B为圆心,以大于GB的长为半径画弧,两弧交于点K,作射线CK;
(2)以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于点N,分别以点M,N为圆心,以大于MN的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E;
(3)过点D作DF⊥AB交AB的延长线于点F,连接CF.
根据以上操作过程及所作图形,有如下结论:
①CE=CD;
②BC=BE=BF;
③S四边形CDFB=CF?BD;
④∠BCF=∠BCE.
所有正确结论的序号为( )
A.①②③ B.①③ C.②④ D.③④
【解答】解:如图,连接CF,交BD于点H,
由作图过程可知:
CE是BG的垂直平分线,BD是∠CBF的平分线,
设CE与AB交于点Q,
∴∠CQA=∠DFA=90°,
∴CQ∥DF,
∴∠CED=∠FDE,
∵BD是∠CBF的平分线,
∴∠CBD=∠FBD,
∵∠BCD=∠BFD=90°,
BD=BD,
∴△BCD≌△BFD(AAS),
∴∠CDB=∠FDB,
∴∠CDB=∠CED,
∴CE=CD,
所以①正确;
∵△BCD≌△BFD(AAS),
∴BC=BF,
但是BC≠BE,
∴②不正确;
∵S四边形CDFB=S△BCD+S△BFD
=BD?CH+BD?FH
=CF?BD.
∴③正确;
∵△BCE与△BCF不全等,
∴∠BCE≠∠BCF,
∴④不正确.
所以正确结论的序号为①③.
故选:B.
二.填空题(共10小题)
20.(2019秋?包河区期末)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为 70° .
【解答】解:∵△ABC≌△ADE,
∴AB=AD,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵∠EAC=40°,
∴∠BAD=40°,
∵AB=AD,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
故答案为:70°.
21.(2019秋?滑县期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是 180° .
【解答】解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个全等三角形,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
故答案为:180°
22.(2019秋?镇原县期末)如图,已知△ABC≌△A′BC′,AA′∥BC,∠ABC=70°,则∠CBC′= 40° .
【解答】解:∵AA′∥BC,
∴∠A′AB=∠ABC=70°,
∵△ABC≌△A′BC′,
∴BA=BA′,∠A′BC=∠ABC=70°,
∴∠A′AB=∠AA′B=70°,
∴∠A′BA=40°,
∴∠ABC′=30°,
∴∠CBC′=40°,
故答案为:40°.
23.(2019春?滨湖区期中)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为 48
【解答】解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48.
故答案为48.
24.(2019秋?海州区期中)如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠AED=105°,∠CAD=10°,∠B=50°,则∠EAB= 60 °.
【解答】解:∵△ABC≌△ADE,∠B=50°,
∴∠D=∠B=50°,∠EAD=∠CAB,
∵∠AED=105°,
∴∠EAD=180°﹣∠D﹣∠AED=25°,
∴∠CAB=25°,
∵∠CAD=10°,
∴∠EAB=∠EAD+∠DAC+∠CAB=25°+10°+25°=60°
25.(2018秋?阜南县期末)在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为 135° .
【解答】解:∵在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴∠4=∠2,
∵∠1+∠4=90°,
∴∠1+∠2=90°,
∵AE=DE,∠AED=90°,
∴∠3=45°,
∴∠1+∠2+∠3=135°,
故答案为:135°
26.(2019秋?江都区期末)如图,在△PAB中,PA=PB,D、E、F分别是边PA,PB,AB上的点,且AD=BF,BE=AF,若∠DFE=40°,则∠P= 100 °.
【解答】解:∵PA=PB,
∴∠A=∠B,
在△ADF和△BFE中,
,
∴△ADF≌△BFE(SAS),
∴∠ADF=∠BFE,
∵∠DFB=∠DFE+∠EFB=∠A+∠ADF,
∴∠A=∠DFE=40°,
∴∠P=180°﹣∠A﹣∠B=100°,
故答案为:100.
27.(2020春?武侯区期末)如图,在Rt△ACB中,∠C=90°,AB=2,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则△ABD的面积为 .
【解答】解:如图,过点D作DH⊥AB于H.
∵DC⊥BC,DH⊥AB,BD平分∠ABC,
∴DH=CD=1,
∴S△ABD=?AB?DH=×2×1=,
故答案为.
28.(2019秋?和平区期末)定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)图①是顶角为36°的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为36°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)图③是顶角为45°的等腰三角形,请你在图③中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数 90°、135°、45° .
(3)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,则x所有可能的值为 20°或40° .
【解答】解:
(1)在图②中用不同于图①的方法画出顶角为36°的等腰三角形的三分线;
(2)在图③中画出顶角为45°的等腰三角形的三分线.
每个等腰三角形顶角的度数为:90°、135°、45°.
故答案为:90°、135°、45°.
(3)如下图作△ABC,
①如图1:当AD=AE时,
∵2x+x=30+30,
∴x=20.
②如图2:当AD=DE时,
∵2x+x+30+30=180.
∴x=40.
所以x的所有可能的值为20°或40°.
故答案为20°或40°.
29.(2020春?雨花区期末)如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,下列说法正确的是 ③⑤⑥ .(填写正确的序号)
①DF=BE,②△ADF≌△ABE,③FA平分∠DFE,④AE平分∠FAB,⑤BE+DF=EF,⑥CF+CE>FD+EB.
【解答】解:延长EB到G,使BG=DF,连接AG,
∵AB⊥CB,AD⊥CD,
∴∠D=∠ABG=90°,
在△ADF和△ABG中
,
∴△ADF≌△ABG(SAS),
∴AF=AG,∠G=∠DFA,∠DAF=∠BAG,
∵∠EAF=70°,∠DAB=140°,
∴∠DAF+∠EAB=∠DAB﹣∠FAE=140°﹣70°=70°,
∴∠EAG=∠EAB+∠BAG=∠EAB+∠FAD=70°,
∴∠FAE=∠EAG=70°,
在△FAE和△GAE中
,
∴△FAE≌△GAE(SAS),
∴∠FEA=∠GEA,∠G=∠EFA,EF=EG,
∴EF=EB+DF,∠FAE≠∠EAB,故⑤正确,④错误;
∴∠G=∠EFA=∠DFA,即AF平分∠DFE,故③正确;
∵CF+CE>EF,EF=DF+BE,
∴CF+CE>DF+BE,故⑥正确;
根据已知不能推出△ADF≌△ABE,故①错误,②错误;
故答案为:③⑤⑥.
三.解答题(共10小题)
30.(2020春?浦东新区期末)已知线段a、b,作出条一线段,使它等于2a﹣b.(用直尺和圆规作图,不写作法,保留作图痕迹).
【解答】解:如图,线段OF即为所求.
31.(2020春?南岸区期末)如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠B=70°,求∠C的度数;
(2)若AE=AC,AD平分∠BDE是否成立?请说明理由.
【解答】解:(1)∵∠B=70°,AB=AD,
∴∠ADB=∠B=70°,
∵∠B+∠BAD+∠ADB=180°,
∴∠BAD=40°,
∵∠CAE=∠BAD,
∴∠CAE=40°,
∵AE∥BC,
∴∠C=∠CAE=40°;
(2)AD平分∠BDE,
理由是:∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS)
∴∠B=∠ADE,
∵∠B=∠ADB,
∴∠ADE=∠ADB,
即AD平分∠BDE.
32.(2020春?南岗区校级期中)如图,在△ABC中,BD,CE分别是AC,AB边上的高,在BD上截取BF=AC,延长CE至点G使CG=AB,连接AF,AG.
(1)如图1,求证:AG=AF;
(2)如图2,若BD恰好平分∠ABC,过点G作GH⊥AC交CA的延长线于点H,请直接写出图中所有的全等三角形并用全等符号连接.
【解答】证明:(1)∵BD、CE分别是AC、AB两条边上的高,
∴∠AEC=∠ADB=90°,
∴∠ABD+∠BAD=∠ACE+∠CAE=90°,
∴∠ABD=∠ACG,
在△AGC与△FAB中,,
∴△AGC≌△FAB(SAS),
∴AG=AF;
(2)图中全等三角形有△AGC≌△FAB,由得出△CGH≌△BAD,
由得出Rt△AGH≌Rt△AFD,△ABD≌△CBD;△CBD≌△GCH.
33.(2019秋?鲤城区校级期末)已知,在△ABC中,AC=BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM,BN于点D,E.
(1)如图1.若CD=CE.求∠ABE的大小;
(2)如图2.∠ABC=∠DEB=60°.求证:AD+DC=BE.
【解答】(1)解:如图1,延长AC交BN于点F,
∵AM∥BN,
∴∠DAF=∠AFB,
在△ADC和△FEC中,,
∴△ADC≌△FEC(AAS),
∴AC=FC,
∵AC=BC,
∴BC=AC=FC=AF,
∴△ABF是直角三角形,
∴∠ABE=90°;
(2)证明:如图2,在EB上截取EH=EC,连CH,
∵AC=BC,∠ABC=60°,
∴△ABC为等边三角形,
∵∠DEB=60°,
∴△CHE是等边三角形,
∴∠CHE=60°,∠HCE=60°,
∴∠BHC=120°,
∵AM∥BN,
∴∠ADC+∠BEC=180°,
∴∠ADC=120°,
∴∠DAC+∠DCA=60°,
又∵∠DCA+∠ACB+∠BCH+∠HCE=180°,
∴∠DCA+∠BCH=60°,
∴∠DAC=∠BCH,
在△DAC与△HCB中,,
∴△DAC≌△HCB(AAS),
∴AD=CH,DC=BH,
又∵CH=CE=HE,
∴BE=BH+HE=DC+AD,
即AD+DC=BE.
34.(2018秋?寿县期末)如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
【解答】解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
35.(2020春?裕华区校级期末)(1)已知△ABC中,∠B>∠C,AD⊥BC于D,AE平分∠BAC,∠B=70°,∠C=40°,求∠DAE的度数.
(2)在图2中,∠B=x,∠C=y,其他条件不变,若把“AD⊥BC于D改为“F是AE上一点,FD⊥BC于D“,试用x、y表示∠DFE= (x﹣y) :
(3)在图3中,若把(2)中的“点F在AE上“改为点F是AE延长线上一点”,其余条件不变,试用x、y表示∠DFE= (x﹣y) ;
(4)在图3中,分别作出∠BAE和∠EDF的角平分线,交于点P,如图4.试用x、y表示∠P= (3x﹣y) .
【解答】(1)解:∵∠B=70°,∠C=40°,
∴∠BAC=180°﹣70°﹣40°=70°,
∵∠BAC的平分线交BC于点D,
∴∠BAD=∠BAC=×70°=35°,
在Rt△ABE中,∠BAE=90°﹣70°=20°,
∴∠EAD=∠BAD﹣∠BAE=35°﹣20°=15°,
(2)∵∠BAD=∠BAC=(180°﹣x﹣y),
∴∠AEB=180°﹣∠B﹣∠BAD=180°﹣x﹣(180°﹣x﹣y)=90°﹣x+y,
∴∠DFE=90°﹣∠AEB=90°﹣90°+x﹣y=(x﹣y).
故答案为(x﹣y).
(3)∵∠BAD=∠BAC=(180°﹣x﹣y),
∴∠AEB=180°﹣∠B﹣∠BAD=180°﹣x﹣(180°﹣x﹣y)=90°﹣x+y,
∴∠DEF=∠AEB=90°﹣x+y,
∴∠DFE=90°﹣∠DEF=90°﹣90°+x﹣y=(x﹣y).
故答案为(x﹣y).
(4)∵∠BAD=∠BAC=(180°﹣x﹣y),
∴∠PAF=(180°﹣x﹣y),
∴∠P=180°﹣45°﹣[180°﹣(180°﹣x﹣y)﹣x]=(3x﹣y).
故答案为(3x﹣y).
36.(2020春?雨花区校级期末)如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,CD⊥AB,垂足为D,延长CE与外角∠ABG的平分线交于点F.
(1)若∠A=60°,求∠DCE和∠F的度数;
(2)若∠A=n°(0<n<90),请直接写出∠DCE和∠F的度数(用含n的代数式表示);
(3)若△FCB高FH和∠DCB的角平分线交于点Q,在(2)的条件下求∠CQH的度数(用含n的代数式表示).
【解答】解:(1)∵CD⊥AB,∠A=60°,
∴∠ADC=90°,∠ACD=30°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE﹣∠ACD=45°﹣30°=15°,
∵∠ABG=∠A+∠ACB=150°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=75°,
∵∠FBG=∠F+∠FCB,
∴∠F=75°﹣45°=30°.
(2)∵CD⊥AB,∠A=n°,
∴∠ADC=90°,∠ACD=90°﹣n°,
∵CF平分∠ACB,∠ACB=90°,
∴∠ACE=∠FCB=∠ACB=45°,
∴∠DCE=∠ACE﹣∠ACD=45°﹣90°+n°=n°﹣45°,
∵∠ABG=∠A+∠ACB=90°+n°,
∵BF平分∠ABG,
∴∠FBG=∠ABG=45°+n°
∵∠FBG=∠F+∠FCB,
∴∠F=n°.
(3)如图,∵FH⊥CG,
∴∠FHC=90°,
∵∠A+∠ACD=90°,∠ACD+∠DCB=90°
∴∠A=∠DCB=n°,
∵CQ平分∠DCB,
∴∠QCH=n°,
∴∠CQH=90°﹣n°.
37.(2020春?新都区期末)如图1,∠MON=80°,点A、B在∠MON的两条边上运动,∠OAB与∠OBA的平分线交于点C.
(1)点A、B在运动过程中,∠ACB的大小会变吗?如果不会,求出∠ACB的度数;如果会,请说明理由.
(2)如图2,AD是∠MAB的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,∠E的大小会变吗?如果不会,求出∠E的度数;如果会,请说明理由.
(3)在(2)的条件下,若∠MON=n,请直接写出∠ACB= 90°+?n ;∠E= ?n .
【解答】解:(1)如图1中,
∵AC平分∠OABMCB平分∠OBA,
∴∠CAB=∠OAB,∠CBA=∠OBA,
∴∠ACB=180°﹣(∠CAB+∠CBA)=180°﹣(∠OAB+∠OBA)=180°﹣(180°﹣∠O)=90°+∠O,
∵∠O=80°,
∴∠ACB=90°+40°=130°.
(2)如图2中,由题意可以假设∠MAD=∠DAB=y,∠ABE=∠EBO=x.
则有,可得∠O,
∵∠O=80°,
∴∠E=40°.
(3)由(1)(2)可知,∠ACB=90°+?n,∠E=?n.
故答案为:90°+?n,?n
38.(2020春?清江浦区期末)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC度数.
思路点拨:
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可分别求出∠APE、∠CPE的度数,从而可求出∠APC的度数;
小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∠APC的度数;
小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∠APC的度数.
问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∠APC的度数为 110 °;
问题迁移:(1)如图5,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
【解答】解:小明的思路:如图2,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=180°﹣∠A=50°,∠CPE=180°﹣∠C=60°,
∴∠APC=50°+60°=110°,
故答案为:110;
(1)∠CPD=∠α+∠β,理由如下:
如图5,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(2)当P在BA延长线时,∠CPD=∠β﹣∠α;
理由:如图6,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;
当P在BO之间时,∠CPD=∠α﹣∠β.
理由:如图7,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
