2.6 直角三角形-2.7 探索勾股定理培优习题精选(含解析)
文档属性
| 名称 | 2.6 直角三角形-2.7 探索勾股定理培优习题精选(含解析) |  | |
| 格式 | rar | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 08:17:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版八年级下2.6-2.7小节直角三角形与勾股定理
一.选择题(共15小题)
1.(2019秋?鞍山期末)如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )
A.90° B.20° C.45° D.70°
2.(2019秋?开州区期末)如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠A=25°,则∠ADE的大小为( )
A.40° B.50° C.65° D.75°
3.(2017秋?洪雅县期末)直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是( )
A.22.5° B.45° C.67.5° D.135°
4.(2019?朝阳)把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是( )
A.83° B.57° C.54° D.33°
5.(2020?赤峰)如图,Rt△ABC中,∠ACB=90°,AB=5,AC=3,把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C',则四边形ABC'A'的面积是( )
A.15 B.18 C.20 D.22
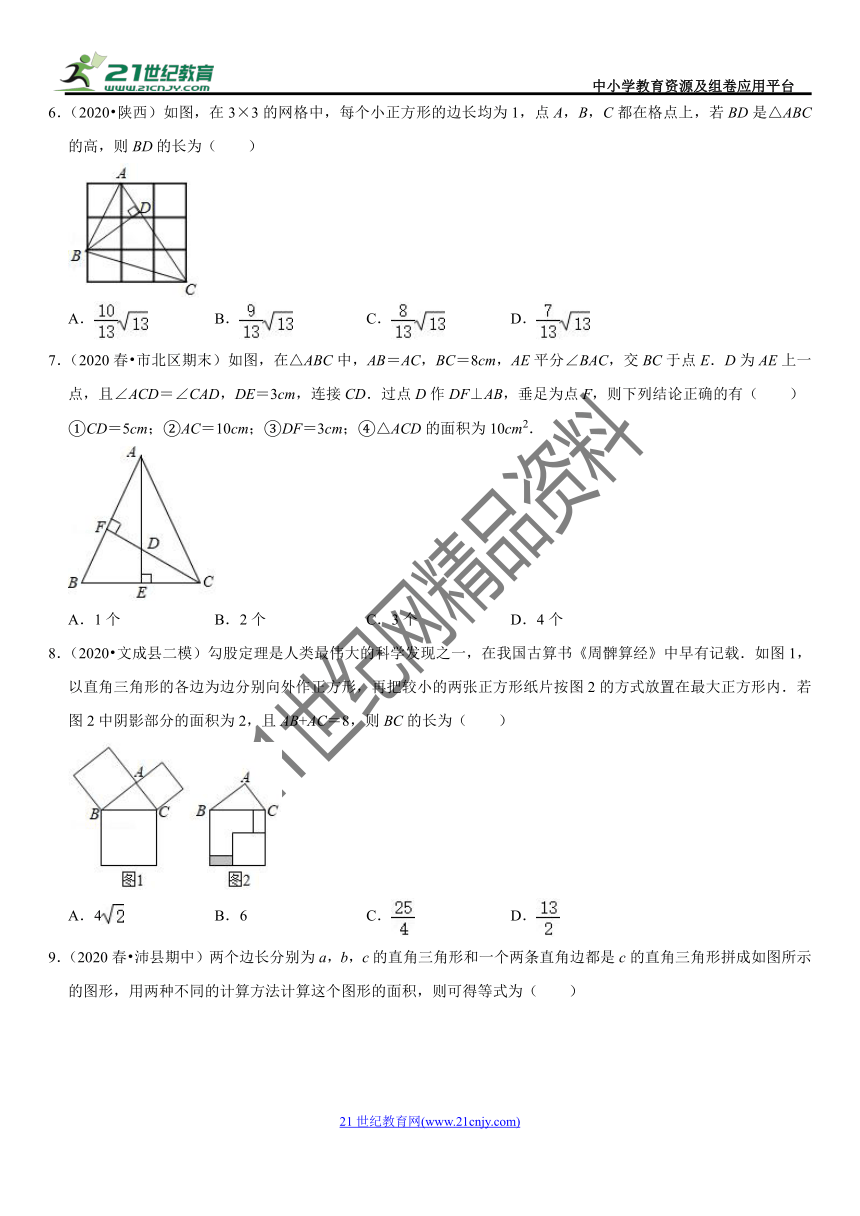
6.(2020?陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
7.(2020春?市北区期末)如图,在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,交BC于点E.D为AE上一点,且∠ACD=∠CAD,DE=3cm,连接CD.过点D作DF⊥AB,垂足为点F,则下列结论正确的有( )
①CD=5cm;②AC=10cm;③DF=3cm;④△ACD的面积为10cm2.
A.1个 B.2个 C.3个 D.4个
8.(2020?文成县二模)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A.4 B.6 C. D.
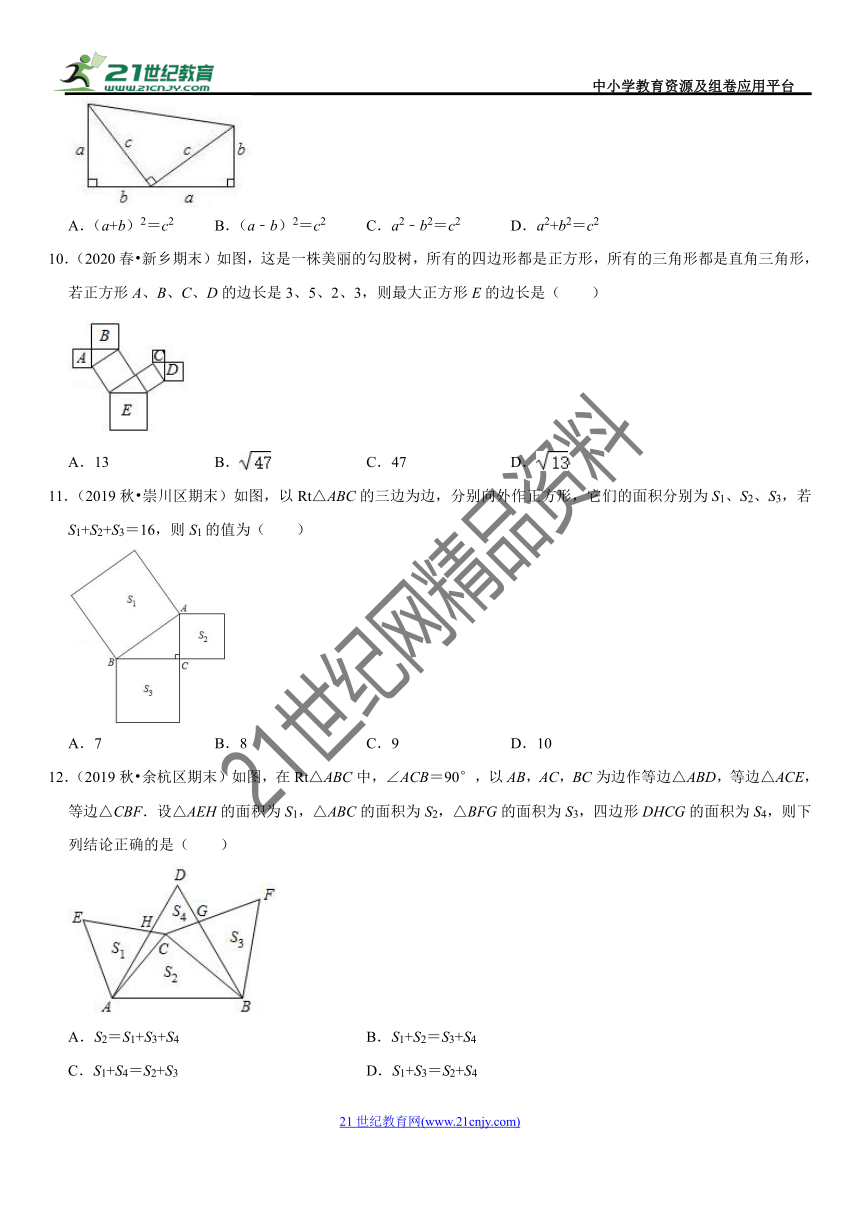
9.(2020春?沛县期中)两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2﹣b2=c2 D.a2+b2=c2
10.(2020春?新乡期末)如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是( )
A.13 B. C.47 D.
11.(2019秋?崇川区期末)如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=16,则S1的值为( )
A.7 B.8 C.9 D.10
12.(2019秋?余杭区期末)如图,在Rt△ABC中,∠ACB=90°,以AB,AC,BC为边作等边△ABD,等边△ACE,等边△CBF.设△AEH的面积为S1,△ABC的面积为S2,△BFG的面积为S3,四边形DHCG的面积为S4,则下列结论正确的是( )
A.S2=S1+S3+S4 B.S1+S2=S3+S4
C.S1+S4=S2+S3 D.S1+S3=S2+S4
13.(2019秋?偃师市期末)如图,在△ABC中,AB=AC=5,BC=6,P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
A.4.8 B.6 C.3.8 D.5
14.(2019秋?凤翔县期末)正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S2,…按此规律继续下去,则S5的值为( )
A. B. C. D.
15.(2019秋?仁寿县期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
二.填空题(共10小题)
16.(2020春?济阳区期末)如图,△ABC中,∠B=70°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为 .
17.(2020?哈尔滨模拟)在△ABC中,∠ACB=90°,∠A=40°,D为AB边上一点,若△ACD是等腰三角形,则∠BCD的度数为 .
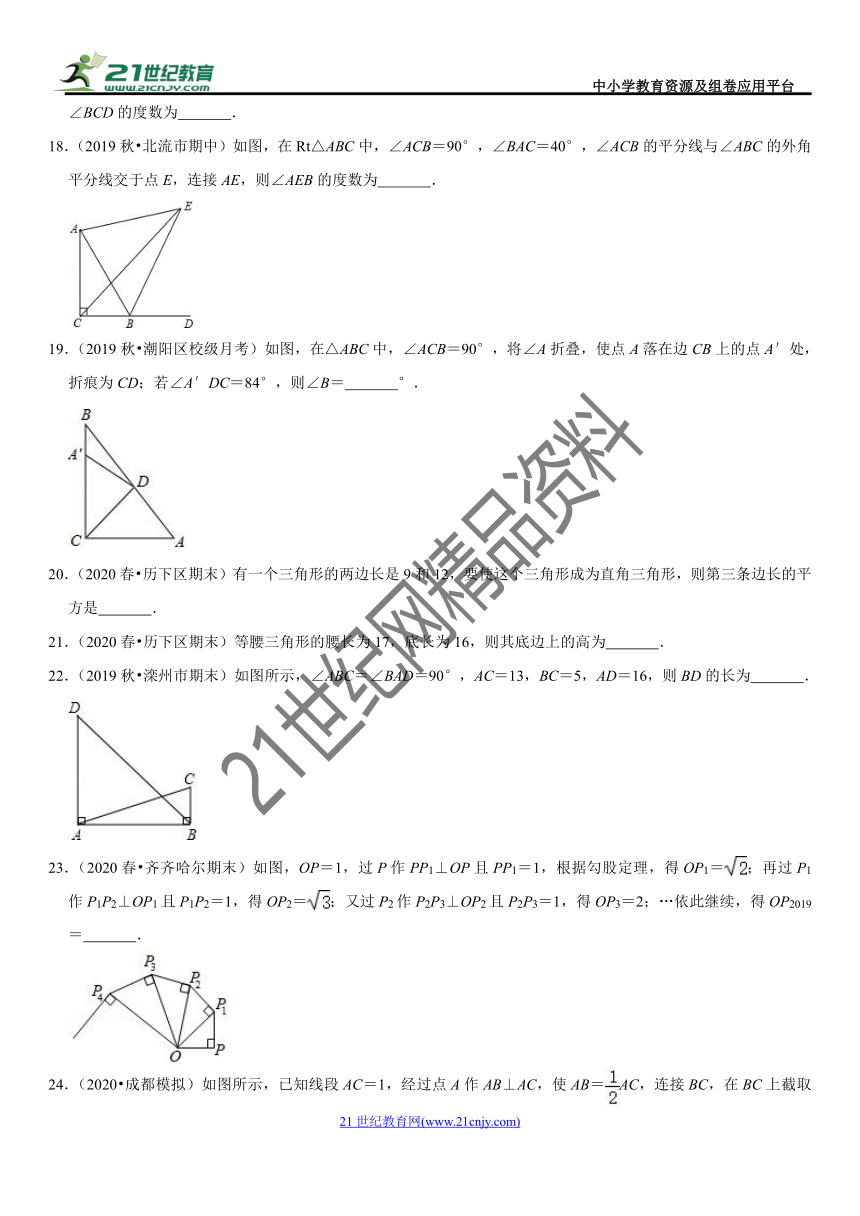
18.(2019秋?北流市期中)如图,在Rt△ABC中,∠ACB=90°,∠BAC=40°,∠ACB的平分线与∠ABC的外角平分线交于点E,连接AE,则∠AEB的度数为 .
19.(2019秋?潮阳区校级月考)如图,在△ABC中,∠ACB=90°,将∠A折叠,使点A落在边CB上的点A′处,折痕为CD;若∠A′DC=84°,则∠B= °.
20.(2020春?历下区期末)有一个三角形的两边长是9和12,要使这个三角形成为直角三角形,则第三条边长的平方是 .
21.(2020春?历下区期末)等腰三角形的腰长为17,底长为16,则其底边上的高为 .
22.(2019秋?滦州市期末)如图所示,∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,则BD的长为 .
23.(2020春?齐齐哈尔期末)如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1=;再过P1作P1P2⊥OP1且P1P2=1,得OP2=;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此继续,得OP2019= .
24.(2020?成都模拟)如图所示,已知线段AC=1,经过点A作AB⊥AC,使AB=AC,连接BC,在BC上截取BE=AB,在CA上截取CD=CE,则的值是 .
25.(2019秋?青羊区期末)如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5= .(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
三.解答题(共11小题)
26.(2019秋?南岸区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
27.(2019秋?雅安期末)如图,直线m∥n,△ABC的顶点B、C分别在直线n、m上,且∠ACB=90°,若∠1=50°.
求∠2的度数.
28.(2019秋?辛集市期末)如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.
(1)求∠ACE的度数.
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
29.(2020春?莱州市期末)如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
30.(2019秋?大连期末)如图,在△ABC中,∠B=90,∠C=30°,AB=6cm,BC=6cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
(1)点P运动到点A,t= (s);
(2)请你用含t的式子表示y.
31.(2019秋?北碚区期末)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
32.(2020春?越城区期中)如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.
(1)求AD的长;
(2)当△PDC的面积为15平方厘米时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得S△PMD=S△ABC?若存在,请求出t的值;若不存在,请说明理由.
33.(2019春?行唐县期末)勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b﹣a
S四边形ADCB=S△ADC+S△ABC=﹣b2+ab
S四边形ADCB=S△ADB+S△BCD=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明
如图(2)中∠DAB=90°,求证:a2+b2=c2
34.(2019春?沙坪坝区校级月考)如图①,在Rt△ABC中∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)根据勾股定理的知识,请直接写出a,b,c之间的数量关系;
(2)若正方形EFMN的面积为64,Rt△ABC的周长为18,求Rt△ABC的面积.
35.(2019秋?陇西县期中)分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=()2+1=2 S1=;
OA32=()2+1=3 S2=;
OA42=()2+1=4 S3=…
(1)请用含有n(n为正整数)的式子表示Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
2.6-2.7直角三角形与勾股定理
参考答案与试题解析
一.选择题(共15小题)
1.(2019秋?鞍山期末)如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )
A.90° B.20° C.45° D.70°
【解答】解:∵∠BAC=90°,
∴∠DAC+∠BAD=90°,
∵AD是△ABC的高,
∴∠ADB=∠BAD+∠B=90°,
∴∠DAC=∠B=20°,
故选:B.
2.(2019秋?开州区期末)如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠A=25°,则∠ADE的大小为( )
A.40° B.50° C.65° D.75°
【解答】解:∵在△ABC中,∠ACB=90°,∠A=25°,
∴∠B=180°﹣90°﹣25°=65°,
根据折叠可得∠CED=65°,
∴∠ADE=65°﹣25°=40°,
故选:A.
3.(2017秋?洪雅县期末)直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是( )
A.22.5° B.45° C.67.5° D.135°
【解答】解:
设∠B=x°,则∠A=3x°,
由直角三角形的性质可得∠A+∠B=90°,
∴x+3x=90,解得x=22.5,
∴∠B=22.5°,
故选:A.
4.(2019?朝阳)把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是( )
A.83° B.57° C.54° D.33°
【解答】解:过点C作CF∥AB,
∴∠BCF=∠B=25°.
又AB∥DE,
∴CF∥DE.
∴∠FCE=∠E=90°﹣∠D=90°﹣58°=32°.
∴∠BCE=∠BCF+∠FCE=25°+32°=57°.
故选:B.
5.(2020?赤峰)如图,Rt△ABC中,∠ACB=90°,AB=5,AC=3,把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C',则四边形ABC'A'的面积是( )
A.15 B.18 C.20 D.22
【解答】解:∵把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C',
∴A′B′=AB=5,A′C′=AC=3,∠A′C′B′=∠ACB=90°,A′A=CC′=3,
∴B′C′==4,AC∥A′C′,
∴四边形ACC′A′是矩形,
∴四边形ABC'A'的面积=(AA′+BC′)?AC=(3+4+3)×3=15,
故选:A.
6.(2020?陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
【解答】解:由勾股定理得:AC==,
∵S△ABC=3×3﹣=3.5,
∴,
∴,
∴BD=,
故选:D.
7.(2020春?市北区期末)如图,在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,交BC于点E.D为AE上一点,且∠ACD=∠CAD,DE=3cm,连接CD.过点D作DF⊥AB,垂足为点F,则下列结论正确的有( )
①CD=5cm;②AC=10cm;③DF=3cm;④△ACD的面积为10cm2.
A.1个 B.2个 C.3个 D.4个
【解答】解:①∵在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,
∴AE⊥BC,BE=CE=4cm,
在Rt△DEC中,CD==5cm,故①正确;
②∵∠ACD=∠CAD,
∴AD=CD=5cm,
∴AE=8cm,
在Rt△AEC中,AC==4cm,故②错误;
③∵∠DAF=∠BAE,∠AFD=∠AEB,
∴△DAF∽△BAE,
∴DF:AD=BE:AB,即DF:5=4:4,
解得DF=.
故DF=cm,故③错误;
④△ACD的面积为5×4÷2=10cm2,故④正确.
故选:B.
8.(2020?文成县二模)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A.4 B.6 C. D.
【解答】解:设AC=a,AB=b,BC=c,则a+b=8,c2=a2+b2,HG=c﹣b,DG=c﹣a,
则阴影部分的面积S=HG?DG=(c﹣b)(c﹣a)=2,
∵(a+b)2=a2+b2+2ab=64,
∴ab=32﹣,
∴S=c2﹣c(a+b)+ab=c2﹣8c+32﹣=2,
解得c1=6,c2=10(舍去).
故选:B.
9.(2020春?沛县期中)两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2﹣b2=c2 D.a2+b2=c2
【解答】解:根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:D.
10.(2020春?新乡期末)如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是( )
A.13 B. C.47 D.
【解答】解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:
x2=32+52=34;
y2=22+32=13;
z2=x2+y2=47;
即最大正方形E的面积为:z2=47,边长为z=.
故选:B.
11.(2019秋?崇川区期末)如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=16,则S1的值为( )
A.7 B.8 C.9 D.10
【解答】解:∵由勾股定理得:AC2+BC2=AB2,
∴S3+S2=S1,
∵S1+S2+S3=16,
∴2S1=16,
∴S1=8,
故选:B.
12.(2019秋?余杭区期末)如图,在Rt△ABC中,∠ACB=90°,以AB,AC,BC为边作等边△ABD,等边△ACE,等边△CBF.设△AEH的面积为S1,△ABC的面积为S2,△BFG的面积为S3,四边形DHCG的面积为S4,则下列结论正确的是( )
A.S2=S1+S3+S4 B.S1+S2=S3+S4
C.S1+S4=S2+S3 D.S1+S3=S2+S4
【解答】解:设AC=a,BC=b,AB=c,
∵△ABD,△ACE,△CBF都是等边三角形,
∴,,.
∵∠ACB=90°,
∴a2+b2=c2.
∴,
即S△ACE+S△BCF=S△ABD.
∴S1+S3=S2+S4.
故选:D.
13.(2019秋?偃师市期末)如图,在△ABC中,AB=AC=5,BC=6,P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
A.4.8 B.6 C.3.8 D.5
【解答】解:过A点作AF⊥BC于F,连结AP,如图.
∵△ABC中,AB=AC=5,BC=6,
∴BF=FC=BC=3,
∴△ABF中,AF===4.
∵S△ABC=S△ABP+S△ACP,
∴×6×4=×5×PD+×5×PE,
∴12=×5×(PD+PE),
PD+PE=4.8.
故选:A.
14.(2019秋?凤翔县期末)正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S2,…按此规律继续下去,则S5的值为( )
A. B. C. D.
【解答】解:在图中标上字母E,如图所示.
∵正方形ABCD的边长为1,△CDE为等腰直角三角形,
∴DE2+CE2=CD2,DE=CE,
∴S2+S2=S1.
观察,发现规律:S1=12=1,S2=S1=,S3=S2=,S4=S3=,…,
∴Sn=()n﹣1.
当n=5时,S5=()5﹣1=()4,
故选:A.
15.(2019秋?仁寿县期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
【解答】解:由勾股定理得,正方形F的面积=正方形A的面积+正方形B的面积=32+52=34,
同理,正方形G的面积=正方形C的面积+正方形D的面积=22+32=13,
∴正方形E的面积=正方形F的面积+正方形G的面积=47,
故选:D.
二.填空题(共10小题)
16.(2020春?济阳区期末)如图,△ABC中,∠B=70°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为 80°或140°或10° .
【解答】解:如图,有三种情形:
①当AC=AD时,∵△ABC中,∠B=70°,∠ACB=90°,
∴∠CAB=20°,
∵AC=AD,
∴∠ADC=∠DCA=(180°﹣∠CAB)=80°;
②当CD′=AD′时,
∵∠CAB=20°,
∴∠D′CA=∠CAB=20°,
∴∠AD′C=180°﹣20°﹣20°=140°.
③当AC=AD″时,则∠AD″C=∠ACD″,
∵∠CAB=20°,∠AD″C+∠ACD″=∠CAB,
∴∠AD″C=10°,
故答案为:80°或140°或10°.
17.(2020?哈尔滨模拟)在△ABC中,∠ACB=90°,∠A=40°,D为AB边上一点,若△ACD是等腰三角形,则∠BCD的度数为 20°或50° .
【解答】解:如图,
当AC=AD时,∠ACD=∠ADC=(180°﹣40°)=70°,
∴∠BCD=90°﹣∠ACD=20°.
当CD′=AD′时,∠D′CA=∠A=40°,
∴∠BCD′=90°﹣40°=50°,
故答案为20°或50°.
18.(2019秋?北流市期中)如图,在Rt△ABC中,∠ACB=90°,∠BAC=40°,∠ACB的平分线与∠ABC的外角平分线交于点E,连接AE,则∠AEB的度数为 45° .
【解答】解:作EF⊥AC交CA的延长线于F,EG⊥AB于G,EH⊥BC交CB的延长线于H,
∵CE平分∠ACB,BE平分∠ABD,
∴EF=EH,EG=EH,
∴EF=EF,又EF⊥AC,EG⊥AB,
∴AE平分∠FAG,
∵∠CAB=40°,
∴∠BAF=140°,
∴∠EAB=70°,
∵∠ACB=90°,∠CAB=40°,
∴∠ABC=50°,
∴∠ABH=130°,又BE平分∠ABD,
∴∠ABE=65°,
∴∠AEB=180°﹣∠EAB﹣∠ABE=45°,
故答案为:45°.
19.(2019秋?潮阳区校级月考)如图,在△ABC中,∠ACB=90°,将∠A折叠,使点A落在边CB上的点A′处,折痕为CD;若∠A′DC=84°,则∠B= 39 °.
【解答】解:∵△CDA′与△CDA关于CD成轴对称,
∴∠ADC=∠A′DC=84°,
∵∠ACB=90°,
∴∠DCA=∠DCB=45°,
∵∠CDA=∠B+∠DCB,
∴∠B=84°﹣45°=39°
故答案为:39.
20.(2020春?历下区期末)有一个三角形的两边长是9和12,要使这个三角形成为直角三角形,则第三条边长的平方是 225或63 .
【解答】解:当第三边是斜边时,第三边的长的平方是:92+122=225;
当第三边是直角边时,第三边长的平方是:122﹣92=63;
故答案是:225或63.
21.(2020春?历下区期末)等腰三角形的腰长为17,底长为16,则其底边上的高为 15 .
【解答】解:如图:
AB=AC=17,BC=16.
△ABC中,AB=AC,AD⊥BC;
则BD=DC=BC=8;
Rt△ABD中,AB=17,BD=8;
由勾股定理,得:AD=.
故答案为:15.
22.(2019秋?滦州市期末)如图所示,∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,则BD的长为 20 .
【解答】解:∵∠ABC=90°,AC=13,BC=5,
∴AB==12,
又∵∠BAD=90°,AD=16,
∴BD==20,
故答案为:20.
23.(2020春?齐齐哈尔期末)如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1=;再过P1作P1P2⊥OP1且P1P2=1,得OP2=;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此继续,得OP2019= 2 .
【解答】解:由勾股定理得:OP1=,OP2=;OP3=2;
OP4==;
依此类推可得OPn=,
∴OP2019==2.
故答案为:2.
24.(2020?成都模拟)如图所示,已知线段AC=1,经过点A作AB⊥AC,使AB=AC,连接BC,在BC上截取BE=AB,在CA上截取CD=CE,则的值是 .
【解答】解:设CD=a,则CE=a,
∵AC=1,AB=AC,
∴AB=,
∵BE=AB,
∴BE=,
∴BC=a+,
在Rt△ABC中,AC2+BA2=BC2,
∴,
解得,a=﹣或a=﹣(舍去),
∴AD=1﹣a=,
∴=.
故答案为:.
25.(2019秋?青羊区期末)如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5= 5 .(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
【解答】解:如图,连接MQ,作MG⊥EC于G,设PC交BM于TMN交EC于Q.
∵∠ABM=∠CBQ=90°,
∴∠ABC=∠MBQ,
∵BA=BM,BC=BQ,
∴△ABC≌△MBQ(SAS),
∴∠ACB=∠BQM=90°,
∵∠PQB=90°,
∴M,P,Q共线,
∵四边形CGMP是矩形,
∴MG=PC=BC,
∵∠BCT=∠MGQ=90°,∠BTC+∠CBT=90°,∠BQM+∠CBT=90°,
∴∠MQG=∠BTC,
∴△MGQ≌△BCT(AAS),
∴MQ=BT,
∵MN=BM,
∴NQ=MT,
∵∠MQG=∠BTC,
∴∠NQE=∠MTP,
∵∠E=∠MPT=90°,
则△NQE≌MTP(AAS),
∴S1+S5=S3=5.
故答案为:5.
三.解答题(共11小题)
26.(2019秋?南岸区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
【解答】解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=36°,
∴∠ABC=90°﹣∠A=54°,
∴∠CBD=126°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=63°;
(2)∵∠ACB=90°,∠CBE=63°,
∴∠CEB=90°﹣63°=27°.
又∵∠F=27°,
∴∠F=∠CEB=27°,
∴DF∥BE
27.(2019秋?雅安期末)如图,直线m∥n,△ABC的顶点B、C分别在直线n、m上,且∠ACB=90°,若∠1=50°.
求∠2的度数.
【解答】解:∵m∥n
∴∠ECB=∠1=50°,
又∵∠ACB=∠BCE+∠ACE=90°,
∴∠ACE=40°,
又∵∠ACE+∠2=180°
∴∠2=140°.
28.(2019秋?辛集市期末)如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.
(1)求∠ACE的度数.
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
【解答】解:(1)∵△ABC中,∠A=30°,∠B=60°,
∴∠ACB=180°﹣30°﹣60°=90°,
又∵CF平分∠ACB,
∴∠ACE=∠ACB=45°;
(2)∵CD⊥AB,∠B=60°,
∴∠BCD=90°﹣60°=30°,
又∵∠BCE=∠ACE=45°,
∴∠DCF=∠BCE﹣∠BCD=15°,
又∵∠CDF=75°,
∴∠CFD=180°﹣75°﹣15°=90°,
∴△CFD是直角三角形.
29.(2020春?莱州市期末)如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
【解答】证明:∵△ABC≌△DBE,
∴BE=BC,AC=ED;
连接EC.则△BCE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
在Rt△DCE中,
DC2+CE2=DE2,
∴DC2+BE2=AC2.
30.(2019秋?大连期末)如图,在△ABC中,∠B=90,∠C=30°,AB=6cm,BC=6cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
(1)点P运动到点A,t= 2 (s);
(2)请你用含t的式子表示y.
【解答】解:(1)点P运动到点A,t=6÷3=2(s);
故答案为:2.
(2)当0<t<2时,y=S△BPQ=?BQ?BP=?3t?t=t2,
即y=t2;
当t≥2时,作PH⊥BC于H,如图所示:
y=S△BPQ=?BQ?HP=×t×(18﹣3t)=﹣t2+t,
即y=﹣t2+t.
31.(2019秋?北碚区期末)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
【解答】(1)解:(1)BQ=2×2=4cm,
BP=AB﹣AP=8﹣2×1=6cm,
∵∠B=90°,
PQ===2(cm);
(2)解:根据题意得:BQ=BP,
即2t=8﹣t,
解得:t=;
即出发时间为秒时,△PQB是等腰三角形;
(3)解:分三种情况:
①当CQ=BQ时,如图1所示:
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
过B点作BE⊥AC于点E,
则BE===4.8(cm)
∴CE==3.6cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.
32.(2020春?越城区期中)如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.
(1)求AD的长;
(2)当△PDC的面积为15平方厘米时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得S△PMD=S△ABC?若存在,请求出t的值;若不存在,请说明理由.
【解答】解:(1)∵AB=AC=13,AD⊥BC,
∴BD=CD=5cm,且∠ADB=90°,
∴AD2=AC2﹣CD2
∴AD=12cm.
(2)AP=t,PD=12﹣t,
又∵由△PDM面积为PD×DC=15,
解得PD=6,∴t=6.
(3)假设存在t,
使得S△PMD=S△ABC.
①若点M在线段CD上,
即 时,PD=12﹣t,DM=5﹣2t,
由S△PMD=S△ABC,
即 ,
2t2﹣29t+50=0
解得t1=12.5(舍去),t2=2.(2分)
②若点M在射线DB上,即 .
由S△PMD=S△ABC
得 ,
2t2﹣29t+70=0
解得 ,.(2分)
综上,存在t的值为2或 或 ,使得S△PMD=S△ABC.(1分)
33.(2019春?行唐县期末)勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b﹣a
S四边形ADCB=S△ADC+S△ABC=﹣b2+ab
S四边形ADCB=S△ADB+S△BCD=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明
如图(2)中∠DAB=90°,求证:a2+b2=c2
【解答】证明:连结BD,过点B作DE边上的高BF,则BF=b﹣a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b﹣a),
∴ab+b2+ab=ab+c2+a(b﹣a),
∴a2+b2=c2.
34.(2019春?沙坪坝区校级月考)如图①,在Rt△ABC中∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)根据勾股定理的知识,请直接写出a,b,c之间的数量关系;
(2)若正方形EFMN的面积为64,Rt△ABC的周长为18,求Rt△ABC的面积.
【解答】解:(1)由勾股定理得,a2+b2=c2;
(2)∵正方形EFMN的面积为64,
∴c2=64,即c=8,
∵Rt△ABC的周长为18,
∴a+b+c=18,
∴a+b=10,
则Rt△ABC的面积=ab
=[(a+b)2﹣(a2+b2)]
=9.
35.(2019秋?陇西县期中)分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=()2+1=2 S1=;
OA32=()2+1=3 S2=;
OA42=()2+1=4 S3=…
(1)请用含有n(n为正整数)的式子表示Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
【解答】解:(1)+1=n+1
Sn=(n是正整数);
故答案是:;
(2)∵OA12=1,
OA22=()2+1=2,
OA32=()2+1=3,
OA42=()2+1=4,
∴OA12=,
OA2=,
OA3=,…
∴OA10=;
故答案是:;
(3)S12+S22+S32+…+S102
=()2+()2+()2+…+()2
=(1+2+3+…+10)
=.
_21?????????è?????(www.21cnjy.com)_
浙教版八年级下2.6-2.7小节直角三角形与勾股定理
一.选择题(共15小题)
1.(2019秋?鞍山期末)如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )
A.90° B.20° C.45° D.70°
2.(2019秋?开州区期末)如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠A=25°,则∠ADE的大小为( )
A.40° B.50° C.65° D.75°
3.(2017秋?洪雅县期末)直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是( )
A.22.5° B.45° C.67.5° D.135°
4.(2019?朝阳)把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是( )
A.83° B.57° C.54° D.33°
5.(2020?赤峰)如图,Rt△ABC中,∠ACB=90°,AB=5,AC=3,把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C',则四边形ABC'A'的面积是( )
A.15 B.18 C.20 D.22
6.(2020?陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
7.(2020春?市北区期末)如图,在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,交BC于点E.D为AE上一点,且∠ACD=∠CAD,DE=3cm,连接CD.过点D作DF⊥AB,垂足为点F,则下列结论正确的有( )
①CD=5cm;②AC=10cm;③DF=3cm;④△ACD的面积为10cm2.
A.1个 B.2个 C.3个 D.4个
8.(2020?文成县二模)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A.4 B.6 C. D.
9.(2020春?沛县期中)两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2﹣b2=c2 D.a2+b2=c2
10.(2020春?新乡期末)如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是( )
A.13 B. C.47 D.
11.(2019秋?崇川区期末)如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=16,则S1的值为( )
A.7 B.8 C.9 D.10
12.(2019秋?余杭区期末)如图,在Rt△ABC中,∠ACB=90°,以AB,AC,BC为边作等边△ABD,等边△ACE,等边△CBF.设△AEH的面积为S1,△ABC的面积为S2,△BFG的面积为S3,四边形DHCG的面积为S4,则下列结论正确的是( )
A.S2=S1+S3+S4 B.S1+S2=S3+S4
C.S1+S4=S2+S3 D.S1+S3=S2+S4
13.(2019秋?偃师市期末)如图,在△ABC中,AB=AC=5,BC=6,P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
A.4.8 B.6 C.3.8 D.5
14.(2019秋?凤翔县期末)正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S2,…按此规律继续下去,则S5的值为( )
A. B. C. D.
15.(2019秋?仁寿县期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
二.填空题(共10小题)
16.(2020春?济阳区期末)如图,△ABC中,∠B=70°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为 .
17.(2020?哈尔滨模拟)在△ABC中,∠ACB=90°,∠A=40°,D为AB边上一点,若△ACD是等腰三角形,则∠BCD的度数为 .
18.(2019秋?北流市期中)如图,在Rt△ABC中,∠ACB=90°,∠BAC=40°,∠ACB的平分线与∠ABC的外角平分线交于点E,连接AE,则∠AEB的度数为 .
19.(2019秋?潮阳区校级月考)如图,在△ABC中,∠ACB=90°,将∠A折叠,使点A落在边CB上的点A′处,折痕为CD;若∠A′DC=84°,则∠B= °.
20.(2020春?历下区期末)有一个三角形的两边长是9和12,要使这个三角形成为直角三角形,则第三条边长的平方是 .
21.(2020春?历下区期末)等腰三角形的腰长为17,底长为16,则其底边上的高为 .
22.(2019秋?滦州市期末)如图所示,∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,则BD的长为 .
23.(2020春?齐齐哈尔期末)如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1=;再过P1作P1P2⊥OP1且P1P2=1,得OP2=;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此继续,得OP2019= .
24.(2020?成都模拟)如图所示,已知线段AC=1,经过点A作AB⊥AC,使AB=AC,连接BC,在BC上截取BE=AB,在CA上截取CD=CE,则的值是 .
25.(2019秋?青羊区期末)如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5= .(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
三.解答题(共11小题)
26.(2019秋?南岸区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
27.(2019秋?雅安期末)如图,直线m∥n,△ABC的顶点B、C分别在直线n、m上,且∠ACB=90°,若∠1=50°.
求∠2的度数.
28.(2019秋?辛集市期末)如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.
(1)求∠ACE的度数.
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
29.(2020春?莱州市期末)如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
30.(2019秋?大连期末)如图,在△ABC中,∠B=90,∠C=30°,AB=6cm,BC=6cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
(1)点P运动到点A,t= (s);
(2)请你用含t的式子表示y.
31.(2019秋?北碚区期末)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
32.(2020春?越城区期中)如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.
(1)求AD的长;
(2)当△PDC的面积为15平方厘米时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得S△PMD=S△ABC?若存在,请求出t的值;若不存在,请说明理由.
33.(2019春?行唐县期末)勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b﹣a
S四边形ADCB=S△ADC+S△ABC=﹣b2+ab
S四边形ADCB=S△ADB+S△BCD=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明
如图(2)中∠DAB=90°,求证:a2+b2=c2
34.(2019春?沙坪坝区校级月考)如图①,在Rt△ABC中∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)根据勾股定理的知识,请直接写出a,b,c之间的数量关系;
(2)若正方形EFMN的面积为64,Rt△ABC的周长为18,求Rt△ABC的面积.
35.(2019秋?陇西县期中)分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=()2+1=2 S1=;
OA32=()2+1=3 S2=;
OA42=()2+1=4 S3=…
(1)请用含有n(n为正整数)的式子表示Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
2.6-2.7直角三角形与勾股定理
参考答案与试题解析
一.选择题(共15小题)
1.(2019秋?鞍山期末)如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )
A.90° B.20° C.45° D.70°
【解答】解:∵∠BAC=90°,
∴∠DAC+∠BAD=90°,
∵AD是△ABC的高,
∴∠ADB=∠BAD+∠B=90°,
∴∠DAC=∠B=20°,
故选:B.
2.(2019秋?开州区期末)如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠A=25°,则∠ADE的大小为( )
A.40° B.50° C.65° D.75°
【解答】解:∵在△ABC中,∠ACB=90°,∠A=25°,
∴∠B=180°﹣90°﹣25°=65°,
根据折叠可得∠CED=65°,
∴∠ADE=65°﹣25°=40°,
故选:A.
3.(2017秋?洪雅县期末)直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是( )
A.22.5° B.45° C.67.5° D.135°
【解答】解:
设∠B=x°,则∠A=3x°,
由直角三角形的性质可得∠A+∠B=90°,
∴x+3x=90,解得x=22.5,
∴∠B=22.5°,
故选:A.
4.(2019?朝阳)把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是( )
A.83° B.57° C.54° D.33°
【解答】解:过点C作CF∥AB,
∴∠BCF=∠B=25°.
又AB∥DE,
∴CF∥DE.
∴∠FCE=∠E=90°﹣∠D=90°﹣58°=32°.
∴∠BCE=∠BCF+∠FCE=25°+32°=57°.
故选:B.
5.(2020?赤峰)如图,Rt△ABC中,∠ACB=90°,AB=5,AC=3,把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C',则四边形ABC'A'的面积是( )
A.15 B.18 C.20 D.22
【解答】解:∵把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C',
∴A′B′=AB=5,A′C′=AC=3,∠A′C′B′=∠ACB=90°,A′A=CC′=3,
∴B′C′==4,AC∥A′C′,
∴四边形ACC′A′是矩形,
∴四边形ABC'A'的面积=(AA′+BC′)?AC=(3+4+3)×3=15,
故选:A.
6.(2020?陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
【解答】解:由勾股定理得:AC==,
∵S△ABC=3×3﹣=3.5,
∴,
∴,
∴BD=,
故选:D.
7.(2020春?市北区期末)如图,在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,交BC于点E.D为AE上一点,且∠ACD=∠CAD,DE=3cm,连接CD.过点D作DF⊥AB,垂足为点F,则下列结论正确的有( )
①CD=5cm;②AC=10cm;③DF=3cm;④△ACD的面积为10cm2.
A.1个 B.2个 C.3个 D.4个
【解答】解:①∵在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,
∴AE⊥BC,BE=CE=4cm,
在Rt△DEC中,CD==5cm,故①正确;
②∵∠ACD=∠CAD,
∴AD=CD=5cm,
∴AE=8cm,
在Rt△AEC中,AC==4cm,故②错误;
③∵∠DAF=∠BAE,∠AFD=∠AEB,
∴△DAF∽△BAE,
∴DF:AD=BE:AB,即DF:5=4:4,
解得DF=.
故DF=cm,故③错误;
④△ACD的面积为5×4÷2=10cm2,故④正确.
故选:B.
8.(2020?文成县二模)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A.4 B.6 C. D.
【解答】解:设AC=a,AB=b,BC=c,则a+b=8,c2=a2+b2,HG=c﹣b,DG=c﹣a,
则阴影部分的面积S=HG?DG=(c﹣b)(c﹣a)=2,
∵(a+b)2=a2+b2+2ab=64,
∴ab=32﹣,
∴S=c2﹣c(a+b)+ab=c2﹣8c+32﹣=2,
解得c1=6,c2=10(舍去).
故选:B.
9.(2020春?沛县期中)两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2﹣b2=c2 D.a2+b2=c2
【解答】解:根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:D.
10.(2020春?新乡期末)如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是( )
A.13 B. C.47 D.
【解答】解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:
x2=32+52=34;
y2=22+32=13;
z2=x2+y2=47;
即最大正方形E的面积为:z2=47,边长为z=.
故选:B.
11.(2019秋?崇川区期末)如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=16,则S1的值为( )
A.7 B.8 C.9 D.10
【解答】解:∵由勾股定理得:AC2+BC2=AB2,
∴S3+S2=S1,
∵S1+S2+S3=16,
∴2S1=16,
∴S1=8,
故选:B.
12.(2019秋?余杭区期末)如图,在Rt△ABC中,∠ACB=90°,以AB,AC,BC为边作等边△ABD,等边△ACE,等边△CBF.设△AEH的面积为S1,△ABC的面积为S2,△BFG的面积为S3,四边形DHCG的面积为S4,则下列结论正确的是( )
A.S2=S1+S3+S4 B.S1+S2=S3+S4
C.S1+S4=S2+S3 D.S1+S3=S2+S4
【解答】解:设AC=a,BC=b,AB=c,
∵△ABD,△ACE,△CBF都是等边三角形,
∴,,.
∵∠ACB=90°,
∴a2+b2=c2.
∴,
即S△ACE+S△BCF=S△ABD.
∴S1+S3=S2+S4.
故选:D.
13.(2019秋?偃师市期末)如图,在△ABC中,AB=AC=5,BC=6,P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
A.4.8 B.6 C.3.8 D.5
【解答】解:过A点作AF⊥BC于F,连结AP,如图.
∵△ABC中,AB=AC=5,BC=6,
∴BF=FC=BC=3,
∴△ABF中,AF===4.
∵S△ABC=S△ABP+S△ACP,
∴×6×4=×5×PD+×5×PE,
∴12=×5×(PD+PE),
PD+PE=4.8.
故选:A.
14.(2019秋?凤翔县期末)正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S2,…按此规律继续下去,则S5的值为( )
A. B. C. D.
【解答】解:在图中标上字母E,如图所示.
∵正方形ABCD的边长为1,△CDE为等腰直角三角形,
∴DE2+CE2=CD2,DE=CE,
∴S2+S2=S1.
观察,发现规律:S1=12=1,S2=S1=,S3=S2=,S4=S3=,…,
∴Sn=()n﹣1.
当n=5时,S5=()5﹣1=()4,
故选:A.
15.(2019秋?仁寿县期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
【解答】解:由勾股定理得,正方形F的面积=正方形A的面积+正方形B的面积=32+52=34,
同理,正方形G的面积=正方形C的面积+正方形D的面积=22+32=13,
∴正方形E的面积=正方形F的面积+正方形G的面积=47,
故选:D.
二.填空题(共10小题)
16.(2020春?济阳区期末)如图,△ABC中,∠B=70°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为 80°或140°或10° .
【解答】解:如图,有三种情形:
①当AC=AD时,∵△ABC中,∠B=70°,∠ACB=90°,
∴∠CAB=20°,
∵AC=AD,
∴∠ADC=∠DCA=(180°﹣∠CAB)=80°;
②当CD′=AD′时,
∵∠CAB=20°,
∴∠D′CA=∠CAB=20°,
∴∠AD′C=180°﹣20°﹣20°=140°.
③当AC=AD″时,则∠AD″C=∠ACD″,
∵∠CAB=20°,∠AD″C+∠ACD″=∠CAB,
∴∠AD″C=10°,
故答案为:80°或140°或10°.
17.(2020?哈尔滨模拟)在△ABC中,∠ACB=90°,∠A=40°,D为AB边上一点,若△ACD是等腰三角形,则∠BCD的度数为 20°或50° .
【解答】解:如图,
当AC=AD时,∠ACD=∠ADC=(180°﹣40°)=70°,
∴∠BCD=90°﹣∠ACD=20°.
当CD′=AD′时,∠D′CA=∠A=40°,
∴∠BCD′=90°﹣40°=50°,
故答案为20°或50°.
18.(2019秋?北流市期中)如图,在Rt△ABC中,∠ACB=90°,∠BAC=40°,∠ACB的平分线与∠ABC的外角平分线交于点E,连接AE,则∠AEB的度数为 45° .
【解答】解:作EF⊥AC交CA的延长线于F,EG⊥AB于G,EH⊥BC交CB的延长线于H,
∵CE平分∠ACB,BE平分∠ABD,
∴EF=EH,EG=EH,
∴EF=EF,又EF⊥AC,EG⊥AB,
∴AE平分∠FAG,
∵∠CAB=40°,
∴∠BAF=140°,
∴∠EAB=70°,
∵∠ACB=90°,∠CAB=40°,
∴∠ABC=50°,
∴∠ABH=130°,又BE平分∠ABD,
∴∠ABE=65°,
∴∠AEB=180°﹣∠EAB﹣∠ABE=45°,
故答案为:45°.
19.(2019秋?潮阳区校级月考)如图,在△ABC中,∠ACB=90°,将∠A折叠,使点A落在边CB上的点A′处,折痕为CD;若∠A′DC=84°,则∠B= 39 °.
【解答】解:∵△CDA′与△CDA关于CD成轴对称,
∴∠ADC=∠A′DC=84°,
∵∠ACB=90°,
∴∠DCA=∠DCB=45°,
∵∠CDA=∠B+∠DCB,
∴∠B=84°﹣45°=39°
故答案为:39.
20.(2020春?历下区期末)有一个三角形的两边长是9和12,要使这个三角形成为直角三角形,则第三条边长的平方是 225或63 .
【解答】解:当第三边是斜边时,第三边的长的平方是:92+122=225;
当第三边是直角边时,第三边长的平方是:122﹣92=63;
故答案是:225或63.
21.(2020春?历下区期末)等腰三角形的腰长为17,底长为16,则其底边上的高为 15 .
【解答】解:如图:
AB=AC=17,BC=16.
△ABC中,AB=AC,AD⊥BC;
则BD=DC=BC=8;
Rt△ABD中,AB=17,BD=8;
由勾股定理,得:AD=.
故答案为:15.
22.(2019秋?滦州市期末)如图所示,∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,则BD的长为 20 .
【解答】解:∵∠ABC=90°,AC=13,BC=5,
∴AB==12,
又∵∠BAD=90°,AD=16,
∴BD==20,
故答案为:20.
23.(2020春?齐齐哈尔期末)如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1=;再过P1作P1P2⊥OP1且P1P2=1,得OP2=;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此继续,得OP2019= 2 .
【解答】解:由勾股定理得:OP1=,OP2=;OP3=2;
OP4==;
依此类推可得OPn=,
∴OP2019==2.
故答案为:2.
24.(2020?成都模拟)如图所示,已知线段AC=1,经过点A作AB⊥AC,使AB=AC,连接BC,在BC上截取BE=AB,在CA上截取CD=CE,则的值是 .
【解答】解:设CD=a,则CE=a,
∵AC=1,AB=AC,
∴AB=,
∵BE=AB,
∴BE=,
∴BC=a+,
在Rt△ABC中,AC2+BA2=BC2,
∴,
解得,a=﹣或a=﹣(舍去),
∴AD=1﹣a=,
∴=.
故答案为:.
25.(2019秋?青羊区期末)如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5= 5 .(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)
【解答】解:如图,连接MQ,作MG⊥EC于G,设PC交BM于TMN交EC于Q.
∵∠ABM=∠CBQ=90°,
∴∠ABC=∠MBQ,
∵BA=BM,BC=BQ,
∴△ABC≌△MBQ(SAS),
∴∠ACB=∠BQM=90°,
∵∠PQB=90°,
∴M,P,Q共线,
∵四边形CGMP是矩形,
∴MG=PC=BC,
∵∠BCT=∠MGQ=90°,∠BTC+∠CBT=90°,∠BQM+∠CBT=90°,
∴∠MQG=∠BTC,
∴△MGQ≌△BCT(AAS),
∴MQ=BT,
∵MN=BM,
∴NQ=MT,
∵∠MQG=∠BTC,
∴∠NQE=∠MTP,
∵∠E=∠MPT=90°,
则△NQE≌MTP(AAS),
∴S1+S5=S3=5.
故答案为:5.
三.解答题(共11小题)
26.(2019秋?南岸区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
【解答】解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=36°,
∴∠ABC=90°﹣∠A=54°,
∴∠CBD=126°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=63°;
(2)∵∠ACB=90°,∠CBE=63°,
∴∠CEB=90°﹣63°=27°.
又∵∠F=27°,
∴∠F=∠CEB=27°,
∴DF∥BE
27.(2019秋?雅安期末)如图,直线m∥n,△ABC的顶点B、C分别在直线n、m上,且∠ACB=90°,若∠1=50°.
求∠2的度数.
【解答】解:∵m∥n
∴∠ECB=∠1=50°,
又∵∠ACB=∠BCE+∠ACE=90°,
∴∠ACE=40°,
又∵∠ACE+∠2=180°
∴∠2=140°.
28.(2019秋?辛集市期末)如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.
(1)求∠ACE的度数.
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
【解答】解:(1)∵△ABC中,∠A=30°,∠B=60°,
∴∠ACB=180°﹣30°﹣60°=90°,
又∵CF平分∠ACB,
∴∠ACE=∠ACB=45°;
(2)∵CD⊥AB,∠B=60°,
∴∠BCD=90°﹣60°=30°,
又∵∠BCE=∠ACE=45°,
∴∠DCF=∠BCE﹣∠BCD=15°,
又∵∠CDF=75°,
∴∠CFD=180°﹣75°﹣15°=90°,
∴△CFD是直角三角形.
29.(2020春?莱州市期末)如图,△ABC≌△DBE,∠CBE=60°,∠DCB=30°.求证:DC2+BE2=AC2.
【解答】证明:∵△ABC≌△DBE,
∴BE=BC,AC=ED;
连接EC.则△BCE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
在Rt△DCE中,
DC2+CE2=DE2,
∴DC2+BE2=AC2.
30.(2019秋?大连期末)如图,在△ABC中,∠B=90,∠C=30°,AB=6cm,BC=6cm,动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以cm/s的速度移动,动点P、Q同时出发,到点C运动结束.设运动过程中△BPQ的面积为y(cm2),运动时间为t(s).
(1)点P运动到点A,t= 2 (s);
(2)请你用含t的式子表示y.
【解答】解:(1)点P运动到点A,t=6÷3=2(s);
故答案为:2.
(2)当0<t<2时,y=S△BPQ=?BQ?BP=?3t?t=t2,
即y=t2;
当t≥2时,作PH⊥BC于H,如图所示:
y=S△BPQ=?BQ?HP=×t×(18﹣3t)=﹣t2+t,
即y=﹣t2+t.
31.(2019秋?北碚区期末)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
【解答】(1)解:(1)BQ=2×2=4cm,
BP=AB﹣AP=8﹣2×1=6cm,
∵∠B=90°,
PQ===2(cm);
(2)解:根据题意得:BQ=BP,
即2t=8﹣t,
解得:t=;
即出发时间为秒时,△PQB是等腰三角形;
(3)解:分三种情况:
①当CQ=BQ时,如图1所示:
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
过B点作BE⊥AC于点E,
则BE===4.8(cm)
∴CE==3.6cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.
32.(2020春?越城区期中)如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.
(1)求AD的长;
(2)当△PDC的面积为15平方厘米时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得S△PMD=S△ABC?若存在,请求出t的值;若不存在,请说明理由.
【解答】解:(1)∵AB=AC=13,AD⊥BC,
∴BD=CD=5cm,且∠ADB=90°,
∴AD2=AC2﹣CD2
∴AD=12cm.
(2)AP=t,PD=12﹣t,
又∵由△PDM面积为PD×DC=15,
解得PD=6,∴t=6.
(3)假设存在t,
使得S△PMD=S△ABC.
①若点M在线段CD上,
即 时,PD=12﹣t,DM=5﹣2t,
由S△PMD=S△ABC,
即 ,
2t2﹣29t+50=0
解得t1=12.5(舍去),t2=2.(2分)
②若点M在射线DB上,即 .
由S△PMD=S△ABC
得 ,
2t2﹣29t+70=0
解得 ,.(2分)
综上,存在t的值为2或 或 ,使得S△PMD=S△ABC.(1分)
33.(2019春?行唐县期末)勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b﹣a
S四边形ADCB=S△ADC+S△ABC=﹣b2+ab
S四边形ADCB=S△ADB+S△BCD=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明
如图(2)中∠DAB=90°,求证:a2+b2=c2
【解答】证明:连结BD,过点B作DE边上的高BF,则BF=b﹣a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b﹣a),
∴ab+b2+ab=ab+c2+a(b﹣a),
∴a2+b2=c2.
34.(2019春?沙坪坝区校级月考)如图①,在Rt△ABC中∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)根据勾股定理的知识,请直接写出a,b,c之间的数量关系;
(2)若正方形EFMN的面积为64,Rt△ABC的周长为18,求Rt△ABC的面积.
【解答】解:(1)由勾股定理得,a2+b2=c2;
(2)∵正方形EFMN的面积为64,
∴c2=64,即c=8,
∵Rt△ABC的周长为18,
∴a+b+c=18,
∴a+b=10,
则Rt△ABC的面积=ab
=[(a+b)2﹣(a2+b2)]
=9.
35.(2019秋?陇西县期中)分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=()2+1=2 S1=;
OA32=()2+1=3 S2=;
OA42=()2+1=4 S3=…
(1)请用含有n(n为正整数)的式子表示Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
【解答】解:(1)+1=n+1
Sn=(n是正整数);
故答案是:;
(2)∵OA12=1,
OA22=()2+1=2,
OA32=()2+1=3,
OA42=()2+1=4,
∴OA12=,
OA2=,
OA3=,…
∴OA10=;
故答案是:;
(3)S12+S22+S32+…+S102
=()2+()2+()2+…+()2
=(1+2+3+…+10)
=.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
