浙教版九年级上册数学 第三章圆的基本性质测试卷(word版,含答案)
文档属性
| 名称 | 浙教版九年级上册数学 第三章圆的基本性质测试卷(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 16:39:52 | ||
图片预览


文档简介
九年级上册数学·第三章测试卷
九年级上册数学
第三章测试卷
一、选择题(每题3分,共30分)
1.下列说法正确的是?(
)
A.圆周角的度数等于所对弧的度数
B.圆是中心对称图形,也是轴对称图形
C.平分弦的直径垂直于弦
D.劣弧是大于半圆的弧
2.如图,已知AB和CD是⊙O的两条直径,连结AD,BC,则α和β的关系是(
)
A.α=β
B.β>2α
C.β<2α
D.β=2α
3.同圆中两条弦长为10和12,它们的弦心距为m和n,则(
)
A.m>n
B.m<n
C.
D.m、n的大小无法确定
4.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是(
)
A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B
5.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=(
)
A.54°
B.64°
C.27°
D.37°
6.已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆周角的度数为( )
A.
B.
C.90°或27°
D.45°或135°
7.如图,在半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为(
)
A.cm2
B.cm2
C.cm2
D.
1
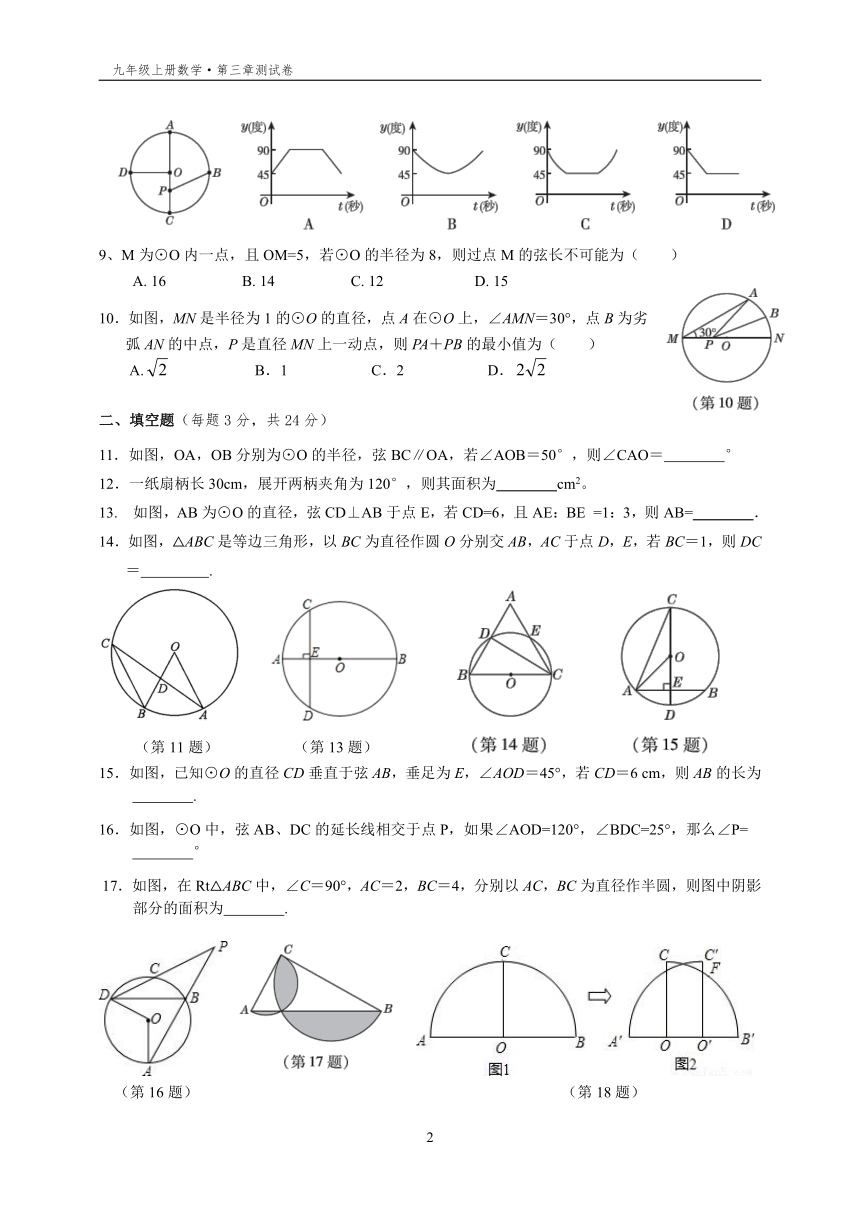
cm2
8.如图,已知点A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿OC——DO的路线做匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y(度)与t(秒)之间的函数关系最恰当的是(
)
9、M为⊙O内一点,且OM=5,若⊙O的半径为8,则过点M的弦长不可能为(
)
A.
16
B.
14
C.
12
D.
15
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为(
)
A.
B.1
C.2
D.
二、填空题(每题3分,共24分)
11.如图,OA,OB分别为⊙O的半径,弦BC∥OA,若∠AOB=50°,则∠CAO=
°?
12.一纸扇柄长30cm,展开两柄夹角为120°,则其面积为????????cm2。
13.
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE?=1:3,则AB=?????
??.
14.如图,△ABC是等边三角形,以BC为直径作圆O分别交AB,AC于点D,E,若BC=1,则DC=
.
如图,已知⊙O的直径CD垂直于弦AB,垂足为E,∠AOD=45°,若CD=6
cm,则AB的长为
.
16.如图,⊙O中,弦AB、DC的延长线相交于点P,如果∠AOD=120°,∠BDC=25°,那么∠P=
°
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,分别以AC,BC为直径作半圆,则图中阴影部分的面积为
.
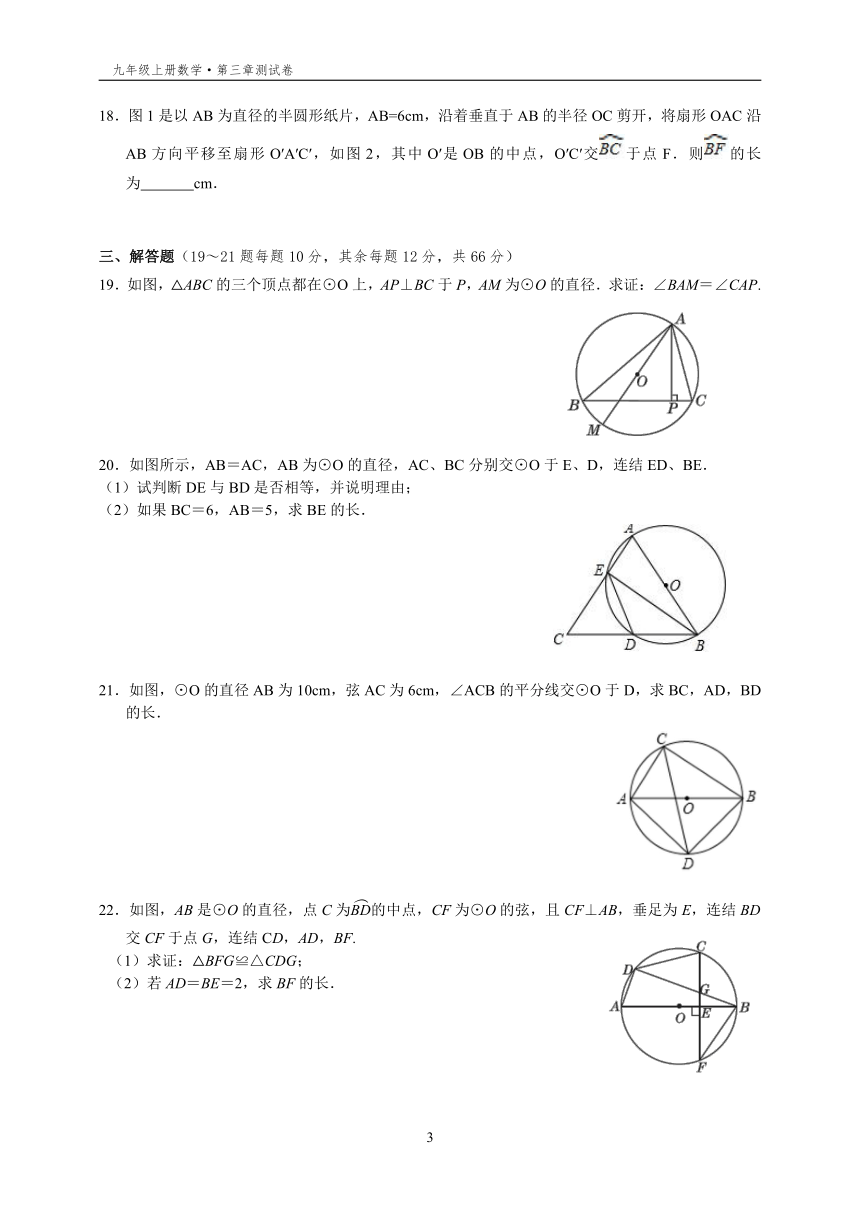
18.图1是以AB为直径的半圆形纸片,AB=6cm,沿着垂直于AB的半径OC剪开,将扇形OAC沿AB方向平移至扇形O′A′C′,如图2,其中O′是OB的中点,O′C′交于点F.则的长为??
??cm.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径.求证:∠BAM=∠CAP.
20.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
21.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连结BD交CF于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在矩形ABCD中,AD=2,以B为圆心,BC为半径画弧交AD于F.
(1)若的长为π,求圆心角∠CBF的度数;
(2)在(1)的条件下,求图中阴影部分的面积.(结果保留根号及π)
24.如图,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
参考答案
一、选择题
1.
B
2.
D
3.
A
4.
B
5.
C
D ∵弦AB把⊙O分成1:3两部分,
∴∠AOB=14×360°=90°,
∴∠ACB=12∠AOB=45°,
∵四边形ADBC是⊙O的内接四边形,
∴∠ADB=180°-∠ACB=135°.
∴这条弦所对的圆周角的度数是:45°或135°.
故选D.
7.A 点拨:∵扇形AOB的圆心角为90°,半径为2
cm,∴扇形AOB的面积为=π(cm2),两个半圆形的面积均为×π×12=(cm2).
如图,连结OD,BD,DA,
易知A,B,D三点共线.易得BD=OD=DA=
cm,且两个半圆形内的4个小弓形面积相等.
在半圆形OA中,S弓形AD=(S半圆形OA-S△OAD)=cm2,∴S阴影=S扇形AOB-S△AOB-2S弓形AD=π-×2×2-2×=-1
(cm2).
8.C 点拨:当动点P在OC上运动时,∠APB逐渐变小;当动点P在上运动时,∠APB不变;当动点P在DO上运动时,∠APB逐渐变大.
9.C
分析:过M的直径为16,即为最长的弦,最短的弦为垂直于直径OM的弦,利用垂径定理及勾股定理求出此时的弦长,即为最短的弦长,得到过M弦长的范围,即可得到正确的选项.
解答:解:过M作直径CD,由半径为8,得到CD=16,
过M作AB⊥CD,交圆0于点A、B,连接OA,
∴M为AB的中点,即AM=BM,
在Rt△AOM中,OA=8,OM=5,
根据勾股定理得:AM==,即AB=,
∴过M弦长的范围为2≤x≤16,
则过M的弦长不可能为12.
10.A
二、填空题
11.25°
12.300π?
13.
14.
15.3
cm
35°
根据圆周角定理,易求得∠ABD的度数;由于∠ABD是△PBD的外角,已知了∠BDP的度数,即可求出∠P的度数.
【解析】
∵∠AOD=120°
∴∠ABD=∠AOD=60°
∵∠ABD=∠BDC+∠P
∴∠P=∠ABD-∠BDC=60°-25°=35°.
17.π-4
18.π
分析:连接OF计算出圆心角,根据弧长公式计算即可.
解答:解:连接OF,
∵O′是OB的中点,OB′=OF,
∴OO′=OF,
∴∠OFO′=30°
∴∠FOO′=60°
∴==π.
点评:本题的关键是求出圆心角.
三、解答题
19.证明:连结BM.∵AP⊥BC,
∴∠CAP=90°-∠C.
∵AM为⊙O的直径,∴∠ABM=90°,
∴∠BAM=90°-∠M.
又∵∠M=∠C,
∴∠BAM=∠CAP.
20.(1)DE=BD;(2)4.8
【解析】
试题分析:(1)连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.
(2)由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC?BE=CB?AD.进而求出BE的长.
(1)如图,连接AD,则AD⊥BC,
在等腰三角形ABC中,AD⊥BC,
∴∠CAD=∠BAD(等腰三角形三线合一),
∴弧ED=弧BD,
∴DE=BD;
(2)∵AB=5,BD=BC=3,
∴AD=4,
∵AB=AC=5,
∴AC?BE=CB?AD,
∴BE=4.8.
考点:本题主要考查了等腰三角形的性质,圆周角定理
21.∵
AB是直径.
∴∠ACB=∠ADB=90°.???????????????
在Rt△ABC中,
BC=
(cm).
∵
CD平分∠ACB,
∴
.
∴
AD=BD.????????????????????????????
又在Rt△ABD中,
AD
2
+BD
2
=AB
2
,
∴
AD=BD=
AB=
×10=5
(cm).
根据直径所对的角是90°,判断出△ABC和△ABD是直角三角形,根据圆周角∠ACB的平分线交⊙O于D,判断出△ADB为等腰直角三角形,然后根据勾股定理求出具体值.
22.(1)证明:∵C是的中点,∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,∴CD=BF.
在△BFG和△CDG中,
∵
∴△BFG≌△CDG(AAS).
(2)解:连结OF,设⊙O的半径为r,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴BD2=AB2-AD2,即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,∴=,
∴BD=CF,易得EF=CE,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2.
23.解:(1)设∠CBF=n°,
∵的长为π,半径R=BC=AD=2,
∴=π,∴n=60,
即∠CBF的度数为60°.
(2)∵∠CBF=60°,且四边形ABCD为矩形,∴∠ABF=30°.
在Rt△ABF中,易得AF=BF=AD=1,
∴AB===.
易得S扇形CBF==π,
S矩形ABCD=AD·AB=2×=2
,
S△ABF=AF·AB=×1×=,∴S阴影=S矩形ABCD-(S扇形CBF+S△ABF)=2-=-π.
24.(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,
易得O为EF的中点,即OE=OF.
又∵OA=OB,
∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8
cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
(第5题)
(第7题)
(第11题)
(第13题)
(第16题)
(第18题)
九年级上册数学
第三章测试卷
一、选择题(每题3分,共30分)
1.下列说法正确的是?(
)
A.圆周角的度数等于所对弧的度数
B.圆是中心对称图形,也是轴对称图形
C.平分弦的直径垂直于弦
D.劣弧是大于半圆的弧
2.如图,已知AB和CD是⊙O的两条直径,连结AD,BC,则α和β的关系是(
)
A.α=β
B.β>2α
C.β<2α
D.β=2α
3.同圆中两条弦长为10和12,它们的弦心距为m和n,则(
)
A.m>n
B.m<n
C.
D.m、n的大小无法确定
4.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是(
)
A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B
5.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=(
)
A.54°
B.64°
C.27°
D.37°
6.已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆周角的度数为( )
A.
B.
C.90°或27°
D.45°或135°
7.如图,在半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为(
)
A.cm2
B.cm2
C.cm2
D.
1
cm2
8.如图,已知点A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿OC——DO的路线做匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y(度)与t(秒)之间的函数关系最恰当的是(
)
9、M为⊙O内一点,且OM=5,若⊙O的半径为8,则过点M的弦长不可能为(
)
A.
16
B.
14
C.
12
D.
15
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为(
)
A.
B.1
C.2
D.
二、填空题(每题3分,共24分)
11.如图,OA,OB分别为⊙O的半径,弦BC∥OA,若∠AOB=50°,则∠CAO=
°?
12.一纸扇柄长30cm,展开两柄夹角为120°,则其面积为????????cm2。
13.
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE?=1:3,则AB=?????
??.
14.如图,△ABC是等边三角形,以BC为直径作圆O分别交AB,AC于点D,E,若BC=1,则DC=
.
如图,已知⊙O的直径CD垂直于弦AB,垂足为E,∠AOD=45°,若CD=6
cm,则AB的长为
.
16.如图,⊙O中,弦AB、DC的延长线相交于点P,如果∠AOD=120°,∠BDC=25°,那么∠P=
°
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,分别以AC,BC为直径作半圆,则图中阴影部分的面积为
.
18.图1是以AB为直径的半圆形纸片,AB=6cm,沿着垂直于AB的半径OC剪开,将扇形OAC沿AB方向平移至扇形O′A′C′,如图2,其中O′是OB的中点,O′C′交于点F.则的长为??
??cm.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径.求证:∠BAM=∠CAP.
20.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
21.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连结BD交CF于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在矩形ABCD中,AD=2,以B为圆心,BC为半径画弧交AD于F.
(1)若的长为π,求圆心角∠CBF的度数;
(2)在(1)的条件下,求图中阴影部分的面积.(结果保留根号及π)
24.如图,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
参考答案
一、选择题
1.
B
2.
D
3.
A
4.
B
5.
C
D ∵弦AB把⊙O分成1:3两部分,
∴∠AOB=14×360°=90°,
∴∠ACB=12∠AOB=45°,
∵四边形ADBC是⊙O的内接四边形,
∴∠ADB=180°-∠ACB=135°.
∴这条弦所对的圆周角的度数是:45°或135°.
故选D.
7.A 点拨:∵扇形AOB的圆心角为90°,半径为2
cm,∴扇形AOB的面积为=π(cm2),两个半圆形的面积均为×π×12=(cm2).
如图,连结OD,BD,DA,
易知A,B,D三点共线.易得BD=OD=DA=
cm,且两个半圆形内的4个小弓形面积相等.
在半圆形OA中,S弓形AD=(S半圆形OA-S△OAD)=cm2,∴S阴影=S扇形AOB-S△AOB-2S弓形AD=π-×2×2-2×=-1
(cm2).
8.C 点拨:当动点P在OC上运动时,∠APB逐渐变小;当动点P在上运动时,∠APB不变;当动点P在DO上运动时,∠APB逐渐变大.
9.C
分析:过M的直径为16,即为最长的弦,最短的弦为垂直于直径OM的弦,利用垂径定理及勾股定理求出此时的弦长,即为最短的弦长,得到过M弦长的范围,即可得到正确的选项.
解答:解:过M作直径CD,由半径为8,得到CD=16,
过M作AB⊥CD,交圆0于点A、B,连接OA,
∴M为AB的中点,即AM=BM,
在Rt△AOM中,OA=8,OM=5,
根据勾股定理得:AM==,即AB=,
∴过M弦长的范围为2≤x≤16,
则过M的弦长不可能为12.
10.A
二、填空题
11.25°
12.300π?
13.
14.
15.3
cm
35°
根据圆周角定理,易求得∠ABD的度数;由于∠ABD是△PBD的外角,已知了∠BDP的度数,即可求出∠P的度数.
【解析】
∵∠AOD=120°
∴∠ABD=∠AOD=60°
∵∠ABD=∠BDC+∠P
∴∠P=∠ABD-∠BDC=60°-25°=35°.
17.π-4
18.π
分析:连接OF计算出圆心角,根据弧长公式计算即可.
解答:解:连接OF,
∵O′是OB的中点,OB′=OF,
∴OO′=OF,
∴∠OFO′=30°
∴∠FOO′=60°
∴==π.
点评:本题的关键是求出圆心角.
三、解答题
19.证明:连结BM.∵AP⊥BC,
∴∠CAP=90°-∠C.
∵AM为⊙O的直径,∴∠ABM=90°,
∴∠BAM=90°-∠M.
又∵∠M=∠C,
∴∠BAM=∠CAP.
20.(1)DE=BD;(2)4.8
【解析】
试题分析:(1)连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.
(2)由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC?BE=CB?AD.进而求出BE的长.
(1)如图,连接AD,则AD⊥BC,
在等腰三角形ABC中,AD⊥BC,
∴∠CAD=∠BAD(等腰三角形三线合一),
∴弧ED=弧BD,
∴DE=BD;
(2)∵AB=5,BD=BC=3,
∴AD=4,
∵AB=AC=5,
∴AC?BE=CB?AD,
∴BE=4.8.
考点:本题主要考查了等腰三角形的性质,圆周角定理
21.∵
AB是直径.
∴∠ACB=∠ADB=90°.???????????????
在Rt△ABC中,
BC=
(cm).
∵
CD平分∠ACB,
∴
.
∴
AD=BD.????????????????????????????
又在Rt△ABD中,
AD
2
+BD
2
=AB
2
,
∴
AD=BD=
AB=
×10=5
(cm).
根据直径所对的角是90°,判断出△ABC和△ABD是直角三角形,根据圆周角∠ACB的平分线交⊙O于D,判断出△ADB为等腰直角三角形,然后根据勾股定理求出具体值.
22.(1)证明:∵C是的中点,∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,∴CD=BF.
在△BFG和△CDG中,
∵
∴△BFG≌△CDG(AAS).
(2)解:连结OF,设⊙O的半径为r,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴BD2=AB2-AD2,即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,∴=,
∴BD=CF,易得EF=CE,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2.
23.解:(1)设∠CBF=n°,
∵的长为π,半径R=BC=AD=2,
∴=π,∴n=60,
即∠CBF的度数为60°.
(2)∵∠CBF=60°,且四边形ABCD为矩形,∴∠ABF=30°.
在Rt△ABF中,易得AF=BF=AD=1,
∴AB===.
易得S扇形CBF==π,
S矩形ABCD=AD·AB=2×=2
,
S△ABF=AF·AB=×1×=,∴S阴影=S矩形ABCD-(S扇形CBF+S△ABF)=2-=-π.
24.(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,
易得O为EF的中点,即OE=OF.
又∵OA=OB,
∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8
cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
(第5题)
(第7题)
(第11题)
(第13题)
(第16题)
(第18题)
同课章节目录
