2020年秋浙教版七年级数学上册第1章《有理数》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020年秋浙教版七年级数学上册第1章《有理数》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 142.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览



文档简介
2020年秋浙教版七年级数学上册第1章《有理数》单元测试卷
一、选择题(共8题;共24分)
1.-3相反数是(???
)
A.3?????
?B.-3?
?
C.????
?D.
2.若实数a的相反数是﹣2,则a等于(????
)
A.2???????B.﹣2???????C.????
?D.0
3.如图,数轴上被墨水遮盖的数可能为(???
)
A.1????????B.-1.5??????C.-3?????????D.-4.2
4.下列各数中,最小的数是(??
)
A.﹣3????B.0?????C.1????????D.2
5.﹣2的绝对值是(
??)
A.2????B.???????C.???????D.-2
6.
的结果是(???
)
A.?????B.2020?????C.?????D.-2020
7.实数a,b,c在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是(???
)
A.a??????B.b??????C.c??????D.无法确定
8.在数轴上表示数-1和2019的两点分别为点A和点B,则A、B两点之间的距离为(???
)
A.2018?????B.2019????C.2020?????D.2021
二、填空题(共8题;共24分)
9.如果用
表示温度升高3摄氏度,那么温度降低2摄氏度可表示为________.
10.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是;今有两数若其意义相反,则分别叫做正数与负数.若气温为零上
记作
,则
表示气温为________.
11.在实数-5,0,3中,最小的数是________.
12.已知a与b的和为2,b与c互为相反数,若
=1,则a=________.
13.绝对值大于
且小于
的所有整数的和是________。
14.
、
、
、
为互不相等的有理数,且
,
,则
________.
15.如图A,B,C,D,E分别是数轴上五个连续整数所对应的点,其中有一点是原点,数a对应的点在B与C之间,数b对应的点在D与E之间,若
则原点可能是________.
16.小康家里养了8头猪,质量分别为:104,98.5,96,91.8,102.5,100.7,103,95.5(单位:kg),每头猪超过100kg的千克数记作正数不足100kg的千克数记作负数,那么98.5对应的数记为________。
三、解答题(共7题;共52分)
17.把下面的有理数填入它所属于的集合的大括号内
-5.3,+5,20%,0,
,-7,-|-3|,-(-1.8)
正数集合{??????
?
}
整数集合{???????
}
分数集合{????
}
有理数集合{????
?
}
18.在数轴上表示下列各数:0,–4.5,
,–2,+7,
,并用“<”号连接起来.
19.某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位:元)
星期一
星期二
星期三
星期四
星期五
星期六
星期天
合计
-27.8
-70.3
200
138.1
-8
188
458
表中星期六的盈亏数被墨水涂污了,请你算出星期六的盈亏数,并说明星期六是盈还是亏?盈亏是多少
20.已知│a│=3,│b│=2,│c│=6,且a,b,c在数轴上的位置如图所示,求a+b+c的值.
21.某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超出或不足的部分分别用正数、负数来表示,记录如下表:若每袋标准质量为500g,则这批样品的总质量是多少?
与标准质量的差值(单位:g)
-3
-2
0
1
1.5
2.5
袋数(单位:袋)
1
4
3
4
5
3
22.已知a
,
b互为相反数,c与d互为倒数,m﹣1的绝对值是最小的正整数.
求:
﹣cd+m的值.
23.定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就点C是(A,B)的美好点例如:如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是〔A,B)的美好点,但点D是(B,A)的美好点。
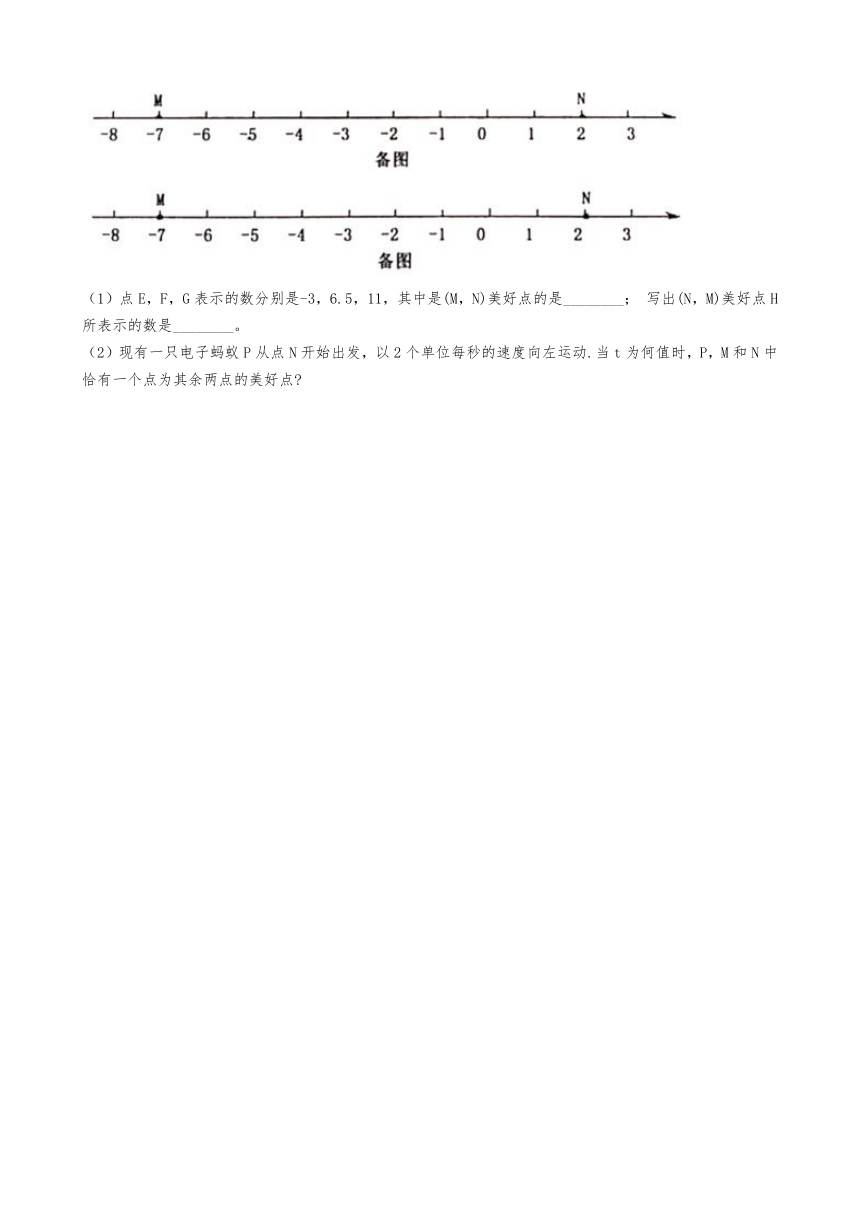
如图2,M,N为数轴上两点,点M所表示的数为-7,点N所表示的数为2.
(1)点E,F,G表示的数分别是-3,6.5,11,其中是(M,N)美好点的是________;
写出(N,M)美好点H所表示的数是________。
(2)现有一只电子蚂蚁P从点N开始出发,以2个单位每秒的速度向左运动.当t为何值时,P,M和N中恰有一个点为其余两点的美好点?
答案
一、选择题
1.解:
-3
的相反数是?3
故答案为:A.
2.解:∵2的相反数是﹣2,∴a=2
3.解:根据题意可知,墨水遮盖区域的数在-4和-2之间
∴数字可能为-3.
故答案为:C.
4.解:∵﹣3<0<1<2,
∴这四个数中最小的数是﹣3.
故答案为:A.
5.根据数轴上某个数与原点的距离叫做这个数的绝对值的定义,在数轴上,点﹣2到原点的距离是2,所以﹣2的绝对值是2,
故答案为:A.
6.解:
.
故答案为:B
7.解:观察有理数a,b,c在数轴上的对应点的位置可知,
这三个数中,实数a离原点最远,所以绝对值最大的是:a.
故答案为:A.
8.解:根据题意得:AB=|2019-(-1)|=|2019+1|=2020,
故答案为:C.
二、填空题
9.解:如果用+3℃表示温度升高3摄氏度,
那么温度降低2摄氏度可表示为:-2℃.
故答案为:-2℃.
10.解:若气温为零上10℃记作+10℃,则-3℃表示气温为零下3℃.
故答案为:零下3℃.
11.∵-5<0<3
故答案为:-5.
12.解:根据题意可知,a+b=2,b+c=0
∵|c|=1
∴c=1或-1
当c=1时,b=-1,此时a=3;
当c=-1时,b=1,此时a=1.
13.绝对值大于
且小于
的所有整数有:-11、-10、-9、-8、-7、-6、-5、-4、-3、-2、-1、0、1、2、3、4、5、6、7、8、9、10、11,
它们的和=0,
故填:0.
14.当
时,
∵
,即
,
∴
与
必互为相反数(否则
,不合题意),
∴
,
∴
,
,
∵
,即
,
∴
或
,
∴
(
不合题意,舍去),
,
∴
,
∴
当
时,
∵
,即
,
∴
与
必互为相反数(否则
,不合题意),
∴
,
∴
,
,
∵
,即
,
∴
或
,
∴
,
(
不合题意,舍去),
∴
,
∴
故答案为:6或2
15.解:当为A为原点时,|a|+|b|>3,
当B为原点时,|a|+|b|可能等于3,
当C为原点时,|a|+|b|<3,
当D为原点时,|a|+|b|<3,
当E为原点时,|a|+|b|可能等于3.
故答案为:B或E.
16.根据题意对应的数为-1.5
三、解答题
17.
解:正数集合{+5,20%,-(-1.8)···}
整数集合{+5,0,-7,-|-3|···}
分数集合{-5.3,20%,
,-(-1.8)···}
有理数集合{-5.3,+5,20%,0,
,-7,-|-3|···}
18.
解:如图所示:
用“<”号将它们连接起来为:
.
19.
解:
=
=
=458-420
=38
答:星期六是盈利,盈利38元。
20.
解:由数轴可知b<0,c>0,a>0,
∵│a│=3,│b│=2,│c│=6
∴a=3,b=-2,c=6
∴a+b+c=3+(-2)+6=7
21.
解:依题可得:
-3×1+(-2)×4+0×3+1×4+1.5×5+2.5×3,
=-3-8+0+4+7.5+7.5,
=8(g),
∵每袋标准质量为500g,
∴500×(1+4+3+4+5+3),
=500×20,
=10000(g),
∴10000+8=10008(g).
答:这批样品的总质量是10008g.
22.
解:∵a
,
b互为相反数,c
,
d互为倒数,
∴a+b=0,cd=1,
∵m﹣1的绝对值是最小的正整数,
∴m﹣1=﹣1或m﹣1=1,
解得m=0或m=2,
∴①当m=0时,原式=0﹣1+0=﹣1;
②当m=2时,原式=0﹣1+2=1.
23.
(1)G;-4或-16
(2)解:根据美好点的定义,P,M和N中恰有一个点为其余两点的美好点分6种情况,
第一情况:当P为【M,N】的美好点,点P在M,N之间,如图1,
当MP=2PN时,酬N=3,点P对应的数为2-3=-1,因此t=1.5秒;
第二种情况,当P为【N,M】的美好点,点P在M,N之间,如图2,
当2PM=PN时,NP=6,点P对应的数为2-6=-4,因此t=3秒
第三种情况,P为【N,M】的美好点,点P在M左侧,如图3,
当PN=2MN时,NP=18,点P对应的数为2-18=-16,因此t=9秒
第四种情况,M为【P,N】的美好点,点P在M左侧,如图4,
当M=2N时,NP=27,点P对应的数为2-27=-25,因此t=13.5秒
第五种情况,M为【N,P】的美好点,点P在M左侧,如图5,
当MN=2MP时,NP=135,点P对应的数为2-13.5=-1.5,因此t=6.75秒;
第六种情况,M为【N,P】的美好点,点P在M,N左侧,如图6,
当MN=时,NP=45,点P对应的数为2-4.5=-2.5,因此t=2.25秒;
综上所述,t的值为:1.5,2.25,3,6.75,9,13.5
一、选择题(共8题;共24分)
1.-3相反数是(???
)
A.3?????
?B.-3?
?
C.????
?D.
2.若实数a的相反数是﹣2,则a等于(????
)
A.2???????B.﹣2???????C.????
?D.0
3.如图,数轴上被墨水遮盖的数可能为(???
)
A.1????????B.-1.5??????C.-3?????????D.-4.2
4.下列各数中,最小的数是(??
)
A.﹣3????B.0?????C.1????????D.2
5.﹣2的绝对值是(
??)
A.2????B.???????C.???????D.-2
6.
的结果是(???
)
A.?????B.2020?????C.?????D.-2020
7.实数a,b,c在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是(???
)
A.a??????B.b??????C.c??????D.无法确定
8.在数轴上表示数-1和2019的两点分别为点A和点B,则A、B两点之间的距离为(???
)
A.2018?????B.2019????C.2020?????D.2021
二、填空题(共8题;共24分)
9.如果用
表示温度升高3摄氏度,那么温度降低2摄氏度可表示为________.
10.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是;今有两数若其意义相反,则分别叫做正数与负数.若气温为零上
记作
,则
表示气温为________.
11.在实数-5,0,3中,最小的数是________.
12.已知a与b的和为2,b与c互为相反数,若
=1,则a=________.
13.绝对值大于
且小于
的所有整数的和是________。
14.
、
、
、
为互不相等的有理数,且
,
,则
________.
15.如图A,B,C,D,E分别是数轴上五个连续整数所对应的点,其中有一点是原点,数a对应的点在B与C之间,数b对应的点在D与E之间,若
则原点可能是________.
16.小康家里养了8头猪,质量分别为:104,98.5,96,91.8,102.5,100.7,103,95.5(单位:kg),每头猪超过100kg的千克数记作正数不足100kg的千克数记作负数,那么98.5对应的数记为________。
三、解答题(共7题;共52分)
17.把下面的有理数填入它所属于的集合的大括号内
-5.3,+5,20%,0,
,-7,-|-3|,-(-1.8)
正数集合{??????
?
}
整数集合{???????
}
分数集合{????
}
有理数集合{????
?
}
18.在数轴上表示下列各数:0,–4.5,
,–2,+7,
,并用“<”号连接起来.
19.某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位:元)
星期一
星期二
星期三
星期四
星期五
星期六
星期天
合计
-27.8
-70.3
200
138.1
-8
188
458
表中星期六的盈亏数被墨水涂污了,请你算出星期六的盈亏数,并说明星期六是盈还是亏?盈亏是多少
20.已知│a│=3,│b│=2,│c│=6,且a,b,c在数轴上的位置如图所示,求a+b+c的值.
21.某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超出或不足的部分分别用正数、负数来表示,记录如下表:若每袋标准质量为500g,则这批样品的总质量是多少?
与标准质量的差值(单位:g)
-3
-2
0
1
1.5
2.5
袋数(单位:袋)
1
4
3
4
5
3
22.已知a
,
b互为相反数,c与d互为倒数,m﹣1的绝对值是最小的正整数.
求:
﹣cd+m的值.
23.定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就点C是(A,B)的美好点例如:如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是〔A,B)的美好点,但点D是(B,A)的美好点。
如图2,M,N为数轴上两点,点M所表示的数为-7,点N所表示的数为2.
(1)点E,F,G表示的数分别是-3,6.5,11,其中是(M,N)美好点的是________;
写出(N,M)美好点H所表示的数是________。
(2)现有一只电子蚂蚁P从点N开始出发,以2个单位每秒的速度向左运动.当t为何值时,P,M和N中恰有一个点为其余两点的美好点?
答案
一、选择题
1.解:
-3
的相反数是?3
故答案为:A.
2.解:∵2的相反数是﹣2,∴a=2
3.解:根据题意可知,墨水遮盖区域的数在-4和-2之间
∴数字可能为-3.
故答案为:C.
4.解:∵﹣3<0<1<2,
∴这四个数中最小的数是﹣3.
故答案为:A.
5.根据数轴上某个数与原点的距离叫做这个数的绝对值的定义,在数轴上,点﹣2到原点的距离是2,所以﹣2的绝对值是2,
故答案为:A.
6.解:
.
故答案为:B
7.解:观察有理数a,b,c在数轴上的对应点的位置可知,
这三个数中,实数a离原点最远,所以绝对值最大的是:a.
故答案为:A.
8.解:根据题意得:AB=|2019-(-1)|=|2019+1|=2020,
故答案为:C.
二、填空题
9.解:如果用+3℃表示温度升高3摄氏度,
那么温度降低2摄氏度可表示为:-2℃.
故答案为:-2℃.
10.解:若气温为零上10℃记作+10℃,则-3℃表示气温为零下3℃.
故答案为:零下3℃.
11.∵-5<0<3
故答案为:-5.
12.解:根据题意可知,a+b=2,b+c=0
∵|c|=1
∴c=1或-1
当c=1时,b=-1,此时a=3;
当c=-1时,b=1,此时a=1.
13.绝对值大于
且小于
的所有整数有:-11、-10、-9、-8、-7、-6、-5、-4、-3、-2、-1、0、1、2、3、4、5、6、7、8、9、10、11,
它们的和=0,
故填:0.
14.当
时,
∵
,即
,
∴
与
必互为相反数(否则
,不合题意),
∴
,
∴
,
,
∵
,即
,
∴
或
,
∴
(
不合题意,舍去),
,
∴
,
∴
当
时,
∵
,即
,
∴
与
必互为相反数(否则
,不合题意),
∴
,
∴
,
,
∵
,即
,
∴
或
,
∴
,
(
不合题意,舍去),
∴
,
∴
故答案为:6或2
15.解:当为A为原点时,|a|+|b|>3,
当B为原点时,|a|+|b|可能等于3,
当C为原点时,|a|+|b|<3,
当D为原点时,|a|+|b|<3,
当E为原点时,|a|+|b|可能等于3.
故答案为:B或E.
16.根据题意对应的数为-1.5
三、解答题
17.
解:正数集合{+5,20%,-(-1.8)···}
整数集合{+5,0,-7,-|-3|···}
分数集合{-5.3,20%,
,-(-1.8)···}
有理数集合{-5.3,+5,20%,0,
,-7,-|-3|···}
18.
解:如图所示:
用“<”号将它们连接起来为:
.
19.
解:
=
=
=458-420
=38
答:星期六是盈利,盈利38元。
20.
解:由数轴可知b<0,c>0,a>0,
∵│a│=3,│b│=2,│c│=6
∴a=3,b=-2,c=6
∴a+b+c=3+(-2)+6=7
21.
解:依题可得:
-3×1+(-2)×4+0×3+1×4+1.5×5+2.5×3,
=-3-8+0+4+7.5+7.5,
=8(g),
∵每袋标准质量为500g,
∴500×(1+4+3+4+5+3),
=500×20,
=10000(g),
∴10000+8=10008(g).
答:这批样品的总质量是10008g.
22.
解:∵a
,
b互为相反数,c
,
d互为倒数,
∴a+b=0,cd=1,
∵m﹣1的绝对值是最小的正整数,
∴m﹣1=﹣1或m﹣1=1,
解得m=0或m=2,
∴①当m=0时,原式=0﹣1+0=﹣1;
②当m=2时,原式=0﹣1+2=1.
23.
(1)G;-4或-16
(2)解:根据美好点的定义,P,M和N中恰有一个点为其余两点的美好点分6种情况,
第一情况:当P为【M,N】的美好点,点P在M,N之间,如图1,
当MP=2PN时,酬N=3,点P对应的数为2-3=-1,因此t=1.5秒;
第二种情况,当P为【N,M】的美好点,点P在M,N之间,如图2,
当2PM=PN时,NP=6,点P对应的数为2-6=-4,因此t=3秒
第三种情况,P为【N,M】的美好点,点P在M左侧,如图3,
当PN=2MN时,NP=18,点P对应的数为2-18=-16,因此t=9秒
第四种情况,M为【P,N】的美好点,点P在M左侧,如图4,
当M=2N时,NP=27,点P对应的数为2-27=-25,因此t=13.5秒
第五种情况,M为【N,P】的美好点,点P在M左侧,如图5,
当MN=2MP时,NP=135,点P对应的数为2-13.5=-1.5,因此t=6.75秒;
第六种情况,M为【N,P】的美好点,点P在M,N左侧,如图6,
当MN=时,NP=45,点P对应的数为2-4.5=-2.5,因此t=2.25秒;
综上所述,t的值为:1.5,2.25,3,6.75,9,13.5
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
