浙教版数学九年级上册第4章 相似三角形单元测试卷(含答案)
文档属性
| 名称 | 浙教版数学九年级上册第4章 相似三角形单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 11:51:06 | ||
图片预览


文档简介
第四章
相似三角形单元测试卷
一、填空题:(36分)
1、已知三个数2、4、8,请再添一个数,使它们构成一个比例式,则这个数可以是 .
2、已知=4,=9,是的比例中项,则= .
3、若,则 ;
4、在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________.
5、一本书的长与宽之比为黄金比,若它的长为20cm,则它的宽是 cm(保留根号).
6、如图1,在ΔABC中,DE∥BC,且AD∶BD=1∶2,则 .
(?http:?/??/?www.czsx.com.cn?)
图1
图2
图3
7、如图2,要使ΔABC∽ΔACD,需补充的条件是 .(只要写出一种)
8、.如图3,若两个多边形相似,则= .
9、一公园占地面积约为800000,若按比例尺1∶2000缩小后,其面积约为 .
10、如图4,点P是RtΔABC斜边AB上的任意一点(A、B两点除外)过点P作一条直线,使截得的三角形与RtΔABC相似,这样的直线可以作 条.
(?http:?/??/?www.czsx.com.cn?)
图4
图5
图6
11、如图5,四边形BDEF是RtΔABC的内接正方形,若AB=6,BC=4,则DE= .
12、如图6,ΔABC与ΔDEF是位似三角形,且AC=2DF,则OE∶OB= .
二、选择题:(30分)
13、下列各组数中,成比例的是( )
A.-6,-8,3,4 B.-7,-5,14,5 C.3,5,9,12 D.2,3,6,12
14、若,则k的值为(
)
A、2
B、-1
C、2或-1
D、不存在
15、如图7,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=(
)
A、
B、
C、
D、
(?http:?/??/?www.czsx.com.cn?)
图7
图8
图9
16、如图8,△ABC中,DE∥FG∥BC,且DE、FG将△ABC的面积三等分,若BC=12cm,则FG的长为(
)
A、8cm
B、6cm
C、cm
D、cm
17、下列说法中不正确的是( )
A.有一个角是30°的两个等腰三角形相似;B.有一个角是60°的两个等腰三角形相似;
C.有一个角是90°的两个等腰三角形相似;D.有一个角是120°的两个等腰三角形相似.
18、如图9,已知ΔABC和ΔABD都是⊙O的内接三角形,AC和BD相交于点E,则与ΔADE相似的三角形是( )
A.ΔBCE B.ΔABC C.ΔABD D.ΔABE
(?http:?/??/?www.czsx.com.cn?)
图10
图11
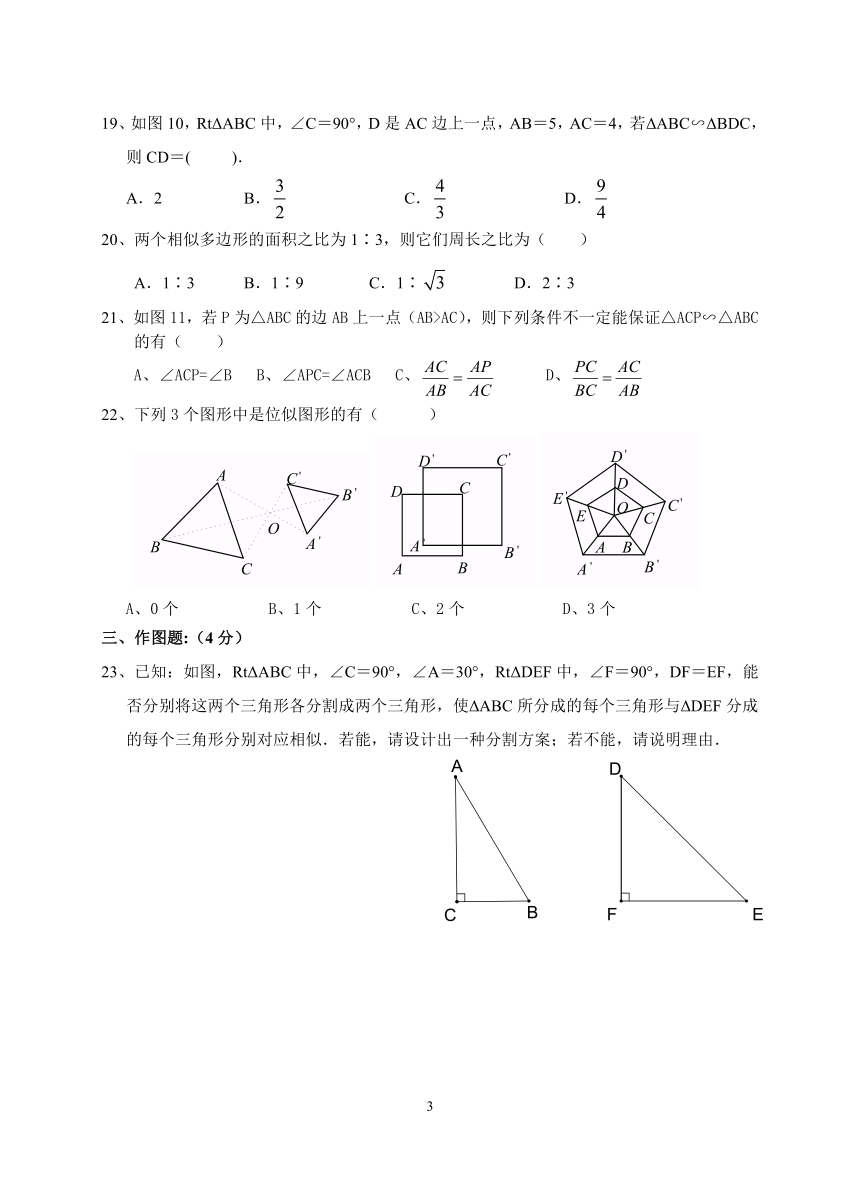
19、如图10,RtΔABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若ΔABC∽ΔBDC,
则CD=(
).
A.2 B. C. D.
20、两个相似多边形的面积之比为1∶3,则它们周长之比为( )
A.1∶3 B.1∶9 C.1∶ D.2∶3
21、如图11,若P为△ABC的边AB上一点(AB>AC),则下列条件不一定能保证△ACP∽△ABC的有(
)
A、∠ACP=∠B
B、∠APC=∠ACB
C、
D、
22、下列3个图形中是位似图形的有(
)
(?http:?/??/?www.czsx.com.cn?)
A、0个
B、1个
C、2个
D、3个
三、作图题:(4分)
23、已知:如图,RtΔABC中,∠C=90°,∠A=30°,RtΔDEF中,∠F=90°,DF=EF,能否分别将这两个三角形各分割成两个三角形,使ΔABC所分成的每个三角形与ΔDEF分成的每个三角形分别对应相似.若能,请设计出一种分割方案;若不能,请说明理由.
四、解答题(30分)
24、如图,已知AD、BE是△ABC的两条高,试说明AD·BC=BE·AC
25、如图判断4×4方格中的两个三角形是否相似,并说明理由.
26、如图所示,在离某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿垂直地面,
影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,那么这棵树高约有多少米?
27、如图所示,小华在晚上由路灯A走向路灯B,当他走到点P时,
发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,
发现他身前影子的顶部刚好接触到路灯B的底部,已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
?
(1)求两个路灯之间的距离;
?
(2)当小华走到路灯B时,他在路灯A下的影长是多少?
?
28、如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.
(?http:?/??/?www.czsx.com.cn?)
参考答案
填空题:
(1)、1或4或16;(2)、±6;(3)、-;(4)、1.6或2.5;(5)、;
(6)、1:8;(7)、∠ACD=∠B或∠ADC=∠ACB或AD:AC=AC:AB;(8)、31.5;
(9)、0.2;(10)、3;(11)、2.4;(12)、1:2
二、选择题:
13
14
15
16
17
18
19
20
21
22
A
C
A
C
A
A
D
C
D
C
三、作图题:
23、(略)
四、解答题:
24、证明:∵AD、BE是△ABC的高
∴∠ADC=∠BEC
∵∠C=∠C
∴△ADC∽△BEC
∴AD:BE=AC:BC
∴AD×BC=BE×AC
25、解:由图得,AB=,AC=2,BC=5,EF=,ED=2,DF=,
∴AB:EF=AC:ED=BC:DF=:
∴△ABC∽△DEF
26、解:过点C作CE∥AD交AB于点E,则CD=AE=2m,△BCE∽△B/BA/
∴A/
B/:B/B=BE:BC
即,1.2:2=
BE:4
∴BE=2.4
∴AB=2.4+2=4.4
答:这棵树高4.4m。
27、1.(1)18m.
(2)3.6m.
28、解:(1)若点A,P,D分别与点B,C,P对应,即△APD∽△BCP,
∴
HYPERLINK
"http://www.czsx.com.cn"
,
∴?,
∴AP2-7AP+6=0,
∴AP=1或AP=6,
检测:当AP=1时,由BC=3,AD=2,BP=6,
∴,
又∵∠A=∠B=
90°,∴△APD∽△BCP.
?
当AP=6时,由BC=3,AD=2,BP=1,
又∵∠A=∠B=90°,
∴△APD∽△BCP.
?
(2)若点A,P,D分别与点B,P,C对应,即△APD∽△BPC.
∴
HYPERLINK
"http://www.czsx.com.cn"
,∴,
∴AP=.
?
检验:当AP=时,由BP=,AD=2,BC=3,
∴,
又∵∠A=∠B=90°,∴△APD∽△BPC.
?
因此,点P的位置有三处,即在线段AB距离点A1、、6
处.毛
姓
名
A
B
C
P
A
B
C
E
D
PAGE
1
相似三角形单元测试卷
一、填空题:(36分)
1、已知三个数2、4、8,请再添一个数,使它们构成一个比例式,则这个数可以是 .
2、已知=4,=9,是的比例中项,则= .
3、若,则 ;
4、在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________.
5、一本书的长与宽之比为黄金比,若它的长为20cm,则它的宽是 cm(保留根号).
6、如图1,在ΔABC中,DE∥BC,且AD∶BD=1∶2,则 .
(?http:?/??/?www.czsx.com.cn?)
图1
图2
图3
7、如图2,要使ΔABC∽ΔACD,需补充的条件是 .(只要写出一种)
8、.如图3,若两个多边形相似,则= .
9、一公园占地面积约为800000,若按比例尺1∶2000缩小后,其面积约为 .
10、如图4,点P是RtΔABC斜边AB上的任意一点(A、B两点除外)过点P作一条直线,使截得的三角形与RtΔABC相似,这样的直线可以作 条.
(?http:?/??/?www.czsx.com.cn?)
图4
图5
图6
11、如图5,四边形BDEF是RtΔABC的内接正方形,若AB=6,BC=4,则DE= .
12、如图6,ΔABC与ΔDEF是位似三角形,且AC=2DF,则OE∶OB= .
二、选择题:(30分)
13、下列各组数中,成比例的是( )
A.-6,-8,3,4 B.-7,-5,14,5 C.3,5,9,12 D.2,3,6,12
14、若,则k的值为(
)
A、2
B、-1
C、2或-1
D、不存在
15、如图7,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=(
)
A、
B、
C、
D、
(?http:?/??/?www.czsx.com.cn?)
图7
图8
图9
16、如图8,△ABC中,DE∥FG∥BC,且DE、FG将△ABC的面积三等分,若BC=12cm,则FG的长为(
)
A、8cm
B、6cm
C、cm
D、cm
17、下列说法中不正确的是( )
A.有一个角是30°的两个等腰三角形相似;B.有一个角是60°的两个等腰三角形相似;
C.有一个角是90°的两个等腰三角形相似;D.有一个角是120°的两个等腰三角形相似.
18、如图9,已知ΔABC和ΔABD都是⊙O的内接三角形,AC和BD相交于点E,则与ΔADE相似的三角形是( )
A.ΔBCE B.ΔABC C.ΔABD D.ΔABE
(?http:?/??/?www.czsx.com.cn?)
图10
图11
19、如图10,RtΔABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若ΔABC∽ΔBDC,
则CD=(
).
A.2 B. C. D.
20、两个相似多边形的面积之比为1∶3,则它们周长之比为( )
A.1∶3 B.1∶9 C.1∶ D.2∶3
21、如图11,若P为△ABC的边AB上一点(AB>AC),则下列条件不一定能保证△ACP∽△ABC的有(
)
A、∠ACP=∠B
B、∠APC=∠ACB
C、
D、
22、下列3个图形中是位似图形的有(
)
(?http:?/??/?www.czsx.com.cn?)
A、0个
B、1个
C、2个
D、3个
三、作图题:(4分)
23、已知:如图,RtΔABC中,∠C=90°,∠A=30°,RtΔDEF中,∠F=90°,DF=EF,能否分别将这两个三角形各分割成两个三角形,使ΔABC所分成的每个三角形与ΔDEF分成的每个三角形分别对应相似.若能,请设计出一种分割方案;若不能,请说明理由.
四、解答题(30分)
24、如图,已知AD、BE是△ABC的两条高,试说明AD·BC=BE·AC
25、如图判断4×4方格中的两个三角形是否相似,并说明理由.
26、如图所示,在离某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿垂直地面,
影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,那么这棵树高约有多少米?
27、如图所示,小华在晚上由路灯A走向路灯B,当他走到点P时,
发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,
发现他身前影子的顶部刚好接触到路灯B的底部,已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
?
(1)求两个路灯之间的距离;
?
(2)当小华走到路灯B时,他在路灯A下的影长是多少?
?
28、如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.
(?http:?/??/?www.czsx.com.cn?)
参考答案
填空题:
(1)、1或4或16;(2)、±6;(3)、-;(4)、1.6或2.5;(5)、;
(6)、1:8;(7)、∠ACD=∠B或∠ADC=∠ACB或AD:AC=AC:AB;(8)、31.5;
(9)、0.2;(10)、3;(11)、2.4;(12)、1:2
二、选择题:
13
14
15
16
17
18
19
20
21
22
A
C
A
C
A
A
D
C
D
C
三、作图题:
23、(略)
四、解答题:
24、证明:∵AD、BE是△ABC的高
∴∠ADC=∠BEC
∵∠C=∠C
∴△ADC∽△BEC
∴AD:BE=AC:BC
∴AD×BC=BE×AC
25、解:由图得,AB=,AC=2,BC=5,EF=,ED=2,DF=,
∴AB:EF=AC:ED=BC:DF=:
∴△ABC∽△DEF
26、解:过点C作CE∥AD交AB于点E,则CD=AE=2m,△BCE∽△B/BA/
∴A/
B/:B/B=BE:BC
即,1.2:2=
BE:4
∴BE=2.4
∴AB=2.4+2=4.4
答:这棵树高4.4m。
27、1.(1)18m.
(2)3.6m.
28、解:(1)若点A,P,D分别与点B,C,P对应,即△APD∽△BCP,
∴
HYPERLINK
"http://www.czsx.com.cn"
,
∴?,
∴AP2-7AP+6=0,
∴AP=1或AP=6,
检测:当AP=1时,由BC=3,AD=2,BP=6,
∴,
又∵∠A=∠B=
90°,∴△APD∽△BCP.
?
当AP=6时,由BC=3,AD=2,BP=1,
又∵∠A=∠B=90°,
∴△APD∽△BCP.
?
(2)若点A,P,D分别与点B,P,C对应,即△APD∽△BPC.
∴
HYPERLINK
"http://www.czsx.com.cn"
,∴,
∴AP=.
?
检验:当AP=时,由BP=,AD=2,BC=3,
∴,
又∵∠A=∠B=90°,∴△APD∽△BPC.
?
因此,点P的位置有三处,即在线段AB距离点A1、、6
处.毛
姓
名
A
B
C
P
A
B
C
E
D
PAGE
1
同课章节目录
